О численном методе для задачи стокса с граничными условиями Неймана в невыпуклой области

Многие математические модели природных процессов описываются краевыми задачами с помощью систем уравнений с частными производными, имеющие ту или иную особенность. Особенность решения таких систем в двумерной замкнутой области Q может быть связана с вырождением исходных данных или наличием входящих углов на границе области. Будем говорить, что краевая задача имеет сильную сингулярность, если ее решение не принадлежит пространству Соболева Wg(Q). Другими словами, интеграл Дирихле от ее решения расходится. В случае, когда решение принадлежит пространству Соболева W2(Q), но не принадлежит пространству Соболева W^(^) краевая задача называется задачей со слабой сингулярностью или просто с сингулярностью. Например, обобщенное решение краевой эллиптической задачи с граничными условиями Дирихле в двумерной области, содержащей входящий угол на границе, т.е. угол из диапазона ©, 2^], принадлежит лишь пространству W 1+^ ^e (Q), ft G [0.25,1), где e — произвольное положительное действительное число. Поэтому приближенное решение, полученное классическими методами

О численном методе для задачи Стокса с граничными условиями Неймана ... конечных разностей или конечных элементов, сходится к точному решению не быстрее чем со скоростью O(h ) [1] .

Для краевых задач с сингулярностью существуют различные численные подходы, основанные на выделении сингулярных компонент обобщенного решения и сгущения сетки к точке сингулярности (см., например, [2, 3] ). Эти методы существенно усложняют схему метода конечных элементов (МКЭ), что влияет на скорость вычислительного процесса и точность результата.

В [4] для эллиптических задач с граничными условиями Дирихле было предложено определять решение как R _\nu -обобщенное в весовых пространствах Соболева. Теоретические результаты, связанные со существованием, единственностью и дифференциальными свойствами R _\nu -обобщенного решения различных задач изучены в [5 –9] . На основе этого подхода были созданы численные методы, позволяющие получать преимущество по порядку относительно шага сетки над классическими подходами (см., например, [10 –12] ).

В представленной работе рассмотрим задачу Стокса с граничными условиями Неймана, определим R _\nu -обобщенное решение задачи в весовых множествах. Теоретический анализ обобщенного решения задачи Стокса (Навье—Стокса) с граничными условиями Неймана выполнен в работах [13 –16] . В [13] изучена регулярность решения задачи в пространствах Соболева, существование и единственность слабых решений Навье—Стокса. В [14] показано как свойства оператора Стокса приводят к локальным или глобальным решениям для малых начальных данных. В [15] проведено теоретическое исследование решения нестационарной задачи, которая является линеаризацией модельной задачи со свободной границей. Доказаны оценки решения в нормах пространств Лебега и получено преимущество по сравнению со случаем граничного условия без проскальзывания. В [16] определяется связь свойств оператора Стокса—Неймана с оператором Стокса—Дирихле, в частности, связь их собственных значений. Здесь предложим численный метод решения задачи, основанный на определении R _\nu -обобщенного решения и введении в базис весовой функции в некоторых степенях. Проведен ряд численных экспериментов задачи в невыпуклой области. Экспериментально получим, что порядок сходимости приближенного решения к точному решению задачи не зависит от величины входящего угла.

Статья организована следующим образом. Раздел 1 содержит необходимые обозначения, определения пространств и множеств. Раздел 2 посвящен определению классического и R _\nu -обобщенного решений задачи Стокса с граничными условиями Неймана. В разделе 3 построена схема весового метода конечных элементов. В разделе 4 представлены результаты численных экспериментов и определены области выбора свободных параметров подхода. В заключении приведены выводы и намечены направления дальнейших исследований.

1.    Необходимые обозначения. Определения пространств и множеств

Область Q есть невыпуклый многоугольник с границей Г, содержащий входящий угол на границе в двумерном евклидовом пространстве ^ 2 , где х = (x i ,X 2 ) его элемент, dx = dx i dx 2 его мера и ||х|| = ( x 2 + x 2 ) 1/² его норма. Пусть вершина входящего угла совпадает с началом координат О = (0, 0). Вершину входящего угла будем называть точкой сингулярности. Пусть Q = Q U Г — замыкание области Q.

Введем необходимые обозначения. Пусть заданы векторные поля а = (- 1 ,- 2 ), с = (c i , С 2 ), d = (d i , d 2 ) и скалярное поле b, тогда

.      ( д2-1 д 2a1 д2-2 д 2a2 )T оператор Лапласа поля \bfa,

^\bfa               \partialx ²₁             \partialx ² ₂ ^, \partialx ²₁             \partialx ² ₂

div a = 01-+ + ^02 — дивергенция поля a , Vb = f-|—, -^ — градиент поля b.

\partialx 1            \partialx 2                                                                                                               \partialx 1 \partialx 2

Кроме того,

2 \partialb a•vb = \' 8Xi’ i=1

Va : Vc = £ i,j=1

Va : (cVb) = £ i,j=1

\partiala i _c \partialb \partialx j ^{c i} \partialx j ^,

\partiala i \partialc i

\partialx j \partialx j ^,

[a ( d • Vb)j : c = £ a j (di i,j=1

aVb : cVb = i,j=1

\partialb dxp cj ’ (Va d:

\partialb \partialb

^a i        ^c i        ^,

\partialx j \partialx j

c =E ^d i c j -

i,j=1

Через Q ^ обозначим область, образованную пересечением круга с центром в начале координат О и радиусом 5 с Q, т.е. Q ^ = { х G Q : ||х || <  6 ^ 1,5 > 0 } . Определим функцию р( х ) в Q, которую назовем весовой, имеющую следующий вид:

| х | , если х G Q i , р( х ) = <

I 5 , если х G Q \ Q i .

Определим необходимые нам весовые пространства и множества обобщенных функций.

Через L 2,_a (Q) обозначим весовое пространство функций v( х ) с ограниченной нормой

1Ык,_а (Q) = (У Р 2^{а (х) v 2 (х) d х} ) / .                               ⁽¹⁾

Причем, если а = 0, то L 2,o (Q) = L 2 (Q). Обозначим через W 1_{O I} (Q) пространство функций v( х ) таких, что v( х ) G W 1 _a (Q), если ограничена интегральная норма

Миъ . (щ =(ML . (_О> + £ iHD l -мн^ ) ¹/² , |l|=1

где D l -( х ) = :^^ — l-я обобщенная производная функции -( х ) : |l| = l i + I 2 , li — неотрицательные целые числа, i = 1, 2.

Введем следующие условия для функции -( х ):

| -( х ) | <  C i 5 ^{a т}р^т " ( х ), х G Q i ,

|D1v(х)| < Ci5" трт " 1(х), х G Qi, р2"(х)-2(х)dх > (C2)2 > 0,

\Omega\setminus\Omega\delta где C1 — положительная константа, \tau — малый положительный параметр, независящий от 5, а и -(х). Далее определим множества в введенных весовых пространствах. Через

L2,a(Q,5) обозначим множество функций v(x) из пространства L2,a(Q), удовлетворяющих условиям (3) и (5) с ограниченной нормой (1). Определим множество L0a(Q,5) функций v(x) таких, что v(x) g L0 ^(^, 5), если v(x) G L2,a(Q, 5) и f ра(x)v(x)dx = 0 с ограниченной ,\Omega нормой (1). Если а = 0, то L^ := L^ o(Q, 5). Через W21a(Q, 5) обозначим множество функций v(x) из весового пространства W21 а(Q), удовлетворяющих условиям (3)-(5) с ограниченной нормой (2). Если а = 0, то W1 := W1 0(Q, 5).

Для векторных полей, пространства и множества будем выделять жирным шрифтом, например, v = (v i ,V 2 ) : v G L2 ,_a (Q, 5), если V i G L 2 ,_a (Q,5),i = 1, 2, с ограниченной нормой 2                  1/2

IMUot = (e 1^^.(ч1 •

2.    Определение классического и R\nu-обобщенного решений задачи Стокса с граничными условиями Неймана.Связь R\nu-обобщенного и обобщенного решений

Задача Стокса с граничными условиями Неймана состоит в том, что, зная функции f = (f i ,f 2 ) в Q и г на Г необходимо найти поля скоростей u = (u i ,U 2 ) и давления р, которые удовлетворяют системе дифференциальных уравнений и граничных условий:

— △ u + V p = f	в     Q,
div u = 0	в     Q,
V V u + ( V u )T — p^ n = г	на     Г,

где n = (n i ,n 2 ) единичный вектор внешней нормали к Г.

Определим билинейные и линейную формы:

a( w , v

)=

V w : V (p ^2v v )d x ,

\Omega

b 1 ( w ,q) = — ^ q div (p ^2v w )d x , \Omega

b 2 ( w , q) = — У (p ^2v q) div w d x , \Omega

\Omega где ds — дифференциал по Г.

Пусть

l( v ) = У f ' (^ v )d x + У г • (p ^2v v )d s ,

\Gamma

f G L 2 ,/з (Q), г G L 2 ,, (Г), 0 <  ^ <  v.

Введем понятие R \nu -обобщенного решения задачи Стокса (6) – (8) с граничными условиями Неймана в весовых множествах.

Определение 1 (R _v -обобщенного решения). Пару функций ( u _v ,p _v ) G W 1 _v (Q, 5) x L 0 v (Q, 5) назовем R _v -обобщенным решением задачи Стокса (6) - (8) , если для всех пар функций ( v ,q) G W ¹ ,v (Q,5) x L 0 _v (Q, 5) справедливы интегральные тождества:

a( u v , v ) + b i ( v ,p v ) = l( v ),

b 2 ( u v ,q) = 0,

где f и г удовлетворяют условиям (11) и U " = (u i," ,U 2," ).

Определим связь между R _\nu -обобщенным и обобщенным решениями задачи Стокса (6) – (8) .

Во-первых, по аналогии с Леммой 4 [17] имеет место следующее утверждение: z \in W 1 " (^j 5) тогда и только тогда, когда p " z G W2 . По определению нормы (1) : q G L 0 " (Q, 5) тогда и только тогда, когда \rho ^\nu q \in L ⁰ ₂ .

Во-вторых, справедливы следующие представления для v = (v i ,V 2 ) и w = (w i ,W 2 ):

^{d (} p ²" v i )     „д⁽p " v i ) ₍ „ , dp "

—Т = p— +

\partialxj                               \partialxj                                      \partialxj

Согласно этому, билинейная форма a(w, v) в (9) может быть представлена в следующем виде:

a(w, v) = a(w, v) + a1(w, v), где

a(w,v) = У V(p"w) : V(p"v)dx,

\Omega a1(w, v) = У ^V(p"w) : (vVp") — (wVp") : V(p"v) — (wVp") : (vVp")]dx.

\Omega\delta

Билинейные формы bi(w,q) и b2(w, q) в (8)

могут быть представлены в таком виде:

^bi^(w,q) = b^(w,q⁾ + ^d(w,q)

и     b2(w, q) = b(w, q) - d(w, q), где

b^(w,q⁾ = ^— У ⁽p"q) ^{div (}p"^w)dx, \Omega

^d(w, q) = ^- У ⁽p" q^)(w • ^Vp"^)dx. \Omega\delta

Кроме того,

r

l(v) = / f • vdx +

\Omega

У Г • V ds = l(v),

\Gamma

где f = p"f, Г = p"г и v = p"v.

На основании вышеизложенного, определим обобщенное решение задачи (6)–(8).

Определение 2 (обобщенного решения). Пару функций (U,p) G W1 x L0 назовем обобщенным решением задачи Стокса (6)-(8), если для всех пар функций (v, 7) G W1 x L0 справедливы интегральные тождества:

a(U, v) + b(v,p) = l(v),

b(U,q) = 0, где U = (ui, U2).

Замечание 1. Вариационная постановка задачи (12), (13) при определении R_\nu -обобщенного решения задачи (6)–(8), в отличие от вариационной задачи (14), (15) при определении обобщенного решения задачи (6)–(8), является несимметричной ввиду наличия формы dp, •), определенной в 5-окрестности точки сингулярности.

Замечание 2. Отличие определения решений имеет место в \delta-окрестности входящего угла.

Замечание 3. Покажем, что приближенное решение, полученное на основании определенного R\nu-обобщенного решения имеет порядок сходимости к точному решению задачи, независящий от величины входящего угла, в отличие от приближенного обобщенного решения, порядок сходимости которого уменьшается с увеличением величины входящего угла. Результат достигается благодаря качественному учету погрешности в Q^. При этом погрешность не распространяется из Q^ во внутреннюю часть расчетной области. Результат достигается без сгущения сетки к точке сингулярности.

3.    Схема весового метода конечных элементов

Построим схему весового метода конечных элементов для задачи Стокса (6)–(8), основанную на определении R_\nu-обобщенного решения. Для этой цели проведем квазиравномерную триангуляцию Th области Q [1]. Пусть Ls — произвольный треугольник триангуляции со стороной порядка h, его назовем конечным элементом. Обозначим через Qh = U_{L eT}h Ls объединение всех конечных элементов. Для компонент вектора скоростей, в качестве узлов аппроксимации, будем использовать вершины и середины сторон Ls . Их множество обозначим через R^vel, а для скалярной функции давления вершины конечных элементов. Их множество обозначим через R^presи определим конечно-элементную пару Тейлора—Худа 2-го порядка (см., например, [18]) Xh х Zh, где Xh = Xh х Xh и

Xh = {v^hG C(Q) : v^h|Ls G P2(Ls) ' L G Th}; Zh = {z^hG C(Q) : zh^ G P-(Ls) ^L_s G Th}.

На основании вышеизложенного, представим особые базисные функции и построим схему весового МКЭ для приближенного решения задачи Стокса (6)–(8). Каждому узлу Nk \in R^vel и Ml \in R^pres соответствует базисная функция

0k (x) = p—* (x)pk (x) и Xl (x) = p-* (x)^k (x),     k, l = 0,1,..., где pk(x) G Xh, Pk(Ni) = ^ki и ^i(x) G Zh, ^i(Mi) = Su, i,k,l = 0,1,..., Sj — символ Кронекера, \nu\ast и \mu\ast свободные (положительные) параметры подхода.

Через Vh и Qh обозначим множества для компонент вектора скоростей и функции давления как линейные оболочки систем базисных функций \{\thetak\}k и \{\chil\}l соответственно uh,i(x) = ^d^k 0k (x),     uhp(x) = ^d2k+i0k (x),     ph(x) = £eiXi(x),       (16)

kk  l где dj = ph* (N[j/2])dj, ei = p^* (Mi)ei. Коэффициенты dj и ei в (16) определяются как решение системы линейных алгебраических уравнений (см. (19)) ниже. Пусть Vh = Vh х Vh и Vh С W1^(Qh,S) и Qh С 1%и(Qh,S)

Введем понятие приближенного R\nu-обобщенного решения задачи Стокса (6)–(8).

Определение 3. Приближенным R_\nu-обобщенным решением задачи Стокса (6)–(8) по весовому методу конечных элементов назовем пару функций (uh, ph) G Vh \times Q_h такую, что для произвольной пары функций (v^h, q^h) G Vh х Qh справедливы интегральные тождества:

a(uh, v^h)+ bi(v^h,ph)= l(v^h),                                 (17)

b2(u^hh,q^h )=0,                                                 (18)

где f и г удовлетворяют условиям (11) и uh = (u^h_h,uh_h )•

Задача (17), (18) порождает систему линейных алгебраических уравнений

I Г-Ц d-1FL            .....

где у — dd^d,^,.,.., ,d, ,d3,d,,...) , z — (eo ,61,62,...) , F — вектор-столбец значений линейной формы l(6k).

Итерационный процесс с переобуславливанием матрицы системы вида (19) построен и реализован (см., например, [11]). В следующем параграфе проведем необходимые численные эксперименты и покажем преимущество предложенного нами весового МКЭ.

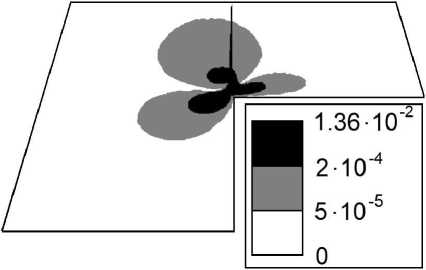
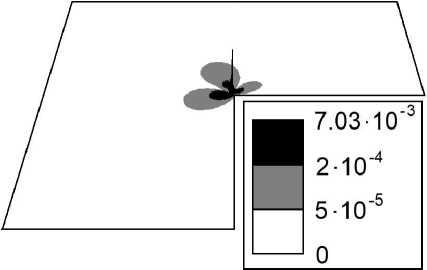
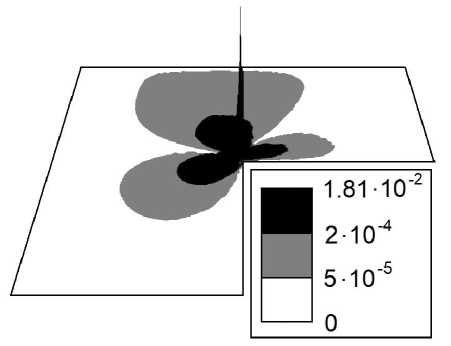
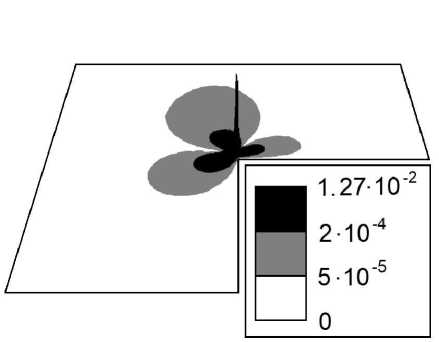
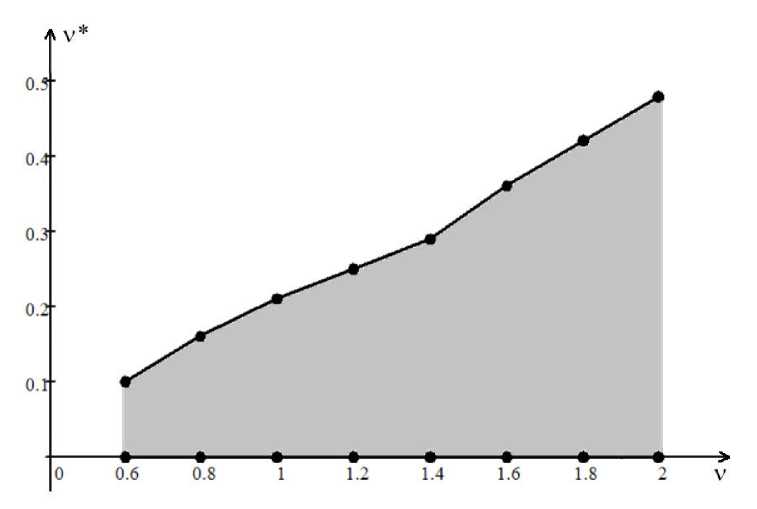
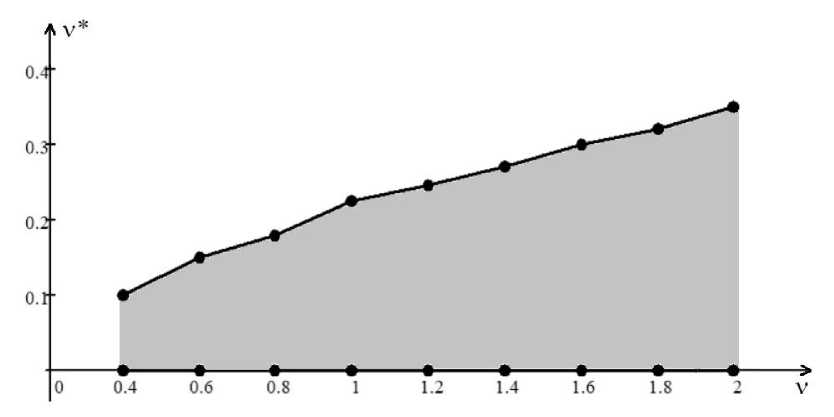
4.    Численные эксперименты. Определение области выбора свободных параметров подхода

В этом разделе представим результаты численных экспериментов решения задачи Стокса (6)–(8) с граничными условиями Неймана для двух конфигураций невыпуклой области (см. рис. 1).

Таблица 1. Зависимость погрешностей приближенного R_\nu-обобщенного решения, используя весовой МКЭ, от шага сетки h (по строкам) и степеней у и у* (^* — у*) в норме ^^u^ ^{- u}hllw2^(О). и^—3^

(А у)	(0.012, 2.0)	(0.0125,1.8)
h	у * — 0.375	у * — 0.35
0.01	1.201e-5	3.051e-5
0.005	6.004e-6	1.525e-5
0.0025	2.998e-6	7.615e-6

Рис. 1. Триангуляции областей Qi и Q2

Таблица 2. Зависимость погрешностей приближенного обобщенного решения, используя классический МКЭ, от шага сетки h (по столбцам) (v = у* = v* =0,5 = 1) в норме II^й - u ^h^w2,₀(П), ^Ш = 3г

h	0.01	0.005	0.0025
llu - uh|W2,0(Q)	1.647e-1	1.140e-1	7.822e-2

Покажем преимущество весового подхода над классическим МКЭ. Представим точное решение задачи (б)-(8) в полярных координатах (r, ^) в следующей форме:

^u1^(r, У) = r^kХ1,к⁽У), u2⁽r, У) = ^rl3kХ2,к⁽У), p⁽r, У) = ^rPk-17k⁽v)>

( Х1,к⁽У) V / X2,k ⁽У)

(1 + Рк )Лк (у) лк (у)

лк (у)

^{— (1 + Р}к ^)Лк⁽У)

) (^{sin у}), cos у

7к Ы =

(1+ Рк )²Лк (у)+Лк' (у)

Рк — 1

где

Лк (у) = cos((1 - Рк )у) - cos((1 + Рк )у) +

+(1 + Рк) 1 sin((1 + Рк)у) cos(wkРк) - (Рк - 1) 1 sin((Рk - 1)у) cos(wkРк), к = 1, 2, где Рк = min{Р : sin(Рwk) + Р sin Шк = 0 и Р > 0}. Тогда для Ш1 = 3Г, имеем Р1 ^ 0.54448, а для Ш2 = 5Г — Р2 ~ 0.67358. Таким образом, величина Рк определяет асимптотику поведения решения в окрестности точки сингулярности. При этом Ui / W^(Q),i = 1,2, и p / W^(^) — типичная ситуация для поведения решения в невыпуклой области с входящим углом на границе Г. Полагаем, что a = 1, h = NN, где N — количество отрезков разбиения по каждому направлению, h — шаг сетки.

Величину погрешности приближенного R\nu -обобщенного решения поля скоростей \bfu_\nu^h и приближенного обобщенного решения (v = v* = у* =0, 5 =1) поля скоростей u^h определяем как модуль разности между точным и приближенным решениями в нормах пространств W1 (П) и wUn) соответственно.

(а) h = 0.01

(б) h = 0.005

Рис. 2. Абсолютная погрешность первой компоненты поля скоростей приближенного

R^-обобщенного решения (v = 2.0, v* = у* = 0.375, 5 = 0.012), ш = 3Г

Результаты представлены в табл. 1–4 и рис. 2 и 3. Параметры \nu, \nu^\ast, \mu^\astи \delta, представленного весового МКЭ, определены экспериментально.

(а) h = 0.01

Рис. 3. Абсолютная погрешность первой компоненты поля скоростей приближенного обобщенного решения (и = 0, и * = ^* = 0, 5 = 1), ш = 3^

(б) h = 0.005

Рис. 4. Область подходящих свободных параметров метода для угла ш = 3^

Далее поставим себе задачу об определении области в переменных (v, v*)(^* = v*), для которой (в каждой ее точке) значение погрешности отличается от оптимальной не более чем на 6 процентов для всех величин h = 0.01, 0.005, 0.0025. В качестве радиуса 5-окрестности выбираем величину из диапазона [0.01, 0.03]. В экспериментах рассматриваем шаг изменения по переменной v*, равный 0.01 для всех положительных значений и шаг по переменной v, равный 0.2 из диапазона [0.6, 2.0] для Qi и [0.4, 2.0] для ^2- На рис. 4 и 5 показаны экспериментально найденные области выбора свободных параметров предложенного подхода.

Таблица 3. Зависимость погрешностей приближенного R_\nu-обобщенного решения, используя весовой МКЭ, от шага сетки h (по строкам) и степеней и и v* (^* = v*) в норме К - uh^w^(Q), ш = 5т

(6, v)	(0.0125, 2.0)	(0.015,1.8)
h	v * = 0.275	v*= 0.25
0.01	5.113e-6	1.756e-5
0.005	2.545e-6	8.731e-6
0.0025	1.277e-6	4.369e-6

Таблица 4. Зависимость погрешностей приближенного обобщенного решения, используя классический МКЭ, от шага сетки h (по столбцам) (и = ^* = и* =0, 6 = 1) в норме II^й- и^h|w2,₀(Q), ^ш = 5т

h	0.01	0.005	0.0025
IIй - иh|w2,0(Q)	8.329e-2	5.202e-2	3.262e-2

Рис. 5. Область подходящих свободных параметров метода для угла \omega

5\pi 4

Заключение

В статье введено понятие R_\nu-обобщенное решение задачи Стокса с граничными условиями Неймана в несимметричной смешанной постановки задачи. Компоненты решения определяются в множествах весовых пространств С.Л. Соболева. Построен весовой метод конечных элементов, основанный на определении конечно-элементной пары Тейлора—Худа 2го порядка.

Результаты численных экспериментов задачи Стокса с граничными условиями Неймана в невыпуклой области приводят к следующим выводам.

\bullet Приближенное обобщенное решение, полученное с помощью классического МКЭ, сходится к точному решению задачи со скоростью не выше O(h⁰'⁵⁴) и O(h⁰'⁶⁷) для Qi и

^2 соответственно в норме пространства W2o(Q) (табл. 2 и 4), в то время как приближенное R_y-обобщенное решение, полученное благодаря весового МКЭ, сходится к точному решению со скоростью O(h) в норме пространства W1 _y(Q) для всех величин входящего угла (табл. 1 и 3). Результаты согласуются с априорными оценками скорости сходимости приближенного решения к точному решению задачи (см. [1, 10]).

\bullet Результат достигается без сгущения сетки в окрестности точки сингулярности.

\bullet Предложенный весовой МКЭ позволяет производить высокоточные вычисления в окрестности вершины входящего угла и не дает погрешности распространяться во внутреннюю часть расчетной области, где решение обладает достаточной гладкостью (см. рис. 2).

\bullet Построена область подходящих свободных параметров подхода. Малому изменению параметров области соответствует малое изменение погрешности.

В дальнейших исследованиях, основываясь на определении Ry-обобщенного решения и предложенного весового МКЭ, предполагаем получить численные результаты для различных форм нелинейных уравнений Навье—Стокса, таких как конвективная, кососимметричная, консервативная и других.

Кроме того, классический МКЭ теряет в два раза свой порядок точности для краевой задачи с граничными условиями Дирихле—Неймана на сторонах входящего угла по сравнению с МКЭ для краевой задачи с граничными условиями Дирихле—Дирихле и Неймана—Неймана (см. [1]). Предложенный нами подход не теряет свой порядок точности — это было установлено для задачи теории упругости [19]. В одной из ближайших работ исследуем весовой МКЭ для рассматриваемой задачи в области с входящим углом на границе и граничными условиями Дирихле—Неймана на сторонах этого угла.

Работа выполнена в рамках государственного задания ИПМ ДВО РАН (№ 075-0045924-00). Результаты получены с использованием оборудования Центра коллективного пользования «Дальневосточный вычислительный ресурс» ИАПУ ДВО РАН .