О численном моделировании течений с прерывными волнами

Уравнения первого приближения теории мелкой воды [1], [2] широко применяются при численном моделировании процесса распространения прерывных волн (гидравлических боров), возникающих при полном или частичном разрушении плотины гидросооружения или при выходе крупных морских волн типа цунами на мелководье. Для более точного описания этих процессов широко применяются монотонные и квазимонотонные разностные схемы формально повышенной точности [3]. Одна из наиболее известных таких схем — TVD схема Хартена, [4] была построена путем модификации немонотонной схемы Лакса-Вендроффа [5], имеющей второй порядок аппроксимации на гладких решениях. В основе этой модификации лежат минимаксные процедуры коррекции потоков, в результате применения которых непрерывные разностные потоки схемы Лакса-Вендроффа становятся лишь Липшиц-непрерывными. Как следует из результатов, полученных в [6], это приводит к тому, что схема снижает до

первого порядок аппроксимации е -условий Гюгонио [7] на фронте нестационарной прерывной волны.

В настоящей работе показано, что схема Лакса-Вендроффа (имеющая непрерывные разностные потоки), в отличие от TVD схемы Хартена, со вторым порядком точности передаёт условия Гюгонио через фронт нестационарной прерывной волны. Это проявляется в том, что она сохраняет на грубой сетке второй порядок слабой сходимости [8] через фронт этой волны.

В то же время схема Лакса-Вендроффа принадлежит к классу явных двухслойных по времени консервативных разностных схем. В работе [9] получено, что все эти схемы имеют не более чем первый порядок слабой аппроксимации на разрывных решениях (повышенный порядок слабой аппроксимации гарантирует повышенный порядок сходимости во всех гладких частях рассчитываемых обобщённых решений). В данной работе показано, что схема Лакса-Вендроффа, в отличие от компактной схемы из [9] (имеющей повышенный порядок слабой аппроксимации на разрывных решениях), лишь с первым порядком приближает точное решение в окрестности точки градиентной катастрофы, в которой формируется прерывная волна. Это приводит к тому, что схема Лакса-Вендроффа (в отличие от компактной схемы) на мелкой сетке снижает до первого порядок слабой сходимости через фронт нестационарной прерывной волны. В результате в области влияния нестационарной прерывной волны точность вычисления по схеме Лакса-Вендроффа инварианта, проходящего через фронт прерывной волны, выше, чем по TVD схеме, и ниже, чем по компактной схеме.

Разностные схемы для уравнений «мелкой воды»

Векторная форма записи системы уравнений Сен-Венана первого приближения теории мелкой воды [2] для прямоугольного горизонтального русла при отсутствии трения имеет вид:

u t + f ( u ) x = 0,

Г h ) x Г q ) ^, f ( u ) = 2™! H^h

I q J         Iq / H + gH /2J где H(t, x) > 0 и q(t, x) — глубина и расход жидкости; g — ускорение силы тяжести (в расчётах полагалось, что g = 10).

Рассмотрим три разностные схемы, аппроксимирующие систему уравнений «мелкой воды» (1), (2). Первая из них — схема Лакса-Вендроффа [5], вторая — её TVD модификация Хартена [4], а третья — компактная схема Остапенко [9]. Первые две относятся к классу явных двухслойных по времени и симметричных по пространству консервативных разностных схем

Л h [ v П ] ^ ( v П ⁺¹ - v П )/ т + ( f , ^ - j _V2)Z h = 0,                                        (3)

где fj”1/2 = f(vnj-1+1,v”-1+2,™,vП+1,^); vn= v(пт,jh); X = тZh;                               (4)

т, h — шаги схемы по времени и пространству; f — функция численного потока, согласованная с потоком f системы (1) в смысле выполнения условия f (u,™,u,X) = f(u) VuG Rm, VXg R.

Временной шаг т в схеме (3) удовлетворяет условию устойчивости Куранта т < hl max lai (v nj )|,                                                                              (5)

/ i, j, n где ai(u), i = 1,2,...m, — собственные значения матрицы Якоби A(u) = fu системы (1).

В схеме Лакса-Вендроффа для системы (1), (2) поток (4) определяется по следующим формулам (при записи опущен индекс временного слоя n ):

fj+1/2 = fj+1/2 -    Е A^.R (v j ■ 1 '■(6)

• ^{2 Я} j = 1

Здесь

^+1/2 = (vk+1/2)2 <1/2;

• Vj+1/2 = ^a (vj+1/2); aj+1/2 = Lj+1/2(vj+1/2)Aj+1/2v;

a k есть j -тое собственное значение матрицы Якоби f u системы (1); R ^j и L ^k — соответствующие ему правый и левый собственные векторы.

TVD схема получается из схемы Лакса-Вендроффа (3)-(8), если в ней величины (7) задаются по формулам:

в + 1/2 = b ( V + 1/2 ^{+ Y} j + 1/2 ) « k + 1/2 " ^ j "^ + 1 ’                                               (9)

b ( x ) = { x ²/(4 e ) + e , I x l < 2 e ; I x I, I x l > 2 e }, e = 0.1,

• ^Y j + 1/2 = ^{{ A} j + 1/2 У j / ^a j + 1/2 ’ ^a j + 1/2 ^ ⁰ ; 0, ^a j + 1/2 = ⁰ i,

^ ^j = S^j + 1/2 ^{max[0, min(l} ^ ^j + 1/2 |’ ^ ^j - 1/2 s ' + 1/2 ^)] ’ S j + 1/2 = ^^П( ^ + 1/2 )’

^ ^j + + 1/2 = j[ b ( V k + 1/2 ) ^{- ( V} j + 1/2 ^{) 2 a j} + 1/2 .

В работе Хартена [4] показано, что схема (3)-(6), (8), (9) сохраняет второй порядок аппроксимации на гладких решениях, обладает TVD свойством в скалярном случае и является монотонной при аппроксимации линейных систем.

В отличие от первых двух схем, третья является компактной неявной, трёхслойной по времени, консервативной разностной схемой. Её операторная форма записи имеет вид

A ^ t . v n + A ^A 2 x f ( v n ) = - Ch- ^ x^ T ' v n ,                                  (10)

x т j th j т h4        j где

A_x = ( T h + 4 E + T - _h )/6, A t = ( Т ^т + 4 E + T ^-т )/6,

A xxxx = T 2 h - 4 T h + 6 E - 4 T - h + T - 2 h ,

A 2 x = ( T h - T - h )/2, A 2 1 = ( T ^т - T ^-т )/2

разностные операторы, определяемые при помощи операторов сдвига Tjvn = vn+j. Схема (10) является немонотонной при аппроксимации линейных систем и условно устойчивой по Куранту при Я = т/ h < 0.5. При этом она имеет третий порядок как классической, так и слабой аппроксимации. В данной работе при расчётах используется оптимальное значение коэффициента вязкости C = 1/96, которое гарантирует максимально быстрое затухание осцилляций в компактной схеме (10).

В следующем разделе приводятся результаты численных расчётов течений с нестационарными прерывными волнами по описанным выше трём схемам.

Результаты численных расчётов

Поставим для системы (1), (2) начально-краевую задачу

H (0, x ) = 2--arctg x , q (0, x ) = 0, q ( t ,0) = q ₀( t ), q ( t , X ) = q 1 ( t ),                 (11)

П в которой q0(t) и q1(t) — гладкие функции, согласованные с начальными данными в смысле выполнения следующих условий:

q 0(0) = 0, qi(0) = 0, q '.(0) = - gH (0,0) Hx (0,0) = a 0, q\(0) = - gH (0, X) Hx (0, X) = a1, a0 = —, a1 = —11arctgX I /(1 + X2).                                     (12)

П П V П )

Эти условия обеспечивают непрерывность точного решения и его первых производных в угловых точках (0, 0) и (0, X ) расчётной области. Предположим, что функции q ₀( t ) и q ₁( t ) выбраны так, что течение остаётся докритическим во всей расчётной области. Это гарантирует корректность поставленной начально-краевой задачи (1), (2), (11).

Начальные и граничные условия аппроксимируем следующим образом:

H j = H (0, jh ), q ⁰ = q (0, jh ), q n = q 0 (n T ), q N = q/n T ), 0 <  j <  N = XIh , n >  0.

На рисунках 1–4 показаны результаты расчётов для задачи (1), (2), (11), в которой X = 20, q ₀( t ) = a ₀ 1 , q 1 ( t ) = a 1 t , а для определения коэффициентов а ₀ и a 1 использованы формулы (12) (назовём эту задачу задачей I ). В процессе её решения в момент времени t = 1 в результате градиентной катастрофы формируется прерывная волна, распространяющаяся в положительном направлении оси x с возрастающей амплитудой и скоростью (см. Рис. 1).

Результаты, представленные на рисунках 1–3, для всех трёх схем получены при пространственном шаге основной сетки h = h _осн = 0.1, а на рисунке 4 — h = h _о cн /40 = 0.0025 . Временной шаг равен т = X h , где Я = 0.05 для задачи I (Рис. 1-4) и Я = 0.025 для задачи II (Рис. 5-6), что гарантирует устойчивость схем и максимально быстрое затухание осцилляций в компактной схеме. На всех рисунках приведены значения сеточных функций в чётных пространственных узлах разностной сетки. Треугольниками отмечено положение прерывных волн на оси x . Порядки слабой сходимости определялись по методу, описанному в [8], а относительные погрешности разностных решений — по методу Рунге, подробно изложенному в [6].

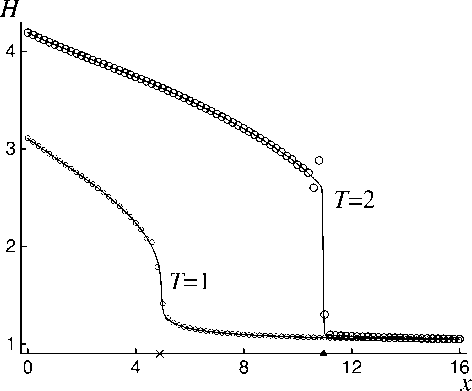
Рис. 1. Профиль глубины для задачи I

На рисунке 1 показаны результаты расчёта глубины H , полученные по схеме Лакса-Вендроффа (3)-(8), на моменты времени T = 1 (маленькие кружки) и T = 2 (большие кружки). Непрерывной линией, моделирующей точное решение, изображены результаты расчёта той же задачи по TVD схеме на сетке с пространственным шагом h /4 = 0.025.

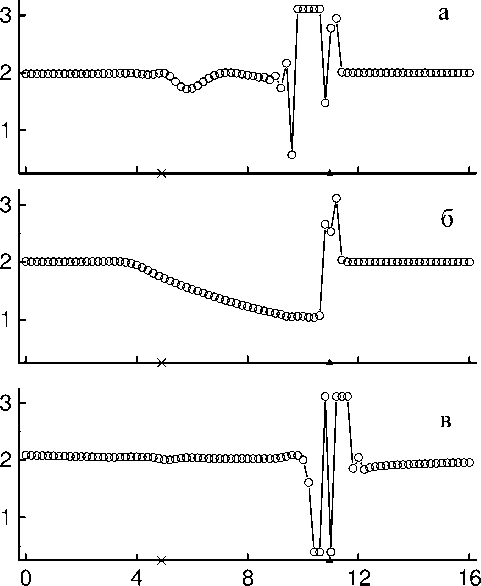
На рисунке 2 приведены порядки слабой сходимости. Из рисунка видно, что схема Лакса-Вендроффа (Рис. 2, а) и компактная схема (Рис. 2, в) сохраняют второй порядок слабой сходимости через фронт прерывной волны и, следовательно, со вторым порядком точности передают условия Гюгонио через её фронт, тогда как TVD схема (Рис. 2, б) этим свойством не обладает: у неё порядок слабой сходимости при переходе через фронт прерывной волны падает до первого.

На рисунке 3 дано сравнение относительных погрешностей 5w1 h и 5w2h, возникающих при вычислении инвариантов w1 = q / H + 2 gH, w2 = q / H — 2 gH                                    (13)

для осреднённого по рекуррентной формуле разностного решения

< x+5

v h ⁽ t ^, x ) = 47 J ^v h ^{1 (} t ^, x ') ^dx '^, i = ^1, ^ ^, l ^, v ⁰ = v h • 2 5

x — 5

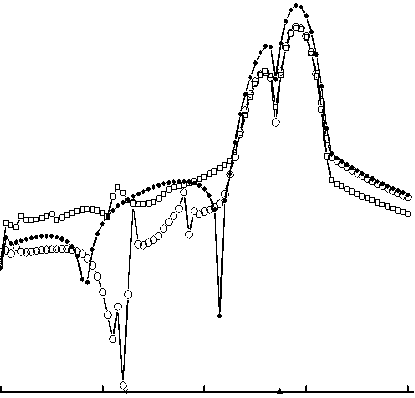
В выражении (14) интегралы приближённо вычисляются по формуле трапеций и где x = jh, 5 = 0.4, l = 5. Кружками показаны результаты расчёта, полученные по схеме Лакса-Вендроффа, точками — по TVD схеме, а квадратиками — по компактной схеме. Из рисунка 3 видно, что в области влияния фронта прерывной волны (4 < x < 10) точность вычисления инвариантов (13) по схеме Лакса-Вендроффа примерно на порядок выше, чем по TVD схеме. Существенно более низкая точность вычисления инварианта w2 , по сравнению с w1 за фронтом волны, объясняется тем, что инвариант w2 переносится в эту область вдоль характеристики, выходящей с фронта прерывной волны. Так как инвариант w2 переносит в гладкую часть точного решения информацию с фронта прерывной волны, то точность его вычисления на отрезке [6, 10] сразу за фронтом определяется точностью, с которой схема передаёт условия Гюгонио на разрыве. Из рисунка 3, б видно, что в данном расчёте схема Лакса-Вендроффа передаёт условия Гюгонио на порядок точнее, чем TVD схема, и на порядок менее точно, чем компактная схема.

r

x

Рис. 2. Порядки слабой аппроксимации на основной сетке h = 0.1

№ h i

W^l

-2

-4

-6

-8

16 x

а

Рис. 3. Сравнение относительных погрешностей вычисления инвариантов для задачи I

0         4         8         12        16

x

б

Обратим особое внимание на точку с пространственной координатой x = 4.9, которая отмечена крестиком на рисунках 1–3. Именно в этой точке на сетке с шагом h = 0.1 при t = 1 произошла «градиентная катастрофа» (см. Рис. 1), что вызвало образование прерывной волны. Из рисунков 2, 3 видно, что схема Лакса-Вендроффа и компактная схема, в отличие от менее точной TVD схемы, через свои порядки сходимости и относительные погрешности «помнят» (хранят информацию) о точке, в которой произошло формирование прерывной волны.

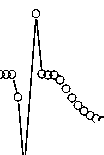
Для схемы Лакса-Вендроффа (Рис. 4, а) и компактной схемы (Рис. 4, б) приведены порядки слабой сходимости, получаемые при расчёте на существенно более мелкой сетке ( h = 0.0025). Для TVD схемы результаты расчёта порядка слабой сходимости на мелкой сетке качественно почти не отличаются от изображённых на рисунке 2, б, поэтому здесь они не приводятся. Поскольку данная сетка является очень мелкой, то значения сеточных функций приведены лишь в каждом восьмидесятом пространственном узле. Из рисунка 4 видно, что схема Лакса-Вендроффа, не обладающая повышенным порядком слабой аппроксимации и лишь с первым порядком приближающая точное решение в окрестности точки градиентной катастрофы, на мелкой сетке снижает до первого порядок слабой сходимости через фронт прерывной волны. Компактная же схема и при измельчении сетки сохраняет второй порядок слабой сходимости через фронт, что находится в полном соответствии с теоремой из [9]. На рисунках 5, 6 показаны результаты расчёта задачи (1), (2), (11), в которой полагается X = 16, q ₀( t ) = a 0 t - b ₀ t ², q 1 ( t ) = a₁t - bt ² + c 1 t 3 . Коэффициенты a ₀ и a 1 определяются из выражений (12), а коэффициенты b ₀, Ь 1 и c 1 — по следующим формулам: b ₀ = ( a ₀ T - 15)/ T 2 , Ь 1 = 10, c 1 = ( b₁T ² - 25) T 3 , где T = 3 (эту задачу назовем задачей II ). При её решении в момент времени t = 1 формируются две прерывные волны, распространяющиеся навстречу друг другу с возрастающей амплитудой и скоростью. Эти волны соударяются при t = 1.8 и x = 9 , в результате чего образуются две новые прерывные волны, распространяющиеся в противоположных направлениях (см. Рис. 5).

r

а

сшшшшшшшшг

б

9 «шжииииисшшшшшш^^

о

x

Рис. 4. Порядки слабой аппроксимации на мелкой сетке ( h = 0.0025 )

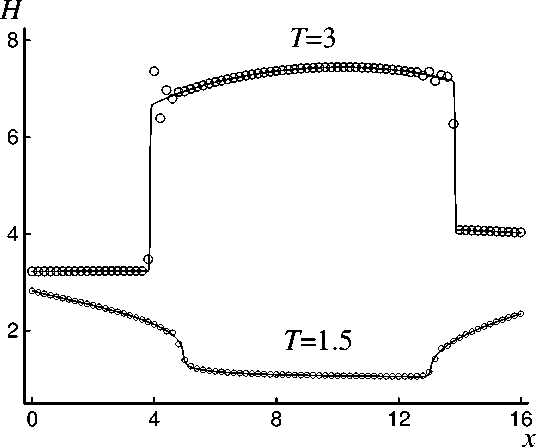
Рис. 5. Профиль глубины для задачи II

lg|3 w i h

!g б и ^ h l

4         8        12        16

x

U^^^_^^^_jj^^^_^^^_।^^^_^^^_।^_^^^_^_ l u_

0         4         8        12        16 0

а

б

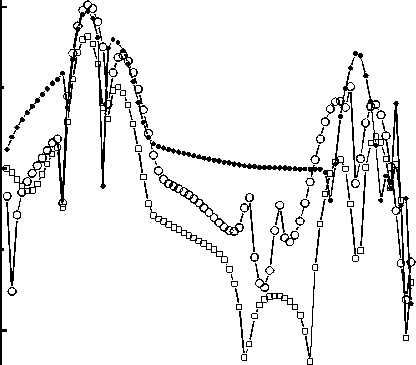
Рис. 6. Сравнение относительных погрешностей вычисления инвариантов для задачи II

Рассмотрим более подробно результаты численного расчёта задачи II.

На рисунке 5 показаны результаты расчёта глубины H по схеме Лакса-Вендроффа (3)-(8) на моменты времени T = 1.5 (маленькие кружки) и T = 3 (большие кружки). Непрерывной линией, моделирующей точное решение, изображены результаты расчёта той же задачи по TVD схеме на сетке с пространственным шагом h /4 = 0.025 .

На рисунке 6 приведены относительные погрешности инвариантов для осреднённого по формуле (14) разностного решения при T = 3. Значения, соответствующие схеме Лакса-Вендроффа, отмечены кружками, TVD схеме — точками, компактной схеме — квадратиками. Наибольший интерес представляет точность численного расчёта в области 4 < x < 14 между расходящимися ударными волнами, отмеченными треугольниками. Из рисунка 6 хорошо видно, что при 4 < x < 14 инварианты вычисляются по схеме Лакса-Вендроффа с более высокой точностью, чем по TVD схеме, и с менее высокой точностью, чем по компактной схеме.

Результаты приведённых численных расчётов демонстрируют, что схема Лакса-Вендроффа [5] занимает промежуточное положение между TVD схемой Хартена [4] и компактной схемой [9] относительно точности расчёта обобщённых решений с прерывными волнами. Она является более точной, чем TVD схема, и менее точной, чем компактная схема. Таким образом, монотонизация схемы Лакса-Вендроффа, связанная со снижением гладкости её разностных потоков при применении минимаксных процедур их коррекции, приводит к снижению реальной точности разностной схемы при расчёте нестационарных прерывных волн.

В заключение следует отметить, что в настоящей работе рассматривались прерывные волны, возникающие и распространяющиеся строго внутри расчётной области. Цель состояла в отделении проблемы, связанной с повышенной точностью сквозного расчёта прерывной волны, от проблемы задания разрывных начальных и граничных условий, которые бы эту повышенную точность сохраняли.

Автор выражает благодарность Владимиру Викторовичу Остапенко за ценные замечания и помощь в работе.

Работа выполнена при финансовой поддержке Совета по грантам Президента РФ для ведущих научных школ (грант НШ-2260.2008.1) и в рамках проекта фундаментальных исследований Президиума РАН № 16.2.