О деформации многослойной решетчатой пластинки диска зрительного нерва

Форму глазного яблока определяет плотная наружная оболочка, большую часть которой (93%) составляет склера. Недалеко от заднего полюса через склеру из глаза выходит зрительный нерв. Сплошного дефекта склеры здесь нет, а имеются ее истончения и множество мелких отверстий, через которые проходят пучки зрительного нерва. Участок склеры, через который проходит зрительный нерв, называют решетчатой пластинкой или (даже чаще) решетчатой мембраной ( lamina cribrosa ). Решетчатая пластинка играет важную роль в балансе внутриглазного и внутричерепного давлений. В монографии [4] отмечается, что «решетчатая пластинка состоит из нескольких параллельно расположенных листов плотной соединительной ткани, содержащей не только коллагеновые, но и эластические волокна. Количество их индивидуально и варьируется в широких пределах. Каждый лист имеет отверстия круглой или овальной формы различных размеров, некоторые из них имеют соединительные перемычки. Отверстия в различных листах совпадают, образуя канальцы, по которым проходят пучки нервных волокон… Самый задний лист плотнее и массивнее всех остальных».

В работах [6, 7] было высказано предположение, что ущемление нервных волокон в отверстиях решетчатой пластины происходит из-за вызванного повышенным внутриглазным давлением смещения составляющих ее пластин относительно друг друга.

В связи с этим в работе [1] рассматривались большие осесиметричные деформации тонкой безмоментной многослойной оболочки вращения в форме купола с упругими связями между слоями. Получено, что при увеличении внутриглазного давления наиболее сильные относительные смещения происходят на уровне последнего слоя, причем эти смещения увеличиваются к краю пластины. Это соответствует

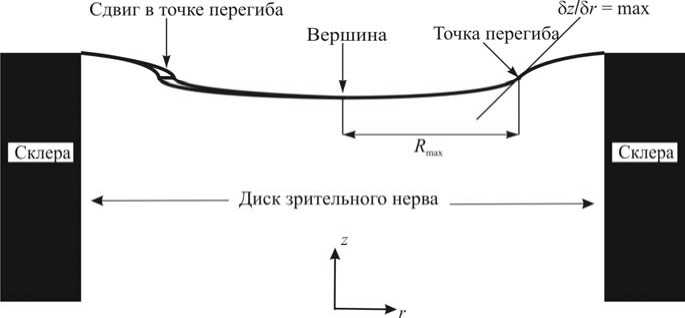
Рис. 1. Схема решетчатой пластинки глаза [8]

«специфическому нарушению зрительных функций» – «нарушениям на периферии и в парацентральной части поля зрения» [4, 5] и тому факту, что, как отмечается в монографии [5], «начальные дистрофические изменения в нервных волокнах определяются на уровне заднего края решетчатой пластинки склеры».

В работе канадских ученых [8] деформация решетчатой пластинки изучалась на основе экспериментальных данных и клинических наблюдений. Использовался метод сканирующей лазерной томографии, который способен выявлять региональные изменения в деформации диска зрительного нерва при сильных изменениях внутриглазного давления. Экспериментально было показано, что при увеличении внутриглазного давления появляется «точка перегиба» и форма прогиба решетчатой пластинки принимает вид, изображенный на рис. 1. Понятно, что модель безмоментной оболочки (или мембраны) не позволяет определить «точку перегиба» – точку, в которой, как отмечено на рисунке работы [8], производная от нормального прогиба по радиальной координате имеет максимальное значение.

Модель многослойной оболочки вращения

Рассмотрим моментную постановку ранее рассматриваемой задачи [1]. По-прежнему считаем, что имеем многослойную оболочку вращения с упругими связями между слоями. Расстоянием между слоями пренебрегаем, поэтому до деформации поверхность оболочки описывается функциями (рис. 2)

r o (ss 0 ), 2 o ( s 0 ), Ф о ( s 0 ), r' = cos Ф о , z 0 ' = sin Ф о , ( ) ' = d^l , (1) ds ₀

где s ₀, r ₀, z ₀, φ₀ – длина дуги, отсчитываемая от вершины купола, расстояние до оси вращения, вертикальная координата и угол между нормалью к оболочке и осью вращения соответственно.

После деформации форма оболочки описывается функциями r (s), z (s), Ф (s), (r ) = \ cos Ф , (z ) = X1 Sin Ф . (2)

Предполагаем, что слои могут проскальзывать друг по другу. Введем функции s ^k ( s 0 ) , k = 1,2,..., n , указывающие дуговую координату точки s 0 k- го слоя после деформации. Имеют место соотношения [3]

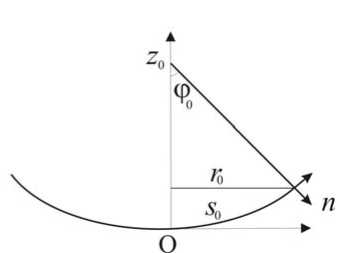
Рис. 2. Поверхность оболочки до деформации

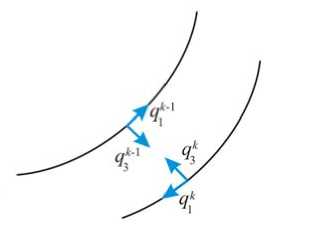
Рис. 3. Проекции интенсивности внешней нагрузки на k- й слой

kk

X* = dS-, X * =—, г* = r (sk), k = 1,2,., n,(3)

ds0

где λ₁ ^k и λ ^k ₂ – кратности удлинения срединной поверхности k -го слоя в меридиональном и окружном направлениях.

Из этих соотношений следует r0 (X2)' + cos ф0Xk - cos фkX* = 0, rk = r0X*.(4)

Уравнения равновесия k- го слоя оболочки в проекциях на касательную и нормаль имеют вид

( Г T ^k ) - T cos ф * + Г о (ф * ) T k + Г о X k X * ( q* i - 1 - q k ) = 0,

(Го Tk) - Tksin фk - Г,(р‘)Т + Го XkXk (q*-1 - q* ) = 0,(5)

(Го Mik) -Mk2 cos Фk - Го X*Tik = о, k = 1,2,^,n, где T1k, T2k и M1k, M2k– меридиональные и окружные усилия и моменты в k-том слое оболочки, отнесенные к единице длины после деформации, q1i и q3i – проекции интенсивности внешней нагрузки на k-й слой, отнесенные к единице площади после деформации и действующие с внутренней (qk-1 и qk-1) и наружной ( q1* и qk) стороны слоя (рис. 3).

Величины q ₁⁰, q ₃⁰, q ₁ ⁿ и q ₃ ⁿ определяются нагрузками, действующими на оболочку в целом. Будем считать, что оболочка находится под действием внутриглазного ( p 1 ) и внутричерепного ( p 2 ) нормального давления. Тогда 00 nn

Q 1 = ^о, Q з = P 1 , Q 1 = ^о, Q 3 = P 2 .

Величины q 1 ^k , q * , k = 1, 2,..., n - 1 - напряжения касательного и нормального взаимодействия слоев оболочки. Будем считать, что касательные напряжения являются заданными функциями относительного смещения слоев [1].

q^k_x = q k ( s о , A * ) , A * = s * ^{+ 1} - s * , * = 1,2, . , n - 1.

Усилия являются заданными функциями кратности удлинения слоев, зависящими от упругих свойств слоев. T k k kk k k kk

1      T 1 ^{( s} о , ^X 1 , ^X 2 ), T 2 T 2 ^{( S} о , ^X 1 , ^X 2 ), * 1, ²,•••, n*

Моменты являются заданными функциями кривизн

M ' = M 1 k ( s 0 , к * , к k ), M 2k = M 2k ( s 0 , к * , к k ), k = 1, 2,.., n.

Считаем для оболочки выполненным закон Гука [3]:

_t* = ^Ep h ⁰

¹    1 - v²

k

T ₂

^Ep^h 0 ^k 1 - v²

k

= E p ( h 0⁷ )³

12 ( 1 - v² )

2 ^k

12 ( 1 - v² )

. (Ф * )'       .           .

^к1 = -^T- ^- Ф « >     ^к 2

λ1

, / • к

1 Sin ф

k

0 V 2

sin Ф о ,

⁽ Ф 0 ) ' = -1.

R ₀

где h ₀ ^k – толщина k- го слоя решетчатой пластинки, E p – приведенный модуль упругости перфорированных слоев решетчатой пластинки, κ₁ ^k , κ ^k ₂– изменения кривизн нормальных сечений, R ₀ – радиус кривизны решетчатой пластинки.

Дополним систему (5) вытекающими из (6) уравнениями

k

T ₂

= E p h 0 ( X 2 - 1 ) + v T 1 ‘ ,     M

k = E p ( h 0' ) 3

к k + v M 1 ^k ,

( Ф ^k ) = X k

12 ( 1 - v² ) . E p ( h 0 ' ) ’

1 I            ( 1 - v²

M 1 ^k - vк k + — , X k =^----

R

k

E_ph ₀

^ T1^k - v(X k - 1) + 1.

Перейдем к проекциям U и V внутренних усилий соответственно на осевое и перпендикулярное к нему направления.

T 1^k = U ^k cos ф ^k + V ^k sin ф ^k , T k = U ^k sin ф ^k - V ^k cos ф ^k .

Введем безразмерные переменные по формулам

Vk( s,)       _Uk (s,)                          _Mi (s,)

^yk = „ , к , ^yn + k = пк , ^У 2 n + k = ^X 2 ^{( s} 0 ) , y 3 n + k =      , к * ’

E_ph ₀ ^k             E_ph ₀ ^k                              E_ph ₀ ^k r ₀

У 4 n + k

' n + 1          *     , ^y 5 n + 2

r ₀

s ₀

s ₀

Г * - радиус крайней параллели .

Таким образом, получена полная система 5 n + 2 дифференциальных уравнений относительно неизвестных U^k ( s ₀ ) , V ^k ( s ₀ ) , X k ( s ₀ ) , M 1^k ( s ₀ ) , ф ^k ( s ₀ ) , r₀ ( s ₀ ) , ф₀ ( s ₀ )

⁽ у * ) ' = ^- y ^{k cos y 5 n} + ^{2 - х} * у 2 n + k ( q 1 ^{k si}n y 4 n + k ^- q 3 ^k 3 c_OT y 4 n + k ) ,

У 5 n +1

k

^Уп + k c^{Os У} 5 n +2 ^- T 2 _ k\k (- k           _i_77 k _eini, 1

^{( y}n + k )                               ^X 1 ^У 2 n + k ( q 11 c^{Os У} 4 n + k ⁺ q 33 ^sin ^У 4 n + k ) ,

У 5 n +1

. V _ ^X 1 cos У 4 n + k ^- У 2 n + k cos У 5 n +2 ⁽ y 2 n + k )

y 5 n +1

,

где

( У 4 n + k ) ' = 12 ( 1 - V ⁵ ) У 3 n + k

⁽ У 5 n + 1 ) ' = cos У 5 n + 2 ,

*

( У 5 5 n + 2 ) ' = rb

R ₀

* ² r o h k ,

*

Г ^V    sin У 4 n + k

^R 0    ^У 5 n + 1 v ^У 2 n + k

-

sin У 5 n + 2

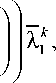
( )' =        , ds0

^T2k = ( У 2 n + k ^- 1 ) ^{+ V} ( У п + k cos У 4 n + k ⁺ У к sin У 4 n + k ) ,

^M 2 ^k

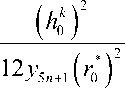
" sin У 4 n + k

V У 2 n + k

^{+ V} У 3 n + k ,

^ = ( Уп+k cos У4n+k + Уk sin У4n+k ) (1 - V ) - V ( У2n+k — 1) + 1, kp1p2*

q 33            3 k r o •

^Ep^h 0 ^k

В вершине купола выполнены граничные условия xk = 1, r0 = ф0=фk = 0, T1k = T2k при 50 = 0.                     (9)

Условие T k = T ₂ ^k обеспечивает конечность решений в вершине купола.

На краю пластины можно задать условия упругой заделки слоев

T k = c k ^{( 5 - 5} o ), Ф k = Ф о ^пР^и r o = r o* .                       ⁽¹⁰⁾

Параметры жесткости c k могут быть различными для разных слоев, и, судя по описанию структуры решетчатой пластинки [2, 4, 5], последний «наружный» лист решетчатой пластинки имеет наиболее жесткие граничные условия: c_N >  c_k при k <  N •

Напряжения касательного взаимодействия слоев оболочки принимаем в виде q = ak(5k+1 -5k)(rk -ro*).                                 (11)

Решение и результаты

При численном интегрировании краевой задачи (8)–(11) используется метод пристрелки: задаются значения U^k = u_k и V^k = v_k и получаемая задача Коши решается методом Рунге-Кутта до выполнения равенства r _o = r _o * .

Расчеты проводились для трехслойных пластин при различных параметрах c k и α k , учитывая что последний «наружный» слой является более плотным и массивным: h_N >  h_k при k <  N .

Ниже приведены результаты в безразмерном виде для случая c 1 / E p = 0,04; c 2 / E p = 0,04; c 3 / E p = 0,05.

На рис. 4 сплошной и пунктирной линиями показаны формы прогиба серединной поверхности верхнего ( k = 1) слоя пластинки соответственно до и после деформации. На рис. 5 представлены прогибы серединной поверхности последнего «наружного» слоя ( k = 3) после деформации (пунктирная линия) и до деформации (сплошная линия).

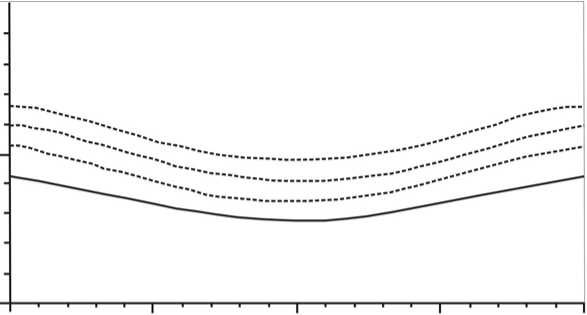
В общем виде прогиб деформированной пластины толщины h = 0,3 имеет форму, представленную на рис.6.

Таблица

s 0	M 1	M 3	φ 1	φ 3
0	0	0	0	0
0,5	0,00162	0,00117	0,25481	0,20004
0,6	0,00017	0,00008	0,27381	0,21576
0,65	–0,00070	–0,00056	0,27537	0,21773
0,7	–0,00165	–0,00127	0,27085	0,21523
1	–0,00941	–0,00687	0,08322	0,08379

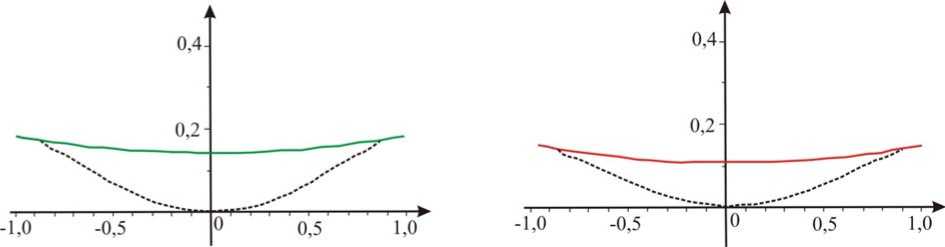
Рис. 4. Прогиб верхнего слоя до и после деформации

Рис. 5. Прогиб нижнего слоя до и после деформации

0,5              0              0,5               1

Рис. 6. Прогиб решетчатой пластинки после деформации

В таблице приведены безразмерные значения изгибающих моментов слоев M 1 = M i и соответствующих углов ф ¹ = ф i , i = 1,2,3 после деформации ( M 1 = M 2 , ф 1 = ф₂), полученные при численном решении рассматриваемой задачи. Видно, что в точке s 0 = 0,65 моменты меняют знак и углы достигают максимального значения, то есть точка s ₀ = 0,65 является «точкой перегиба».

Заключение

В широком диапазоне изменения параметров c k и α k при учете особенностей строения решетчатой пластинки (последний «наружный» слой является более плотным и массивным: h_N >  h_k при k <  N , а также более жестким [2, 4, 5]) получается, что, как и работе [3], наибольшие относительные смещения увеличиваются к краю пластины. Это соответствует тому факту, что «начальные дистрофические изменения нервных волокон определяются на уровне заднего края решетчатой пластинки склеры» [5].

В результате рассмотрения моментной постановки задачи [1] получаются численные результаты и форма прогиба, соответствующие экспериментальным данным [8].