О деформации сферической оболочки, заполненной несжимаемой жидкостью, при воздействии кругового растяжения по экватору

В данной работе при помощи пакета МКЭ ANSYS строится модель сферической трансверсально-изотропной оболочки, заполненной несжимаемой жидкостью и деформируемой экваториальными силами. Расчеты для мягкой оболочки проводились также по безмоментной теории оболочек. Далее рассматривается оболочка с характеристиками хрусталика глаза человека и исследуется изменение давления жидкости внутри хрусталика при аккомодации. Используется упрощенная модель хрусталика (как и в работах [4, 6]), не учитывающая влияние на него стекловидного тела.

Постановка задачи

Рассматривалась деформация мягкой сферической оболочки с радиусом нейтральной поверхности r ₀ , толщиной h ₀ (рис. 1).

Положение точки на срединной поверхности оболочки до деформации определяется в силу симметричности одной координатой – углом ϕ , после деформации – двумя координатами: r ( ϕ ) – расстоянием деформированного элемента оболочки от оси симметрии и ψ ( ϕ ) – углом между нормалью к элементу деформированной оболочки и осью x (рис. 2).

Обозначим деформацию и кривизну оболочки в направлении r = const как ε _χ и ρ _χ соответственно. Обозначим деформацию и кривизну оболочки в направлении χ = const как ε _r и ρ _r . Имеют место следующие соотношения [2]:

r . cos( v )               dr

£x =-----TT-1 Px =-------, 8r =--■ , x .

r ₀ cos( ф )              r           r₀ sm( y ) d ф

^^^^™

d v1, рr = -    sm(y).

dr

Уравнения равновесия элемента оболочки в направлении нормали к поверхности оболочки и меридиана x = const имеют вид pddr

Px£x+P r8 r = ^(1 -V), ^(£ rr) = £x x x        Eh 0        d v где E – модуль упругости оболочки в тангенциальном направлении.

Подставляя соотношения (1) в уравнения (2), после преобразований получим следующие уравнения:

‘ cos(v)-cos(y) +v_ + V sin(v) = PL(1 -v), (J2_)=__2r_.      (3)

r ₀ cos( ф )      r      r₀   r'          Eh 0          ^ sin( v ) J      cos( ф )

Решение данной системы дифференциальных уравнений с граничными условиями r (0) = R, r (n/2) = 0, v(n/2) = n/2

проводилось численным методом при помощи математического пакета

Mathematica 4.0.

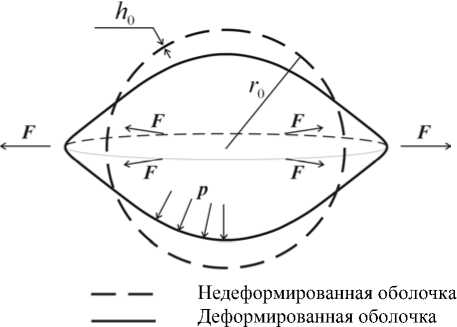
Рис. 1. Модель оболочки

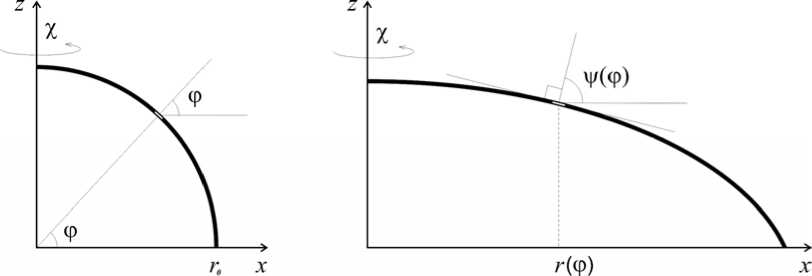
а                                        б

Рис. 2. Постановка задачи: а – оболочка до деформации, б – оболочка после деформации

Здесь R – радиус оболочки в экваториальной плоскости действия сил в деформированном состоянии.

Задача сохранения постоянного внутреннего объема оболочки решалась следующим образом. Задавалась деформация оболочки либо прикладывалась экваториальная растягивающая сила, а затем методом итераций подбиралось внутреннее давление, необходимое для поддержания постоянного объема. Решение этой задачи проводилось также при помощи пакета МКЭ ANSYS . Оболочка рассматривалась как осесимметричное 2 D тело вращения.

Результаты расчета и выводы

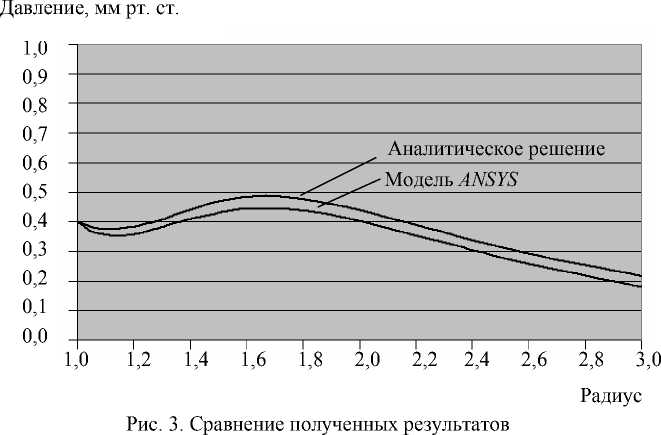
Для трансверсально-изотропной оболочки, у которой модуль упругости в направлении толщины значительно меньше тангенциальных модулей упругости, оба варианта решения данной задачи дают близкие результаты. При различных параметрах погрешность не превышает 10% (рис. 3). Здесь по оси x откладывается величина r' = R / r 1 - относительное изменение радиуса в экваториальной плоскости приложения сил, r ₁ – радиус растянутой только внутренним давлением жидкости оболочки. По оси у откладывается нормированное давление p ' , которое связано с обычным давлением 5 r по формуле p = —— p .

3 h ₀ E

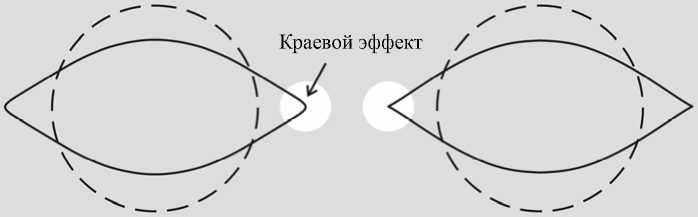
Поскольку модель, построенная в пакете ANSYS , учитывает моменты, возникающие в оболочке, т.е. учитывает краевой эффект, который «помогает» давлению сохранять постоянный объем (рис. 4), давление в данном случае оказалось ниже, чем для безмоментного аналитического решения.

Хрусталик приближенно представляет собой тонкую сферическую оболочку.

В работах [3, 5, 7] представлены следующие данные для глаза человека в Н возрасте 30 лет: E = 1,27 -106 2, коэффициент Пуассона v = 0,47. Толщина оболочки м2

(капсулы хрусталика) h ₀ по поверхности неоднородна, но можно приближенно считать ее равной 0,02 мм [4]. Диаметр хрусталика у разных людей колеблется от 6 до 7 мм. Для проведения расчетов необходимо представлять и величину начального внутреннего давления. Достоверные данные на этот счет отсутствуют.

Деформированная оболочка

Недеформированная оболочка

Рис. 4. Влияние краевого эффекта на форму деформации: а – модель ANSYS , б – безмоментная оболочка

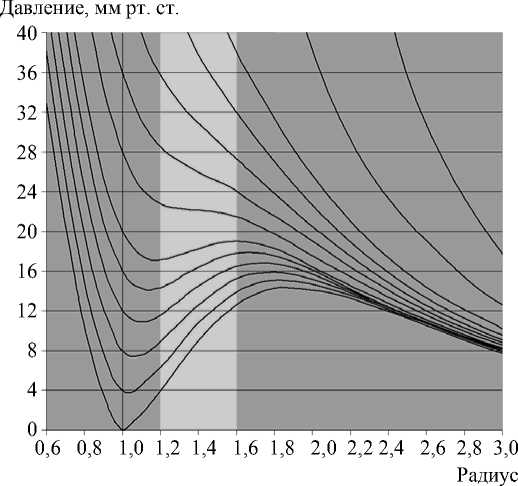
Рис. 5. Результаты для различных начальных данных

Давление можно выразить через начальное растяжение капсулы хрусталика

r ε= 1

r ₀

- 1, воспользовавшись формулой Лапласа p =

2Eh ε

1 - ν r1

Решения задачи для различных начальных значений внутреннего давления представлены на рис. 5.

При приложении сжимающей силы (r′ < 1) давление возрастает независимо от начального внутреннего давления жидкости и его рост значителен уже при небольших деформациях оболочки. Если величина относительной деформации r′ близка к 0,9, наблюдается практически линейный рост давления относительно величины деформации. Это согласуется с результатами, полученными в [1].

Если r ′ >1, то величина внутреннего давления зависит от начального внутреннего давления жидкости. Если p (1) <  24 мм рт. ст., то давление при приложении экваториальной растягивающей силы сначала незначительно падает и, достигая минимума, начинает снова расти, а после этого, достигая максимума, давление вновь падает, стремясь к нулю. Если начальное давление p (1) ≥ 24 мм рт. ст., то при растяжении оболочки экваториальной силой давление сразу начинает падать, стремясь к нулю.

Полученная зависимость позволяет описать изменение давления при аккомодации. Аккомодацией глаза называется процесс настройки его фокусного расстояния, позволяющий получить резкое изображение близлежащих объектов на сетчатке глаза. В данном случае форма линзы близка к сферической.

В состоянии, когда аккомодация отсутствует, линза уплощается под действием пассивного натяжения волокон пояска, которые натягиваются упругими составляющими сосудистой оболочки глаза.

Для наиболее актуальных величин относительных деформаций хрусталика 1,2–1,6 (выделено светлой полосой на рис. 5) можно сделать вывод о том, что при начальном давлении в хрусталике до 24 мм рт. ст. с ростом деформации внутреннее давление возрастает. При давлении в хрусталике более 24 мм рт. ст. с ростом деформации внутреннее давление может падать.