О дезарговой геометризации характеристики тела

В настоящей работе содержатся: 1) дезаргова геометризация характеристики р ^ 5 поля, в виде конфигурационной теоремы К_р, содержащей пару перспективных р- вершинников с центром S и освю I, где S ЭЕ /: 2) дезарговы геометризации характеристик 2 и 3 тел, в виде конфигурационных теорем Dg (1 2 3; 1' 2' 3') и L₇( 1 2 3; 1' 2' 3') соответственно; 3) доказателвства теорем: «Lio =Э К_р», «7з =ф> Д». «L7 -ФФ- 83» и «К_р -ФФ- р = 0».

В настоящей работе содержатся: 1) дезаргова геометризация характеристики р ^ 5 поля, в виде конфигурационной теоремы К_р, содержащей пару перспективных р-вершинников с центром S и осью I, где S DC I; 2) дезарговы геометризации характеристик 2 и 3 тел, в виде конфигурационных теорем D§ (1 2 3; 1' 2' 3') и £₇(1 2 3; V 2'3'), соответственно; 3) доказательства теорем: «Аю => К_р», «7₃ ^ ОД- «Ь₇ ^ 8₃» и «К_р ^р = О».

Эти результаты отличаются своей дезарговостью от результатов Фано [1], Рашевского [2], Цаппа [3] и Картеси [4] о геометризациях равенств 1 + • • • + 1 = п = 0, где п натуральное число.

Сначала найдем дезаргову геометризацию характеристики р > 3 поля в виде конфигурационной теоремы К_р, содержащей перспективные р-вершинники и представляющей некоторый обобщенный аналог малой теоремы Дезарга (Аю).

Конфигурационная теорема 1 (рис. 1). Пусть для точек 1, 2, .. . ,р общего положения, где р — простое натуральное число, выполняются следующие инциденции:

%' = [z 44>1, z + 2] П [z УУ2, z + 1] , z = 3,... ,p,p + l,p + 2,

Bi = [z, г + 1J П [z', z' + 1] , i = l,...,p, ^p T i = гУ^у'ф ^ \K,"K?\ приг^К, i'^S= [1, V] П [2, 2'] П ... П [P, P% (S, Въ ..., Вг_х,ВН1, ...,Bp).

Тогда выполняется и замыкающая инциденция

(S, в₁,...,в_г_₁,в_г,в_Н1,...,в_ру

Теорема К_р состоит из Зр + 1 точек и Зр + 1 прямых и имеет ранг 4.

Теорема 2. Некоторым ограниченным квазитождеством конфигурационной теоремы К_р является равенство р = 0 (р > 3).

<1 Пусть образующие точки в папповой плоскости имеют следующие координаты:

Р УУг — (2р 44>2z, ! + ••• + (z + 1)) — (2р 44>2z, 2 ^(z + 2)(z + l)), z — 0,...,р 44-1,

{Р = (2р, 1), Р^Т = (2р 442,1 + 2), Р^2 = (2р 444,1 + 2 + 3),...

2 = (4,р(р 441) • 2"1),Т = (2,р(р + 1) • 2"1), 3 = (6, (р441)(р 442) • 2"1)}.

Тогда, пользуясь аксиомами поля, получаем:

В_р_₂ = [Р 442, Р 441] П [Р, Р 443] = [р = эст + п] П [р = хт' + n'] = Z И V,

Р УУ2 ЭЕ I УУ 6 = (2р 444) • т + п

> О 3 = У^т о т = У^ • 2 ¹

П = 3^(2р^2)(^3 • 2"¹) = 3 + 3-2"¹(2р^2) = Зр

О [Р УУ2, Р О1] = [р = 443 • 2 ^ + Зр];

Р ЭЕ U УУ 1 = 2рт/ + п'

=ф т' = 443 • 2"¹,

Р 44>3 эе Z₂ 44 10 = (2р ууб)т' + п'

п' = 1^2р- (443-2"1) = 1 + Зр,

[р = (443. 2"^х + (1 + Зр)] = [F, Р^З],

Вр-2 — (^3 -2 Д ЭЕ Zoo,

В_р_₃ = [Р 4>3, Р 4>2] П[Р ээ4. Рээ!] = [у = -^2ж + 5р^>2]п[т/ = -^2ж + п] = (^2),

\Вр— 2, Вр — з] — Zqo-

Bp = [Р, 1] п [2, Р 4>1] = \у = ж/ + Z] П ^У = ж А + Н],

/1 =

р² ^р ЭЭб

4(3 ^р) ’

_ р2 Ар ^2

J ^- 4(1 ^р) ’

/ = fi О Ьр = Ьр 4> В_р ЭЕ Zoo-                     (1)

В1 = Ипи4ЧЧ^^14=^+1+т

ЭЕ Zoo ^ ^ = ^ ^ Р = 2р ^> р = 0 ^> Вт = (0).

Далее, имеем:

B_p_i = [Р У=Ц Р ^(i <=>!)] П [Р ^(i 4>2), Po(i + 1)] ЭЕ Zqo,

B_p_i = [у = ЖШ1 + ni] П [у = хт^ + п₂]

= ^j = ^х - 2“4 + 1) + 2"4 + 1)(2 + 2р ог)]

П \у = Цг + 1) • 2^-1ж + 2^-1 (^² + г + 2рг + 2р + г)]

= (^2"1(г + 1))

При г = 0 из (1) и (2), в силу (Bi, .. ., В_р, Sf имеем:

^В- ⁼ И) = ( ^Р4 Д^⁶ ) ^ ^^ ⁼ °’ f*³-^⁰'

Б, = (Д) = ( 4(4 ) ^ (P-S-DP = °- Р ^ 1- Р = 0:

(Р ^АгУ =[Р^>(г^>1),Р^>(г + 2)] П [Р ^(i + 1), Р ^(i 4>2)]

Цу = ЖП1 + По] П \у = xmi + пг₀]

Ци = Ц'1 + 2)2^-1 • х + 2^-1(<^² -^>г + 2рг + 4р + 4)]        (3)

П \у = Цг + 1)2^-1 • х + 2^-1(<^² + г + 2рг + 2р + 4)]

= (2р <^2z, y^p_iy),

Итак, из выполнения всех инциденций конфигурационной теоремы К_р следует, что р = 0 в тернарном кольце папповой плоскости, для любого простого числа р. Доказательство же соотношения «р = 0 ^> К_р» осуществляется обратным ходом выкладок, проведенных выше, опираясь на систему образующих точек К_р:

Р = (0,1), "Ро"г = <о2г, (г + 2)(г + 1)2"¹),..., 3 = (6,1),

2= (4,0), Т= (2,0), z = 1,...,р^1. ▻

Теорема 3. Для точек Р Ог = (Жр—, Ур—) и (Р ОгУ = (Жр—, У ^р^у У при указанном в доказательстве теоремы 2 наборе координат образующих точек К_р, имеет место:

Уущ-щ = Урщ + ^х’ г = 0,1,... ,р О1.

• < 1 В силу (3) имеем:

Ур- = 2"Чг + 2) (г + 1) = 2-^z2 + 3z + 2), у-^р—у = Ж(р—у ■ щ + По =       • 2(р ^z) + По

= 2^-1[ф£(г + 2)(р 4>г) У^-z² Ог + 2рг + 4р + 4]

= 2-^х(^2ф + 2z² о4р + 4г Ог² Ог + 2рг + 4р + 4)

= 2 ^(z² + 3z + 4) = Ур—i + 1, Vz = 0,.. .р •<=>!. [>

Теорема 4. Если в папповой плоскости выполняются все инциденции теоремы Кр, то точки пересечения соответствующих диагоналей ее р-вершинников 1. .. Р и 1'... Р' будут лежать на оси перспективы р-вершинников.

• < 1 В силу доказательств теорем 2 и 3, имеем:

"Рок = (2p^2fc,2"¹(fc + 2)(fc + l)),

(Р^ку = Др^кД-Цк² + 3fc + 4),

Ц = [F ^к, Р <^У = [т/ = xm + У,

Р ^к E3G Ц О 2 ^ Д + 2ук + 1) — 2(р <^fc) • т + t Р "^г E3G У О 2 ^z + 2)(z + 1) = 2(р <^z) • т + t

=4-

2 r((k + 2)(к + 1) о(г + 2)(z + 1)) = 2(р ок Ор + г^т, m = 02 2 (А; + г + 3),

Z' = WP ^ку, (Р Ог)' = [у = хп + s],

(Р ок)' эе

(Р Ог)' эе

1^ О 2 ^fc² + Зк + 4) = 2(р ок) • п + г

О

Z- О 2^-1(г² + Зг + 4) = 2(р Ог) • п + г

2 ²(fc² Ог² + 3(к О1)) = 2(г Ок)п О п = 02 ² (к + i + 3) = m.

Таким образом, прямые Z^ и Z' пересекаются в точке (ф£ ²(&+г + 3)) прямой Zoo-оси перспективы р-вершинников 1. .. Р и V . .. Р'. >

Примечание 1. Теорема 2 доказана пока лишь для папповой плоскости характеристики р. Аналогичным образом ее можно доказать и в дезарговой и муфанговой плоскостях характеристики р.

Примечание 2. Как известно из [4], геометрическое представление (Т_п) равенства 1 + -- - + 1 = п = 0, где тг — любое натуральное число, не содержит пар перспективных р-вершинников. Теорема же К_р состоит из двух р-вершинников 1. .. Р и V ... Р', имеющих ось I и центр S перспективы, причем S ЭЕ I.

О дезарговом содержании теоремы К_р гласит следующая

Теорема 5. В плоскости G_p, р У 2. справедлива импликация Тю О К_Р.

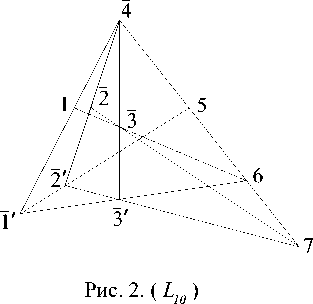
• < 1 Рассмотрим рис. 1 и 2. Расширим К_р диагоналями ее р-вершинников 1. .. Р и Р .. . Р' и рассмотрим пары перспективных трехвершинников: {1 23; Г^ Т}, {13 4; РТР},. .., {ТР^2Р^1; F(Р ^2)'(F ^1)'}, {IP^IP; Р (Р О1)' Р'У в каждой из которых в силу теорем 2 и 4 выполняются условия теоремы £ю, (рис. 2). Применив к каждой из них в указанном порядке теорему Lxo, мы убедимся в выполнении всех инцинденций теоремы К_р (выкладки опускаем). >

Ввиду проективного выполнения £ю в муфанговой плоскости справедливо

Предложение 5 (1). В муфанговой плоскости характеристики р ^ 2 теорема К_р выполняется проективно.

Так как в плоскости G_p, р ^ 2, теорема Dy проективно эквивалентна Рю (см. [8]), и кроме того, Вю О Рю, и Вю =4- К_р (см. теорему 5), то справедливо

Предложение 5 (2). В плоскости G_p, р ^ 2, из L₉ следует К_р.

Примечание 3. Характерной особенностью К_р является то, что при некоторых р ее можно образовать из р 441 точек. Например, Ку можно образовать из четырех точек: Ьф^В^ и В₄, следуя таблице инциденций вида (рис. 3)

S = [5, б⁷] П [В₄, В₅], Т = №, 5] П [б⁷, В7], 4 = [5, В₄] П [В^, б⁷], Г = [Т, S] П [б⁷, В^],

В₂ = \Ву В₅] П [Т, 4], 3 = [б⁷, В^ п [5, Г], З⁷ = [3, S] П [Т, 4], 2 = [5, З⁷] П [3, В^],

Т = [2, 5] П [Т, 4], В2 = [2, 5] П [3, 4], В, = [Т, 2] П [Г, П 4 = [4, S] П [5, З7], и замыкающим инцинденциям (S, В4, В2, В^. При этом остается справедливым соотношение «К^ 4> 5 = О». В самом деле, следуя указанной таблице инцинденций и замыкающей инцинденции Р5, при 5 = (0), 5' = (0,1), В5 = (0, -Ф^2), В4 = (<^1, 0), получаем:

Т = (^3, ^2), 4 = (0, 0), В₂ = (^3 • 4"¹, ^З"¹), 3 = (3, 4), V = (0, 4),

З⁷ = (З"¹ -2), 2 = (оо), ^ = (^3 • 2"¹, 44), В₃ = (442), В_х = (4^3, 4^6),

Щ = (442 ■ З"1), (Т,б,В4) 44 5 = 0.

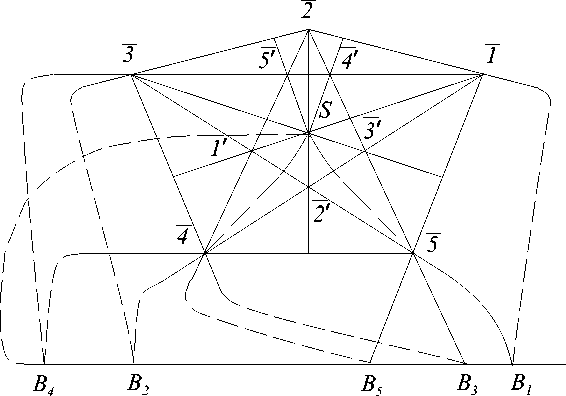
Рис. 3. ( K5 )

Для дезарговой геометризации характеристики 3 тела сначала напомним, что конфигурационная система D_s(S,/), где S ЭЕ I, есть конфигурационная теорема L7 [5] (рис. 4).

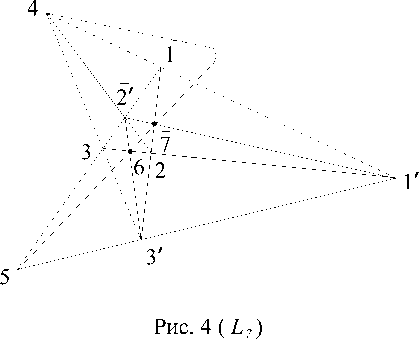
Теорема 6 (рис. 4). Имеет место следующее соотношение

L7 уу 1 + 1 + 1 — 0.

• <1    Если теорему L₇ задать образующими точками 6,1, 4, 2, таблицей инцин-денций:J = [4, 6] п/Д], Г = [1, 4] П [2, 6], ^ = [2, 4] П [4, 7], ЗМбД⁷] П [1, 2], 3 = [3', 4] П [V, 2], 5 = [1, 3] П [4, 6] и замыкающей инцинденцией (3, 5, 2'), то при следующих образующих точках: {6 = (0), 4 = (00), 1 = (0,0), 2 = (1,1)}, другие точки L₇ будут иметь координаты: 7 = (1), 1' = (0,1), 2' = (1,1 + 1), 3' = (1 + 1,1 + 1),3 = (1 + 1,1), 5 = Zoo П [у = жп] = (п). Далее, имеем: (1,3, 5) УУ 1 = (l + l)n, С2⁷,Т, 3, 5) УУ 1 + 1 = Ln =+ 1 + 1 + 1 + 1 = 1 =+ 1 + 1 + 1 = 0.

Обратным ходом рассуждений доказывается, что «1 + 1 + 1 = 0 +> L7». >  Выясним теперь геометрические взаимосвязи теорем £7, 83 (рис. 5) и 1З4 (рис. 6). (Проективная эквивалентность 83 и 1З4 доказана Рашевским в работе И)-

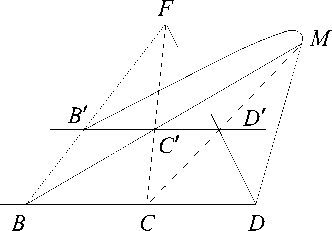
Рис. 5 ( 83 )

Теорема 7 [5]. В плоскости G3 характеристики 3 теорема L7 проективно эквивалентна теореме 83.

• <1    (1) 1З4 =У L7 (рис. 4 и 6). Рассмотрим два трехвершинника АС'С и FBD' с инцинденциями: F ЭЕ [С, СД В ЭЕ [Л, С], (D', А, С¹), М = [Л, F] П [В, С'\ П [С, D'Y В' = [Л, С'\ n\F₁B\₁D= [Л, С] П [F, D'^Q = [С, С'\ П [В, D'\ и докажем (М, D. Q. B'Y исходя из проективного выполнения 1З4 в плоскости. С этой целью выберем в L7 следующие 4 точки общего положения: В, С, В', С и построим 1З4 по вышеуказанной таблице инциденций. Тогда, в силу выполнения 1З4 в плоскости, в ней имеет место инцинденция ^M^BYD^QY Таким образом из 1З4 следует L7 в плоскости G3.

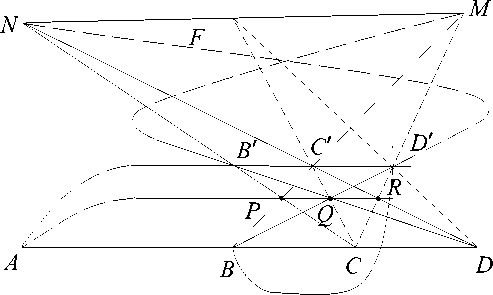
Рис. 6 ( 134 )

• (2)    L7 => 1З4. Докажем, что из L7 следуют все инцинденции теоремы 1З4. С этой целью рассмотрим в 1З4 шесть пар трехвершинников:

(I) ^ВВ^С'СА^ (II) [CC'P; D'DA}, (III) {MCG"; FD'B},

• (IV) }NCC'-,FB'D}, (V) }CC'M-,PRF}, (VI) }CC'N- RPF}.

Учитывая, что в L₇: (Q, С, СД (В, С, Л), В' ЭЕ [Л, СД В = [В', С] П [В, С'] П [Л, Q], прямая [F, ВД где F = [В, В'] П [С, СД D' = [В, Q] П [Л, СД инцинденция В, заключаем, что для трехвершинников (I) выполняются условия L7 и, следовательно, выполняется ее замыкающая инцинденция (Р, F, D, D'Y где D = [В', Q] П [Л, С]. Таким образом, (I) =У (Р, F, D, D'Y Аналогичными рассуждениями при учете (Р, F, D, D') устанавливаем, что (11)=/- (Р, A, R) и (F, R, В, B'Y Далее, сравнивая (В, Л, Q) и (В, Л, В) заключаем (В, Л, В, QY Если учесть, что в (III): (F,C,C'Y (О', М,С), (В, М,6') и точки В = [М, С'\ П VF.D'YR = ум^с^ n\F,BYQ = [С, С'] П [В, В'] лежат, в силу (III), на одной прямой (оси перспективы) и точка А = \С', D'] П [В, С] лежит на оси, то заключаем, что (A,F, MY Далее имеем, что (IV)=> (Л, F₁N). Сравнивая две последние инцинденции, мы приходим к (Л, F, М, NY Опираясь на рассуждения, аналогичные предыдущим, заключаем: (V) {В, D¹, Q, N). Так как в (VI): (С, С', F), (В, C.7V), (В, С', TV), (Q, В', В), Q = [С, С'] П [В, В], В' =

[С, 7V] П [Д, F], Р = \С\ N] П [Р, F], М = [Я, С] П [С⁷, F] П [TV, Д] в силу предыдущих инцинденций, то (D, Q, М, В'). Итак, из L7 следуют все инцинденции теоремы 1З4.

• (3)    83 =У L7. Пусть трехвершинники 123 и 1'2'3' имеют центр 4, точками пересечения сходственных сторон будут точки 5, 7, 6 и вершины одного (рис. 4) из них лежат на сторонах другого. Докажем тогда, что (4, 5,6,7). С этой целью рассмотрим в L7 пару коллинеарных точек 2' 3 5 и 7 2 3' с центром перспективы в точке 1'. В силу 83 (рис. 5), тройки (рис. 4) 2'3 5 и 2 3'7 из L7 также перспективны и с центром в 4. Следовательно, 83 =У (4, 5, 7). Аналогично этому, из перспективности троек 41'1 и З⁷ 6 2' с центром в точке 3, в силу 83, следует перспективность 4 I⁷1 и 6 2⁷ З⁷ с центром в точке 7 = [I⁷, 2⁷] П [1, З⁷]. Итак, 8₃ => (4,6,7).

• (4)    L7 => 83. В L7 выделим пару коллинеарных и перспективных троек точек 2⁷ 3 5 и 7 2 З⁷ (см. рис. 4) с центром 1 = [2⁷, 7] П [2, 3] П [5, З⁷]. Так как в L7 точки 4, 5, 7 коллинеарны, то тройки 2'. 3, 5 и 2, З⁷, 7 перспективны с центром в точке 4 = [2, Т\ П [3, З⁷] П [5, 7]. ▻

В заключение этой работы рассмотрим конфигурационную теорему D^.

Теорема D^ 8. (рис. 7). Пусть для точек (3, 6,1⁷), 2⁷, 4 бесконечной плоскости Фано выполняются следующие инцинденции:

[Й, 3] П [4, Й] = 2, З7 = [6, Й] П [3, 4], 5 = [Й, 3] П [Г, З7],

1 = [V, 4] П [2', 5], 7 = [I⁷, 2'] П [1, 2], тогда будут выполнятся и инцинденции (5, 6, 7) и (3, З⁷, 7).

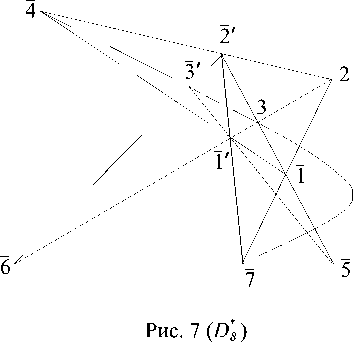
Теорема D^ состоит из 10 точек, 10 прямых и имеет ранг 8 (D^ ^ Dg\ Выясним теперь связи между D^ и 7з (рис. 8).

Теорема 9. В плоскости Фано G^ из 7з следует D^ проективно.

• <1    Пусть выполняются все инцинденции Dg (рис. 7), кроме (5,6,7) и (3, 3', 7). Тогда, применив 7з к четырехвершинникам П 3 2' 4 и 3 2' 3' 1', заключаем:

(1 = [V, 4] П [3, 2'], 2 = [V, 3] П [2', 4], 7* = [V, 2'] П [3, 4]) ^ (1, 2, 7 ),

(5 = [3, ^ П [V, З7], 6 = [3, Г] П [^ З7], 7' = [3, З7] П [V, г7]) ^ (5, 6, Т7),

(7 = Г = [Г, ^ П [3, З7, 4] n [Т, 2] = Т7 ^ (3, 4, 7) и (5, 6, 7)).

Аналогичными рассуждениями и выкладками доказывается, что при любом другом наборе образующих точек теоремы Dg из 7з следуют все инцинденции Dg. >

5/_ \ \

J/X6

• 1                       7           ³

Рис. 8 ( 73 )

Поскольку Dg содержит все инцинденции Dg и инцинденцию (7,3,4), то она есть частный случай Dg в плоскости Фано, и имеет дезаргово содержание.

(Существуют и другие дезарговы геометризации характеристики 2 (см. в [6].))