О динамике звуковых волн в трубке с эластичными стенками, заполненной пузырьковой жидкостью

Первые работы по акустическому анализу двухфазных жидкостей отмечены еще в конце XX века. Советскими учеными под руководством И.С. Кольцовой были проведены экспериментальные исследования затухания ультразвуковых волн в маловязких жидкостях с газовыми пузырьками, полученными электролитическим методом, результаты исследований отражены в работе [1]. Обнаружено, что в области резонанса пузырьков концентрационная зависимость коэффициента дополнительного затухания является функцией от частоты, причем до резонансной частоты и после резонансной частоты концентрационная зависимость коэффициента дополнительного затухания линейна. Данные, полученные учеными, в дальнейшем служили ориентиром для теоретических исследователей в этой области, опубликовавших свой труд в работах [2-5] и др.

Рис. 1. Схема задачи

В данной статье проведен акустический анализ волн в двухфазной жидкости, распространяющихся в трубке с эластичными стенками, выявлены некоторые особенности динамики звуковых волн.

Рассмотрим одномерные волновые возмущения, распространяющиеся в трубке малого радиуса, заполненной пузырьковой жидкостью. Стенки трубки считаем эластичными.

На рис. 1 представлено схематическое изображение системы, которое иллюстрирует трубку толщиной h, длиной L и радиусом a0 (L>> ао). Возмущения в системе возникают вследствие воздействия давлением по торцу трубки.

Основные уравнения

Запишем основные уравнения для описания движения волн в пузырьковой жидкости в труб ке с эластичными стенками с учетом радиальной инерции. Макроскопические уравнения сохранения масс, числа пузырьков, импульсов в односкоростном приближении имеют вид:

+ Э(^ = о, , — i,g,(1)

d t

d(nS) + d(nuS) _ о d td

d( puS) d( pu2 S )_d

1— — S .

d t        dx

Запишем кинематические соотношения для газожидкостной смеси:

al + ag — 1,

Физика

Pi= P^i,

P = Pg + Pl, a„ =—na n g3

где S - площадь поперечного сечения, n - число пузырьков, и - скорость, a - радиус пузырьков, a i - объемное содержание фазы, p i - плотность фазы.

Жидкость считаем акустически сжимаемой, газ - калорически совершенным:

pi = pо + C2( pP -

P O ),

Pg = Pg RTg, где pi - давление жидкости, p0 - начальное давление жидкости, Ci - скорость звука в жидкости, pg - давление газа, R - газовая постоянная, Tg - температура газа.

При описании радиального движения будем полагать, что жидкость несжимаема, скорость радиального движения складывается из двух слагаемых:

da w = —, w = wR+wA .

dt R A

Компонента w R описывается уравнением Релея-Ламба, соответствующим пульсациям одиночного сферического пузырька в безграничной несжимаемой жидкости:

dw_R 3 2 Л        ( pg - p )

а—R + -w 2 + 4v — = — g--- dt 2 ^{R l} a

0 ,

P l

где V j - кинематическая вязкость жидкости.

Добавка w A определяется из решения задачи о сферической разгрузке на сфере радиуса а в

несущей жидкости в акустическом приближении: w_A =

P g ^- P i

P i C ^ /3

Уравнение для давления внутри пузырьков записывается в виде: ^dpg _ 3yp о da 3( Y - 1) q ^^^^^^^^^^^^^^^^^^^^^^^^^1               ^^^^^^^» ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^в ^^^^^^^^^^^^^^^^^1  ^^^^^^^^  ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^»

dt       a ₀ dt      a ₀

где у - показатель адиабаты для газа.

Уравнение для интенсивности межфазного теплообмена после линеаризации примет вид:

q=-Р

f d T g

I d r

^{7 a} о

pg

1 емпература газа в пузырьках меняется по закону: T g = —— P о V ^а о

a 1 T

I ^T 0 .

В случае учета инерционных свойств стенок трубки считаем, что радиус трубки меняется по

закону:

^P w ( b о ⁺ h о ^{) 2 -} b о^{2 )}Д2^- = b ^{( p - p} о ^)- E "Г " ^{( b -} b о ) ,                     ⁽⁹⁾

д ² 1                    b о

где P _w - плотность материала трубки, b _о - начальное значение внутреннего радиуса трубки, h ₀ - толщина стенки трубки, E - модуль Юнга.

В случае пренебрежения инерцией стенок трубки при относительно небольших изменениях площади сечения трубки используем формулу связи избыточного давления в трубке и площади

поперечного сечения в виде:

Eh

A p i =-—A S . 2 a ₀

Начальные и граничные условия

Для инициирования волны в системе на границе z = 0 воздействует жесткий ударник по закону:

^U 0⁽ t ) = '

( ^Au 0 exP

^^^^^^^в

V

0, t >  t *

.       2 A t — t* / 2 ।

t * /6 J

, 0 <  t <  t *

,

где Аи0 - амплитуда скорости, t* - характерная протяженность импульса. На поверхности раздела фаз запишем уравнение теплового баланса aa

Так же на поверхности раздела фаз ( r = a ₀ ) зададим следующие граничные условия для системы:

rrr д a

T g = T l = T a , ^ t = w l = w g = w .

Кроме того д T

-y g = 0( r = 0), T i = 0( r = ~ ). д r

Линеаризованная система уравнений:

Для линеаризации уравнений будем считать, что изменение параметров по времени и координате происходит с минимальным скачком их соответственных значений.

Из уравнения масс (1) с учетом кинематических соотношений (4)-(6), условия (7) и уравнения сохранения числа пузырьков (2), после линеаризации и некоторых преобразований получено соотношение:

2 ^{д р} 1 0

“ ' ⁰ д t

^^^^^^^в

3ai0ag0p0 дa + у0P00 дS + ^  0 ди = 0

a ₀        д t      S ₀     д t      ^{10 P l 0} д х     "

Продифференцируем уравнение (10) по времени; уравнение импульсов (3) после линеаризации продифференцируем по координате, подставим его в (10). В результате преобразований имеем:

a l ² ₀ д ² p l   д ² p l   ^{3 a} i 0 ^a g 0 Pro д ² a

^^^^^^^B   ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^B   ^^^“

С² д t ²     д х ²

a 0       д t ²

+

^a i 0 ^p i o ^{д 2} S = 0

S 0     д t ²       ,

где S = n b ² .

Полученное уравнение при отсутствии пузырьков ( a _{g 0} = 0) и неизменной площади поперечного сечения ( S = const) совпадает с обычным волновым уравнением.

Уравнения пульсационного движения пузырька (8) и изменения радиуса трубки (9) после линеаризации принимают вид:

о д2a a 0 pi 0 ту+ 4

д t ²

ViPto дa

^p w ^{(( b} 0 ⁺ h 0 ) ^{2 — b}02 )’

a ₀

д ² b д t ²

д t

'

= P g

^^^^^^^е

' p l ,

_' Eh _'

= b 0 Pi —0— b .

b ₀

Уравнение состояния:

''

P g = ^p g 0

P g 0    ^p g 0

T ^'

+ -2- .

T g 0

Уравнения теплопроводности:

о о<3 ^T- P i 0 Ci d t	- 2 = r	d r	f. 2d T? Xr -- V      a r j		,	( r > a 0 ),	(15)
0c ^ T? P g 0 C g d t	- 2 A d r	f X g V	2 d t ; ^ r 2 g d r J	d P g + d t		, ( r < a 0 ).	(16)

Физика

Уравнение для давления в газе:

d P    3 y po d a   3( y - 1) X g 0                  g —                1	^ Tg-	.                               (17)
d t       a q   d t       a 0	d r V J	a

Результаты расчетов

Решение приведенной системы уравнений (11)-(17) ищем в виде затухающей бегущей волны

Pi , a , и, p g exp [ ( Kx - to t ) i ] , T = T ( r )exp [ ( Kx - to t ) i ] , b = b m exp [ ( to t ) г ] ,

K = k + to, Cp = -, где K - волновое число, to - частота возмущений, 5 и Cp - соответственно коэффициент затухания и фазовая скорость. Подставляя (18) в приведенную выше систему уравнений (11)-(17) и сокращая на экспоненту, имеем:

I ^K ) = ^а№ + ^3al 0 ^a g о a о ⁽ P im ^- P gm ) ^__ ^{2 n}b^ O j q ^р q __________

I w ) C    (aqV + 4Viito) Pim      f Eho                ,212 ) ’

^Л 0Г7-- ^p w ( ( ^b 0 ^{+ h} 0 ) ^- b 0 ) w

V b 0       ^v                       J

(Proto2a02 + 4viitoPiO ) Am- = Pim - Pgm , a0

У 1T =

² ₌4 A y^{g g} r ² d r

f

r

V

a 02 ^d r ² d r

2 1"

d r _j

f 2 d T ) z

I r I (r > a0), V dr J yg pgT0

+ (1 - Y )           (r < a о), pg0

2 pg        2  Am ygT0---= -3Yyg10 — pg0            a0

-

3( Y - 1) f ^d T g

₂      1/2

У1 = (-itoa0 /Xi)   , Xg =

a ₀

^ g ^p g 0 ^Cg

d r

, Xi =

I ,

/ a = a о

X

P i 0 C i ’

i V dr J a    g V dr J a ,

Tg = 1 = Tq, (r = a о), ^ = 0,  (r = 0), d r

Ti = 0, (r = ~).

где c_i - теплоемкость жидкости.

Численный анализ

Расчеты проводились для следующих физико-химических параметров системы. Вода: vi = 3,6 -103 м2/с, ci = 4200 Дж/кг^К, pi = 103 кг/м3, ^ = 0,6 м^кг/К^с3, Ci = 1500 м/с, p0 = 105 Па. Воздух: p = 105 Па, а = 0,001, X, = 0,026 м^кг/К^с3, P = 1,29 кг/м3, с„ = 1006 Дж/кг^К. Труба g   gg      g    g имеет следующие геометрические параметры: b0 = 2 • 10 2 м, h0 = 5 -10 3 м. Материал трубы -поликарбонат: ps = 1200 кг/м3, E = 2,13-109 Па.

Для случая пузырьковой жидкости результаты расчетов представлены в виде графиков, выражающих зависимость коэффициента затухания 5 от частоты to .

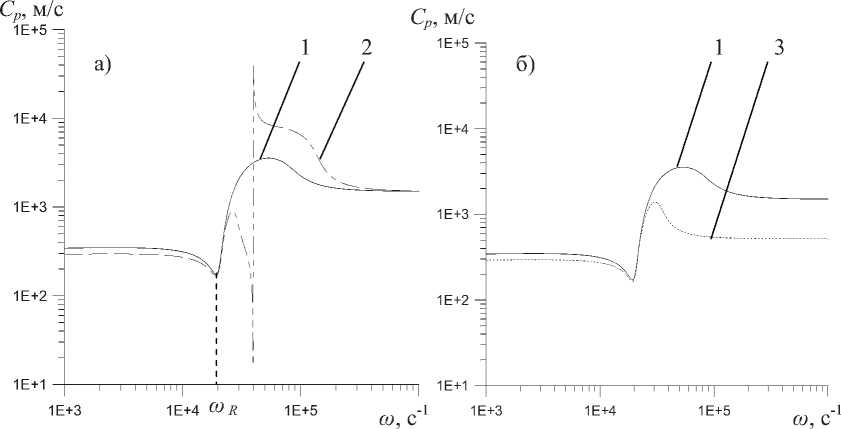
Рис. 2. Зависимость фазовой скорости C p от частоты to

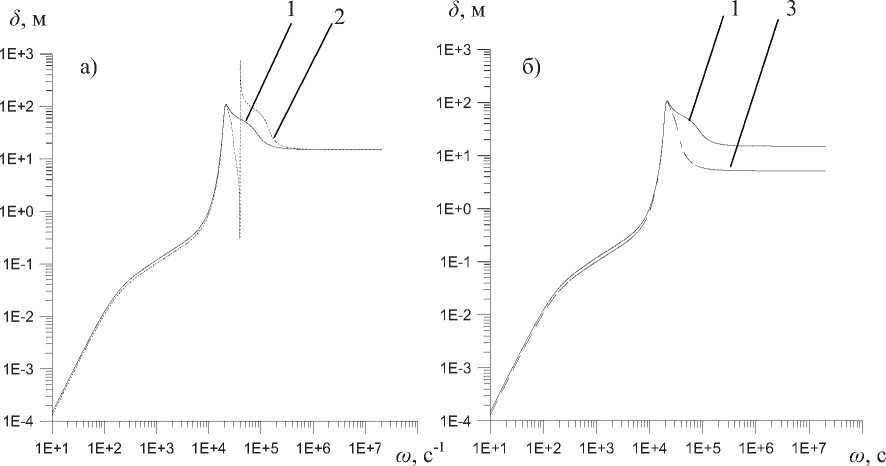
Рис. 3. Зависимость коэффициента затухания 5 от частоты to

На рис. 2. представлены зависимости фазовой скорости C_p от частоты to для двухфазной жидкости. На рис. 2, a , б черная сплошная линия (1) соответствует случаю распространения акустических волн в трубке с «жесткими» стенками, штрихпунктирная линия (2) на рис. 2, a - случаю распространения акустических волн в трубе, стенки которой обладают инерционными и эластичными свойствами. Случаю распространения звуковых волн в безынерционной эластичной трубке соответствует пунктирная линия (3) на рис. 2, б . Видно, что в низкочастотной области ( to ^ to R ) равновесная скорость акустических волн в пузырьковой среде (310 м/c), находящейся в трубке с «жесткими» стенками, чуть выше значения аналогичного параметра для волн в трубке с податливыми стенками, которая принимает значение 266 м/c вне зависимости от учета радиальной инерции стенок трубки. Радиальная инерция стенок трубки оказывает значительное влия-

Физика ние на скорость и коэффициент затухания при частотах to, превышающих частоту Минаерта юс : на рис. 2, а видно, что кривая (2) терпит разрыв вблизи частоты to = 4,43^104 с-1, таким образом, для акустических волн в двухфазных системах, находящихся в эластичной трубке, стенки которой обладают радиальной инерцией, свойственна полоса непропускания - диапазон частот, при которых акустические волны не распространяются. Полоса непропускания в нашем случае составляет 0,02^104 с-1. Далее по рис. 2, а кривая в области высокочастотных колебаний (to >> toc) выходит на стационарное значение фазовой скорости, называемое замороженным, которое близко к скорости звука в чистой жидкости (1500м/c). Этого же значения достигает фазовая скорость после небольшого скачка по кривой (1). Для кривой (3) значение замороженной скорости значительно ниже - достигает 490 м/с .

На рис. 3, а , б представлены графики, выражающие коэффициенты затухания акустических волн в двухфазной жидкости, находящейся в трубе с «жесткими» стенками (1), эластичными стенками, обладающими массой (2), эластичными стенками без радиальной инерции (3). Очевидно наличие полосы непропускания для пунктирной кривой (2), идентичной наблюдаемой на рис. 2, а . В случае акустических волн в двухфазной жидкости в безынерционной эластичной трубке (линия 3) коэффициент затухания при частотах, превышающих частоту Минаерта to _c , оказывается меньше значений, соответствующих случаю акустических волн в двухфазной жидкости в «жесткой» трубке (линия 1).

По результатам исследований сформулировали следующие выводы:

• 1)    для динамики акустических волн в двухфазных жидкостях, находящихся в трубке с эластичными стенками, обладающими радиальной инерцией, существует полоса непропускания. Значение фазовой скорости в низкочастотной области ниже аналогичного параметра для акустических волн в пузырьковой жидкости, распространяющихся в трубке с «жесткими» стенками. К тому же значения замороженных скоростей в обоих случаях едины;

• 2)    в низкочастотной области значение фазовой скорости акустических волн в пузырьковой жидкости в трубке с эластичными стенками, не обладающими радиальной инерцией, несколько ниже, а коэффициент затухания близок по значению аналогичному параметру для акустических волн в пузырьковой жидкости в трубке с «жесткими» стенками. А в высокочастотной области фазовая скорость и коэффициент затухания акустических волн в трубке с эластичными стенками без радиальной инерции значительно ниже аналогичных параметров для акустических волн в пузырьковой жидкости в «жесткой» трубке.