О дискретных моделях колебательных систем

Самым распространенным подходом к численному моделированию динамических систем является переход к дискретному времени путем конечно-разностной аппроксимации дифференциальных или интегральных операторов в их уравнениях движения [1]. При этом происходит замена исходной системы (НВ-системы), функционирующей в непрерывном времени, динамической системой с дискретным временем (ДВ-системой). Все дальнейшие результаты – это результаты анализа характеристик ДВ-системы. Хорошо, если они с определенной точностью воспроизводят характеристики НВ-системы. Но так как законы НВ-динамики и ДВ-динамики, строго говоря, различны, это далеко не всегда имеет место. Например, ДВ-система не может одновременно иметь частотную и импульсную характеристики аналогового прототипа – хорошо известный факт из области цифровой обработки сигналов [2].

Различия в свойствах НВ- и ДВ-систем, как правило, становятся пренебрежимо малы, если выбрать шаг дискретизации по времени (интервал дискретизации) много меньшим, чем характерный временной масштаб системы. Но уменьшение шага, естественно, приводит к увеличению времени вычислений и может сделать численный эксперимент неприемлемо продолжительным. Поэтому практическое значение имеют интервалы дискретизации, составляющие существенные доли временных масштабов. В этой ситуации результаты исследований упомянутых различий НВ- и ДВ-систем могут быть полезны при выборе метода моделирования динамической системы.

В настоящей работе для численного моделирования нелинейных колебательных систем (КС) предлагается использовать алгоритм, основанный на сохранении импульсного отклика линейного осциллятора. Частотная характеристика эквивалентной алгоритму ДВ-системы сравнивается с частотными характеристиками ДВ-систем, соответствующих явным методам Рунге – Кутта.

1.    Импульсно-инвариантный метод моделирования

В качестве базовой дифференциальной модели нелинейной КС рассмотрим уравнение d2 u to0 du 2      2

+        + to o u -to o f ( u , t ) ,                   ⁽¹⁾

dt2   Q dt где too и Q — собственная частота и добротность системы; f(u, t) – функция, описывающая реактивную нелинейность и содержащая аддитивное внешнее воздействие на КС. В дальнейшем будем использовать также ее запись с выделенным воздействием: f (u, t) - g (u(t)) + e(t). В качестве физического объекта, моделируемого уравнением движения (1), можно предложить, например, колебательный контур с нелинейной емкостью, возбуждаемый источником напряжения. В этом случае осциллирующая переменная u(t) – напряжение на емкости контура.

Альтернативной (1) формой описания КС является ее интегральная модель в виде уравнения Вольтера второго рода [3]

t

u ( t ) = J f ( u (t), t ) h ( t - t) d т + U ( t ).                 (2)

Здесь функция времени U ( t ) описывает свободные колебания в контуре.

Ядро уравнения (2) h(t - т) — импульсная характеристика контура, удовлетворяющая уравнению d2h ®0 dh   2K    2$M

^{+        + m} o ^h = ^m o ^{5 (} t )                      (3)

dt2 Q dt с дельта-функцией в правой части и нулевыми начальными условиями. Отметим, что свободные колебания U(t) также подчиняются уравнению (3), но зависят от начальных условий. Решением (3) при t > 0 является функция m2    Г m ^

h ( t ) = — exp I 0- t I sin(^ 1 t ) .

Ю 1      v 2 Q J

Частота осцилляций к> 1 в высокодобротном контуре с точностью до величин второго порядка малости по параметру ц = 1/ Q совпадает с ю ° :

to 1 = ю ° 1

- 4 Q 2 ⁼ “ ° ⁺ O ^(ц 2 ) '

Потому в дальнейшем, считая эти частоты одинаковыми, будем использовать импульсную характеристику

h ( t ) = m ° exp

- 2 Q t J ^{sin( m} o t ).

Легко установить, что отсчеты характеристики (4) на равномерной временной сетке t n = n A t при n > 2 удовлетворяют разностному уравнению

D 2 { h ( t n ) } ^ h ( t n ) - 2а cos ( m ° A t ) h ( t n - 1 ) + ⁺ 0 2 ^{h (} t n - 2 ) = °, где

„ Г ®0 □ а = exp - °- At ,

V 2 Q J и начальным условиям

h ( t ° ) = h (0) = 0, h ( t 1 ) = h (A t ) = аю ° sin(m ° A t ).

Последовательность отсчетов применим h(tn) при дискретизации времени в интегральном уравнении (2). Для этого создадим дискретизирующую последовательность to hd(t) = At ^ h(tm)5(t - tm).                     (6)

m = 0

Импульсную характеристику h(t - т) в (2) заменим последовательностью (6). После интегриро- вания для значений решения на временной сетке tn получим уравнение дискретной свертки u (tn) =

= A t ^^f ( u ( t n - t m ), t n - t m ) h ( t m ) + U ( t n ).

m = 0

Это уравнение имеет вторую форму n

u ( t n ) = a t ^ f ( u ( t k ), t k ) h ( t n - t k ) + U(t n ).      (7)

k = 0

Теперь обе части уравнения (7) подвергнем воздействию разностного оператора D 2 ( 0 } (см. (5)). При n > 2 это приводит к следующему результату:

D 2 { u ( t n ) } = A th (A t ) f ( u ( t n - A t ), t n - A t ) .        (8)

Отметим, что в процессе преобразования правой части (8) использованы равенство h (0) = 0, уравнение (5) и аналогичное ему уравнение D 2 { U ( t n ) } = 0.

Следует обратить внимание на то, что равенство h (0) = 0 приводит к зависимости правой части (8) от момента времени t_n - A t = t_n - 1 . А это, в свою очередь, позволяет получить явную разностную схему.

Таким образом, алгоритм моделирования нелинейных колебаний определяется рекуррентной формулой un - 2а cos (m°At) un-1 + а2un-2 = = A th (At) f (un-1, tn-1),

где n = 3, 4, ..., а для значения u1 и u2 с помощью выражений u1 = ^ A th (At) f (u °, t ° ) + U

1 ,

u 2 = A th (2A t ) f ( u ° , t ° ) + U 2

в соответствии с интегральным уравнением (2) определяются по начальным условиям u ° , i t ° .

2.    Трансформация вычислительного алгоритма в ДВ-систему

Теперь, считая (10) уравнением движения, представим конечно-разностный алгоритм в форме ДВ-системы. Для удобства представления выделим в правой части (10) аддитивное воздействие: f ( u , t ) = g ( u ( t ) ) + e ( t ). Чтобы подчеркнуть смысл индекса n как дискретного времени, введем новое обозначение: u [ n ] = u_n . Кроме того, все частоты будем измерять в единицах частоты дискретизации ю d = 2п / A t , так что m ° A t = 2nQ ° . Это весьма удобный способ измерения частот.

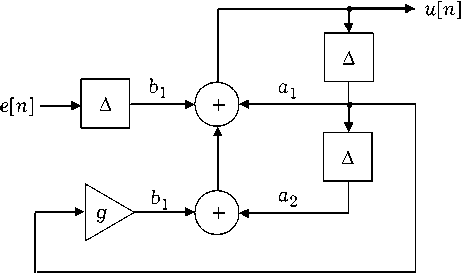
Рис. 1. Блок-схема нелинейной ДВ-системы (11)

Например, значение Q o = 0.167 соответствует шести отсчетам на период.

Таким образом, ДВ-система, соответствующая разностному алгоритму (10), определяет-

ся уравнением движения

u [ n ] = а .1 u [ n - 1] + a 2 u [ n - 2] +

+ b1g (u[n - 1]) + be[n - 1], где a1 = 2acos (2nQ), a2 =-a2, b1 = 2naQ0 sin(2nQo), a = exp (-nQ / Q).

В динамике систем с дискретным временем ДВ-система (11) становится самостоятельным объектом исследований.

Структура связей в ДВ-системе (11) наглядно отображается блок-схемой, приведенной на рис. 1. С ее помощью нетрудно установить, что выходной сигнал u [ n ] формируется суммарным воздействием на линейный ДВ-контур внешнего сигнала e [ n - 1] и внутреннего сигнала обратной связи g ( u [ n - 1] ) . При этом форма частотной характеристики линейного ДВ-контура играет важнейшую роль в формировании u [ n ]. Частотные характеристики НВ- и ДВ-контуров в (1) и (11) описываются точными формулами:

H a ( j Q )

H d ( j Q )

= 7-----^------ и

(q2 -qO ) + jQQ0 / Q b1 Z :(jQ)

1 - a 1 Z ^{- 1} ( j Q) - a 2 Z "" ² ( j Q)’

где Z ( j Q) = exp( j 2nQ).

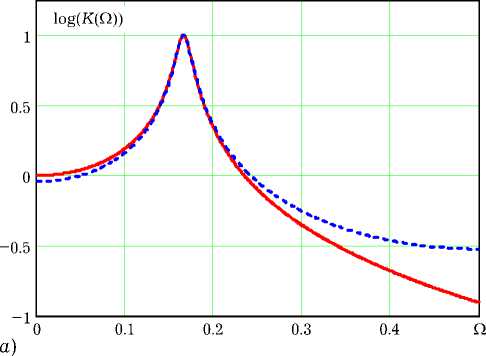
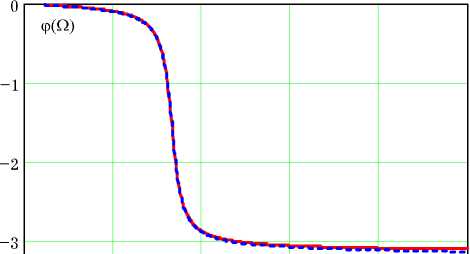
На рис. 2, а показаны графики амплитудно-частотных характеристик Ka (Q) =| Ha (jQ) | (сплошная линия) и Kd (Q) =| Hd (jQ) | (пунктирная линия) контуров с собственной частотой Qo = 0.167 и добротностью Q = 10. Фазочастотные характеристики (рис. 2, б) при этом с графической точностью совпадают. Из этих и аналогич- ных им графиков следует, что ДВ-система (11)

% 0.1 0.2 0.3 0.4 n 6)

Рис. 2. АЧХ и ФЧХ НВ- и ДВ-контуров хорошо воспроизводит частотные свойства аналогового колебательного контура в области резонанса, а наибольшие различия в свойствах наблюдаются в области высоких частот. Если в нелинейной системе сигнал обратной связи g (u[n - 1]) кроме колебаний основной частоты содержит их гармоники, то следует ожидать, что значения u(tn), полученные с помощью численного алгоритма (10), будут отличаться от истинных завышенным уровнем гармоник.

3.    Дискретные отображения осцилляторов методами Рунге – Кутта

Представляет интерес сопоставление частотных характеристик (12) с характеристиками ДВ-осцилляторов, порождаемых в результате применения к линейному НВ-осциллятору явных методов Рунге – Кутта [4] – традиционных методов численного моделирования динамических систем. Для обозначения таких ДВ-систем можно использовать также термин «дискретные отображения».

Семейство явных алгоритмов Рунге – Кутта порядка p = 1 ^ 4 ( RK 1 ^ RK 4) можно определить общими формулами [4]

p

У n + 1 = y n ^{+ A} t ^ ^b s ^k s , s = 1

^k 1 = f ( У n , t n ) , ^k 2 = f ( У n ⁺ a 21 ^k 1 ^A t , t n ^{+ c} 2 ^A t ) , ^{(13) k} 3 = f ( У n ^{+ (} a 31 ^k 1 ⁺ a 32 ^k 2 ^{) A} t , t n ^{+ c} 3 ^A t ) , ^k 4 = f ( ^y n ^{+ (} a 41 ^k 1 ⁺ a 42 ^k 2 ⁺ a 43 ^k 3 ^{) A} t, t n ⁺ c 4 ^A t ) , где числовые значения коэффициентов a , b и c для каждого из порядков р рассчитываются методом подгонки рядов Тейлора [4].

Для линеаризованного осциллятора (1) вектор-функция f ( y , t ) правых частей уравнений состояния системы имеет следующий вид:

T

.      (14)

– для RK 3:

A 11 = 1 — 2n 2 Q ° 2; A 12 = 2nQ °	4П Q ° 3 Q 3 , 1 2 ° 2    4n 3 Q 3 f		1 — Q 2
	Q —	3 t
A = 1 — 2^° °	— 2n 2 Q 2 f	1 — Q^ Q J	| +
22        Q 8n 3 Q 3 f,     1 +------ ° | 1--	° t . J,

,

2 Q

® 0 У 2 ,

—

® 0 _y

Q ²

—

® 0 У 1 + ® o e ( t )

B ( Z ) = 2n ² Q 2 Z ^1/3--⁰ ,

10 3 Q

Как и ранее, чтобы подчеркнуть смысл индекса n как дискретного времени в ДВ-системе (13)—(14), вводим новое обозначение y [ n ] = y _n и измеряем частоты в единицах частоты дискретизации: to ° A t = 2nQ ° . Колебания y [ n ], возбуждаемые гармоническим воздействием e [ n ] = EZⁿ ( j Q), представим в виде

y [ n ] = Y Zⁿ ( j Q),                                 (15)

где Y = ( Y 1 , Y 2 ) T — вектор-столбец комплексных амплитуд Y 1 и Y 2 , зависящих от частоты Q. Тогда частотная характеристика ДВ-осциллятора (13)–(14) определяется отношением

H ( j Q) = Yj ).                         (16)

E

После подстановки (15) в (13)–(14) и проведения преобразований получим систему линейных алгебраических уравнений для комплексных амплитуд

B 2 ( Z )

nQ °

3nQ o Z 2/3 _— 2n ² Q 2 Z 1/3 +

2 Q

4n ³ Q 0 <1

3 I

– для RK 4:

A ₁₁

= 1 — 2n ² Q °

—

Q ²

;

4n ³ Q 3   2n ⁴ Q 4 L

+---⁰ + —ЛI 1

3 Q     3 Q ²

—

2n ² Q 2

A 12 = ^{2 nQ} o    —--

Q

4n ³ Q 3 C 1 )  4n ⁴ ° 4 C 1 )

--1--~ +--1--~ .

3 t Q ² J    3 Q  (   2 Q ² J

Q ²

2nQn 991     11

A ₂₂ = 1-- 0 — 2n ² Q 2 1 — — +

²² Q         0 I    Q ² J

8n ³ Q 3 L 1 1  2n ⁴ Q 4 L   3    1 1

+         ⁰ 111+         ⁰ 11+I,

3 Q (   2 Q ² J 3   (    Q ²    Q ⁴ J

ZY 1 = A_n Y 1 + A 12 Y 2 + B 1 ( Z ) E , ZY 2 = A 21 Y 1 + A 22 Y 2 + B 2 ( Z ) E .

B 1 ( Z ) =

< 4n ² Q 2

—

2n 3 Q 0 ¹ 3 Q

Z 1/2

+

Здесь элементы матрицы À и функции B_i ( Z ) зависят от собственной частоты to o и добротности Q НВ-осциллятора (1). Для алгоритмов второ-

2л 2 0 2_ _ 2n ³ Q 0 _ 2n 4 Q g_ <  1 _ 1 I

+   3       3 Q     3 Q ² t    Q ² J ’

го, третьего и четвертого порядков получе-

ны следующие формулы расчета элементов A_ij ( A 21 = — A 12 ) и функций B i ( Z ):

– для RK 2:

B 2 ( z ) = ^0 ° Z +

+

< 4nQ₀

4n ² 0 2

3 Q

2n ³ Q 0

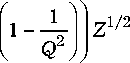
A 11	= 1	— 2n 2 Q ° ,	A 12 = 2nQ0 —	2n 2 Q ° Q
A 22	= 1	2nQ0 Q	2п 2 0 2 I 1 —     1 t    Q 2 J	,

,

+ nQ ° _— 2n ² Q ° _— 2n ³ Q 0 <1 _— Д_

⁺1-   3 Q 3 t Q ²

4n ⁴ 0 4 f,     1 1

+--------- ° I 1-- 3“ I.

^{3 Q}  t   2 Q ² J

B 1 ( Z ) = 2n ² Q ° ,

B ₂( Z ) = nQ₀ Z + nQ₀ I 1

2nQ0 ).

Q ² J’

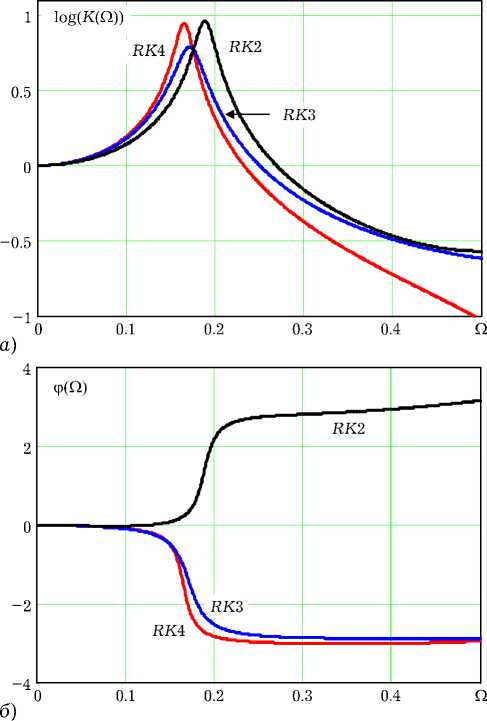
На рис. 3 представлены результаты расчетов амплитудно-частотных (рис. 3, а ) и фазочастотных (рис. 3, б ) характеристик ДВ-осциллято-

e[n] —► T

Рис. 3. АЧХ и ФЧХ ДВ-осцилляторов с алгоритмами Рунге – Кутта

Х2И

У1И

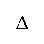
Х1И

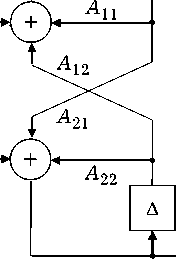
Рис. 4. Блок-схема ДВ-системы (18)

У2И

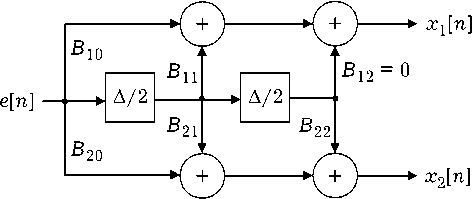
Рис. 5. Блок-схема трансверсальной части ДВ-системы (18)

функций B_i ( Z ). Например, для алгоритма RK 4 она описывается уравнениями:

Х1[n] = Еюe[n] + Bne[n - 1/2], x2[n] = B20e[n] + B21e[n - 1/ 2] + B22e[n - 11>

ров (13)—(14) с параметрами Q0 = 0.167, Q = 10. Расчеты проведены на основе решений СЛАУ (17) с учетом определения (16). Как и следовало ожидать, алгоритм RK4 наиболее точно воспро- изводит частотную характеристику линейного резонатора. А вид фазочастотной характеристи- ки RK2 свидетельствует о неустойчивости чис- ленного

метода при

выбранной величине шага

to₀A t = 2nQ₀ = 1.047.

Переход в СЛАУ (17) к дискретному временному аргументу позволяет получить общий вид разностных уравнений движения ДВ-осциллятора:

У 1 [ n ] = A 11 У 1 [ n - 1] + A 12 У 2 [ n - 1] + X 1 [ n ],

У 2 [ n ] = A 21 У 1 Е n - 1] + A 22 У 2 [ n - 1] + X 2 [n ],

где входные воздействия x ₁[ n ] и x ₂ [ n ] на рекурсивную часть системы формируются трансверсальной подсистемой с повышенной частотой дискретизации. Блок-схема рекурсивной ДВ-системы (18) показана на рис. 4.

Структуру трансверсальной подсистемы нетрудно установить на основе выражений для где полуцелые значения дискретного времени означают, что выборка входного сигнала производится с удвоенной частотой дискретизации. Блок-схема подсистемы (19) изображена на рис. 5.

Отметим, что представления в форме ДВ-систем полезны при исследовании устойчивости численных алгоритмов. Так, основываясь на блок-схемах рис. 4 и рис. 5, можно утверждать, что устойчивость методов Рунге – Кутта при моделировании диссипативных осцилляторов определяется устойчивостью рекурсивной системы (18). А она устойчива при условии, что корни полинома

P ⁽ z ) = ^{1 -} ( ^A 11 ⁺ A 22 ⁺ A 12 A 21 ) z ^{1 + A} 11 A 22 z ² на комплексной плоскости z находятся в круге единичного радиуса и с центром в начале координат. Но, так как коэффициенты A_ij являются функциями частоты Q 0 = K^A t /2п и добротности Q , условие нахождения в единичном круге связывает максимальный шаг интегрирования A t с параметрами осциллятора ® 0 и Q .

Заключение

При анализе погрешностей численных экспериментов по исследованию временных и частотных характеристик нелинейных резонансных систем полезно использовать представления численных алгоритмов в форме динамических систем с дискретным временем. На их основе показано, что импульсно-инвариантный метод (10) за счет однократного, а не четырехкратного вычисления нелинейных функций в уравнениях движения колебательных систем имеет большую вычислительную эффективность, чем близкий ему по точности метод Рунге – Кутта четвертого порядка. Но вычисления по RK4 позволяют более точно определять гармонический состав нелинейных колебаний. Однако наличие в схеме RK4 удвоенной частоты дискретизации затрудняет использование алгоритма в устройствах цифровой обработки сигналов.