О дробном интегродифференцировании Адамара и типа Адамара по направлению в весовых пространствах Лебега со смешанной нормой

Ж. Адамаром (J. Hadamard [1]) была введена конструкция дробного интегродифференцирования, являющаяся дробной степенью (ж^Х) , приспособленная к полуоси и инвариантная относительно растяжения.

В данной работе изучены качественные свойства дробных интегралов и производных Адамара, типа Адамара и типа Маршо — Адамара по направлению в весовых пространствах Лебега со смешанной нормой.

Пространства Лебега со смешанной нормой были введены и изучены в работе [2]. Изучению ограниченности операторов в пространствах Лебега со смешанной нормой посвящены работы [3, 4]. Ряд свойств смешанных пространств Лебега можно найти в [5].

Частные и смешанные дробные производные Маршо в случае двух переменных содержатся уже в работе A. Marchaud [6]. Дробные интегралы и производные по направлению функций многих переменных впервые введены И. А. Киприяновым [7]. В работах [7, 8] изучены различные свойства дробных производных по направлению. В работе [9] изучены качественные свойства оператора дробного дифференцирования в смысле Кипри-янова.

В статьях [10–16] были рассмотрены операторы одномерного дробного интегродифференцирования Адамара и типа Адамара. Ряд свойств дробного интегрирования по Адамару можно найти в книге [17].

В данной работе изучены свойства операторов «типа свертки»: инвариантность относительно растяжения в весовых смешанных пространствах Лебега. Исследованы свойства операторов дробного интегрирования и дифференцирования Адамара и типа Адамара по направлению на R + . Даны условия ограниченности оператора дробного интегрирования Адамара и типа Адамара по направлению в весовом пространстве суммируемых функций на R + , рассмотрены композиции дробного интеграла типа Адамара и дробной производной типа Маршо — Адамара по направлению и получено интегральное представление усеченных дробных производных Маршо — Адамара и типа Маршо — Адамара по направлению. На оснавании интегральных представлений, доказаны теоремы обращения дробных интегралов Адамара и типа Адамара по направлению в весовых пространствах Лебега со смешанной нормой. Кроме того, доказаны связи между обыкновенными и усеченными дробными производными типа Маршо — Адамара по направлению.

Теория дробного дифференцирования в смысле Адамара и Маршо — Адамара развивается также в приложениях к решению интегро-дифференциалных уравнений в обыкновенных и частных производных, интегро-дифферецальные операторы которых принимают нецелые вещественные и комплексные значения, зависят от времени или других аргументов (см., например, [18, 19]).

Рассмотрение ведется в рамках пространств L p,Y = L p,Y (R f , dx), определяемых смешанной нормой

f; ^l p,y II

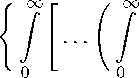
I f (x) | ^p 1 x ^Y 1

p 2

X) X-

pn pn-1

-γ n x _n

dx 1 pn x n ^.

Работа имеет следующую структуру. В разделах 2 и 3 приводятся определения и различные вспомогательные свойства Адамара, типа Адамара и типа Маршо — Адамара по направлению, а в разделе 4 — вспомогательные леммы для пространств L _p,γ . В разделах 5, 6 и 7 содержатся доказательства основных результатов: в разделе 5 доказывается ограниченность дробного интегрирования Адамара и типа Адамара по направлению в пространствах со смешанными нормами; в разделе 6 получены интегральные представления усеченных дробных производных Маршо — Адамара и типа Маршо — Адамара по направлению в весовых смешанных пространствах Лебега, а в разделе 7 доказываются теоремы обращения дробных интегралов Адамара и типа Адамара по направлению от функций из L _p,γ .

Обозначения. N — множество натуральных чисел, R — множество вещественных чисел, C — множество комплексных чисел; Rn — n-мерное евклидово пространство точек x = (xi,..., x"), R" — компактификация R" с одной бесконечно удаленной точ- кой, R+ = {x G Rn; x1 > 0, ..., xn > 0}; E — единичный оператор; (npf) (x) = f (x о p), x,p G R+, — оператор растяжения. Введем конечную разность с использованием оператора растяжения

(А Т f ) (x) = Е ( - 1) k ( k ) f ( xt k ) = (E - П т ) l f,   l G N, т G R ^ ,          (1)

k =0

• (k) — биномиальные коэффициенты. Условимся, что запись 1 ^ p <  то и p = то , где p = (p i ,..., p n ) , то = ( то ,..., то ) , означает, что 1 ^ p i <  то , p i = то , i = 1,..., n . Основные результаты данной работы не будут касаться смешанных пространств L _p,γ ( R + , dX), когда одна часть p i, i = 1,..., n, конечна, а другая часть бесконечна, dx = dx ¹ ... dx n .

X X1 Xn cy (R+) = (f: Ilf; CII = max |x Yf (x)| < то, ^                       X ^ /1 ।

lim x ^Y f (x) |x|> 0

lim x ^Y f |x|→∞

(x)

Y i ^ 0 , i = 1,..., n .

C (R + ) = |f : f G C (R + ) ( a f ( то ) = lim f (x), f (0) = f ( то ) )| . |x|→∞

Пусть w = (w i ,...,w n ) , тогда p ¹ = (p ^{1 1} ,... ,p 1 n ) , x о p ¹ = (x^ ¹ ,... ,x n p ^ n ) , x о t ¹ = (x ₁ t ^{1 1} ,..., x n t ^{1 n} ) , p i > 0 , i = 1,..., n .

={r

u > 0, u < 0.

. J

Y'd

γ i p i ^,

γ i ,

1 < pi < то, pi = то, i = 1,..., n.

Будем использовать К (a, l) = JX t-1-a (1 — e-t)l dt — нормировочные постоянные, известные в теории дробного дифференцирования; CX (R+) — класс бесконечно-дифференцируемых финитных функций с носителем вне начала координат; Г (a, x) = JX e-tta-1dt, a,x G R, — неполная гамма-функция, lim Г (a, x) = Г (a), lim Г (a, x) = 0.

X > 0                       x >x

2.    Дробные интегралы Адамара и типа Адамара по направлению

Дробными интегралами Адамара и типа Адамара порядка a , a G R ^ , по направлению w , w G R + , называем конструкции

i

(J“x)(x) = pX/^n4la-i x (x о x1) d^.

i

(J“,^x)(x) = -1- [^i |lnГ-1 X (x о X1 ш) dl,

,^          Г(a)| где xо|1nш = (x1|1n 11,... ,xn|1nШп) и вектор w = (wi,..., wn) подчинен условию (ln w1)2 + • • • + (ln wn)2 = 1.

Операторы (3), (4) коммутируют с оператором растяжения n p J “ = J “ n p , n p J^ = J “,^ n p и связаны с оператором Римана — Лиувилля I v равенствами

Jy) (x) = (Q-1iaQy) (x), Jlv) (x) = (M-^vQ—^iViQM^vy) (x), где v = In ш = (In Ш1,..., In ^n), (Qy) (x) = у (ex) = у (ex1,..., exn) , (Q-1y) (x) = У (ln x) = у (In xi,..., In xn), (M^vy) (x) = x^v1 .. .xnvn у (xi,...,xn), (M-lvy) (x) = x1 Lv1 ... xnLvnу (xi,..., xn) (см. [17, с. 251] и [10, с. 11]).

Операторы J ^α_,µ и J ^α обладают полугрупповым свойством:

J ', J , ■ = ^+^в У (a > 0, e > 0),                          (5)

J a J e у = J a ^{+ e} у (a > 0, в > 0).                         (6)

Введем модификацию дробного интеграла типа Адамара по направлению с ядром, «улучшенным» на бесконечности. Модификация дробного интеграла типа Адамара по направлению ш , ш € R + имеет вид

∞

J T у) ^(x) = j (^А Т - 1 k^{+ (-)} у (^x ° ^{- 1п ш} ) d—^-,                     ⁽⁷⁾

∞

(^{J a},L ; т у) ^(x) = j (^А Т - 1 k + a ) ^(-) у (^x ° ^{- ln ш} ) d—^-,                       ⁽⁸⁾

где т € R + , у >  0 ,

(Д Т - 1 k + ) (*) = г^ E ( - 1) ^k ( k )(ln ^T) a ¹ - (^А Т - 1 k + ) (t) € L i (R + ) .

(^А Т - 1 ^k + ,a ) («)=Г^а E ( - 1) ^к ( _k ) (a) " (ln T)₊ • (^Д Т - 1 «-1 (^-) € L i ( ^R + ) .

Oчевидно, что α,l         l α α,l            l α

I Ш,т У = Ат I Шу, I Ш;^ ;т У = ДТ I Ш,^У на достаточно хороших функциях y(x), т. е. операторы (7)-(8) получаются применением определения в (1) разностных операторов АТ с «мультипликативным» шагом к операторам Jay и Ja,LV. Они имеют то преимущество по сравнению с Jay, что при l > a > 0 и Ja,^y, они ограничены в пространстве Lp,Y( (R+, dy) при всех 1 ^ pi < то, Yi > 0, i = 1,..., n (т. е. включая случай Yi = 0, i = 1,..., n).

• 3.    Дробное дифференцирование Маршо — Адамара и типа Маршо — Адамара по направлению

Дробной производной Маршо — Адамара порядка a (a € R + ) по направлению ш = (ш 1 ,..., ш _п ) , ш € R + , назовем следующее выражение:

¹         - 1 -a

0,

(^a, i)                 —                                               — построенное с помощью конечной разности, взятой вдоль направления.

Дробные производные Маршо — Адамара D _ω ^α f связаны с дробным призводным Мар-шо D a f равенствам D % f = Q ^—i D a Qf , где v = ln w.

Дробные производные типа Маршо — Адамара D _ω ^α _,µ f связаны с оператором Римана — Лиувилля I _v ^α равенствам

«Усеченной» дробной производной Маршо — Адамара и типа Маршо — Адамара функцией f (x), x G R+, по направлению w, w G R+, назовем выражение p        —1—a

(D ^{W ;i— p f})^(x) = щОД) / (^ln t)      (^A t ^ln " ^f)^(x) 7’ l > ^a > ⁰’

P           - i - a

(D ^a,_w i -P ^f) ^(x) = _Г(₁ ⁰ _a ) j ^ (^ln I)     (^^n - ^f) ^(x) J ⁺ P^{f (x)} ’ ⁰< ^a< ^{1 (9)}

где 0 < p < 1. ««Усеченной» дробной производной Маршо — Адамара и типа Маршо — Адамара по направлению будем понимать предел по норме пространства L _p,γ :

D ^a f = lim D^ f, D ^a f = lim D“ _и f.               (10)

• 4.    Вспомогательные леммы

  Лемма 1. Пространства C 0 f 0 (R+)

  
  

плотно в L p < Y (R + , dp ), 1 <  p <  то , ив C y, ₀ (1R + ),

C y, 0 (iR + ) = p : f (x) = x ^Y g (x) , g (x) G C (1R + )

lim g (x) = |x|^ 0

lim g | x |→∞

(x) = 0 ,

для любых —то < Y i <  TO , i = 1,..., n.

<1 Доказательство леммы осуществляется стандартными средствами. >

Лемма 2. Пусть ^ G L p,Y , 1 С p С то , Y i G R, i = 1,..., n, то справедливо неравенство:

||ПрР; Lp,Y II С ^(р7 ) ||^; Lp,Y II , где nYi np

• *(p"') = пp-(p?'), *‘(pY‘ ) = PYi ’     1 С pi < то’

i =i                              (p i i ’      P i = ^TO’ i = 1’...’n.

Кроме того, оператор растяжения аппроксимирует единичный оператор в пространстве L _p,γ :

lim n |nPp — p; Lp,- II = 0.

p^ i — 0

<1 Равенство (11) устанавливается очевидными заменами переменных. Докажем утверждение (13). Имеем

11Пру - у; Lp,Y|| = || [1 - (^(р7*)) 1] Пру + W*)) 1ПР^ - у; LP,Y где ψ ργ∗ — функция (12). Используя обобщенное неравенство Минковского (см. [5, с. 22]), получим

НЩу - у; L p,Y II ^C || [1 - (^(р ⁷ * )) 1] ^П р У ; L p,Y || ⁺ | (^(р ⁷ * )) 1 ^П Р У

^у; L p,Y

В силу (11) имеем

11ПРу - у; Lp,Y1 C I1 - ^(pY ) | 11у; Lp,Y1 + |ПРд - g; Lp1 , где g (x) := x TPy (x), g (x) G Lp (R+, dXx) при 1 C p < то и g (x) 6 C (R +) при p = to. Утверждение (13) следует из неравенства (14). >

Следующие леммы относятся к операторам «типа свертки», инвариантным относительно растяжения в пространствах Lp,γ . Именно, рассмотрим операторы вида га

(В р у) (x) = j k (t) у (x о p t ) dt,

—га га

^(в _ш у) ^(x) = j 0

a (t) у (x о t ^ш ) dt.

Лемма 3. Пусть у G Lp,Y, 1 C Pi C то, Yi G R, i = 1,..., n. Если га k(p) := j -га

n lk(t)l П (pii )tdt < 'x" i=1

то оператор B _ρ ограничен в пространстве L _p,γ , и

^|В р ^у; L p,Y h ^{C k (p)} ||^у; L p,Y h •

< Так как (Вру) (x) = Гга k (t)(nptу) (x) dt, применив обобщенное неравенство Минковского, получим га

^|В р у; L p,Y h = j ^{|k (t)| | (n} p t у^)(x)

; L p,Y ¹ dt.

-га

В силу равенства (11) получаем (16). >

Следствие 1. Пусть L p,Y , 1 C P C то , Y i G R, i = 1,...,n. Если d (ш) : = J га | a (t) | t ^Y * ^{o ш} dt <  то , где Y * о ш = ^2П =1 Y i ^ i , то оператор В _ш ограничен в пространстве L _p,γ , и

^|В ш ^у; L p,Y ^{1 C d (ш) |у;} L p,Y ^h •

Следствие 2. Пусть в (15) a (t) = 0 при t ^ 1. Тогда оператор (15) ограничен в пространстве L p,Y при всех 1 C P i C то , Y i ^ 0, Ш i ^ 0, i = 1,..., n, если / 1 | a (t) | dt <  + то .

Лемма 4. Пусть k (t) G Li (R), ki (yi) = 0 при t < 0. Тогда "BPys Lp,YII ^ Ilk; Li (R)I 11У; Lp,YII при 0 < pi ^ 1, i = 1,..., n.

Доказательство леммы 4 вытекает из леммы 3.

Лемма 5. Пусть k (t) G L1 (R), k (t) = 0 при t < 0 и J/ k (t) dt = 1. Тогда lim IBpV — у; Lp,YII =0                              (17)

ρ→ 1 - 0

для всех 1 <  p i ^ то , Y i ^ 0, 0 < p i ^ 1, i = 1,..., n.

<1 Прежде всего отметим, что В р У G L p,Y для У G L p,Y при 0 < P i <  1 , i = 1,... ,n , согласно лемме 4. Заметим, что, так как 0 / k (t) dt = 1 , то

∞

(B p P) ^{(x) -} У ^(x)

= У k (t) [(H p t у ) (x) — у (x) ] dt.

Используя обобщенное неравенство Минковского, получим оценку

11^врУ ^— У; ^l p,y II

<

∞ j Ik (t)| ||(nptУ) (x) — У (x); lp,yII 0

dt.

Поскольку 0 < p i ^ 1, i = 1,..., n , то в (18) возможен предельный переход под знаком интеграла на основании мажорантной теоремы Лебега. Применение последней обосновано утверждениями (11), (13) леммы 2. >

5.    Об ограниченности дробного интегрирования по Адамару и типа Адамара в пространстве Lp,γ

Теорема 1. Пусть Y i G R, 1 <  p i < то , a i > 0 и у G C. Если Re у + ^2П =1 Y i* 1” ^w i > 0, то оператор J _ω ^α _,µ ограничен в L _p,γ и

J ,^ ^l p,y II ^ Q p ^{Iy; l} p,y h ,                            ⁽¹⁹⁾

где Q µ

=

n

Re У + Z Y* ln ^i i=1

)

α

< Сначала рассмотрим случай 1 ^ p <  то . С помощью обобщенного неравенства Минковского, получаем

∞

I J a» v; L p,y I <  J IY ,« (y)l | y (x ◦ y ln " ) S L p,y I dyy.

После подстановки T i = x i y ^{ln Ш i} , i = 1,..., n , имеем

1 n

1 Г p + ^ ^Yi In ^ i                          /77/

| J a,p ^s L p,y I <  ^ J y   i- pi     l iny l ^{a -1} I y; L p,y I у

< rT^/e - ^P+ ^ * ^Yi l" ' " У; L p- I <  f ^ + i^ ^Y- 1”" ')

^{r (a)} J                                           \ Pi )

₀                                                     i =1

α

^{Iy; L} p,y h .

В случае p = то в (20) заменим p i, i = 1,..., n на 1. Тогда получим (19). >

Теорема 2. 1) Пусть Y i Е R, 1 C p i C то , a i > 0, i = 1,..., n. Если ЕП =1 Y * ln w _t > 0, то оператор J _ω ^α ограничен в L _p,γ и

IIJ VS LP,YII C Q0 IIV; LPYII , где Qo = (En=i Y* In Wi)-“ .

• 2) Пусть 1 C p t C то , 1 C q t C то , 0 < a t <  1, i = 1,... ,n. Оператор J - v дробного интегрирования ограничен из L _p R ⁿ ₊ , ^d _x ^x в L _q R ⁿ ₊ , ^d _x ^x тогда и только тогда, когда ¹

  t <  - 1 - , q t = i -p i- p i , i = i,...,n.

• <1 Первое утверждение вытекает из теоремы 1. Далее, оператор J — V связан с оператором Римана — Лиувилля I _v ^α ϕ равенством

Jv = Q — 1 I - Qv,                           (21)

где ( Qv ) (x) = V (e x ) = V (e x ¹ , • • •, e x n ) , v = ln w . В силу (21) второе утверждение теоремы следует из известной теоремы Харди — Литтлвуда для обычного дробного интегрирования по R ⁿ (см. [17, c. 345]). >

Теорема 3. Операторы J ^α,^,µ^l ,τ и J ^α,^,τ^l ограничены в пространстве L _p,γ при всех 1 C P t C то , i = 1,..., n,

||j“.",tVS LPY II C c (т,Д) II VS Lp,YII , где 0 < c (т, д) < 1 при Re д + ЕП=1 Y* ln wt ^ 0, 0 < т C 1, l > a > 0,

|Jw,’tv; Lp.Y || C ci (т) IIV; Lp,Y1 , где 0 < c1 (т) < 1 при ^n=1 Y* ln wt ^ 0, 0 < т C 1, l > a > 0.

• < Доказательство этой теоремы вытекает из следствия 2 леммы 3. >

Теорема 4. Пусть a >  0, в > 0, 1 C P t C то , Y t Е R, i = 1,..., n, и д Е C.

• 1)    Если Re д >  — ЕП =1 Y * ln w t , то оператор J -," обладает полугрупповым свойством (5) в пространстве L p_,γ .

• 2)    Если ЕП =1 Y * ln w t > 0, то оператор J J обладает полугрупповым свойством (6) в пространстве L p_,γ .

• <    Сначала равенство (5) докажем для «достаточно хороших» функций V . Поменяв порядок интегрирования по формуле Дирихле, придем к равенству

( ^JY^J e.V (x) = 5^1^)/4 " Un4 I “ ^-1 d^f^j /т " | inT | ^{e -i} V (x ◦ (4т) ^ln “ ) dr 00

• ^{1                       1}                  В- 1

• ¹          u h™A du fl, "- -! , u     d⁴

= Г (a) Г (в) 7 ^u4x ° u hr /^{|ln 41 ln} 4 У

Внутренний интеграл легко вычисляется после замены ln 4 = ln u ln y :

1 e

(JJ " V)(x) =      1      /"u " | ln u |-" ^e V (x ° u ^ln “ ) du [ | ln y | " ^-1 (1 — ln y) ^{e -1} dy

1 ^(a) 1 ^(e) J                        u          ' U- J                               ^y

• = riaEi / u"^|lnu|“^+e-1V (x ° u^h™) du = J:^evxx).

6. Интегральное представление усеченных дробных производных Маршо — Адамара и типа Маршо — Адамара по направлению

Отсюда получаем равенство (5) для «достаточно хороших» функций ϕ .

Если Re p >  — ^ П ₌₁ Y * ln w i , то в силу теоремы 1 операторы J ),^ , J ).^ и J^P ограничены в L p,Y, и равенство (5) верно для v G L p- .

Когда p = 0 , из теоремы 4 и теоремы 2 получаем полугрупповое свойство операторов дробного интегрирования Адамара (3). >

Всюду ниже вектор p = (p i ,... ,p _n ) либо имеет все конечные компоненты p i (p <  то ) , либо все бесконечные p = то = ( то ,..., то ) .

Лемма 6. Пусть f(x) = (J O^ v) (x), V G L p,Y , где 0 < a <  1, p >  0, 1 <  p i <  то , Y i , ln w i G R, i = 1,..., n, p + 52П =1 p i ln w i > 0 и 0 <  p <  1. Тогда усеченная дробная производная типа Маршо — Адамара D a p. -1 —p f по направлению W, имеет следующее интегральное представление:

∞

D^- p f = JK^ (t, p) V (x ◦ p t ^{ln )} ) dt,                  (22)

где

K + ,_M ^(t, P)

sin an p ^t πt

0^ аГ ^ — a, p In -^ + Г (1 — a)^ ^p In -^ (t) + — (t — 1) +

При этом ядро K_<41 (t, p) G L i (R^) является усредняющим

∞

IK^ (t,p) dt = 1,   K^ (t,p) > 0,                      (24)

при t > 0 .

<1 Из (8) при 0 < t <  1 , l = 1 имеем

∞ f (x) — f (x ◦ tln )) = fln1) T~a / t^y ya-1v(x o t    Г (a)

t y ^ln ^ dy

∞

— j t ^ ^{( y - 1}^( y — 1) ^{a -i} v(x о t y ^{ln )} i

) dy^.

Поэтому

∞ f (x) — f (xt)=(ln-t) y"k+^(y,t)y(x о tyln)) dy,                  (25)

где x о t y ^{ln )} = (x i t y ^{ln ) 1} ,...,x n t ^{y ln )} n) ,

^k + ,^ ^(y,t)   r(a)

Г t ^y y ^{a -i} ,

(t ^yy y ^{a -i} — t ^{y ( y -1)} (y — 1) ^{a -i} ,

0 1, y > 1.

Известно, что k + ,^ (y,t) € L i (R + ) и Jq ° ^k + ,_P ⁽y ^{,t ) d} y = ⁰ (см. [12]). Из (25) получаем

ρ∞

D “,_M ;1 -p f = _Г(₁ — _а ) j 1ПТ t^ У k+MW ° t y ln ^Ш ) dy ⁺ ^ “ f ⁽x). 0 t 0

Замены ln 1 = ? и y? = т дают

∞∞

D^ -p f = _r(1 ^Q _ _{a )} / = "* d? J k + _# (^e ^{- <}) ^x ° e ^{- T} ‘° " ^{W +} ^f ^M '    (26)

ln 1            0

ρ

Перестановка порядка интегрирования в правой части в (26) приводит к равенству

α

^w , ц -1 — p J

α

Г(1 - a)

t/ ln ¹

∞p у ^(x ° e-T ln w)    у e-

s ^{T k} + _д (^s,e s) ds ⁺ ц “ У ^(x)

∞

Г(а)Г(1 — a) I J

x ° p t ^{ln w}

—a, ц In —^ + Г(1 — a) j

x (ц In ¹) “ p^dt — J p ^t (t — 1) ^a _V (x ° p t ^{ln w} ) d-V p ₁

что совпадает с (22).

Утверждения (23)-(24) для функции K + ^ (t, p) известны (см. [12]). Остается обосновать действия в (27). Для ^ € C Q^ 'R ^ ) они очевидны и, следовательно, для таких функций тождество (22) доказано. В силу леммы 4 и теоремы 1 оператор D ^ ^ -i -p J ^^ , стоящий в левой части тождества (22), ограничен в L p^ при ц + ^2П =1 p i ln W i > 0 . Ограничен и оператор в правой части в силу той же леммы 4. Поэтому на основании леммы 1 тождество (22) распространяется с C Q^O (R +) на все функции у € L p^ , 1 С P i <  го , i = 1,... ,n, ц + ^ ⁿ =₁ P i ln W i > 0 . ▻

Лемма 7. Пусть f (x) = (J a ^)(x), ^ € L p,Y , где a >  0, 1 С P i С го , Y i , lnw i € R, i = 1,..., n, 52П =₁ Y i* ln w i > 0 или 0 < a <  1, 1 < p i <  a , Y i = 0, i = 1,..., n, и 0 < p <  1. Тогда усеченная дробная производная Маршо — Адамара D ^ 1 -p f по направлению w имеет следующее интегральное представление:

ОО

(Da^-Pf) (x) = У K^(y)^(x ° pylnw) dy,(28)

где

111 ( — 1)k ( k ) (y — k) +

K'+'y) = k=0 «(a,l)r(1 + a)y     € L1 R1

и oo

У K1a(y)dy = 1, l > a > 0.

• <1 Доказательство леммы 7 аналогично доказательству леммы 6. ▻

Замечание. Можно показать, что утверждение леммы справедливо и при Y i = 0 , P i = 1 , i = 1,..., n , 0 < a < 1 , однако это потребует иного обоснования (см. доказательство леммы 8).

Лемма 8. Пусть f G L r\ , 1 С r i С го , A i ^ 0, i = 1,..., n, такова, что ее разность ( △ T f) (x) порядка l, l >  a, представима модифицированным адамаравским дробным интегралом (7) по направлению от функции из L _p,γ :

∞

^(д т f ) ⁽x) = J aT v = j (^д т - i k + )^(t) v (x ° t ^{in ш} ) p

где l > a >  0, 0 < т < 1, v G L p_JY , 1 С P i С го , Y i ^ 0, i = 1,..., n и 0 < p <  1. Тогда усеченная дробная производная D _ω ^α _{, 1 - ρ} f по направлению ω , допускает интегральное представление (28) при всех 1 С P i <  го , Y i ^ 0, i = 1,..., n, и интегральное представление

∞

№- „ /) (x) = У K + (t) v (x ° p t ln " ) dt - v (0)               (32)

при всех P i = го , Y i = 0 , i = 1, . . . , n .

• <1 Так как при Y i > 0 , i = 1,..., n , утверждения леммы 8 обоснованы при доказательстве леммы 6, то рассматриваем случай Y i = 0 , i = 1,... ,n , но при любых a >  0 , 1 С P i С го , i = 1,..., n . Нужно обосновать следующее равенство:

∞∞           ∞      ∞

• / | / ^k + (j) v(x ° e ^{- T} ln “ ) dT = У v(x ° e ^{- T ln} “ ) dT J k+ (|) |.

ln ^{1        0                                                0}                             ln ¹

ρρ

Оно несложно обосновывается теоремой Фубини при 1 С P i <  го , Y i = 0 , i = 1,..., n . Действительно, покажем, что при 1 С P i <  го , Y i = 0 , i = 1,..., n сходится (почти для всех x ) повторный интеграл

∞∞

• У^ ° e —^T ln " )^|dj У k + a (j) ⁰                               ln ¹

ρ для всех v G Lp,о, 1 С P < го. Отсюда замены т = s и т = t ln Р приводят к необходимости доказать сходимость интеграла

∞

J := j |v ⁽ x ° p ^{- t} ln ^{ш )}| k * (t) dt,                             (33)

где K * (t) = 1 Jt |k + _a (s)| ds . Так как k + _a (s) G L i (R + ) , то K * (t) С c при t ^ + го . Далее, очевидно, что K * (t) С ct ^{a -1} при t ^ 0 и что K * (t) непрерывна при 0 < t <  го . Тогда из (33) имеем

1 ∞

J С c У |v(x ° P-tlnш) |ta-i dt + c У |v(x ° P-tlnш) |p и остается сослаться на теорему Юнга для пространств со смешанной нормой (см. [5, с. 25]).

Остается обосновать случай p i = то , i = 1,..., n , когда ^ G C ^R + ). В этом случае, чтобы преодолеть трудности, связанные со вторым слагаемым, т. е. t >  1 , рассмотрим «двустороннее» усечение дробной производной Маршо — Адамара по направлению ω , т. е.

ρ

- 1 -α

(^D 2, i -p,_e f ^{) (x)} = К7О77Г / (ⁱⁿ t)      (^A t in " f)^(x) J, l > ^a > °,

ε где ° < E < p < 1, и затем устремим e ^ °. Согласно (31) и (34) имеем

^ρ       - 1     ^∞

D^-f ) (x)=x / (ln t)   dt J k + y ^ (x ◦ t y ln “) dy

ε

Замены In | = £ и y^ = т дают

(D ^ i - p f (x) =

К (a,l)

∞

7 4

x о e

-

ln 1 ε тln“) dT / k+ (f)df■ ln 1 ρ

Здесь перестановка порядка интегрирования легко обосновывается за счет E > ° (с учетом того, что |у (x)| < c и J^ d^ J0” |k+a(T)|dT < то). Из (35) имеем nρ

∞

(D “ 1 oof ) (x) = [ ^(x о e ^{- T} ln ^a ) — 7— K + — 7— + K + f — 7—) dT.

V ^, ^{1- p}, _ej/vy                   q in p l,^a     in p) in e l ^a\ ln e)

Таким образом,

∞∞

DW ) (x) = j K+ (t) v(x о p ln " ) dt - / Ka (t) v(x о E* ln " ) dt.     (36)

Так как ^ G C (R+) и K + _a (t) G L i (R+) , то во втором слагаемом возможен предельный переход при E ^ ° под знаком интеграла. В силу (30) и (36) получаем интегральное представление (32). >

Рассмотрим функцию

∞

a ( p ^):= j^-^+a (t,P)^dt = (y-7) ” ⁺ гй^ - 0) 0

X

г

— a, ^in -^ρ

)(7—7) ^{— г}(^{— a} ’ ^{— c)ln}p)]'

где K + a (t,p) — функция (23), ° < a <  1 , ° < p <  1 , 7 >  ° , c := — ^7 =1 Y i in^ i, Y i , in w i G R , 7 > c .

Лемма 9. Пусть ° < a < 1, 7 ^ °, c G R, 7 > c и ° < p < 1. Тогда A(p')-функция обладает следующими свойствами:

• 1)    A(p)-функция монотонно убывает при c <  ° и монотонно возрастает при c >  °.

• 2)    Справедливо равенство lim p> i - g A (р) = 1, lim p> o+o A (р) = (^ — с) •

• 3)    Справедливо неравенство (^— с) < А (р) С 1, при c <  0, 1 С А (р) <  (р— с) при 0 < c < ц.

• <1 Найдем производную

7. Обращение дробных интегралов по направлению от функций из Lp,γ

A' ^(р)   Г(1 р - а)^!^ ^{1 (р} -^{С 1).}

Отсюда вытекает утверждение 1), т. е. А (р) < 0 при c < 0 , А (р) > 0 при c > 0.

В силу свойства (2) неполной гамма-функции получим утверждение 2):

lim А (р) = (У + ^ГС-О» [(Л-Г - 11 =1,  lim А (р) = (V p^i-o        Уц — е)    Г(1 — а) [\ц — c)     ] p >0-0        Уц — е)

Утверждение 3) вытекает из утверждения 2) и в силу свойства (2) неполной гамма-функции. >

Теорема 5. Пусть f = J^V, V Е L p,Y , где 0 < а < 1, ц ^ 0, 1 С p i <  то , Y i , ln w i Е R, i = 1,..., n, ц + ^ П ₌₁ p i ln w i > 0 и 0 < р <  1. Тогда

(Da^f) (x) = pJ>"1-0(Da,p;1 —pf) (x) = V (x) , где предел понимается как в Lp,γ .

• <    Сходимость по норме следует из леммы 6 и леммы 5. >

Теорема 6. Пусть f = Л “ ф, V Е L p,Y , где а > 0, 1 С p i С то , Y i , ln w i Е R, i = 1,.. •, n, 52 П =₁ Y i* ln w i > 0 или 0 < а < 1, 1 < p i <  S , Y i = 0, i = 1,..., n, и 0 < р <  1. Тогда

(Daf)(x) = lim(Dai-pf)(x) = V(x), p>i     ’ p где предел понимается как в Lp,γ, так и почти всюду.

• <    Сходимость по норме следует из леммы 7 и леммы 5. Доказательство сходимости почти всюду получим из [20, теорема 2, с. 77–78]. При этом учитываем равенство (29) и свойство ядра \K - _a (t) | С (₁₊у +1 -а при t >  1 (см. [17, с. 379]), так что ядро K - _a (t) имеет монотонную суммируемую мажоранту. >

Теорема 7. Пусть (2\ Т f ) (x) = J^V, V Е L p,Y , где l > а >  0, 0 < т <  1, 1 С p i С то , Y i , ln w i Е R, i = 1,..., n, ^ П =₁ Y * ln w i >  0 и 0 < р < 1. Тогда

(Daf)(x) = lim(Da,i-pf)(x) = V (x) , p>1       r где предел понимается как в Lp,γ, так и почти всюду.

• <    Доказательство теоремы сходимости по норме следует из леммы 8 и леммы 5.

Доказательство сходимости почти всюду — как в теореме 6. >

Из леммы 6 теоремы 5 вытекает связь между нормами дробных производных по направлению ω (9) и (10) в пространств L p_,γ .

Теорема 8. Hycmbf (x) = (J “,^ y) (x), V € L p,Y , где 0 < a <  1, 1 <  p <  to , ^ >  0, c := — ^ Г =₁ pp i In w i , c € R, ^ > c и 0 < p <  1. Тогда

II D .p. 1 -p f ; L pYII <  M \\ ; L p,- II •

M =

,

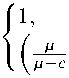
c <  0, c >  0.

• <    Используя (22), применяя обобщенное неравенство Минковского и учитывая (38), имеем

∞ hDa,i-pf; Lp,Yh < I № (t,p)|h^ (x ° ptln"; Lp,Y) h dt < A (p) Kf 5 Lp,Yh , 0

где A(p ) — функция (37). В силу леммы 9 вытекает (39). >

Следствие 3. Пусть f (xt) = (Ja^) (x), V € Lp,Y, где 0 < a < 1, 1 < p < to, c := — ^П=1 pi lnui, c € R, c < 0 и 0 < p < 1. Тогда hDa, 1-pf; Lp,Yh < hD^f; Lp,Yh .