О двух краевых задачах для смешанных уравнений с перпендикулярными линиями изменения типа

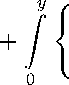
exp ([4(р - р)] ‘)

Ля " Ч)

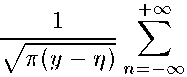
exp

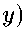
М(у)^У

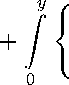
1          00         /         9    \               1                  /i \

1      \- / » \ .         1             /1 \

, .    , > .ехР -",----г + —^=— ехР --,г

^(У " ^ n=i V ^"^)  ^^у-у}   \ (У -У))

1        ,        1        ,             ( (1 + 2п)2\

4--,         4--,         + / ^ехР--;-----г^- ГЛ vl) Ал

2V^(y- У) 2Ул(у - у) п=_оо \ (У - У) / где

у 1

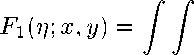
ч о

У 1

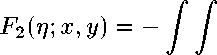
ч о

F3№

Эх

Эх

Ж = 1

FMul

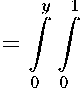
FtoMRtoX.x^Wdt,

Е^.^Гои.О;»,,^^^

О

Рассматривая полученное соотношение между т^ и ^ совместно с (12) и условиями сопряжения (6), приходим к интегральному уравнению Воль-терра второго рода относительно v^ (у)

У viW+ [sto, tHWt = m.

о где ядро StoH и правая части Т(д) выражаются через известные функции. После определения v^^ и т^^ находим решение задачи в области О2 как решение задачи Коши д(1, g) = toYu,.to^ = ^ to) Уравнения (1), а в П„ -как решение первой краевой задачи.

Рассмотрим теперь уравнение

"га ■ Bfi°' u„ - u„ - A?signg/u, в 12,,

где Ш,^ - заданная функция, А, = const (, = 1,2) а П - ™ же область что и в задаче 1. Сохраним и введенные ранее обозначения т, Ь), „, Ь), т₂ („). ^2 (У)'                                                             ____

Задача 2. Найти регулярное в областях Q^ (г = 0,2) решение уравнения (17), удовлетворяющее краевым условиям (3), условиям

=Ub(0,i,)-6Dj„u(0,i,) = V1(i,),

Цое ⁼ ^^ж\ 0 ^ ж

и условиям сопряжения (5), (6), где /)/у — оператор дробного дифференцирования в смысле Римана - Лиувилля [6, с. 28], причем а = а№. Ь = W -заданные непрерывные коэффициенты такие, что ab>0; 6М (т^ДеС^М, «М ЗМ 7z(d, УД2,з(г) G С2[0,1],

Кроме того,

«HDAd) > О, aWi^ + ^d^d) ^ 0, Д(ж)ф(ж) ^ 0.(20)

Под регулярным решением уравнения (17) будем понимать функцию Дх, у) из класса C(QJ П С¹ (По U О A U АС) П С¹ (Qi U О А) П (П₂ АС), а при х = 0 и у G (0,1] удовлетворяющую условию Гельдера с показателем К > 1/2.

Докажем вначале единственность решения задачи 2. Пусть Дх,у) — решение однородной задачи 2. Тогда справедливо равенство 11

[к2 (ж, 1) — к2 (ж, 0)] Ах + I иД,у)ихД,у) dy оо

дмцм^р p.d^». О                      Qn

Так как рассматривается однородная задача, то (18) можно записать в виде

«ао,^ = ю*,и(о,«у

С учетом последнего равенства и принципа экстремума для операторов дробного дифференцирования [7, с. 308], легко убедиться в справедливости неравенства

1 I^^MddSQ. О

Теперь покажем, что Дх, 0) = 0. Для этого в (17) перейдем к пределу при у —> 0+, получим

№)]"-7Ц) = о, откуда, с учетом однородных граничных условий (3), (19) заключаем, что

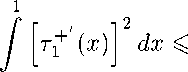
(тМ№=к(#,+(<б = оо

Используя соотношение между тГ (т) и „? (т) можно показать сиранедли-вость неравенства

Л 5 о.(23)

Действительно, удовлетворяя решение задачи Коши _и(т 0) = т_ГЬ), ^иМ 0) = v_x (ж) для уравнения (17) в области Q_x условию (19), будем иметь

П (ж) +

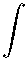
уП ^^1о [^ilV^^ - О] dt t dx LJ

/ X \       I Г /-----------

", w »■

= 2уз ( ~ J + Io Ai | \/t(x — £)

\ 2 / J L 0

Применяя к (24) формулы взаимного обращения интегральных уравнений Вольтерра [8, с. 1138]:

MW-I„ Д*Д « = NW,

Ut L               J

f т й Г /-----------

NW + N(t) J_o V^WW » = MWl, J          d x    L             J

о

получим

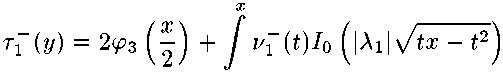
dt

- 2

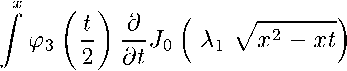
dt

о

Далее, используя равенство

Ж

I₀ f Al                f Al V®² - dt

\                / ot \                 /

= 10 ( Ai V^-^2) - Jo[|Ai|($-O], будем иметь

Ч (ж) = 2<^з

пр 2    гр 4- •aj          «аа V

о

X dt+j v^ (t) Jo [|А1|(ж - £)] dt. о

Подставляя последнее равенство в интеграл г ЛЮДИ J аДгф/ЗДж) о

Д(ж) [аДж)

а также, учитывая однородность условий, получим

1                        х                                      12

• 11    = Г 1 dx I ^WJo^M^-t^dt- /dx.

J аДД/ЗДж)                           Д(ж) |_а1(жД

0                        0о

Используя интегральное представление функции Бесселя Jo [|Ai|(ж — Д], будем иметь

• 1                z                        z 1X 2

1 Г ds f     1      / ГV

• ¹¹    =5?/ 7Г=71^й)ла) [Д ^1,1 ^'^x^^dt)

  -1о

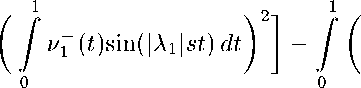
^1 (ФНА^П

ац(ж)/31(ж)

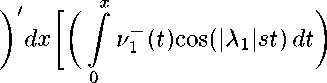
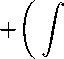
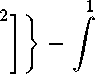
жи² 31(х) [«1(ж)

dx.

Отсюда, принимая =о внимание (20), убеждаемся н справедливости „ера-веиства (23) и, с учетом (22) и (6) заключаем, что т, . = «Ь, 0±) = 0

Далее, замечая, что в области Q2 уравнения (1) и (17) совпадают, на основе полученного ранее неравенства (13) убеждаемся в том, что третье слагаемое в (21) неположительно.

Таким образом, доказана следующая

Теорема 2. В области Q не может существовать более одного решения задачи 2, если выполнены условия (7) и (20).

Рассмотрим теперь вопрос существования решения задачи 2. Первое функциональное соотношение между тГ(т) и „? ^ имеет вид (24). Переходя к пределу при у —> 0+ в (17) и используя условия сопряжения, получим второе функциональное соотношение между rf^) и щ (ж)

vx ^ = 3^)1

Н^ЛУ _+№,0) +ФМ

°^

И (я) - 71 (^ж) _а1(_Ж)

+ <71(ж).

Разрешая систему уравнений (24), (25) относительно тЩ) приходим к интегральному уравнению Вольтерра второго рода

Ж т?ЬН [KMtWMdt^^Y

О где

«1(Щ5о(фг) Г

t

ai(t)

-S^H2!;

+ а)Щ

61W + ^(^

2Ki«-«i^MWl

SoKn)A^)^W

—77 - 2 ^ад^)

«iW

3iW

d2 8t2

"W)

№y№№i

«1(0)

“i^L

о

о

~ 7i(*) ~

_од(3)

7iU35i(t)

ai(t)cri(t) 3i(t)

> (It /

о

So(^t) — Iq ^ Ai i/#(^ - i)^ , Si(^H) — |g£^o ^ Ai \/i(C - £)) ,

Г|ж) " / A(t) *'

Заметим, что правая часть равенства (26) зависит от тГ (0). Для нахождения этого числа обратим интегральное уравнение (26). Получим

Ж

^“(ж) = Ф1(ж) — I Ri(x, t^i(t)dt,                 (27)

о где Ri(x, t) — резольвента ядра Ki^x, t).

Положив в (27) х = 1, в результате элементарных преобразований получим

Tf'(0)

-1 ^2

ллми кзим».

о где

— , х , , х \ /31(0)Т(ж) Ф1(ж) = ФЦж) - Ту (0), аЦО)

Л = ^ [тд - [ТТТ Д1(1,0^ 01(0) L 3 ЛОТ 3

О

Таким образом, равенство (27) дает решение задачи 2 в области Qi, при условии, что J^ RTlT)dE, ф 1. Как известно [9, с. 1290], общее решение урав-„ения (17) в области П_о, удовлетворяющее условию „(щ, 0+) = тДт), имеет вид:

«(ж,у) =

У

1 г

о

У

1 L

• 1      / ж

• ²    ехр --------

• V 4(y-t)

«х(0.0-Д7—7Т'‘<°-() »

i / (ж — I)2 2 ехр --------

V 4(у-^)

о

• 1    Г 1      / (ж — Н²

• -^ / — ехр-----

• v^ J Ту V 4У о

• 1    У

х — 1

«шл - ₂^_^“(Г*) 31

t^W

• 1     / т - Т²\

• ²    ехр --------- dt.

о о

В силу того, что [10, с. 1291]

„ X                    з .     .                          \1

lim —— (у — t) ² u(0, t) exp — —----- dt = -u^

^0+4^ J V             V 4(y-t)V2

о

у

1 - X                       ( (x - 1)2\ „1

lim -- — Mb — t) ² u 1, t) exp —------ dt = -u

J               \ Цу-t)) 2

о переходя к пределу в (28) при х —> 0+ и при х —> 1— соответственно, будем иметь у у

ЦЦЦ

dq _№м._я-М^-^—Л» О о

У

+ Т= / Ц - ^ ^ехР \/7Г J

Цу-ty) ^^^ 2(у-^1,1\ dt

О

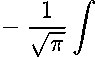
У

Ц - ^"^и_ж(0, t)dt +

о

у

1 Г 1 а

/ ^ехр

J Цу о

. if,            / I П          «(0,t) 1 ,.

u(l, у) =--= Му — t) 2 exp--------- иж(0, t)-------- dt

V Цу-t)) ^; 2(y-£)J о

+ -7= МУ-t) 2МЖ(1,^)^ + —= -^=exp--—— T+(t)dt оо у у

+    [ d^ [ f^,t)(y-t)~^ expdt.

J J              \ Цу-н)

о о

Отсюда, с учетом (12), (18), условий сопряжения (5), (6), получаем интегральное уравнение Вольтерра первого рода

у

LtWH^.tW-HM.            (29)

О

Здесь ядро НМЛ и правая часть Н2(р) выражаются через известные фуик-дни. В силу того, что Я1(р,,) / 0, уравнение (29) легко сводиться к интегральному уравнению Вольтерра второго рода [10, с. 149]. После определения v^y^ и т^^ находим решение задачи 2 в областях Q12 как решение задач Коши, ав Qq — как решение первой краевой задачи.