О двух модификациях метода наименьших квадратов в задаче восстановления утерянной информации системы видеоанализа по показаниям акселерометра

Клинический анализ движений человека в последние годы получил признание как один из наиболее эффективных методов диагностики различных видов патологии опорно-двигательного аппарата [3, 15]. Это обусловлено относительной доступностью аппаратуры и возможностью изучать достаточно «чистое» движение (в отличие от контактных датчиков, которые могут оказывать существенное влияние на ход обследования). Однако при использовании систем этого типа может возникать ряд технических трудностей. Например, в процессе движения в течение некоторого промежутка времени один из светоотражателей может быть закрыт от объектива камеры. Соответственно, на этом промежутке невозможно получить значение одного или нескольких углов. Ранее для решения этой задачи обычно применялись методы сплайновой аппроксимации либо коррекция показаний по информации о длине звена антропоморфного многозвенника [13]. Однако первый способ использует только информацию о гладкости траекторий, а второй имеет большую погрешность из-за изменения расстояния между маркерами. Для устранения данного недостатка системы видеоанализа предполагается использовать показания различных датчиков, измерения

Бобылев Алексей Николаевич, аспирант каф. прикладной механики и управления МГУ, Москва Болотин Юрий Владимирович, д.ф.-м.н., проф. каф. прикладной механики и управления МГУ, Москва Воронов Андрей Владимирович, д.б.н., в.н.с., Институт медико-биологических проблем РАН, Москва Кручинин Павел Анатольевич, к.ф.-м.н., доцент каф. прикладной механики и управления МГУ, Москва которых основаны на других принципах работы [5]. В исследованиях [5–7] рассматривалась задача о восстановлении пропавших показаний при видеоанализе с использованием измерений стабилографической платформы. Для решения авторам потребовалось записывать сложные динамические уравнения, учитывая значительное количество неизвестных параметров, и существенно ограничить класс допустимых движений. В настоящий момент доступность для применения различных измерительных приборов сделала возможным поставить ту же задачу с использованием других датчиков.

В работе [2] описан способ восстановления показаний системы видеоанализа по дополнительным измерениям двухкомпонентного датчика линейных ускорений – акселерометра. Настоящая работа посвящена подробной разработке алгоритмов решения этой задачи для случая плоского движения. Исследуется движение одного из звеньев человека, например, бедра или голени. В качестве измерений системы видеоанализа рассматривается угол, образованный звеном с горизонталью, вычисленный по показаниям системы видеоанализа. Моделируется ситуация, когда на некотором интервале времени значения угла считаются утерянными.

Описание измерительных систем

Рассмотрим процедуру анализа видеоизображений движения человека. Движения человека регистрируются при помощи видеокамер. На характерные точки тела человека наносятся маркеры, по изображению которых определяются координаты точек тела. Все измерения координат записываются компьютером, после чего исследователь проводит анализ полученных траекторий или характерных углов, вычисленных по этим координатам. Движение человека не затруднено какими-либо массивными датчиками или проводами, которые часто мешают проводить полноценные исследования, например, с пациентами, у которых нарушен опорнодвигательный аппарат или имеются какие-либо неврологические заболевания.

В настоящей работе рассматривается система видеоанализа, использующая видеопоток с одной видеокамеры.

Для решения проблем сбоев видеосистемы предлагается применять дополнительные измерения акселерометра. Выбор данного прибора обусловлен несколькими факторами. Во-первых, на сегодняшний день акселерометр доступен для проведения лабораторных испытаний. Во-вторых, этот датчик, выполненный с использованием технологий MEMS и Bluetooth , почти не ограничивает движение. В-третьих, использование показаний акселерометра не требует введения в модель динамических уравнений движения тела человека в целом и позволяет ограничиться кинематическими соотношениями для одного сегмента.

Измерениями двухкомпонентного акселерометра являются проекции на две ортогональные оси удельной силы, действующей на чувствительную массу. Измерительный прибор представляет собой легкий малогабаритный датчик в жестком корпусе. Крепление акселерометра производится непосредственно на поверхность тела в зоне наименьшей подвижности кожного покрова (рис. 1).

Уравнения движения звена

Решаем задачу о движении звена в плоскости. Будем рассматривать модель одного из звеньев конечности человеческого тела (предплечья, плеча, голени или бедра).

Считаем рассматриваемый объект твердым телом, совершающим непрерывное плоскопараллельное движение. Будем исследовать плоские движения отрезка, соединяющего две фиксированные точки O 1 и O 2 на теле. Положение отрезка однозначно задает положение звена (рис. 2).

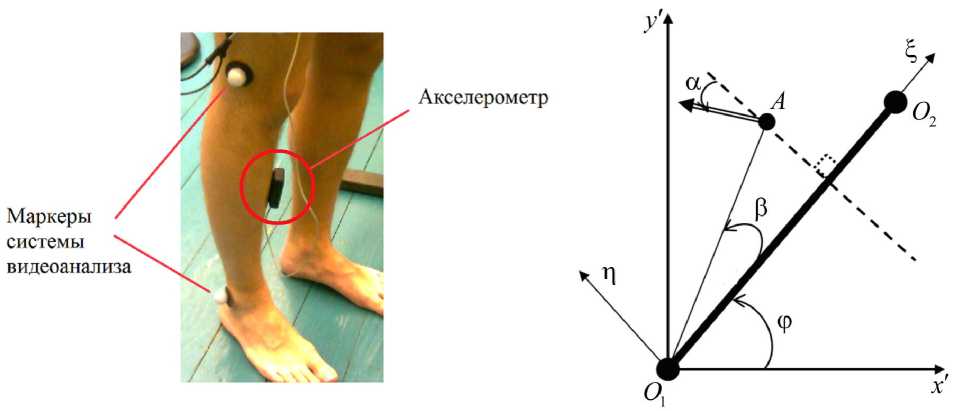
Рис. 1. Крепление акселерометра

Рис. 2. Модель звена конечности

В качестве точек O 1 и O 2 выберем точки крепления маркеров на концах звена. Место крепления и ориентация датчика ускорений в общем случае неизвестны.

Обозначим через A центр чувствительной массы акселерометра. Зададим положение точки A расстоянием l от O 1 и углом β между отрезками O 1 O 2 и O 1 A .

Рассмотрим одну из двух осей чувствительности акселерометра. Ориентацию оси зададим углом α её отклонения от перпендикуляра к O 1 O 2 . Длина l и углы α и β – неизвестные параметры системы. Выражение для проекции ускорения точки A на ось чувствительности акселерометра запишем из теоремы о сложении ускорений при плоскопараллельном движении [10]

а_а = 1 sin( a - Р ) ф ² + 1 cos( a - Р ) ф + sin a ( - X 1 cos ф- _ y 1 sin ф ) + cos a ( - X 1 sin ф + y 1 cos ф ). (1)

Показания акселерометра по выбранной оси в силу конструкции не совпадают с величинами ускорений a_a . Хотя схема работы современных акселерометров и сложна с технической точки зрения, принципиально механизм их функционирования описывается как движение «грузика на пружине» [4] (рис. 3).

Запишем уравнение движения чувствительной массы акселерометра в проекции на ось чувствительности:

a a = g cos( a + ф ) + f' , где f' - удельная сила упругости, которая измеряется прибором.

Учтем несовершенство прибора, добавив мультипликативную (1 + ц ) и аддитивную А а ошибки. Показания акселерометра имеют вид

f = (1 + ц) f' +Аа = (1 + ц) [аа + g cos(a + ф)] +Аа.

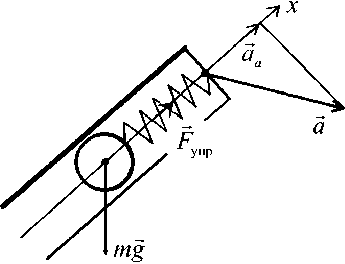
Рис. 3. Принципиальная схема функционирования акселерометра

Ошибка масштаба (1 + ц ) содержит также компоненты, связанные с тем, что ось датчика не лежит в плоскости движения вследствие неточности крепежа. Величины, вообще говоря, не постоянны, они меняются, например, в зависимости от температуры. Эти изменения происходят достаточно медленно, и на промежутках времени эксперимента в дальнейшем мы будем ими пренебрегать.

Учтем также эффект рассинхронизации по времени снятия показаний акселерометра и системы видеоанализа. Введем параметр запаздывания регистрации показаний акселерометра т s :

f ( t -т , ) = (1 + ц ) [ a_a ( t ) + g cos( a + ф ( t )) ] +A a .

В итоге выражение, связывающее показания акселерометра и системы видеоанализа, имеет вид f (t - т s) = (1 + ц) l sin(a - в)ф2 (t) + (1 + ц) l cos(a - в)ф( t) +

+ (1 + ц ) sin a [ - x 1 ( t ) cos ф - ( y 1 ( t ) + g ) sin ф ] +                             (2)

+ (1 + ц ) cos a [ - x 1 ( t ) sin ф - ( y 1 ( t ) + g ) cos ф ] +A a .

Задача идентификации

Соотношение (2) содержит постоянные величины A а, ц , l, a , в , т _s , значения которых неизвестны, и их определение с использованием стандартных способов антропометрических измерений затруднено. В связи с этим, как и ранее в работе [6], необходимо использовать методы идентификации неизвестных параметров.

Будем считать тs малым по сравнению с характерным временем совершаемого движения и представим f (t - тs) в левой части (2) в виде двух первых членов разложения в ряд Тейлора f (t - тs)« f (t) - тsf (t). Получим f (t) = X1ф2 (t) + X 2ф( t) + X3 [-x1 (t) cos ф - (y (t) + g) sin ф] + + X4 [-^ (t) sin ф - (y (t) + g) cos ф] + X5 + X6f (t).

В уравнении (3) введены обозначения для комбинаций неизвестных параметров

A а, ц , l, a , в , т _s :

• X 1 = (1 + ц ) l sin( a - в ),

X ₂ = (1 + ц ) l cos( a - в ),

X ₃ = (1 + ц )sin a ,

X 4 = (1 + ц ) cos a ,

X ₅ =A a ,

^X 6 = ^т s .

Соотношение (3) можно представить уравнением относительно неизвестных компонент вектора X = ( X 1 , X 2 , X 3 , X 4 , X 5 , X 5 ) T . Производные от измеренных величин в этом случае вычисляются по конечноразностным соотношениям. Соотношения вида (3), записанные для всех моментов времени t j ( j = 1, ^ , N 0 ), при которых измеряемые величины не содержат сбоев, образуют переопределенную систему уравнений

AX = B ,                                  (4)

где B = ( f ( t 1 ),..., f ( t_N )) T , а компоненты A j матрицы A задаются соотношениями

A 1 j =Ф 2 ( t j ),

A 2 j = ^{ф (} t j ),

A 3 j = - x ⁽ t j )^COs ф ⁽ t j ) - ⁽ y ⁽ t j ) + g ^)sin ф ⁽ t j ),

A 4 j = - x 1 ⁽ t j ) sin ф ⁽ t j ) - ^{( y} 1 ⁽ t j ) + g )COs ф ⁽ t j ),

A 5j = 1,

A 6 j = f ( t j ).

Здесь ф ( t j ), f ( t j ) - измерения, приписанные программным обеспечением системы съема информации к моменту времени t_j .

Задача получения из (4) значения X решается модифицированным методом наименьших квадратов [8, 14] и подробно рассмотрена для аналогичной задачи в [6].

Задача восстановления утерянных значений углов

Для решения задачи восстановления утерянных значений угла ф также используем уравнение (3), которое в данном случае применяем для участков с неполной информацией, где неизвестны координаты маркера в точке O 2 , а следовательно, и угол ф . Значения комбинаций параметров X_t получены на предшествующем этапе идентификации.

Рассмотрим два варианта процедуры восстановления утерянной информации системы видеоанализа. Первый из них использует традиционный подход нерекуррентного метода наименьших квадратов, аналогично работам [6, 7]; второй – процедуру калмановского сглаживания [14].

Использование неитерационного метода наименьших квадратов

Сведение задачи восстановления утерянных значений углов к решению системы линейных уравнений вида Ax = B ранее было подробно описано в работах [6, 7]. Повторим здесь вкратце основные этапы этой процедуры.

Будем считать, что утеряна информация, полученная системой в моменты времени t i ( i = 1,..., N ) . Обозначим ф = го , ф = s и представим в каждый момент времени ф , го , s в виде суммы априорной оценки, обозначенной индексом a , и малой поправки: ф = ф _a + ф_д , го = ф a + го_д , s = ф a + 8_д . Проведем линеаризацию уравнения (3) по ф_д , го_д , 8_д . Получим

С 1 ⁽ t ) ф д ⁺ С 2 ⁽ t ^{) го} д ⁺ С з ( t ) 8 д = b ⁽ t ),                                   ⁽⁵⁾

где обозначения

С (t) = X3 (X (t) sin фa — (у1 (t) + g) COS фa ) — X4 (x1(t) COS фa + (y1 (t) + g)Sin фa X c 2( t) = 2го aX1,

С 3 ( t ) = X 2 ,

b ⁽ t ) = f ⁽ t ) — ^ГО a ^X 1 — ^s a ^X 2 ⁺ X 3 ^{( X} 1 ⁽ t ) ^Cos ф a ^{+ ( y} 1 ⁽ t ) ⁺ g ) ^sin ф a ) ⁺

^{+ X} 4 ^{( X} 1 ⁽ t ) ^Sin ф a — ⁽ У ⁽ t ) ⁺ g ) ^COS ф a ) — ^X 5

являются известными функциями измеряемых величин x ₁( t ), y ₁( t ) , идентифицированных параметров X_i и задаваемой пользователем априорной оценки Ф a ( t ). Уравнение (5) записывается для моментов времени t i ( г = 1,..., N ), в которые производится извлечение информации . Для вычисления производных от значений ошибок будем использовать разностные приближения

^Ю д ⁽ t i ) = ⁽ Ф д ⁽ t i + 1 ) -Ф д ⁽ t i ))/ ^т , Е д ⁽ ti ) = ⁽ Ф д ⁽ t i + 1 ) - ² Ф д ⁽ t i -) + Ф д ⁽ t -1 )) / ^т 2 .

Подставляя разностные соотношения в уравнение (5), составим систему уравнений q^(tiJ+q2,Фд(ti)+qл(tiJ=b(ti), i = 1,-,N,                  (6)

где qu = c3( ti)/ T2, q 2 i = c1( t) - c 2( ti)/T-2 cз( ti)/T2, q з i = c 2( ti)/T+cз( ti)/ T2.

Здесь величины ф_д ( 1 0 ), ф_д ( t_{N + 1}) можно получить, используя полученные из показаний системы видеоанализа значения угла в моменты времени до и после интервала восстановления.

Проведем все описанные выше рассуждения для второй оси чувствительности акселерометра. Получим уравнения, аналогичные (6):

^ 1 , -Ф д ⁽ t -1 ) ^{+ г} 2 , Ф д ⁽ t i ) ^{+ г} з , Ф д ⁽ t +1 ) = d ⁽ t i ), i = 1, - , N .                         ⁽⁷⁾

Таким образом, создана система из 2 n линейных уравнений вида (6), (7) с N неизвестными ф_д ( t 1 ),..., ф_д ( t_N ). В матричном виде она имеет вид

A e x = B e ,

где

	^ q 21	q 31	0	0	0	...	0 1
	q 12	q 22	q 32	0	0	...	0
	0	q 13	q 23	q 33	0	...	0
	0	...	0	... 0	q 1 N - 1	q 2 N - 1	q 3 N - 1
AP =	0	...	0	0	0	q 1 N	q 2 N
e	r 21	r 31	0	0	0	...	0
	r 12	r 22	r 32	0	0	...	0
		r 13	r 23	r 33	0	...	0
	0	...	0	... 0	r1 N - 1	r2 N - 1	r3 N - 1
	1 0	...	0	0	0	r 1 N	r2 N >

( Фд(ti) )x =

(ф д ( t N ) )

^ ^{Ь (} t i ) - ^ цфд ⁽ t 0 ) ^b ( 1 2 )

...

^Ь ( t N - 1 )

B _ b ⁽ t N ) - q 3 N ^ф д ⁽ t N + 1 ) e        d ⁽ t i ) ^- Г цфд ⁽ t 0 )

d d ( tN-,)

( d ⁽ t N ) ^r 3 n ^ф д ⁽ t N + 1 ) >

Систему (8) решим методом наименьших квадратов [8, 14]:

~~ _ ( A , A , ) ^{- 1} A , B ,

Тем самым вычислим оценку ф в моменты времени t i ( i _ 1,..., N ):

^ф ( t i ) = Ф a ( t i ) ^{+ ф} Д ( t i ).

Для повышения точности применяется итерационная процедура. На первом шаге в качестве априорной оценки на интервале восстановления [ t_i , t_N ] используются значения линейной функции времени:

Ф a ⁽ t ) = ⁽ Ф ⁽ t N + 1 ) — Ф ⁽ t 0 ⁾⁾⁽ t — t 0 ) / ⁽ t N + 1 — t 0 ) ⁺ Ф ⁽ t 0 ^).

На каждом следующем интервале в качестве «априорных» значений принимаются значения, полученные на предыдущем шаге.

Отметим, что изложенный алгоритм может быть применен в случае, когда рассматривается только одна из осей чувствительности акселерометра. Для этого в матрицах A и B нужно оставить только первые либо последние N строки.

Использование калмановского сглаживания

Другой алгоритм восстановления угла ф по показаниям акселерометра основывается на процедуре сглаживания с помощью фильтрации Р. Калмана [14]. Для использования этой процедуры необходимо свести задачу восстановления к задаче оценивания вида xn+1  Ф nxn + B ^ n, zn _ Hnxn + rn.

Здесь x n - дискретный вектор состояния; ^ _n и r n - возмущение и погрешность измерений, моделируемые дискретным белым шумом; z n - измерения; Ф _n и H_n -известные матрицы. В этом случае решение задачи возможно с помощью сглаживающего алгоритма, основанного на методе фильтра Калмана [1, 14].

Сделаем предположение о гладкости решения, аналогичное тем, которые принимаются при сглаживании сигналов для поиска случайного поля [9, 12], 2

8 n + i =8 n + L n , где L n - дискретный белый шум. Интенсивность шума о _ является параметром задачи. Используя конечноразностные соотношения, получим уравнения, связывающие значения углов, угловых скоростей и ускорений в n -й и ( n + 1)-й моменты времени:

ф(tn+1) = Ф(tn) + ю(tn)т + 8(tn )т2 / 2, ю( tn+1) = ю( tn ) + 8( tn )т, 8(tn+1) = 8(tn )   Ln , где т - шаг дискретизации системы.

Введем обозначение x ( t ) = ( ф ( t ), ю ( t ), 8 ( t )) T . Здесь x n - значение вектора x в моменты времени t_n ; x_n = ( ф ( t_n ), ю ( t_n ), 8 ( t_n )) T . Тогда x_{n + 1} = Ф _nx_n + BL n _n , где

Ф

n

' ^{1 т т} 2 /²'

0 1

0 01

V7

B = 0

1V17

Для получения формализованного измерения z_n = H_nx_n + r_n представим правую часть уравнения (3), записанного для первой оси чувствительности акселерометра, в виде функции / 1 = / 1 ( x ). В качестве приближенного значения функции f в точке x = x_n используем разложение в априорной точке x = x a :

/ 1 ( x n ) * / 1 ( x a ) + H n 1 ( x n - x a ),

T

где H_{n 1} =

f 5 x

x = x a

= \ a n1 , a n1 , a n1 , a n1

).

a n 1 = ^X 3 [ ^x 1 ( t n ) ^sin( ф ( t n )) ^{- (} y 1 ( t n ) ⁺ g ) ^С08( ф ( t n ))) ] ^-

- X4 [x1 (tn ) COS(Ф(tn )) — (y1 (tn ) + g) 81П(Ф(tn )))] , an1 = 2 X1®( tn), an1 = X2,

4 a n 1 = 1.

«Измерениями» следует считать z_n 1 = H_n 1 x a - / 1 ( x a ) = H_n 1 x_n + r_n 1 и аналогично для второй оси чувствительности акселерометра z_n 2 = H_n 2 x a - / 2 ( x a ) = H_n 2 x_n + r_n 2 . Ковариации случайных процессов r_{n 1} , r_{n 2} типа белого шума, моделирующих случайную ошибку измерений акселерометра, задаются величиной о _r . Априорная точка x_n^a является результатом этапа прогноза в методе фильтра Калмана [1, 14].

Суммируя все вышесказанное, получаем следующую формальную задачу: xn+1 = Ф nxn + B^n , M[^n^m ] = °25nm , zn = Hnxn + rn , M[rnrmT ] =

Ф

n

к

T

т ² / 2 )

T

,

Hn =

к a n 2

a

a

n ²1 n ²2

a

a

n ³1 n ³2

r к 0

B = 0 ,

к17

a

a

4 ⁴ ) T n 1

' n 2 7

,

а02 1

° r 7

^ nm ,

zn = ⁽ z n 1 z n 2 ) ,

r n = ⁽ r n 1 r n 2 ) T .

Для построения оценки с минимальной дисперсией ошибки применяется алгоритм фильтра Калмана в прямом и обратном времени. Начальные и конечные значения вектора состояния x и ковариационной матрицы P задаются исходя из значений ф до и после интервала восстановления, полученных по показаниям измерительных систем

x 0	= ( Ф о , Ю 0 , £ о ) T ,
xN	= ( ф N , ® N , ^ N ),
	4 Р 1    0    0
P 0	= P n =   0   p 2   0
	к 0   0 p 3

.

Для получения оценки ^~ x_N и,

соответственно,

ф N применяется алгоритм

оптимального сглаживания на фиксированном интервале в соответствии с [1, 14].

Проверка эффективности решения задачи восстановления

Разработанные алгоритмы опробованы на результатах обследования, проведенного в Государственном научном центре «Институте медико-биологических проблем Российской академии наук». На латеральные проекции центров вращения в суставах правой нижней конечности обследуемого были наклеены светоотражающие элементы (катафоты). Испытуемый совершал движения (типа приседания), записываемые видеокамерой системы видеоанализа «Видеоанализ–2 D » с одновременной регистрацией показаний двухкомпонентного акселерометра из комплекта измерительной биомеханической аппаратуры MuscleLab 4000 e фирмы Ergotest (Норвегия), размещенного на голени, как показано на рис. 1.

Частота кадров видеозаписи – 50 Гц. Частота снятия показаний акселерометра – 100 Гц. Для удобства дальнейших вычислений частота записи акселерометра снижается путем выбора только четных измерений.

Проведено три записи по шесть-семь приседаний для одного обследуемого. По результатам измерений вычислялись значения координат маркеров. Показания системы видеоанализа и акселерометра для одной из записей представлены на рис. 4.

Анализ структуры сигнала акселерометра позволил выявить значительную колебательную составляющую частоты ~10 Гц, вероятнее всего являющуюся следствием мышечного тремора. Для того чтобы минимизировать погрешность, вызванную влиянием тремора и ошибкой дискретизации данных, было произведено предварительное сглаживание сигнала акселерометра окном Ханна шириной 1 с [11]. Ширина окна обусловлена характерными частотами движения обследуемого 0,2–0,5 Гц.

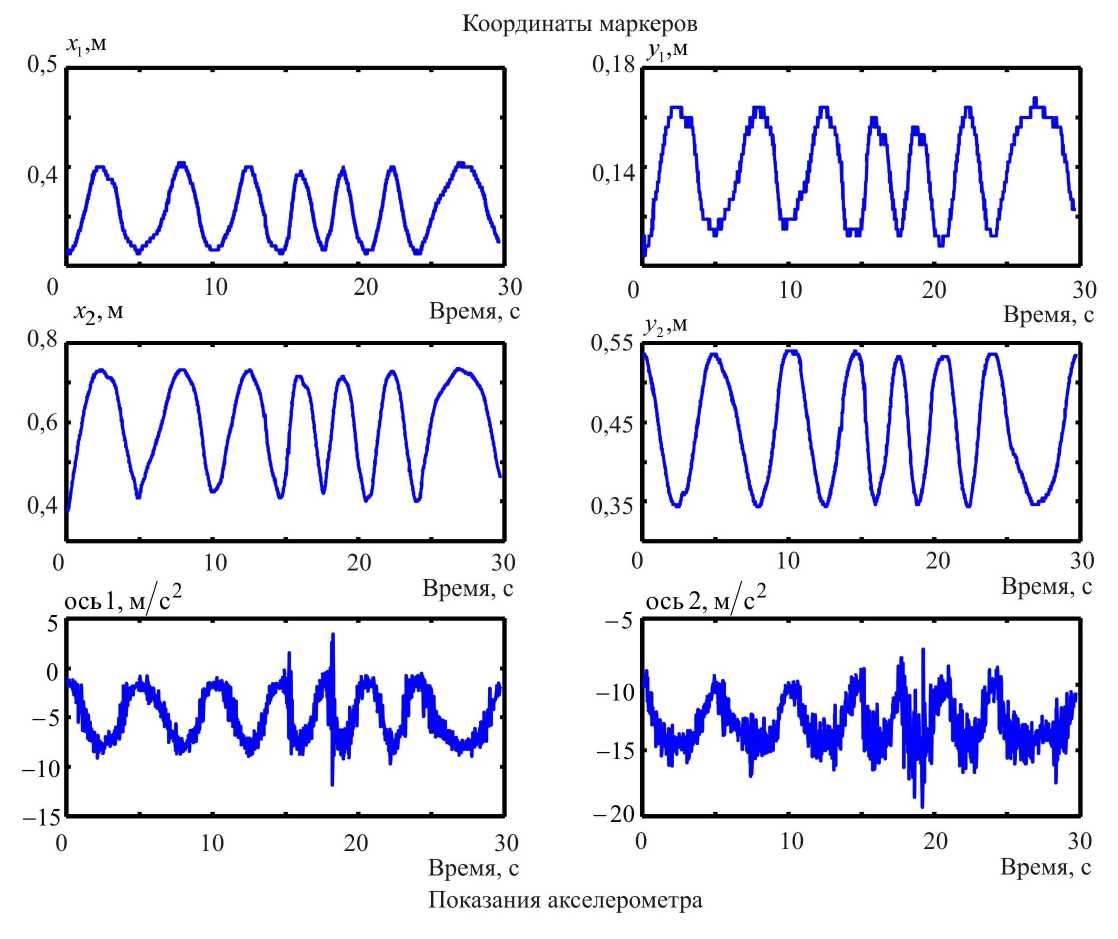
Рис. 4. Пример показаний системы видеоанализа и акселерометра

Для каждой из осей чувствительности акселерометра

производилась идентификация неизвестных параметров в соответствии с изложенным ранее алгоритмом.

Анализ зависимости результатов идентификации от длительности участка идентификации показал, что участок длительностью 5 с, сравнимый с временем полного приседания, позволяет достаточно хорошо идентифицировать неизвестные компоненты вектора X в том смысле, что увеличение длины этого участка до большей продолжительности приводит к изменению оценок компонент X на 5%. При увеличении длины интервала свыше 15 с число обусловленности для решаемой задачи не изменяется.

Полученные идентифицированные параметры далее использовались в задаче восстановления. На рис. 5 представлены графики результатов постановления и ошибок для характерного интервала. Параметры фильтра Калмана в результате подбора принимались равными о ^ = 100 рад/с², о r = 10м/с².

В процедуре восстановления с использованием метода наименьших квадратов производилось две итерации. Начиная со второй итерации, порядок величины среднеквадратичного отклонения остается неизменным и равен 10–6 рад, поэтому достаточно выполнить всего две итерации.

График зависимости среднеквадратичной ошибки восстановления от длины интервала восстановления при фиксированном левом конце представлен на рис. 6.

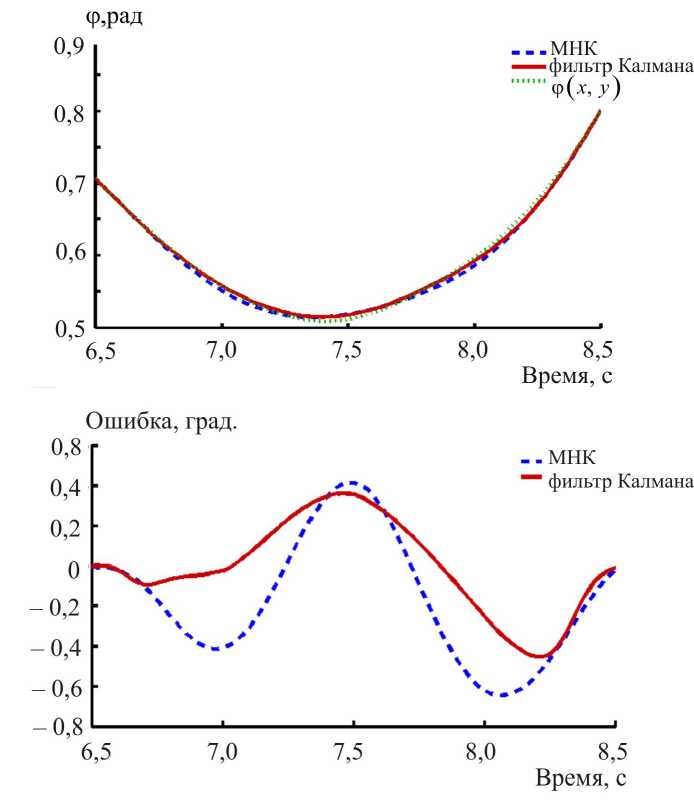
Рис. 5. Результаты восстановления на интервале (6,5–8,5) и соответствующая ошибка для алгоритмов с использованием метода наименьших квадратов (МНК) и фильтра Калмана

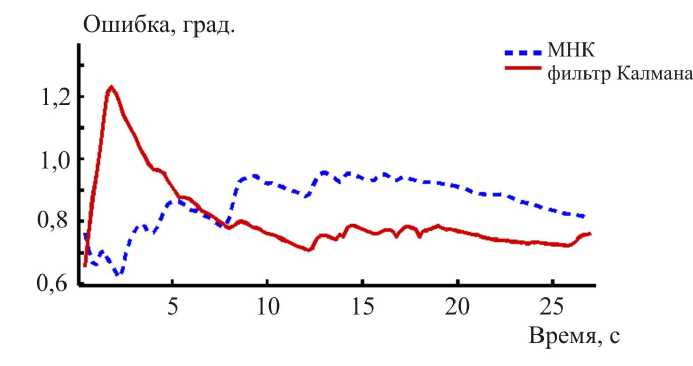
Рис. 6. Зависимости среднеквадратичной ошибки восстановления от длины интервала.

Обозначения – см. рис. 5

Как видно, порядок погрешности восстановления сохраняется при увеличении интервала до нескольких секунд.

В среднем среднеквадратичное значение ошибки восстановления для интервала в 1 с для метода наименьших квадратов составило 1,06·10–3 рад, а для процедуры сглаживания – 1,27·10–3 рад. Изменения среднеквадратичного значения ошибки от записи к записи не наблюдалось.

Результат калмановского сглаживания не всегда оказывается точнее алгоритма с использованием метода наименьших квадратов. Тем не менее порядок ошибки для обоих методов совпадает, и точность восстановления оказалась приемлемой, так как для системы видеоанализа приборная погрешность определения угла ~1°.

Заключение

Рассмотрена задача восстановления показаний системы видеоанализа, когда в качестве дополнительной информации используются измерения двухкомпонентного датчика линейных ускорений. Обсуждаются два алгоритма восстановления: первый основан на методе наименьших квадратов, второй – на калмановском сглаживании. Обязательной процедурой является идентификация параметров модели.

В случае применения метода наименьших квадратов использование нескольких итераций позволяет существенно повысить точность восстановления. При этом на экспериментальных данных ошибка восстановления в среднем оказалась в пределах точности измерений системы видеоанализа.

Дискретный фильтр Калмана учитывает условия гладкости, вычислительно упрощает процедуру восстановления и позволит в дальнейшем эффективно использовать метод стохастических мер оцениваемости [1] при решении более сложных практических задач. Однако при этом нетривиальным является подбор ковариаций шумов, участвующих в модели движения, и измерений, что затрудняет решение задачи. Следует отметить, что эти ковариации остаются неизменными для всех тестов, проводимых одновременно, их подбор можно осуществить на тестовом движении, проводимом в начале серии обследований.

Благодарности

Работа выполнена при частичной поддержке РФФИ (грант 09–01–00809).

100                     ISSN 1812-5123. Российский журнал биомеханики. 2012. Т. 16, № 1 (55): 89–101