О двух способах расчётного определения объёмной массы сильвинитовых руд по их химическому составу на примере Талицкого участка Верхнекамского месторождения

При подсчёте запасов калийных и ка-лийно-магниевых солей на Верхнекамском месторождении (ВКМС) с 1958 г. применяется расчётный способ определения объёмной массы полезных ископаемых по данным об их химическом составе, что соответствует методическим рекомендациям ГКЗ, в том числе и действующим [4]. При этом в отношении солей разного состава применяются разные методики расчётов. В частности, для определения объёмной массы сильвинитов используются данные о содержании только главного компонента KCl и регрессионный способ расчётов по уравнениям простой среднеквадратической регрессии вида dлаб. = a - b • Ckci , (1)

которые отражают зависимость лабораторных определений объёмной массы образцов сильвинитов d лаб. от содержаний в них хлористого калия ( C KCl ) .

Для вычисления объёмной массы карналлитовых пород и смешанных солей используются данные о содержаниии трёх компонентов KCl, NaCl и MgCl 2 и метод пересчёта химического состава солей на минеральный с последующим определением массы входящих в состав руды минералов пропорционально их содержанию и минералогической плотности. На действующих рудниках ВКМС объёмные массы калийно-магниевых руд рассчитываются теми же способами.

В 2005 г. при рассмотрении ТЭО разведочных кондиций по Соликамскому и Ново-Соликамскому участкам детальной разведки ВКМС экспертная комиссия ГКЗ Роснедра рекомендовала разработать единую для всех типов солей методику расчётного определения объёмной массы по данным об их химическом составе. Эта рекомендация была выполнена в 2006 г. в рамках переоценки запасов по Соликамскому, Ново-Соликамскому и Быгельско-Троицкому участкам, после апробации в ГКЗ была рекомендована к применению на других участках ВКМС. В представленной статье проанализированы результаты применения данной методики для расчётного определения объёмной массы сильвинитовых руд Талицкого участка ВКМС.

Методика 2006 г. является развитием ранее применявшегося метода пересчёта химического состава солей на минеральный и отличается увеличением количества компонентов, учитываемых при определении объёмной массы, с трёх до пяти (KCl, NaCl, MgCl 2 , CaSO 4 и нерастворимый в воде остаток Н.О.).

Метод базируется на следующей формуле теоретической объёмной массы руд, в которой используется соотношение сумм масс и объёмов минералов, входящих в природную многокомпонентную минеральную систему:

л = X mi = Е (m о • Ci) = Ес.

теор.   X V у ( m о • C i )   V C ’

Е d   Е d где dтеор. – теоретическая минералогическая объёмная масса пробы; mi, Vi, Сi, di – соответственно масса, объём, содержание и минералогическая плотность i-го минерала; m0 – масса пробы.

К числу основных минералов, от которых зависит объёмная масса солей ВКМС, авторы методики относят сильвин, карналлит, галит, ангидрит и комплекс минералов нерастворимого в воде остатка Н.О. На Талицком участке в состав последнего входят кварц, полевые шпаты, глинистые минералы, сульфаты и карбонаты.

Пересчёт химического состава солей на минеральный для сильвина и карналлита производится с использованием стехиометрических соотношений по MgCl 2 [5]

С и = C kci - С мда₂ • 0.7830,

С карн = C MgCl 2 • 2.9182,

а для галита, ангидрита и комплекса минералов Н.О. – по формулам:

Нгал   NaC[aQi,

Нанг .    CaSO0₄ ,

^v комп . Н . О .     Но . О. ,

где С сил ,

С карн , С гал ,

С анг и С комп.Н.О. – рас-

чётные содержания сильвина, карналлита, галита, ангидрита и комплекса минералов Н.О., % масс.; СKCl , СMgCl , СNaCl , СCaSO , CН.О. – содержания соответствующих компонентов солей, % масс.

Для вычислений по формуле (2) методикой рекомендованы следующие значения плотности (г/см3): сильвина – 1.989, карналлита – 1.60, галита – 2.16, ангидрита – 3.00, комплекса минералов нерастворимого в воде остатка – 2.70.

С учетом указанных значений плотности минералов и соотношений (3-4) формула (2) для определения теоретической минералогической объёмной массы солей ВКМС приводится к виду:

С + С  +
и теор .                 /'т C сил     Скарн	(5)
1.989   1.60

+ Сгал	+ С + С анг      комп . Н . О .
।   Сгал 2.16	СС ।      анг ।      комп . Н . О . 3.00    2.70
или
J      ( ска - d   =	C Mgci , • 0.7830 ) +	(6)
теор . С КС1	C MgCl 2 • 0.7830 +
	1.989

+ ( С м.С1, -2-9182 ) + C nC + C _CaSO, + С нО.

+ ^C MgSl_г ' 2-9182 + ^C Na_Cl + ^C CaSO 4 + ^С _Н . ₀ .

1.60        2.16    3.00    2.70

Для сильвинитовых руд Талицкого участка формула (6) после соответствующих преобразований и без учёта карнал литовой составляющей приобретает вид:

C kci - 0-783 • C_Mga2 +

d теор .

0.5028 • С_кс, - 0.3937 • С_м„_п +

KCl               MgCl ₂

⁺ NaCa + ⁺ CaSoSO + ⁺ НО . О .

+ 0.463 • С„_ап + 0.333 • С,^ _о + 0.370 • С_{н о}

NaCl             CaSO              Н . О

Следует отметить, однако, что величины теоретической объёмной массы, рассчитанные по формулам (5-7), будут всегда завышены по сравнению с действительной объёмной массой природных типов солей, определенной в лаборатории методом взвешивания ненарушенных образцов солей в жидкости. Причиной этого является то, что в знаменателях формул (2) и (5-6) используется не объёмная масса, а плотность минералов, которая не учитывает влияния пористости, трещиноватости, естественной влажности образцов соли и наличия газовожидких включений. Приводимые в формулах величины минералогической плотности характеризуют исследуемое вещество в плотном состоянии, т.е. только его твёрдую фазу без учёта пор, каверн, трещин и влажности, так как определяются пикнометрическим методом [5] по навеске предварительно измельчённого до крупности менее 0,1 мм и при этом сухого вещества. При определении же объёмной массы испытуемый образец имеет ту же самую структуру, текстуру, пористость, кавернозность, трещиноватость и влажность, что и в естественных природных условиях (в массиве полезного ископаемого). Поэтому объёмная масса учитывает не только твёрдую фазу вещества, но и наличие жидкой и газообразной составляющих. Для лабораторного определения объёмной массы солей, растворимых в воде, используется метод взвешивания исследуемого образца в керосине (толуоле) или взвешивания предварительно покрытого парафином образца в воде [5].

Для устранения такого систематического завышения рассчитанной объёмной массы по сравнению с лабораторными определениями методикой 2006 г. в формулу (2) введён понижающий коэффициент К < 1, который отражает суммарное влияние всех неучтённых факторов: пористости, трещиноватости, естественной влажности, присутствия в солях газовожидких включений, а также некоторого количества второстепенных и акцессорных минералов. Поэтому для природных типов сырых солей ВКМС формулы (2) и (5-7) приведены к виду:

, расч. прир.      теор.      ,

где d расч.прир. расчётная объёмная масса природного типа солей; К - коэффициент, отражающий влияние неучтенных фаз ( К < 1). При этом коэффициент К рассчитывается через отношение средних значений экспериментальных и вычисленных по формулам (6) и (7) величин объёмной массы солей на основе имеющихся по участку месторождения лабораторных определений, причём величина коэффициента К принимается постоянной по исследуемому участку ( K=const ).

Проанализируем результативность методики 2006 г. на примере сильвинитовых руд Талицкого участка. При детальной разведке участка в 1968–1969 гг. было выполнено 47 лабораторных определений объёмной массы образцов сильвинитов, отобранных из пластов КрIII (2 шт.), КрII (24 шт.), Кр1 (3 шт.), А (14 шт.) и Б (4

шт.). Исследования проводились методом гидростатического взвешивания проб в очищенном керосине. Однако при сопоставлении экспериментальных и расчётных по формуле (8) величин объёмной массы из этой выборки пришлось исключить данные по 5 аномальным пробам, так как на графике сопоставления двух указанных параметров (рис. 1, Б) точки, соответствующие упомянутым 5 пробам, оказались за пределами области допустимых отклонений для уровня значимости 0.05.

Проведенный корреляционный анализ (таблица) показал наличие тесных и статистически значимых, а в некоторых случаях – очень тесных корреляционных связей изученных шести параметров друг с другом, кроме содержания MgCl2, которое не коррелируется ни с объёмной массой сильвинитов, ни с содержаниями других компонентов. Корреляционные графики экспериментальных и рассчитанных по формулам (7, 8) величин объёмной массы по 42 образцам сильвинитов отражены на рис. 1, где показаны также теоретические и эмпирические линии регрессии и границы области допустимых отклонений. Последняя ограничена линиями, проведёнными по отношению к теоретической линии Y=X на расстояниях, равных удвоенным относительным среднеквадратическим отклонениям расчётных величин объёмной массы от лабораторных определений, что отвечает уровню значимости 0.05.

Матрица коэффициентов корреляции объёмной массы и содержаний основных компонентов сильвинитовых руд Талицкого участка по изученной выборке

Параметр		Объёмная масса образцов	Содержания компонентов
			KCl	MgCl 2	NaCl	CaSO 4	Н.О.
		Y	Х 1	Х 2	Х 3	Х 4	Х 5
Объёмная масса образцов	Y	1.000	-0.913	-0.046	0.903	0.587	0.437
Содержание KCl	Х 1	-0.913	1.000	-0.036	-0.990	-0.635	-0.455
Содержание MgCl 2	Х 2	-0.046	-0.036	1.000	0.009	-0.103	0.166
Содержание NaCl	Х 3	0.903	-0.990	0.009	1.000	0.562	0.328
Содержание CaSO 4	Х 4	0.587	-0.635	-0.103	0.562	1.000	0.586
Содержание Н.О.	Х 5	0.437	-0.455	0.166	0.328	0.586	1.000

Примечание: объём выборки N = 42, r крит. α=0.05 = |0.303|. Жирным шрифтом выделены статистически незначимые оценки коэффициентов корреляции

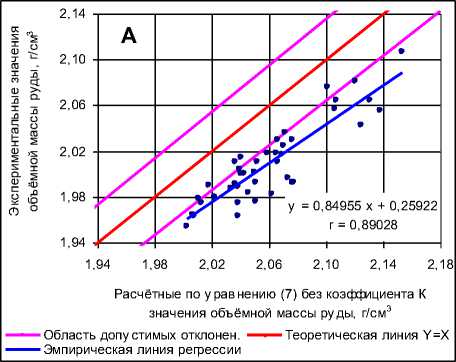
Рис. 1. Графики зависимости экспериментальных и расчётных величин объёмной массы сильвинитов Талицкого участка: А – без коэффициента К, Б – с коэффициентом К

Расчётные по уравнению (8) с коэффициентом К значения объёмной массы руды, г/см3

^^^мОбласть допустимых отклонен. ^^^^" Теоретическая линия Y=X ^^^^^Ш Эмпирическая линия регрессии

Как видно на рис. 1, А, большинство 42) оказались за пределами области допу-точек двумерного распределения (34 из стимых отклонений, в то время как при

полном соответствии коррелируемых параметров друг другу все точки должны группироваться в границах доверительного интервала вблизи теоретической линии Y=X, проведенной под углом 45° к осям координат. При этом эмпирическая линия регрессии, аппроксимирующая зависимость лабораторных определений объёмной массы от рассчитанных по формуле (7) теоретических значений, отражает, как и следовало ожидать, систематическое и при этом довольно существенное завышение расчётных величин относительно экспериментальных.

Для устранения этого несоответствия теоретические значения объёмной массы откорректированы, согласно методике 2006 г., по формуле (8) путем умножения на постоянный понижающий коэффициент K=const , который рассчитан через отношение средних по выборке Талицкого участка экспериментальных и вычисленных по формуле (7) значений объёмной массы сырых сильвинитовых руд: К = =2.009 : 2.060 = 0.975. Эта величина сопоставима с аналогичным коэффициентом по соседнему Быгельско-Троицкому участку, где К = 0.979. В качестве абсолютной погрешности принято среднеквадратическое отклонение рассчитанных по формуле (8) величин объёмной массы относительно лабораторных данных, что составило 0.017 г/см³, относительная погрешность 0.85 %. Указанные величины сопоставимы с аналогичными показателями по Быгельско-Троицкому участку -0.015 г/см³ и 1.3 %.

Как видно на рис. 1, Б, после корректировки расчётных величин объёмной массы с помощью постоянного понижающего коэффициента К данные всех включенных в выборку 42 анализов не выходят за пределы области допустимых отклонений, а эмпирическая линия регрессии очень близка к теоретической линии Y=X. Профессором В.Ф. Мягковым в работах [6, 7] показано, что соотношение, подобное случаю, отражаемому графиком рис. 1, Б, свидетельствует о приемлемом уровне случайных погрешностей определения анализируемого параметра, не превышающем допустимых величин, а также об отсутствии статистически значимых систематических погрешностей.

В отношении анализируемой выборки вывод о допустимом уровне случайных погрешностей подтверждается расчётами F -критерия Фишера, вычисленного по известной методике [1, 2, 3, 8], эмпирическое значение которого ( F эмп = 1.039) оказалось меньше критического ( F kpum.0,05 = 1.70) для уровня значимости 0.05 при количестве степеней свободы f i = f 2 = N - 1= = 41. Вывод об отсутствии статистически значимой систематической погрешности доказывается сравнением эмпирического значения критерия Стьюдента ( t _3Mn. = 0.30) с критическим значением ( t kpum.0,05 = 1.99) для уровня значимости 0.05 при количестве степеней свободы f = N 1 +N 2 - 2 = 82.

Следует отметить, однако, что, судя по графику рис. 1, Б, небольшая систематическая погрешность, хоть и статистически незначимая, в расчётах по формуле (8) всё-таки присутствует. Причём эта погрешность является знакопеременной [6, 7], так как меняет знак относительно точки пересечения теоретической и эмпирической линий регрессии с координатами d pK = d э = 2.015 г/см³, которая очень близка к центру двумерного распределения (двумерному среднему с координатами d рK = d э = 2.009 г/см³). На графике рис. 1, Б это выражается в том, что теоретическая и эмпирическая линии регрессии расходятся влево и вправо от точки их пересечения и чем дальше, тем больше. Причем влево от точки пересечения при d pK < 2.015 г/см³ эмпирическая линия регрессии отражает завышение экспериментальной объёмной массы по отношению к теоретической расчётной с коэффициентом К , а вправо (при значениях d pK > 2.015 г/см³), наоборот, занижение.

Следовательно, поправочный коэффициент К в формуле (8) не должен быть постоянным, как предусмотрено методикой 2006 г., а его величина должна зависеть от самих значений рассчитанной по формуле (7) объёмной массы сильвинитов. Что ка- сается способа определения коэффициента К, принятого обсуждаемой методикой, то он действителен лишь для условий, близких к центру двумерного распределения.

В работах В.Ф. Мягкова [6, 7] справедливо отмечено, что способ сравнения средних значений сопряженных измерений, как и критерий Стьюдента, позволяет оценить систематичность расхождений сравниваемых замеров только в среднем и поэтому отражает лишь статику изучаемого явления, но не учитывает его динамики, т.е. того, как изменяются систематические погрешности в зависимости от самих значений измеренного свойства. Этого недостатка лишён регрессионный метод обработки результатов измерений, который позволяет регулировать размер вводимых поправок с помощью уравнения регрессии в зависимости от величины самих замеров [6, 7]. При этом регрессионный способ помогает обнаружить систематические погрешности даже в тех случаях, когда при сравнении средних они просто не выявляются, как в рассматриваемом случае с объёмной массой сильвинитов, когда систематические погрешности меняют знак относительно точки пересечения теоретической и эмпирической линий регрессии, а положительные и отрицательные отклонения эмпирических значений от теоретических взаимно компенсируют друг друга.

Для устранения отражаемых графиком рис. 1, Б статистически незначимых систематических расхождений экспериментальных и рассчитанных по формуле (8) значений объёмной массы сильвинитов необходимо использовать уравнение регрессии, показанное на графике рис. 1, А. Другими словами, для Талицкого участка при расчётах объёмной массы сырых сильвинитовых руд dpac4.npup.ucnp. правильнее использовать не формулу (8), а уравнение dpac4пририспр = 0.84955 • dР + 0.25922 , (9) расч.прир.испр. теор.

где dmeop. - теоретическая минералогическая объёмная масса, рассчитанная по формуле (7) на основе данных о химическом составе руд.

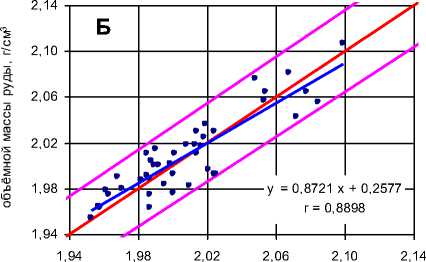
Как видно на рис. 2, отражающем ре- зультаты такой корректировки, введение поправок по уравнению (9) в расчёты объёмной массы сильвинитов позволило полностью устранить не только систематическое завышение расчётных по формуле (7) величин по отношению к экспериментальным данным (рис. 1, А), но и то небольшое статистически незначимое систематическое расхождение экспериментальных и расчётных по формуле (8) значений, которое отражает график на рис. 1, Б. При этом эмпирическая линия регрессии на рис. 2 полностью совпала с теоретической линией Y=X. Кроме того, с помощью уравнения (9) удалось немного уменьшить размер среднеквадратических отклонений откорректированных расчётных величин от лабораторных определений объёмной массы: абсолютных - с 0.017 до 0.016 г/см3, относительных - с 0.85 до 0.80 %. На рис. 2 это выражено как небольшое уменьшение ширины доверительного ин-

Рис. 2. График корреляции экспериментальных и расчётных по уравнению (9) значений объёмной массы сильвинитовых руд Талицкого участка

Отметим при этом, что расчёты по уравнению (9) равносильны использованию в уравнении (8) не постоянного понижающего коэффициента К=const, равного отношению средних по выборке экспериментальных и вычисленных по формуле (7) величин объёмной массы сильвинитов, а динамического коэффициента Кдин., равного отношению к = дин.

0.84955 • d_meoв + 0.25922 теор .

d теор.

= 0.84955 +

0.25922

d теор .

.

Как следует из формулы (10) и рис. 3, величина динамического понижающего коэффициента К дин. практически функционально зависит от рассчитанных по формуле (7) значений объёмной массы сильвинитов, что и обусловливает фактически полное устранение систематических расхождений рассматриваемых величин.

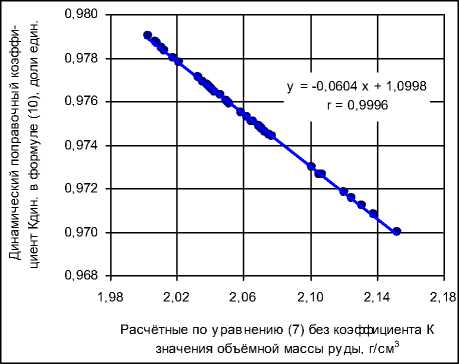
Рис. 3. Зависимость динамического поправочного коэффициент К дин. в формуле (10) от значений рассчитанной по формуле (7) объёмной массы руд

Как видим, предусмотренный методикой 2006 г. расчётный способ определения объёмной массы сильвинитовых руд характеризуется, во-первых, громоздкостью пересчётов по уравнению (7) компонентного состава руд на минеральный, во-вторых, необходимостью корректировки результатов с помощью постоянного для данного объекта поправочного коэффициента К. Однако этот коэффициент не устраняет полностью систематических расхождений экспериментальных и вычисленных по формуле (7) величин.

Указанных недостатков лишён регрессионный метод, который позволяет рассчитать объёмную массу с помощью уравнения множественной линейной регрессии напрямую через данные о химическом составе сильвинитовых руд без промежуточных пересчётов их компонентного состава на минеральный. При этом очень важно, что регрессионный метод не требует последующей корректировки результатов вычислений, так как при его использовании систематические расхождения между экспериментальными и расчётными величинами объёмной массы просто отсутствуют. Проанализируем результативность этого способа на примере Талицкого участка.

Множественная линейная регрессия вида m

Y = a о + £ a,-X i          (11)

i = 1

строится на основе учёта всех возможных взаимодействий между переменными и их сочетаниями [1-3, 8-11]. Оценка общего вклада независимых переменных Х i в изменчивость зависимой переменной Y производится с помощью коэффициента множественной корреляции r мн. , а оценка относительного влияния каждой независимой переменной Х i – с помощью коэффициентов регрессии а i . Такое уравнение наилучшим образом (в смысле метода наименьших квадратов) описывает тенденцию распределения исходных данных в m -мерном пространстве признаков и позволяет оценить совместное влияние на зависимую переменную всех анализируемых независимых параметров [2-3, 10-11].

Для расчётов коэффициента множественной корреляции и коэффициентов мно-жественной регрессии по выборке из тех же 42 лабораторных определений объёмной массы сырых сильвинитовых руд Талицкого участка использована матрица парных коэффициентов корреляции между изученными шестью параметрами, отражённая в представленной выше таблице. В качестве независимых переменных Х 1 , Х 2 , …, Х 5 приняты содержания основных компонентов KCl, MgCl 2 , NaCl, CaSO 4 и Н.О. по данным химических анализов изученных образцов сильвинитовых руд, а в качестве зависимой переменной Y – их объёмная масса.

Оценка коэффициента множественной корреляции рассчитана по формуле [1, 3]

Г —Г I мн .        y ( X 1 , x 2

х 5 )

-

| R |

A yy

где | R | – определитель матрицы [ R ] парных коэффициентов корреляции, представленной в таблице, А yy – алгебраическое дополнение зависимой переменной Y с самой собой.

Коэффициенты множественной регрессии а i и а 0 определены по формулам [1, 3]

а_  Ayx. ■(- 1)

a/ —, i          Ayy

a® — Y — a • X i — a ₂ ■ X 2 —

— a^ • X 3 — a д • X 4 — a $ ■ X 5

где A _yx , A _yx , ..., A _yx – алгебраические дополнения зависимой переменной Y с независимыми переменными Х 1 , Х 2 , …, Х 5 , S и S – стандартные отклонения соответствующих переменных, Y , X 1 , X 2 , ..., X 5 – выборочные оценки средних значений этих переменных.

Алгебраические дополнения A , A ,

A ,..., A рассчитаны, согласно методике [1, 3], как детерминанты вспомогательных матриц парных коэффициентов корреляции размерами на единицу меньше исходной, т.е. 5 x 5. Эти матрицы получены из исходной матрицы 6 x 6 в представленной выше таблице путём удаления той её строки и того столбца, которые соответствуют индексам алгебраического дополнения. Так, для расчётов A yy требуемая матрица составлена путём удаления первой строки и первого столбца матрицы [ R ],        а        для        расчётов

A _{yx 1} , A _{yx 2} , A _{yx 3} , A _{yx 4} , A _{yx 5} – пу-тём удаления первой строки и соответственно второго, третьего, четвертого, пятого и шестого столбцов.

Требуемые детерминанты вычислены с помощью библиотеки встроенных функций в программе MS Excel 2003. При этом

знаки алгебраических дополнений в формуле (13) определяются множителем (–1) ^k , где k – сумма номера строки и номера столбца исходной матрицы [ R ]. Поскольку алгебраические дополнения в формуле (13) относятся к одной и той же первой строке исходной матрицы и отличаются только номерами столбцов, то множитель (–1) ^k будет равен +1 для столбцов с нечётным номером и –1 для столбцов с чётным номером.

Рассчитанное по данным исходной матрицы [ R ] значение множественного коэффициента корреляции для выборки из 42 лабораторных определений объёмной массы составило r мн. = 0.922, что свидетельствует об очень тесной множественной корреляционной связи объёмной массы сырых сильвинитовых руд Талицкого участка с содержаниями выбранных пяти компонентов. Наличие статистически значимой множественной корреляционной связи подтверждается сравнением эмпирического значения F -критерия Фишера F эмп. = =52.6 с теоретическим для 5 %-ного уровня значимости а о,о5 при числе степеней свободы f 1 = N – m = 42 – 5 = 37 и f 2 = m –1 = =5 – 1 = 4, которое равно F теор.0,05 = 5.74. Так как F эмп. >>  F теор. , то нулевая гипотеза о равенстве коэффициента корреляции нулю отвергается и связь считается статистически значимой.

Рассчитанное уравнение множественной регрессии для определения объёмной массы сырых сильвинитовых руд Талицкого участка по данным химических анализов о содержаниях пяти основных компонентов имеет вид:

d расч.сыр = 0.02062 • C kci + (15)

+ 0.01255 • CMgc_h + 0.02252 • C^_a +

+ 0.02058 • C_CaS0 + 0.02363 • С_{н 0} — 0.12046, CaSO ₄ Н . О .

где d расч.сыр. – расчётная объёмная масса сырых сильвинитовых руд (г/см³), С KCl , С_MgCl , С NaCl , С_CaSO , C Н.О. – содержания основных компонентов сильвинитов по данным их химического состава (% масс.).

График корреляции лабораторных определений и рассчитанных по формуле

(15) величин объёмной массы сырых сильвинитовых руд Талицкого участка приведён на рис. 4, который свидетельствует об очень хорошей сходимости сопоставляемых параметров: коэффициент корреляции равен 0.9218 при критическом значении r крит.0,05 = 0.303 для уровня значимости 0,05. При этом соотношение дисперсии тренда [8] ( S ² =0.001051), описываемого уравнением (15), и остаточной дисперсии ( S ² =0.000185) в относительных величинах составляет 85 % и 15 %, т.е. предложенное уравнение (15) учитывает 85 % общей дисперсии ( S ² =0.001236) зависимой переменной Y . Поэтому оно вполне может использоваться для прогнозирования объёмной массы сырых сильвинитовых руд Талицкого участка по дан ным об их химическом составе.

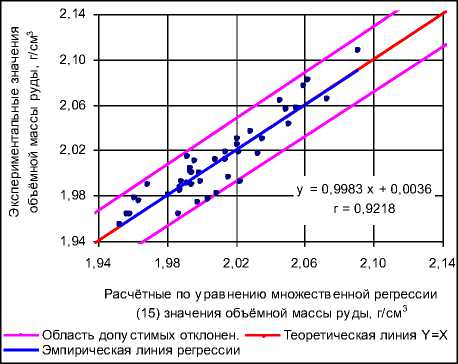
Рис. 4. График корреляции экспериментальных и расчётных по уравнению множественной регрессии (15) значений объёмной массы сырых сильвинитовых руд Талицкого участка

Проведённое сопоставление результатов расчётов объёмной массы сырых сильвинитовых руд Талицкого участка двумя способами (по откорректированной с помощью уравнения (9) методике 2006 г. и методом множественной регрессии по уравнению (15)) показало их очень хорошую сходимость (рис. 5): график корреляции демонстрирует очень тесную корреляционную связь между результатами расчётов (r = 0.962). При этом угловой ко- эффициент эмпирической линии регрессии приближается к единице, а сама линия регрессии – к теоретической линии Y=X.

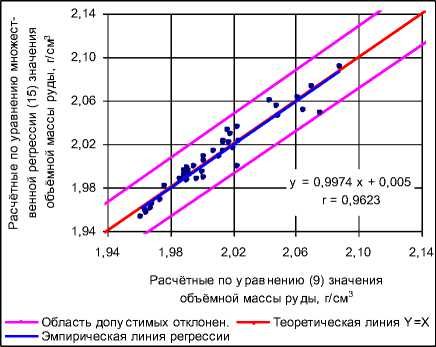
Рис. 5. График корреляции величин объёмной массы сырых сильвинитовых руд Талицкого участка, рассчитанных по уравнению (9) и уравнению множественной регрессии (15)

Таким образом, полученные результаты свидетельствуют о предпочтительности предложенного способа определения объёмной массы сильвинитовых руд по уравнению множественной регрессии (15), т.е. напрямую через данные о химическом составе сильвинитов без промежуточных пересчётов компонентного состава солей на минеральный.

Важно отметить, что метод множественной регрессии не требует последующей корректировки результатов вычислений ввиду отсутствия систематических расхождений между экспериментальными и расчётными величинами объёмной массы.

В заключение следует отметить, что вычисления объёмной массы сильвинитов по формуле (1) (т.е. как функции от содержаний только главного компонента KCl) с коэффициентами регрессии, принятыми при подсчёте запасов Талицкого участка в 1969 г. (a = 2.135 и b = 0.0018), также характеризуются систематическим завышением расчётных по формуле (1) величин объёмной массы по сравнению с лабораторными определениями. Это хорошо видно на рис. 6, А, где приведены данные по выборке из тех же 42 определений объёмной массы сильвинитов, как и на графиках рис. 1 и 2. Такое расхождение связано с недостаточной точностью вычисления коэффициентов регрессии a и b в 1969 г. Этот вывод подтверждается тем, что после выполненных нами уточнённых расчётов объёмной массы сильвинитов по той же формуле (1), но с откорректированными коэффициентами a = 2.1286 и b = 0.00188, систематическое расхождение экспериментальных и расчётных величин объёмной массы было устранено полностью, что отражает график на рис. 6, Б.

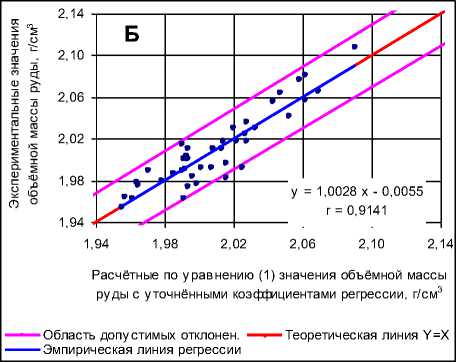
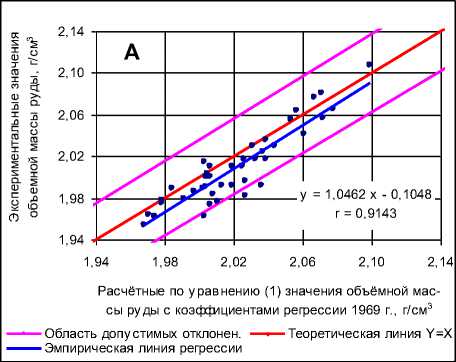
Рис. 6. Графики зависимости экспериментальных и расчётных по уравнению (1) значений объёмной массы сильвинитов Талицкого участка: А – с учётом коэффициентов регрессии 1969 г., Б – с учётом откорректированных коэффициентов регрессии

При этом среднеквадратические отклонения откорректированных расчётных величин от лабораторных определений объ-

ёмной массы уменьшились по отношению к данным 1969 г.: абсолютное – с 0.018 до 0.014 г/см3, относительное – с 0.90 до 0.70 %.

Анализ рис. 2 и рис. 6, Б свидетельствует о том, что результаты расчётов объёмной массы сильвинитов по методике 2006 г., учитывающей изменение содержаний пяти компонентов и откорректированной с помощью уравнения (9) (рис. 2), вполне сопоставимы с определениями объёмной массы по более простой зависимости (1) как функции от содержаний только главного компонента KCl (рис. 6, Б).

Однако для Талицкого участка более предпочтительным является либо метод множественной регрессии (рис. 4), либо откорректированная нами по уравнению (9) методика 2006 г. (рис. 2), так как основные пласты АБ, КрII и КрIII^а-б на этом участке характеризуются отчётливой тенденцией уменьшения содержаний KCl в краевой юго-восточной части залежи при существенном увеличении содержаний Н.О. и NaCl. Кроме того, при подсчёте эксплуатационных запасов всегда учитывается разубоживание полезного ископаемого, которое при разработке Талицкого участка будет происходить за счёт прирезки «коржей» в кровле пластов АБ и КрII, а также примешивания каменной соли в подошве этих пластов из-за локальных расхождений (в связи с мелкой складчатостью) траектории движения добычных комбайнов и гипсометрии пластов. Поэтому при определении объёмной массы сильвинитов Талицкого участка содержание вредных компонентов Н.О., NaCl и CaSO 4 должно обязательно учитываться. При этом будет обеспечено также единство методики расчётного определения объёмной массы для руд сильвинито-вого и карналлитового составов.