О дзета-подобных функциях и вещественном следе корней дзета-функции Римана

ср Д') = ДУ 2е^а^ ^2г*<р(1 — д).

< Подставим функцию у(д) указанного в теореме вида, в равенство (1) и заменим последовательно это равенство равносильными ему, используя известную формулу дополнения Г(д)Г(1 — д) = тг/ 8ттгд, а. также равенство Г(1 + д) = дГ(д):

<р(д)тгеог

(2тг)г sin ^Г(1 - дЩ^-^Щ! - д)

рДДе²”’² е °дГ

рДДе^Д-ДГ

По формуле удвоения Гаусса. ([1]; стр. 21) Г(^-)Г(1 — Д = 2^гЩгГ(1 — Д- Отсюда, продолжая цепь равенств, эквивалентных (1), имеем

<р(д)е°*2г    = (тг)г 2<Д1—д),

что, в свою очередь, равносильно соотношению (2). >

Полагая в теореме 1 <р(г) = 1, получаем

Следствие 1. Функция

Pz

2(г-1)Г(1 + |)

удовлетворяет уравнению Римана (1) тогда

и только тогда, когда, a = |1птг.

Далее, при a = ^1птг, из теоремы 1 выводим:

Следствие 2. Функция —---    ---—p(z), где ^ Е А(П), удовлетворяет уравне нию Римана (1) тогда, и только тогда, когда, 'ф(г) = р(1 — г) для любого z Е П.

Справедливо также

Следствие 3. Функция вида

eaz

2(г-1)Г(1 + |)

у (г), где a Е С, <р Е А(П) и ip(z) =

<р(1 — г) для любого z G П, удовлетворяет уравнению (1) тогда, и только тогда, когда, a = | In я.

Функцию вида h^ (г) : =

Pz

2(г — 1)Г(1 + —)

W(z) назовем дзета-подобной, если а Е С,

W Е А(С) и W — каноническое произведение, построенное по множеству нулей с такими свойствами:

• 1)    все нули W лежат в П;

• 2)    пусть zq — произвольный нуль W кратности ng; тогда zq и 1 — zq (а, следовательно, и 1 — zg) — нули W той же кратности;

• 3)    если {д. }/,.сф — все нули W (Ф — конечное или счетное множество) и п_к — кратность

  нуля z_k, k ^ 1, то ^Д_еф

  
  

  -77— < сю для любого Е > 0.

Положим

£

Ф :

Фз =

£

Ф1

Rez_k = I}; Ф₂ = ^ £ Ф : Kez_k = а, ^ ^; : z_k = I + %Х_к, 0 < Х_к < +ocl:

Ф4 = ^

s^=5

£

ф2

: z_k = a_k + iX_k, 0 <  a_k< |,

1 1А

—н — рч;

АеФз

Zk

Zk

АеФх

АеФз

1         1

--Н — + ----

Zk z_k 1 - z_k

1 \

+ с----— п/,.;

1 - z_k 7

~ \ 1 п_к

АеФ4 L

1 п_к

О дзета-подобных функциях и вещественном следе корней дзета-функции Римана 65

Имеем W(z) = УДДУДДД⁵™ ⁺⁵™ У д_ЛЯ любого zEC. Далее, для тех же г

АеФ3 L

АеФ3

АеФ3

АеФз

1 -

1 - г

7 + 1Х_к

iXk — | + 2

7 + iXk

^^^^^^^™

Тк

гХк + ^- z

^^^^^^^™

1 -

Пк

^^^^^^^™

1 - г

^^^^^^^™

iXk

iXk 2 + ^

^^^^^^^™

гХк

)

7 + гХ_к - z

Тк

Пк

гХк

^^^^^^^™

гХк

Тк

1 -

7 + iXk

Пк

7 + iXk

Аналогично показывается, что Угк) = РД1 — г) для всех г Е С. Таким образом, если h"^ — дзета-подобная функция, то W (г) = V(z)e^bz, где V(z) £ А(С), Уф) = К(1 — г) для любого zE Си 6 = Д' + S^ • Согласно следствию 3 имеем:

Следствие 4. Если № (г)

W(z) — дзета-подобная функция, то она удовлетворяет уравнению Римана (1) тогда, и только тогда, когда. бД + S^ + a = In л.

Заметим, что если h^ — дзета-подобная функция, то множества Ф1 и Ф₂ (подавно Ф₃ и ФД не более, чем счетны; при этом Ф = Ф_х U Ф₂ и множество Ф^- при 7 = 1,2 может содержать конечное число номеров или даже быть пустым.

Кроме того,

sr - Е

АеФ3

4nfc

1 + 4АГ

V^ of ^ak I 1 ^— ^A ^\

Как легко проверить, sr = 2 V п№. Д\

S™ = 2 У щ. ( Re ( 1) + Re Д— ^Z—^     \    \ Zk )        \ 1 ^— Zi-

АбФ₄    \    \            \ h

Поэтому выражение 5Д +S^ естественно назвать вещественным следом корней функции С(ВП).

Безусловно, самым важным примером дзета-подобной функции является сама дзета-функция Римана. Действительно, согласно формуле (6) из [2; гл. II, стр. 40]

ehz

2Д- 1)Г(1 + f)

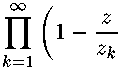
Tk

е

где b = In 2л — 1 — Д 7 — постоянная Эйлера — Маскерони (7 ~ 0,5772) и Zk — все попарно различные нетривиальные нули Дг), т. е., нули отличные от —2m,m = 1,2,... ; все они лежат, как известно (см. [2]), в полосе П.

Согласно результату Харди от 1914 года (см., например, [2; гл. X, и. 2]) множество Ф_х (подавно Ф) для функции Дг) бесконечно. Что же касается множества Ф₂, то согласно знаменитой гипотезе Римана, в случае функции Н^'^ = Д^) оно должно быть пустым. В связи с этим определенный интерес представляет

Теорема 2. Пусть z_k (k = 1, 2,... ) — нуль Дд) кратности п^, лежащий на прямой L: Re z = |. Гипотеза Римана, справедлива тогда, и только тогда, когда. 52^_х р^г = 5, г_Де5:=1 + 1-1п2-11птг.

< Пусть со                                        Г                       1

W o _ ⁿk qW₀ _ ₉ у- °"А- ¹ ~ °"А

1 У'”  2 ~ ДЛ^/Д-Щ-юД где « = „t + bk, „t = 1 We Фз - (1,2... J „ „k e (0.1) At > 0, We ♦,.

Согласно следствию 4 5,¹ + S^Fo = 5. Очевидно, что У = О О S^⁰ = 5. Далее, так как каждое слагаемое в сумме

2 , А 2

АЕФф к к

1 - "к "  (1 - ^)² - А^.

Пк

положительно, то ₅И о ₌ О тогда и только тогда, когда все слагаемые этой суммы отсутствуют, т. е., когда все нули ДД в полосе П лежат на прямой L. >

Доказанный критерий вряд ли можно назвать эффективным. Однако он указывает на одно, принципиально важное, по нашему мнению обстоятельство. Именно, для проверки справедливости гипотезы Римана достаточно знать лишь те (но все те!) нули ДД, которые лежат на L (точнее, достаточно знать значение одной их характеристики, а именно, величины S_X^F°).

Заметим еще, что легко привести пример дзета-подобной функции, для которой гипотеза Римана несправедлива, но которая удовлетворяет уравнению Римана. Для этого достаточно, например, взять любую дзета-подобную функцию, у которой множество Ф2 непусто и содержит конечное число номеров (и, следовательно, УДД — многочлен), причем ^ + ^4-0 = рптг.