О единственности определяющего соотношения для мягких тканей и его значимости для феноменологической термодинамики твердого тела

Предположим, что на экспериментальном уровне материал обладает потенциалом деформации, который является функцией измеренной деформации 8. Обозначив этот потенциал через V(8), запишем связь между напряжением и потенциалом

а =      ,

д8

где с - напряжение, соответствующее измеренной деформации. Предполагая, что эволюция деформаций характеризуется линейной группой преобразований напряжений, получим напряженно-деформированное состояние (с, е) через начальное (с0, е 0) с помощью линейного преобразования оп = ас + ве,

^{0               ,}                                                   (2)

е 0 = ус + 5е, где а в

Y 5

= 1.

Если уравнение (1) справедливо для каждого напряженно-деформированного состояния, то уравнение (2) можно записать в следующей форме dV ^ = а dV ^ ₊ ре d е 0          d е

dV (е) х еп = у —+ 5е. 0

Записанная система позволяет определить потенциал деформации. Действительно, запишем следующее соотношение:

V0 (е 0 ) = J V;(s 0 )dе 0,(5)

где штрих означает производную по указанной переменной. Комбинируя уравнения (4) и (5), получим следующее соотношение:

• Vо(ео) = J(а V,(е)+ PsXyv"(е)+ 5)dе .

Интегрируя соотношение (6), выражая с из формулы (1) через V ' ( е ) и пренебрегая константой интегрирования, получим:

Vо(е о ) = V(е)+ 2 [аУс 2 + 2^се + Р5е 2 ]•

Соотношение (7) показывает существование некоторого инварианта экспериментального напряженно-деформированного состояния. Используя формулу (2), можно показать, что квадратичная форма в выражении (7) имеет следующий вид:

аус2 + 2Русе + р5е2 = с0е0 -се .(8)

Таким образом, выражение (7) принимает вид:

• V0(е 0)-2 с 0е 0 = V(е)-;2 се.(9)

Последнее соотношение можно переформулировать следующим образом:

W (е)= V(е)-72се.

Это должен быть инвариант по отношению к группе линейных преобразований, заданных соотношениями (2).

Данный результат имеет существенное значение, так как показывает, что потенциал деформации может быть определен посредством поиска инвариантов группы преобразований SL (2R). Поиск этих инвариантов представляет собой обычную процедуру с математической точки зрения, однако проблема заключается в определении физического смысла инварианта (10). Физический смысл можно определить из следующих соображений. Энергия диссипации в эксперименте на одноосное нагружение определяется соотношением [1]:

с d е-е d с .                                (11)

С учетом выражения (1) дифференциальная форма (11) принимает следующий вид:

стde-edст = dV(e)-eV"(e)de. (12)

С другой стороны, дифференциал выражения (10) с учетом (1) имеет вид:

2 dW ( e ) = dV ( e ) -e V "(E) d e . (13)

Сопоставляя выражения (12) и (13), получим:

ст d e-e d ст = 2 dW ( e ) , (14) таким образом, в потенциальной энергии дифференциал функции модульного инварианта (10) определяет энергию диссипации в определенном напряженно-деформированном состоянии.

Соотношение (14) отражает результат, который кажется тривиальным и имеет интуитивный смысл. Основываясь на опыте авторов в построении определяющих соотношений, предполагается, что в случаях, когда нет диссипации энергии в материале, он является упругим. Действительно, если в левой части соотношения (14) стоит нуль, то интегрирование дает следующее соотношение:

ст = E e , (15) где Е - константа (модуль Юнга). В этом случае инвариант W ( e ) является константой. С этой точки зрения, упругое состояние, которое характеризуется экспериментальным законом Гука, является недиссипативным.

Твердые материалы, вообще говоря, не соответствуют линейному закону, поэтому можно сделать вывод, что в твердых телах всегда существует диссипация энергии. С математической точки зрения, это означает, что левая часть уравнения (14) не равна нулю. Для этого случая удается объяснить алгебраическую форму функции W ( e ) и, соответственно, потенциала V ( e ) . Мы замечаем, что дифференциальная форма уравнения (14) имеет квадратичный параметр, записанный в следующей форме:

ст d e-e d ст = 2 ( a ст ² + 2 b сте + c e ² ) d т , (16) где a , b и с являются константами, а т является преобразованной дифференциальной переменной.

Соотношение (16) дает существенные характеристики кривой экспериментального нагружения [2]. В результате соотношение (16) можно применять к материалам, имеющим бесконечно малые деформации [3]. Для этих деформаций можно определить физическую основу определяющих законов [4] и возможные соотношения этих законов с внутренним напряженным состоянием материалов [5]. Представленный здесь метод основан на понятии потенциала деформации и позволяет получить некоторые результаты. Кроме того, проведенные рассуждения показывают, что потенциал имеет физический смысл, так как он связан с энергией диссипации.

Дискуссия

Важно отметить в связи с вышесказанным, что мягкие биологические ткани реагируют на нагрузку иначе, чем другие «твердые» материалы. А именно, уравнение (16) указывает некоторое свойство экспериментальной кривой напряжение-деформация: эти кривые имеют гомографическое соотношение между касательным модулем и секущим модулем [4]. Это свойство наблюдалось для мягких тканей Фангом ( Fung ) в работе [6].

Действительно, в случае биологической ткани теория, представленная здесь, не ограничена бесконечно малыми деформациями. Это верно для большого диапазона экспериментальных кривых напряжение-деформация, а во многих случаях это верно для всего диапазона деформации. Важно отметить, однако, что уравнение (16) имеет два основных типа решений, которые ведут к определяющим соотношениям степенного типа и экспоненциального типа [7]. Экспоненциальный тип определяющего соотношения может быть сведен к степенному типу, определяя логарифмическую меру деформации. Поэтому, с энергетической точки зрения, можно сказать, что степенной тип определяющего соотношения есть единственная функциональная форма, которая теоретически допустима. В то же время, если экспериментальные результаты находятся в соответствии с трехмерной моделью напряжений, то определяющее соотношение должно быть гомографическим соотношением между напряжением и деформацией [2]. Такое соотношение может быть получено из экспериментальных данных [8]. Это соотношение влияет на способ описания деформации материалов, в частности, металлов [9], но также показывает, что материалы имеют общие закономерности с точки зрения деформации [10]. Конечно, гомография есть только частный степенной закон для решения уравнения (16), которое не переходит границы предыдущего энергетического формализма. Недавно экспериментальные результаты, подтверждающие это определяющее соотношение, были исследованы Воссуги (Vossoughi) с соавторами [11]. Некоторые полученные экспериментальные факты показывают, что в случае, если степенной закон или экспоненциальный закон применимы, гомографическое определяющее соотношение также применимо.

Главным достоинством в экспериментах по измерению деформации является то, что гомографическое соотношение между напряжением и деформацией может быть определено путем простого рассмотрения данных в трехмерном представлении путем конструирования трех наборов чисел, даваемых экспериментальными напряжениями, экспериментальными деформациями и их произведением. Если точки в пространстве, даваемые этими числами, образуют плоскую кривую (гиперболу), то существует гомография между напряжением и деформацией [2]. Это может быть замечено из рис. 1, на котором приведены данные для портняжной мышцы ( sartorius muscle) , где был использован степенной закон, указанный ниже [12]:

σ= 1,466 ε ^4,293.                                    (17)

Другой пример применения гомографии есть миокард собаки, где использован экспоненциальный закон, указанный ниже [13]:

σ = 24,20 e ^{13,11 ε} - 31,20.                                (18)

Соответствующая геометрическая интерпретация изображена на рис. 2.

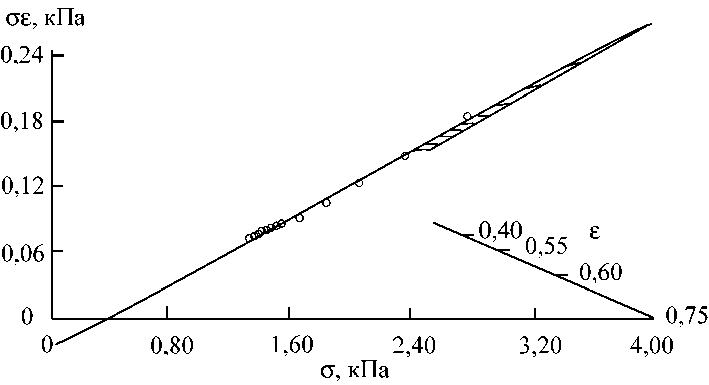
Рис. 1. Гомографическое представление для портняжной мышцы человека

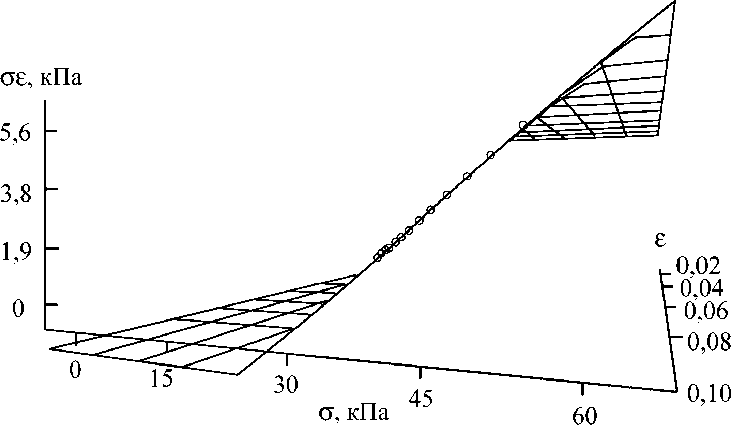
Рис. 2. Гомографическое представление миокарда собаки

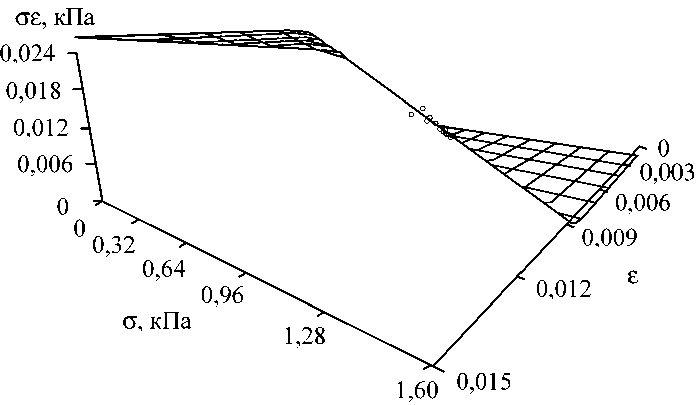
Рис. 3. Гомографическое представление для малоберцовой кости человека

Рис. 1 и 2 показывают, что степенной закон, экспоненциальный закон и гомография действительно перекрываются в экспериментальном диапазоне деформаций. Рис. 3 также иллюстрирует соответствие, используя гомографическое уравнение

7283 s+ 24 o =-----------,

36 s + 29

степенному соотношению Вальбурна-Шнека ( Walburn-Schneck ) [12]

o = 22,58 s 0,6³⁸ .

Точность степенного закона и соответствующая гомография сравниваются с экспериментальными данными [12] на рис. 4.

Кажется, что гомография охватывает данные по напряженно-деформированному состоянию малоберцовой кости человека лучше, чем степенной закон для тех же данных. Имеется, однако, небольшое отклонение теории от экспериментальных данных. Это также имеет место в случае данных для сухожилия хвоста крысы (рис. 5) при сравнении с гомографией вида:

111,31 s- 69,94 o =                  .

172,93 - 10,05 s

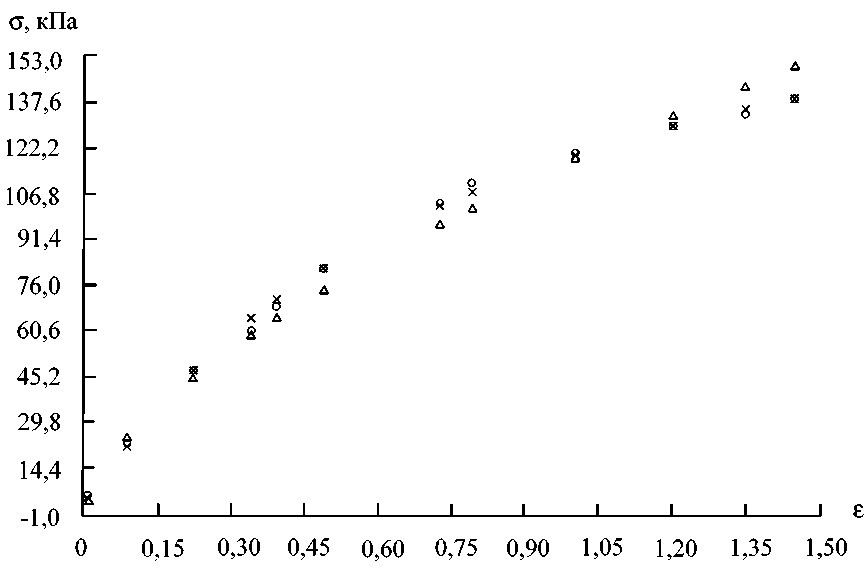
Рис. 4. Сравнение гомографии и степенного закона малоберцовой кости человека (круги – экспериментальные данные, треугольники – степенной закон, крестики – гомография)

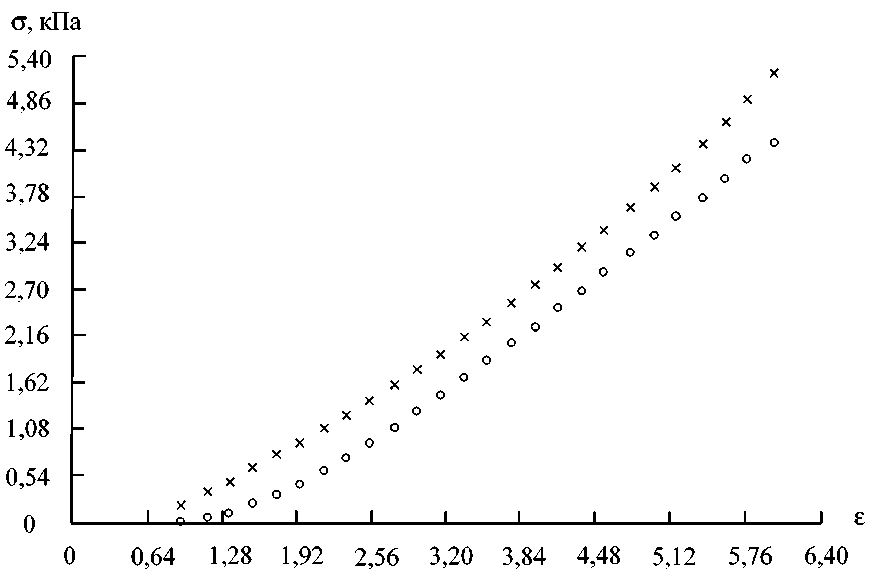
Рис. 5. Данные для сухожилия хвоста крысы (круги – экспериментальные данные, крестики – гомография)

Физической причиной этого является внутренняя структура сухожилия. А именно: в сухожилии хвоста крысы имеются сплетенные элементы, которые должны быть учтены при вычислении начальных напряжений или деформаций. Это легко может быть учтено с помощью экспериментальных данных, находя величину и направление трансляции гомографии, так чтобы добиться совпадения с экспериментальными данными. В случае, изображенном на рис. 5, трансляция является горизонтальной и ее величина равна 0,52. Результат этой трансляции показан на рис. 6. Данный метод учитывает структурную компоненту ткани.

Аналогичным образом на рис. 7 показано применение гомографии для матки свиньи, а на рис. 8 – для артерии свиньи. В случае артериальной ткани свиньи гомография дает вполне точный результат.

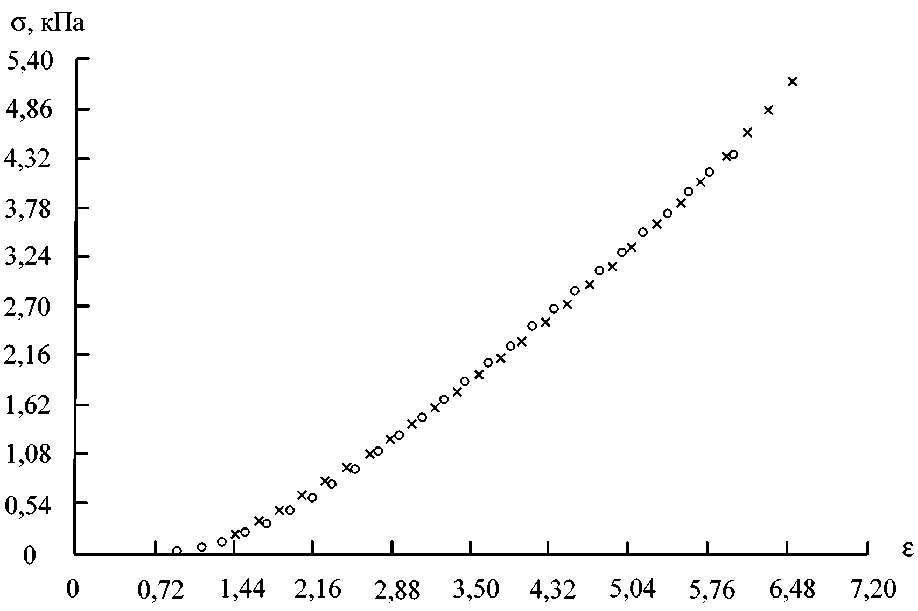
Рис. 6. Данные для сухожилия хвоста крысы (круги – экспериментальные данные, крестики – гомография с трансляцией)

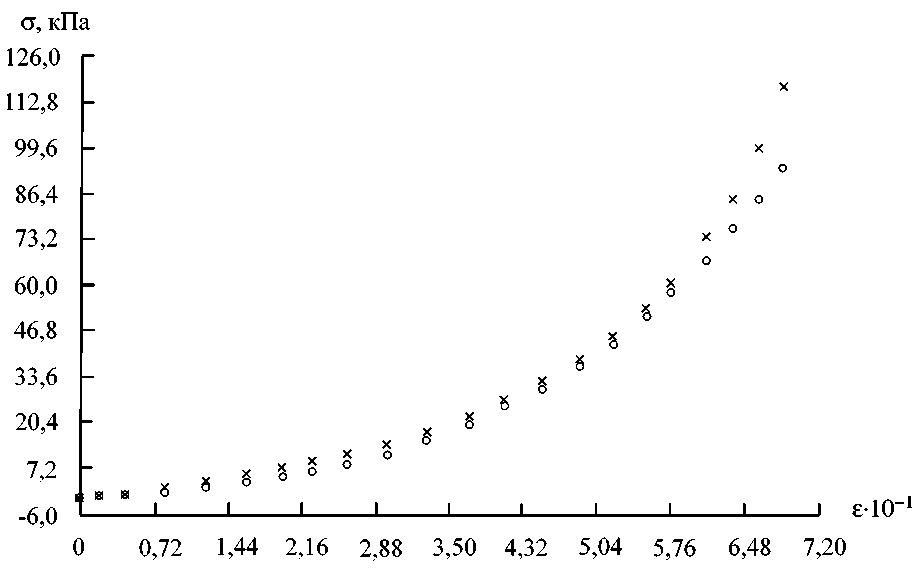
Рис. 7. Матка свиньи (круги – экспериментальные данные, крестики – гомография)

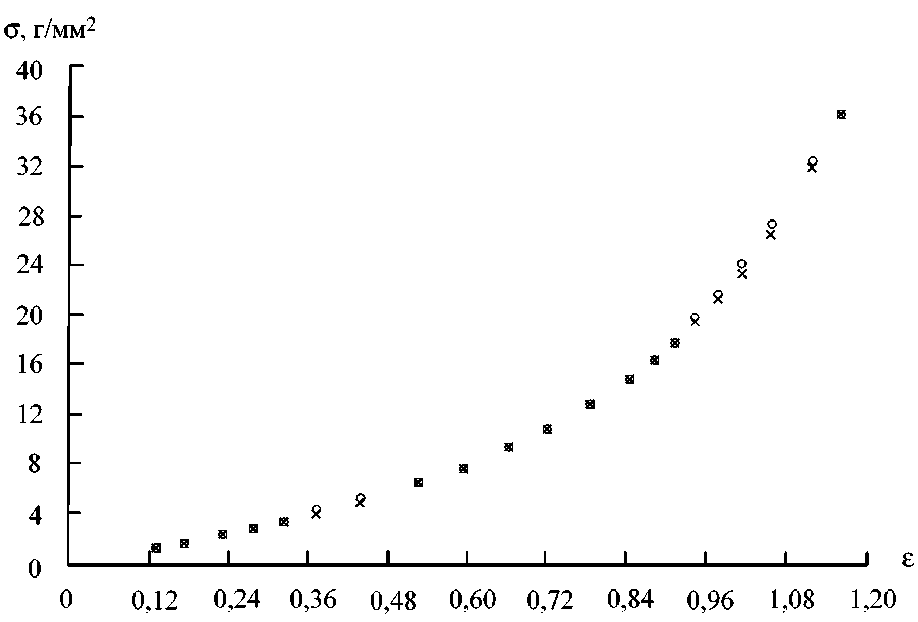
Рис. 8. Артериальная ткань свиньи (круги – экспериментальные данные, крестики – гомография)

Заключение

Уравнения (2) показали, что в окрестности экспериментальной точки ( с ₀, s ₀ ) на кривой напряжение - деформация другие точки могут быть получены путем линейного преобразования. Поэтому с геометрической точки зрения экспериментальные кривые являются траекториями линейной гомогенной группы. Здесь феноменологическая термодинамика твердых тел полностью аналогична термодинамике газов [11]. Однако при дальнейшем анализе можно заметить, что имеется существенное отличие, которое интуитивно кажется вполне ясным, но отчетливый физический закон не имеет математической формы. А именно, твердые тела как материалы имеют память в том смысле, что при начале деформирования из некоторого состояния имеется только траектория деформации, которая допускается внутренним физическим состоянием, совместимым с внешней силой.

Чтобы объяснить это, можно заметить, что если в уравнениях (2) начальное состояние напряжений и деформаций ( с ₀, s ₀ ) взято как переменная величина, то конечное состояние есть переменная величина, получающаяся в результате гомографии [8] с материальными параметрами а , в , У и 5 , которые также являются переменными:

αε + β с =------.

γε + δ

Переменность этих параметров частично связана с изменениями в физической структуре. Поэтому энергия, диссипированная из начального состояния, связана с двумя компонентами:

• энергией, диссипированной в состоянии ( с , s ) , и

• • структурными изменениями при переходе от состояния ( с ₀, s ₀ ) к состоянию ( с , s ) .

Это явление наблюдается в металлах, т.е. связано с теплообменом и повреждаемостью структур. Его также можно наблюдать в мягких тканях, например, мышцы при действиях становятся нагретыми и могут физически повреждаться, если действие мышц соответствующим образом не ограничено или не связано с другими системами. Практическая проблема заключается в том, чтобы найти выражение, которое точно описывает поведение материала. Используя уравнения (2) и (22), мы можем сконструировать выражение, указанное ниже, которое включает две компоненты энергии диссипации:

с0ds0 - s0dс0 = сds - sdс + to1с2 + to2os + to3s2 ,

где to k ( k = 1, 2, 3) представляют собой следующие дифференциальные формы: to , = у d а - а d у ,

to2 = 5dа - аd5 + у dв - вdУ,                          (24)to3 =5 d в-в d5.

Здесь а , в , У и 5 - коэффициенты в уравнении (22).

Уравнение (23) демонстрирует важный результат. Если начальное состояние материала является упругим, то диссипированная энергия равна нулю и левая часть уравнения (23) равна нулю. Тогда, если дифференциальные формы ω _k известны, то состояния, полученные из недиссипативной формы, также определены, будучи полученными путем интегрирования (23). В случае, когда формы ω _k являются точными дифференциалами, фундаментальный степенной закон получается из экспериментальных результатов, как можно увидеть из сравнения уравнений (23) и

• (16). Это указывает, что недиссипативное состояние является особым, в том смысле, что для всех процессов деформации, которые начинаются из этого состояния, компонента энергии диссипации вызывается только структурными изменениями в материале.

Это есть свойство, которое позволяет определить выделение тепла в твердых телах из-за структурных изменений. В этом случае термодинамика твердых тел и газов имеют общность. А именно, в циклических процессах, начинающихся в упругом состоянии, общая энергия диссипации может быть не равна нулю, даже если дифференциальные формы ω _k являются точными дифференциалами относительно некоторого параметра, как в уравнении (16). Другими словами, диссипированная механическая энергия в циклических процессах возникает как результат изменений в физических свойствах, выраженных через напряжение и деформацию, например, пластическую деформацию.

Для газов изменение в физических свойствах является основой теоретической термодинамики. Как неоднократно отмечал Клаузиус ( Clausius ) [14], газы имеют характерное свойство, выражающееся в том, что необратимые изменения в некотором процессе стираются в любом обратимом процессе. Эта идея развита в том смысле, что определение обратимого процесса стало более расплывчатым [15].

В случае твердых тел наиболее очевидной мерой для необратимой деформации является цикл гистерезиса [16]. Уравнение (23) показывает, что в таком цикле сумма энергии диссипации из-за структурных изменений есть константа. Эта константа зависит от материальных параметров α , β , γ и δ . В случаях, когда эта зависимость может стираться, т.е. для газов, энергия диссипации в цикле не зависит от материальных параметров. Однако из этих аргументов можно увидеть, что основные концепции традиционной термодинамики не могут быть непосредственно перенесены на случай твердых тел. Речь идет о температуре, механической работе, теплоте, энтальпии и т.д. Пересмотр этих понятий позволит получить новый взгляд на такие понятия, как деформация, теплоперенос и массоперенос, электромагнитные явления и связанные с этим понятия.

Наконец, уместно заметить, что гомография может служить для построения определяющих соотношений в термодинамических моделях именно для твердых тел. Критерием для развития моделей должно быть и для газов, и для твердых тел сравнение с экспериментальными кривыми. Если экспериментальное определяющее соотношение есть гомография, то циклический процесс можно представить как последовательность зависящих от времени откликов, например, процессы релаксации или ползучести. Эти процессы имеют место при постоянных напряжениях или постоянных деформациях, соответственно, и характеризуются уравнениями, аналогичными уравнению (23), где ω _k являются полными дифференциалами относительно параметра времени [9].

Общие выводы по данной работе заключаются в том, что, с энергетической точки зрения, экспериментальное определяющее соотношение однозначно с точностью до определения меры деформации. Однако для использования экспериментальных результатов необходимо определить конкретный вид степенного закона, т.е. гомографию. Это в особенности иллюстрируется множеством явлений в биологических тканях.

Благодарности

Доктор Конвей рад возможности выразить благодарность Национальной научной ассоциации США (грант CMS 9502123) и ассоциации Уиттекера за частичную поддержку данного исследования. Он также благодарит лабораторию механики и материалов Центральной школы в Нанте (Франция) за дополнительную поддержку данного проекта.