О единственности решения обратной задачи нестационарной фильтрации

Исследованию обратных коэффициентных задач посвящено большое количество работ (см., например, [1, 2]). Особое внимание при этом уделяется доказательству сходимости метода решения и формулировке условий, обеспечивающих существование и единственность решения.

В данной работе формулируются такие условия для обратной задачи фильтрации со смешанными граничными условиями для дифференциального оператора более общего вида, чем в [1].

• 1.    Постановка прямой задачи

Процесс нестационарной фильтрации жидкости к одиночной скважине в осесимметричном случае описывается уравнением dp _ 1d L dp 1                        m dt рдр \_раРр^ др]’                              ()

где p = p(p, t) — давление в пласте, ст = ст(р) - коэффициент гидропроводности.

Решение уравнения (1) будем искать в области изменения переменных (р, t) : t >  0 , 0 < r ₀ <  р <  r .

Сделаем следующие предположения:

• а)    известно начальное давление в пласте

Р(р, 0) = Ро;

• б)    на границе пласта выполняется условие «непротекания»

dp(^,^)=0, t > 0;

∂ρ

• в)    известно забойное давление

• 2.    Постановка обратной задачи

Р(г0,^ = fl(t), t > 0-

Предположим, что коэффициент гидропроводности а(р) удовлетворяет условию

а(р) >  d > 0 при р G [r ₀ ,r].

Задачу (1) – (4) называют прямой задачей фильтрации. При известной функции а(р) , удовлетворяющей условию (5), и при дополнительных предположениях о гладкости функций а(р) , f 1 (t) и p(p,t) эта задача имеет единственное решение.

Обратная задача заключается в определении неизвестного коэффициента а(р) в уравнении (1) по дополнительной информации о решении задачи (1) - (4).

Предположим, что нам известен дебит скважины dP(ro,t)

= g^                         (6)

где g(t) - ограниченная и непрерывная функция, t >  0 .

Так как при неизвестной функции а(р) решение p(p,t) задачи (1) - (4) также неизвестно, то обратную задачу сформулируем как задачу определения двух функций а(р) и р(р, t) , удовлетворяющих условиям (1) - (6).

Сделав в задаче (1) - (6) замену переменной u(p,t) = р(р, t) — po, перейдем к новой задаче du=11 и^ du 1,

∂t ρ ∂ρ ∂ρ

* 0)=0,

du(r,t)    п
др       ,	(9)

u(r0,t) = f (t), du(r0,t)

д     = g(t), где 0 < ro < р < r, t > 0, f (t) = fi(t) — po.

Будем предполагать, что функция f (t) G C2[0, то) удовлетворяет условиям f (0) = f'(0) = 0, f (t) = 0 при t > to, f (t) ^ 0 при t > 0, а функция a(p) удовлетворяет условию (5) и а(р) G C2[ro,r].

Определение 1. Решением обратной задачи (7) - (11) назовем пару функций а(р) и u(p,t) таких, что а(р) удовлетворяет условиям (5) и (13), и(р,Р) имеет непрерывные частные производные (и(р, t), и'р(р, t), и^р(р, t), и'1(р, t) G C[(r0,f) х (0, то)]), функции a(p) и u(p,t) удовлетворяют уравнению (7), а функция u(p,t) удовлетворяет условиям (8) – (11).

Лемма 1. Если выполнены сформулированные выше условия, то при t ^ то u(p, t) ^ 0, u p (p,t) ^ 0, u t (p, t) ^ 0 и Рдр [ р^ ( р ) ^dP^ ] ^ 0 равномерно на отрезке [r o ,f].

Доказательство. Пусть a(p) и u(p,t) — решение обратной задачи (7) - (11). Тогда ввиду того, что f (t) = 0 при t >  t ₀ , функция u(p, t) для t >  t ₀ является решением следующей задачи:

∂u ∂t

1 dr , . du pdpM^p) dp

0 < r ₀ <  p <  r, t >  t ₀ ,

u(r o ,t) = u' p (r,t) = 0, t >  t 0 ,

u(p,t0) = d(p), r0 < p < r, где ^(p) G C 1[r0,r], d(r0) = dPr) = 0.

Используя для решения этой задачи метод разделения переменных (u(p, t) = y(p)v(t)), получим, что u(p,t) = ^Щ ^«) Уп«) 'd') e n=0 P-Pro                    7

^A n W),

где A n >  0 и y _n (p) — собственные значения и нормированные собственные функции задачи Штурма-Лиувилля

^[p^⁽p⁾y ^{, (}p^{)] /} + ^Apy⁽p) = ⁰, У(г 0 ) = У (r) = 0.

Покажем, что собственные значения A n > 0 при n >  0 . Так как предполагается, что A n >  0 упорядочены по возрастанию, то достаточно показать, что А ₀ > 0 (А ₀ = 0) .

Предположим противное, A ₀ = 0 . Тогда

	( p^(p) у 0 (p) ) ' = 0,                                      (16)
а	У 0 (г 0 ) = 0, у 0 ( гР = 0.                                    (17)
Из (16) следует, что	p^(p) у 0 (p) = C i ,
и второе из условий (17)	влечет C 1 = 0 . Поэтому y 0 ( p ) = 0 ,                                          (18)
и значит,	y 0 (p) = C 2 .

Используя первое из условий (17), получим, что C 2 = 0 , а у о (р) = 0 , что противоречит условию нормировки собственных функций у _п (р) . Таким образом, A n > 0 для n >  0 .

Из положительности собственных значений λ n и разложения (14) следует утверждение леммы.

Введем функцию переменной t

V(р, s) , являющуюся преобразованием Лапласа от и(р, t)

по

о га

V ⁽ р^{,s )} = /

e st u^t) dt.

На основании леммы 1 из (7) – (10) следует, что для значений комплексного параметра s таких, что Re s >  s o > 0 , функция V (р, s) является решением краевой задачи

Р И^Р - sV = ^0,

W.s) = 0,

V (r o ,s) = V ^{( s )}

га где ^(s) = f e^ff (t) dt. Кроме того функция V(р, s) удовлетворяет дополнительно-0

му условию

V ' (r o ,s) = Ms),                                   (22)

га где ^(s) = J e-stg(t) dt.

Рассмотрим функцию W(р, s) , являющуюся решением задачи Коши для уравнения (19) c краевыми условиями

W(r, s) = 1, W; (f, s) = 0.

Так как функции V(р, s) и W(р, s) являются решениями дифференциального уравнения (19) и V ' (f, s) = W ' (f, s) , то из теоремы [3, с. 179] следует, что они линейно зависимые, то есть

V(р,s) = C(s) W(р,4

Тогда из (21) и (24) следует, что

^(s) = C(s) W(ro,s), а из (22) и (24) следует, что

M(s) = C(s) W'(ro,s).

Из последнего равенства можно выразить C (s) :

C(s) = IV4

^W ' ⁽r o ^,s)

Лемма 2. При сформулированных выше условиях множество нулей функции W (r ₀ , s) не пересекается с множеством нулей функции W'_p(r ₀ ,s).

Доказательство. Предположим противное, то есть найдется s ₀ такое, что

W (ro,So) = wp (ro,So) = O.(28)

Тогда W(р,so) является решением задачи Коши для уравнения (19) и начальными условиями (28). Следовательно, для любого р Е [ro, ■] W(р, so) = 0, что противоречит условию W(r,s0) = 1.□

Рассмотрим дифференциальное уравнение

• -1 [р^(р) у'^ = А У(Р).

ρ с краевыми условиями

y(ro) = 0, y'(r) = 0

или

Wo) = 0, y'(r) = 0.

Лемма 3. При сформулированных выше условиях значения s = s ₀ и s = S o являются, соответственно, нулями функций W(r ₀ ,s) и W '_p (r ₀ ,s) тогда и только тогда, когда числа А ₀ = — s ₀ и А ₀ = — S o являются собственными значениями задач Штурма-Лиувилля (29), (30) и (29), (31).

Доказательство. Так как функция W(р, s q ) является решением уравнения (19) с s = S 0 , то функция У о (р) = W(р, s o ) является решением уравнения (29) с А ₀ = — s g . Второе краевое условие в (30) для у ₀ (р) следует из (23), а первое из того, что s ₀ является нулем функции W (r ₀ , s) . Таким образом, у ₀ (р) является решением задачи (29), (30). Это решение нетривиальное, так как в силу (23) y ₀ (r) = W(r, s ₀ ) = 1 . Следовательно, λ 0 является собственным значением задачи (29), (30).

Очевидно, что справедливо и обратное утверждение. Действительно, если λ ₀ является собственным значением, а У о (р) - собственной функцией задачи (29), (30), то на основании первого из условий (30) значение s 0 = — А 0 является нулем функции W (r o , s) .

Теперь предположим, что s = s o является нулем функции W _p (r ₀ ,s) . Тогда из того, что функция W(р, 8 0 ) является решением уравнения (19) с s = s g , следует, что функция У о (р) = W(р, s 0 ) является решением уравнения (29) с А ₀ = — s g . Второе краевое условие в (31) следует из (23), а первое - из того, что s o является нулем функции И"(r o ,s) .

Таким образом, у ₀ (р) является решением задачи (29), (31). Это решение нетривиальное, так как в силу (23) 'y o (r) = W (■, s o ) = 1 . Следовательно, А ₀ является собственным значением задачи Штурма-Лиувилля (29), (31).

Обратно, если А ₀ является собственным значением, а у д (р) - собственной функцией задачи (29), (31), то s o = — А ₀ на основании первого из условий (31) есть ноль функции W p (r ₀ ,s) .                                                              □

Предположим теперь, что функция а(р) Е C ² [r ₀ , /■ ] удовлетворяет условию (5), и ^(г) = 0 . Вернемся к решению W(р, s) задачи Коши (23) для уравнения (19).

Лемма 4. При сформулированных выше условиях на функцию а(р) функции W (р, s) и W ' (р, s) для каждого фиксированного р Е [r ₀ , r] являются целыми функциями комплексного параметра s.

Доказательство. Применяя преобразование Лиувилля ( [4], с.35) к уравнению (19), заменим функцию W(р, s) на функцию z(x, s) , определяемую параметрически следующим образом:

ρ

x =

i гр   de c Jr0 v^(e),

r 0

где

1 r

c =

i г de

^П Л V o(l) ’

r 0

а x – новая независимая переменная, и z(p,s) = VpCT 4 (p) W (р,s).

Подставляя выражения (32) – (34) в уравнение (19), приведем его к уравнению

д ² z              ₂

-—; + a(x) z — c ² sz = 0, 0 <  x <  n, dx ²

где

c задается формулой (33), а

1 d ² 9(x) ^a(x) = — 9(x) "dx²" ¹

где

9 = 9(x) определена параметрически формулой (32) и равенством

⁹⁽Р) = VP^{a 4 (} р).

и

Теперь сделаем замену в краевых условиях (23):

z(n, s) = V r СТ ⁴ (r)

^z X ^(n,s) = /, ст ^{4 (r)}.

Далее введем новую переменную т = п — функции w(t, s), которую определим формулой

x и перейдем от функции z(x,s) к

w ( t, s) =

e >r v CT(r) +    ■ „ '

z(n — t, s).

Используя формулу (40), легко проверить, что функция w ( t, s) удовлетворяет уравнению

d 2w      ,       .        9

- + a(n — т ) w — c ² sw = 0, 0 <  т <  n. дт ²

При этом условия (38) и (39) для функции w ( t, s) будут выглядеть следующим образом:

w(0, s) = sin a,

а

w T (0, s) = — cos a,

где

a = arcsin

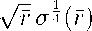
rv^r+ ' .

Из теоремы [5, с. 14-15] следует, что для каждого фиксированного т Е [0, п] функции w ( t, s) и w T (т, s) являются целыми функциями s , а из формул (34) и (40) будет следовать утверждение леммы.

Так как функция W(р, s) представляет собой решение уравнения (19) с условиями (23), то из леммы 4 следует, что W(р, s) и W p (р, s) при фиксированном ρ являются аналитическими функциями комплексного переменного s во всей комплексной плоскости.

В дальнейшем всюду будем предполагать, что а(р) Е C ² [r ₀ ,r] , ^( r) = 0 и выполняется условие (5).

Пусть a _i (р) и u i (p,t) (i = 1, 2) - решения обратной задачи (7) - (11). Обозначим через V _i (р, s) преобразование Лапласа от u i (p,t) , а через W i (p, s) — решения задачи Коши для уравнения (19) с а(р) = a _i (р) и начальными условиями (23). Для краткости (W i (p, s)) P | _p = _r 0 будем обозначать W/ (r ₀ ,s) .

Из (10) следует, что V i (r ₀ ,s) = V ₂ (r ₀ ,s) . Тогда, используя формулы (24) и (27), получим, что при Re s >  s ₀ > 0

W i (r o ,s) = W 2 (r 0 ,s)

W 1 (r 0 ,s)    W 2 (r 0 ,s)'

Из леммы 4 следует, что функции W i (r 0 , s)/W/(r 0 , s) при i = 1,2 являются аналитическими функциями комплексного переменного s во всей комплексной плоскости за исключением нулей W ' (r 0 , s) , являющихся особыми точками.

Из (45) следует, что нули и особые точки функций W ₁ (r ₀ , s)/W { (r ₀ , s) и W ₂ (r ₀ , s)/W 2 (r ₀ ,s) совпадают.

Используя лемму 2, окончательно получим, что все нули функций W i (r 0 , s) и W ₂ (r 0 , s) совпадают, и все нули функций W-^^s) и W 2 (r 0 ,s) также совпадают.

Таким образом, на основании леммы 3 для любого n выполняются соотношения

АП = АП

и i2 ^ n ^П , где {АП} при i = 1, 2 - все собственные значения задачи Штурма - Лиувилля (29) - (30) с а(р) = ai(р), упорядоченные по возрастанию, а {АП} - все собственные значения задачи (29), (31) с а(р) = ai(р), также упорядоченные по возрастанию.

Теорема 1. Предположим, что функция f (t) удовлетворяет условиям (12). Тогда, если ^(р) и u _i (р,t), i = 1,2 - решения обратной задачи (7)-(11) такие, что ^ 1 ^(r) = ^ 2 ^(r) = ^ 1 ^(r 0 ) = ^ 2 ^(r 0 ) = ⁰, J r -d= = J r /\, а ^также a i ⁽ r 0 ) = a 2 ⁽r 0 ) = ^r 0 yai ( £ )        ^r 0 y^2 ( ^ )

^ ₁ (f) = ^ ₂ (r), и значение ^(r ₀ ) нам известно, то а ₁ (р) = а ₂ (р) для р Е [r ₀ ,f] и u 1 (р, t) = u 2 (р, t) для р Е [r 0 , rr], t >  0

Доказательство. Сделав в уравнении (29) замену переменных Лиувилля (32), (33) и z(p) = ^Ра 4 (p) У(Р),                                 (48)

перейдем от функции y i (p, А) к функции z i (x, А) , удовлетворяющей уравнению

-   ,i + q i (x) Z i = c ² Xz i , 0 <  x <  п, i = 1, 2,                     (49)

dx ²

где функции qi(x) = —ai(x) определяются формулами (32), (33), (36), (37) и являются непрерывными на отрезке [0,п]. Сделав еще одну замену wi(T, А) = zi(n — т, А), т = п — х, 0 < т < п, i = 1, 2, получим уравнение для функции wi^, А)

• ^d2wi .    /        X            А                                л

  
  

+ q i (n — т ) W i = c А W i , 0 <  т <  п, i = 1, 2. дт ²

Теперь преобразуем граничные условия (30) и (31). Получим, что условиям (30) соответствует пара граничных условий

W i (п,А)=0, i = 1, 2,                                 (51)

w i (0, А) cos(e) — w i (0,А)sin в = 0, i = 1, 2,                      (52)

где

в = arcsin

(^Х* (»)²"W)

и 0 < в <  П .

Условиям (31) соответствуют граничные условия (52)

и

w i (n, А) cos( y ) — w'i(n, А) sin y = 0, i = 1, 2,                       (53)

где y = arcsin ^1 j ^ 1 + ^ 2 ^ 0 ^ a(r g )

и 0 <  y <  П .

Таким образом, задача Штурма – Лиувилля (50) – (52) порождает возрастающую последовательность собственных значений { µ ⁱ _n } . При этом из формулы (46) и условий теоремы следует, что для любого n

P n = P n .

Аналогично, задача Штурма – Лиувилля (50), (52) и (53) порождает возрастающую последовательность собственных значений { р П } такую, что на основании (47) и условий теоремы следует, что для любого n

• ¹       //.²

  
  

^р п   ^р п

Из теоремы, приведенной в [6], и равенств (54) и (55) следует, что для любого х G [0, п]

а 1 (х) = а ₂ (х).                                           (56)

Таким образом, обозначив ai(x) через a(x) и воспользовавшись формулами (36) и (37), получим, что i (x + a(x) 9i (x) = 0, i = 1, 2, d x2

где

9i(0) = Vro a 4 (ro)

и

9 (0) = ,        4 (ro).

• 2    r o

Задача Коши (57) – (59) для линейного дифференциального уравнения второго порядка имеет единственное решение, и, следовательно,

9 1 (x) = ^ 2 (x).

Используя формулу (37), получаем, что ai(p) = a2(p) при p E [ro,f].

Но тогда и решения прямой задачи (7) – (10) при соответствующих ограничениях на функции ui(p,t) и f(t) будут при любых значениях p E [r0,f] и t > 0 удовлетворять условиям и1(Р<Ь) = u2(P,t), что и доказывает теорему.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (грант р_урал_а №10-01-96000).