О факторизации $ (\ mathbb {B}, p) $-суммирующих операторов

Символом PrtCT := PrtCT(B) обозначим множество всех счетных разбиений единицы в B. Пусть E - банахова решетка, Y - B-циклическое банахово пространство. Для произвольного линейного оператора T Е L(E,Y) положим по определению n               1/p ap(T) := sup     inf sup ( V|kkTxikp)

( n k)ePrt_CT k _eN \i=i

xi,..., xn Е E,

n

II X ^|xi|^ i =1

6 1, n Е N

ОПРЕДЕЛЕНИЕ 2. Оператор T Е L(E, Y) называется (B,р)-суммирующим, если ap(T) < то. Таким образом, T является (B,p)-cyммиpyющим тогда и только тогда, когда существует константа. C > 0 такая, что для любо го копенного набора. x1,... ,xn Е E найдется счетное разбиение единицы (nk) Е PrtCT(B), для которых выполняется соотношение n              1/p

n

|xi| i=1

sup У? knk Txikp)   6 C k∈N

Как видно, если р = 1, то приходим к определению B-суммирующего оператора, введенному в [1, определение 7.1], см. также [4, определение 5.13.1].

Определение 3. Пусть E — банахов а решетка, B — некоторая полная булева алгебра проекторов в L(E) единичной нормы. 1 6 р < то. Норма, k • k в E называстся (B,p)-cy-пераддитивной, если выполняется соотношение inf sup (knkx||p + knkykp)1/p 6 ||x + yk

Можно показать, что норма в банаховой решетке E будет (B,p)-cyпepaддитивнoй тогда II только тогда, когда для любых x1,...,xn Е E+ выполняется n             1/p inf sup I Y^kkxi kp 1   6 kx1 + ••• + xnk-

⁽ n k )e^prt _CT k _eN у i=1

Все уже готово, чтобы сформулировать основной результат настоящей заметки, но прежде рассмотрим два примера банаховых решеток с (B,p)-cyпepaддитивнoй нормой.

ПРИМЕР 1. Пусть E - банахова решетка с р-супераддитивной нормой. (П, Е, д) - про странство с мерой. Рассмотрим U”(E ) - пространство измеримых по Бохнеру вектор-функций f со значениями в E, у которых поточечная норма |f | : t ^ k f (t) k (t Е П) при надлежит L^k). Введем норму в U”(E ) по формуле k f k := k If Ilk- В1° k ¹ Ik ^— норма в L~(д). Обозначим через B булеву алгебру всех характеристических функций измери мых множеств. Тогда U”(E ) бутет B-тщклпчоской банахов.>й решеткой. Норма в L ^( E ) будет (B ,p )-cyпepaддптпвпoй тогда, п то.тько тогда, когда, норма, в E р-еупсрадднтпвна.

Пример 2. Пусть Q — экстремальный компакт, E — банахово решетка. Обозначим символом C^(Q,E) множество классов эквивалентности непрерывных вектор-функций, действующих из кототпих множеств dom(u) С Q в E. Напомним, что множество в топологическом пространстве называют котои^м, если его дополнение является тощим. Множество C^(Q,E) можно естественным образом снабдить структурой модуля над кольцом C^(Q). Более того, непрерывное пр<щолжеиие поточенной нормы t ^ kf (t)k (t Е dom(f). f Е C^(Q,E)) определяет раздожимую норму |J iia C^(Q,E) co значениями в C^(Q). Введем щюстраиство C#(Q,E) := {f Е C^(Q,E) : |f| Е C(Q)} ii ному в нем ||f k := |||f|k^. Обозначим через B булеву алгебру всех характеристических функций открыто-замкнутых подмножеств множества Q. Тогда C#(Q,E) будет В-цпклшюской банаховой решеткой. Норма в C#(Q,E) будет (В,р)-супераддптпвной тогда в только тогда, когда норма в E р-супераддитивиа.

Теперь приведем формулировку и доказательство нашей факторизационной теоремы.

Теорема. Пусть E — банахова решетка, Y — В-циклическое банахово пространство. Оператор T Е L(E,Y ) является (Вурфсуммирующим тогда и только тогда, когда существуют главный идеал В_о в В. В_о- циклическая ба.пахова решетка. F (• (В₀ ,р )- супераддитивной нормой, решеточный гомоморфизм Q : E щ F с В₀-плотным образом в FiI Вщлиисйпый оператор S Е L(F, Y ) такие, что

T = SQ, |S| 6 | 1 k, |Qk 6 ap(T ) .

C Достаточность. Так как в сякое разбиение единицы в Во может быть дополнено до разбиения единицы в В, то в определении 2 достаточно ограничиться разбиениями единицы в В_о. Памтв ( n k) - произвольное разбпенпе единицы в В_о. x1, ... ,x n Е E. Тогда в силу В₀-лппойпости S 11 (В₀,р)-супораддптпв1 юстн нормы в F выполняются соотноше ния

/ n               1/р sup ( V knkTxikp )

k ∈ N

n                   \ 1/p

= sup ( V |S (nk Qx i )kp ) k eN \i=1

6 sup k∈N

n                 1/p kπk|Qxi|kp i=1

n

|Qxi| i=1

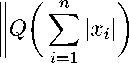
6 U p (T)

n

|xi| i=1

Следовательно, оператор T является (В,р)-суммирующим.

Необходимость. Ввиду [2, теорема 7.3.3(1)] отождествим (Y, || • ||) с bo-полным пространством (Y, |-1, Л), нормирующая решетка которого Л служит порядново полным AM-пространством с единицей 1. причем |y| = || |у 1U (у Е Y). г де || • U - равномерная норма, в Л. Более того, множество всех порядковых проекторов в Л изоморфно полной булевой алгебре В. В дальнейшем мы будем отождествлять эти булевы алгебры. Определим оператор р : X щ Л+. полагая n           1/p                        n

р(х) := sup < I У^| Txi |^p I : x1,..., x n Е E, X |x i | 6 |x|, n Е N    (x Е E ).

i =1                                   i =1

Супремум в указанной формуле существует, так как ввиду [5, лемма 5.1] и (В,р)-сум-мируемости оператора T выполняете я условие (P^J Txi|^p) / 6 a_p(T )||x||l для всех x 1 ,...,xn Е E, ^рп 1 |xi| 6 |x|. Покажем, что р : X щ Л является полунормой. Ясно, что р ( Ах ) = | А | р ( х ) для всех x Е X и А Е R. Па -ств z1 ,...,zn,x,y Е E такие, что ^рп =1 |zi| 6 |х + у|. в силу [3, Broposition 1.1.3] найдутся ui, vi (i = 1,... ,n) из E₊ такие, что |zi| = ui + vi (i = 1,... ,n), Pⁿ =1 ui 6 |x|, Pⁿ =1 vi 6 |y|. Из неравенства Минковского следует справедливость соотношений

^X |Tv iF )^1/P > (XX(ITu il + |Tv i l) p )^1/p

р^{(х) +} р⁽у) > (XITu ilp ) /р ⁺ ( i =1

n

> (X(| Tui + Tvi i =1

I )p)1/p

n

= ( ElTzilp)

i =1

1 /p

Переходя к супремуму по всем z 1 ,..., z n G E, ^2П =1 | z i| 6 | x + у |, пол учим p(x) + p(y) >  p ( x + у). Ясно, что из соотношения | x | 6 | у | еле дует p(x) 6 p ( y). Поэтому множество p-1(0) := {x g E : p(x) = 0} является равномерно замкнутым порядковым идеалом в E. Обозначим фактор-рсшстку E/p ^-1 (0) не_Г>сз F₀ п пз-отв Q : E ^ F₀ - канонический фактор-гомоморфизм. Определим норму на F₀ по формуте k Qx k := ||p(x )|U (x G E ). Тогда ( F ₀ ,p, Л) - решетонно нормированияя решетка. Из определения p ii [5. лемма. 5.1] следует справедливость соотношений