О феноменологической теории магнитных бурь
Автор: Гульельми А.В.
Журнал: Солнечно-земная физика @solnechno-zemnaya-fizika
Статья в выпуске: 2 т.2, 2016 года.
Бесплатный доступ
В данной статье рассмотрены методические вопросы моделирования D st-вариации геомагнитной бури. Описана так называемая модель RBM (Russell - Burton - McPherron), имеющая вид обыкновенного дифференциального уравнения, решения которого имитируют связь D st-вариации с азимутальной компонентой межпланетного электрического поля. Особое внимание обращено на пороговый характер возбуждения D st-вариации. Указано на необходимость стохастического обобщения модели RBM путем учета флуктуаций, присущих любой физической системе. Дано интегральное представление бифуркационной диаграммы D st-вари-ации. Это позволило учесть влияние флуктуаций, которые устраняют корневую сингулярность диаграммы и приводят к смещению пороговой точки. Показано, что D st-вариация принадлежит к широкому классу пороговых явлений, родственных фазовым переходам второго рода. Проведена аналогия с пороговыми явлениями в магнитосфере, атмосфере и литосфере Земли. Кратко рассмотрены вопросы о мягком и жестком прохождении физических систем через порог, а также о взрывной неустойчивости в геофизических средах.
Магнитосфера, фазовый переход, бифуркация, флуктуации, взрывная неустойчивость, атмосфера, литосфера
Короткий адрес: https://sciup.org/142103599
IDR: 142103599 | УДК: 550.3 | DOI: 10.12737/18126
Текст научной статьи О феноменологической теории магнитных бурь
Под воздействием солнечного ветра и межпланетного магнитного поля с удивительным постоянством происходят обычно плавные, а иногда и резкие изменения состояния магнитосферы Земли. В данной статье рассматривается один пример таких изменений, причем в самом упрощенном виде. Речь пойдет о магнитной буре. Внимание будет сосредоточено на шторм-тайм-вариации (сокращенно D st ), которая представляет собой важнейшее проявление магнитной бури [Нишида, 1980].
Феноменологическая теория Dst-вариации предложена в работе [Burton et al., 1975]. Она имеет вид обыкновенного дифференциального уравнения первого порядка, решения которого имитируют связь Dst-вариации с азимутальной компонентной межпланетного электрического поля. Будем сокращенно называть данное уравнение моделью RBM (Russell — Burton — McPherron), как это было сделано в монографии [Guglielmi, Pokhotelov, 1996]. В статье [Гулье- льми, 1988] внесено уточнение в модель RBM, а в статье [Гульельми и др., 1989] представлено экспериментальное обоснование предложенной модификации.
Модель RBM относится к типу так называемых игрушечных моделей (toy models), которые широко используются в теоретической физике и астрофизике для описания особо сложных и/или не до конца понятных процессов. Сложность магнитной бури не требует особых пояснений. Эта сложность уже сама по себе оправдывает использование феноменологической редукции и предельно простых математических средств для того, чтобы формализовать наблюдения, не вводя немотивированных гипотез ad hoc. Но в дополнение к сложности существует еще и не до конца решенная проблема, а именно проблема пересоедине-ния (reconnection) межпланетных и геомагнитных силовых линий. В процессе пересоединения зарождаются источники кольцевого тока, создающего Dst-вариацию [Нишида, 1980]. Физика пересоединения далеко не во всем понятна [Goldstein, 2001], но феноменология пересоединения сравнительно проста [Дан- жи, 1961]. Это обстоятельство в свое время и дало возможность построить модель RBM.
Предлагаемая статья является методической и дискуссионной. Раздел 1 посвящен описанию модифицированной модели RBM. При этом обращается особое внимание на пороговый характер возбуждения D st-вариации. В разделе 2 указано на необходимость стохастического обобщения модели RBM путем учета флуктуаций, воздействующих на процесс формирования D st-вариации. В разделе 3 дано интегральное представление бифуркационной диаграммы источника кольцевого тока. Это позволило простым путем учесть влияние флуктуаций, которые устраняют корневую сингулярность в пороговой точке. В разделе 4 показано, что D st -вариация принадлежит к широкому классу пороговых явлений, родственных фазовым переходам второго рода. Проведена аналогия с пороговыми явлениями в магнитосфере, атмосфере и литосфере Земли. Кратко рассмотрен вопрос о мягком и жестком прохождении физических систем через порог, а также затронут вопрос о взрывной неустойчивости в геофизических средах. В разделе «Заключение» кратко перечислены результаты анализа.
1. МОДЕЛЬ RBM
Модифицированная модель RBM выглядит следующим образом. Пусть E ( t ) — азимутальная компонента межпланетного электрического поля, а q ( t ) — источник кольцевого тока, ответственного за D st -вариацию, причем q≥ 0. Вместо D st удобно использовать величину
D=a+bp1/2–Dst, (1) пропорциональную интенсивности кольцевого тока. Здесь p — динамический напор солнечного ветра. Числовые значения параметров a и b далее не потребуются. Эволюция D(t) описывается уравнением dD/dt=q–D/τ, (2) где τ — время распада кольцевого тока. С точностью до коэффициента пропорциональности зависимость q от E имеет следующий вид: q=0, если E Введем потенциал U(q, E) и рассмотрим динамическую систему dq/dt=–¶U/¶q, (3) которая позволит метафорически понять происхождение зависимости q от E. Переопределим размерности t и q таким образом, чтобы не загромождать изложение ненужными здесь коэффициентами пропорциональности, и положим U=(Ec–E) q2/2+q4/4. (4) Рис. 1. Зависимость источника Dst-вариации геомагнитного поля от азимутальной компоненты межпланетного электрического поля в рамках модифицированной модели RBM Напомним, что в теории фазовых переходов и в теории катастроф величину q называют параметром порядка, величину E — управляющим параметром, а значение E=Ec — точкой бифуркации (см., например, [Гилмор, 1984]). Зависимость q(E) иногда называют бифуркационной диаграммой. Нетрудно убедиться, что в равновесном состоянии из (3), (4) вытекает зависимость q от E, на которую указывалось выше. В самом деле, при E<Ec существует одна точка равновесия q=0, и она устойчива. С ростом E происходит бифуркация, и при E>Ec возникают две точки равновесия, причем точка q=0 неустойчива, а точка q=(E–Ec)1/2 устойчива. Видно, что параметр порядка равен корню квадратному из надкритичности. Для сравнения укажем, что в классической модели RBM зависимость q от E линейна при E>Ec [Burton et al., 1975]. В рамках динамического описания (3) линейная зависимость получается, если второй член в правой части (4) заменить на q3/3. Тогда динамическая система (3) будет обладать не кубичной, а квадратичной нелинейностью. Теоретически это возможно, однако выбор потенциала (4) лучше соответствует данным наблюдений [Гульельми и др., 1989].
2. О ФЛУКТУАЦИЯХ Итак, зависимость q от E имеет пороговый характер. Из теории динамических систем известно, что с приближением к порогу возрастает роль флуктуаций, присущих любой реальной системе [Гилмор, 1984; Horsthemke, Lefever, 1984]. Есть две причины, по которым следует сделать стохастическое обобщение модели RBM и рассмотреть влияние флуктуаций на бифуркационную диаграмму в окрестности пороговой точки. Во-первых, флуктуации сгладят порог и тем самым устранят физически неоправданную сингулярность функции q(E) в точке E=Ec. Во-вторых, флуктуации, вообще говоря, сместят порог. Это обстоятельство надо учитывать при интерпретации измеренных на опыте значений величины Ec. При поиске стохастического обобщения модели RBM возникает вопрос, какое из двух основных уравнений — (2) или (3) — представляет наибольший интерес с точки зрения поставленной выше задачи. Вполне понятно, что учет флуктуаций в нелинейном уравнении (3) интереснее, чем в линейном уравнении (2). Рассматривая уравнение (3), зададим себе второй вопрос: какого рода флуктуации — аддитивные или мультипликативные — следует выбрать для анализа прежде всего? Если выбрать модель с аддитивными флуктуациями, то к правой части уравнения (3) следует добавить источник Лан-жевена. Происхождение такого источника флуктуаций не вполне ясно. Введение источника Ланжевена было бы типичной гипотезой ad hoc. В то же время идея о существовании мультипликативного источника не требует дополнительных гипотез. Она естественно вытекает из структуры потенциала U(q, E). В самом деле, управляющий параметр E испытывает флуктуации, связанные с наличием МГД-волн в солнечном ветре. Поскольку управляющий параметр входит в (4) в комбинации Eq2, то МГД-волны создают мультипликативные флуктуации, которые следует учесть при стохастическом обобщении уравнения (3). Третий вопрос относится к происхождению и спектрально-временной структуре флуктуаций управляющего параметра. Мы ограничимся здесь лишь общими сведениями. Перед фронтом околоземной ударной волны перманентно существуют турбулентные пульсации электромагнитного поля, причем их спектр охватывает диапазон частот от миллигерц до нескольких килогерц [Russell, Hoppe, 1983]. Эти пульсации зарождаются в результате нетривиального взаимодействия ионов и электронов солнечного ветра с ударным фронтом. Волновые возмущения существуют и в свободном солнечном ветре. Они распространяются от Солнца в виде волн Альф-вена, а также зарождаются в межпланетном пространстве между Солнцем и Землей в результате шланговой и других неустойчивостей межпланетной плазмы.
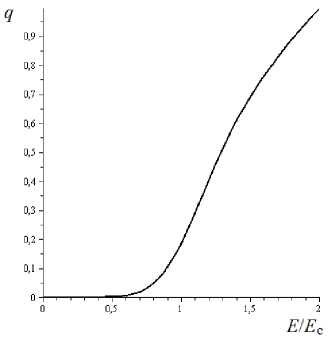
3. ИНТЕГРАЛЬНОЕ ПРЕДСТАВЛЕНИЕ В данном случае задача состоит в том, чтобы найти подходящую форму стохастического обобщения модели RBM. Рассмотрим еще раз рис. 1. Видно, что при динамической трактовке величина q вблизи порога зависит корневым образом от межпланетного электрического поля E. Обратим внимание на интересную аналогию: в ряде случаев сечение ядерной реакции точно так же корневым образом зависит от энергии частицы, налетающей на ядро. Это наблюдение подсказало нам возможность использовать методический прием, предложенный в монографии [Мигдал, 1975]. Допустим вначале, что флуктуаций межпланетного электрического поля нет. Введем интегральное представление функции q(E): q(E)=J§(E-E)VE -Ec dE . (5) Ec Нетрудно увидеть, что это не более чем новое аналитическое выражение для функции, изображенной на рис. 1. Действительно, из (5) следует, что q=0 при E<Ec и q = ^E - Ec при E>Ec, как это и показано на рис. 1. Однако в реальных условиях величина межпланетного электрического поля отнюдь не фиксирована. Она флуктуирует около некоторого среднего значения E. Интегральное представление (5) подсказывает, что следует заменить дельта-функцию на подходящую функцию распределения: да ________________ q(E)=J f (E-E)VE-Ec dE . (6) Ec Если мы выберем распределение Гаусса f ( x ) exp о V2n i Г- T 2 Vo) со среднеквадратичным отклонением s, то из (6) получим О Г ГE-E= YIn ГE= -E) q(E)=\exp -l I D-3/21 I V 2 V 20 ) x о ) где D–3/2 — функция параболического цилиндра. Проанализируем формулу (8). Используем асимптотику функции параболического цилиндра [Градштейн, Рыжик, 1962], положим о=const и найдем, что q=0 при E^-ю и q=E1/2 при E^+«, как и ожидалось по смыслу вывода формулы (8). Если же E=const и о^0, то из (8) следует бифуркационная диаграмма, изображенная на рис. 1. Таким образом, в трех предельных случаях имеется полное соответствие между стохастической и детерминистической моделями RBM. При малых, но конечных о влияние флуктуаций сказывается сильнее всего в небольшой окрестности порога. Рисунок 2 иллюстрирует это положение при о=0.2. Ясно видно, что корневая сингулярность исчезла, т. е. порог сгладился. Кроме того, порог несколько сместился влево.
4. ОБСУЖДЕНИЕ Dst-вариация относится к определенному классу геофизических явлений, отличительное свойство которых состоит в том, что функция состояния системы непрерывна, однако производная функции по управляющему параметру испытывает скачок при переходе через пороговое значение управляющего Рис. 2. Сглаживание и смещение порога под воздействием мультипликативных флуктуаций управляющего параметра параметра. В статистической физике этому соответствуют фазовые переходы второго рода [Ландау, Лифшиц, 2005]. Пороговая сингулярность возникла в связи с идеализацией, а идеализация состояла в том, что в нашей теории, представленной уравнениями (2)–(4), произведена феноменологическая редукция неопределенно большого числа степеней свободы магнитосферы и солнечного ветра. При необходимости неучтенные степени свободы можно включить в теорию в форме аддитивных или мультипликативных шумов. Эта ситуация отнюдь не уникальна. В геофизике известно немало пороговых явлений, родственных фазовым переходам второго рода. Ниже будут приведены несколько типичных примеров. В каждом из них можно учесть флуктуации путем интегрального представления бифуркационной диаграммы подобно тому, как это было сделано нами при стохастическом обобщении RBM-модели Dst-вариации. В качестве хорошо известного примера можно указать на самовозбуждение ионно-циклотронных волн в радиационном поясе Земли. В этом случае удается отыскать в явном виде порог и определить эволюцию системы при переходе через порог, используя фундаментальные уравнения электродинамики плазмы [Guglielmi, Pokhotelov, 1996; Kangas et al., 1998]. Однако многие другие случаи не поддаются последовательному анализу на основе общих принципов. Вместо этого приходится формировать феноменологические модели на основе наблюдений и физических соображений. Типичным примером может служить модель ветровой генерации атмосферного электричества на дрейфующей льдине «Северный полюс – 22» [Гульельми и др., 1979]. Управляющим параметром является скорость ветра. Критическое значение скорости 4 м/с найдено из наблюдений и обосновано общими соображениями об электризации частичек снега и льда в воздушном потоке. Еще один пример относится к движению жидкости в порах и трещинах горных пород. Обычно скорость просачивания жидкости V в пористом теле описывают законом Дарси V=KDI, где KD — коэффициент линейной фильтрации, I — градиент напора [Коллинз, 1964]. Однако опыт показывает, что существуют режимы фильтрации, при которых следует вносить поправки в линейный закон Дарси. В частности, эффективный коэффициент проницаемости K(I, δI) при I=0 равен K (0,51 ) = dV = KD I=0 1 f I 1 I= 1 - erf _ c IV2 51 , где δI — флуктуации градиента напора, Ic — так называемый порог Злочевской [Гульельми, 2002]. Это значит, что коэффициент проницаемости, измеренный в лаборатории на реальном образце горной породы, будет ниже коэффициента Дарси KD. Опыт феноменологического моделирования пороговых явлений свидетельствует о том, что иногда общий облик геофизического процесса подсказывает форму кривой перехода и даже позволяет угадать вид дифференциального уравнения, описывающего процесс, как это было при моделировании Dst-вариации. Удачный выбор уравнения эволюции особенно важен при попытке выйти за рамки класса рассмотренных нами явлений, подобных фазовым переходам второго рода. В ряде случаев простое уравнение демпфированного осциллятора с квадратичной нелинейностью dx/dt+αx=βx2 (10) может оказаться полезной исходной моделью при поиске ответа на вопрос о типе динамической системы, эволюция которой наблюдается в эксперименте. Поясним сказанное на примере самовозбуждения ионно-циклотронных колебаний в радиационном поясе Земли. В этом случае x — интенсивность колебаний, α — управляющий параметр, зависящий от анизотропии протонов радиационного пояса, причем пороговое значение α=0 [Guglielmi, Pokhotelov, 1996]. Тип динамической системы определяется знаком параметра β. Обычно считается, что β<0 [Kangas et al., 1998]. Если это так, то мы имеем автоколебательную систему с мягким самовозбуждением. Состояние системы x непрерывно зависит от α, но производная x по α испытывает скачок в пороговой точке. Другими словами, если β<0, то самовозбуждение ионно-циклотронных колебаний в радиационном поясе следует отнести к тому же классу, что и Dst-вариацию. Заметим, однако, что гипотезу о жестком самовозбуждении, которое возникает при β>0, пока что исключить нельзя. Известны наблюдения, косвенно свидетельствующие о том, что интенсивность колебаний x, а не только производная x по α терпит разрыв в критической точке α=0. Вопрос о режиме самовозбуждения радиационного пояса до конца не исследован и является дискуссионным. Поиск и изучение систем с жестким самовозбуждением в геофизических средах представляют несомненный интерес. Особенно интересен случай взрывной неустойчивости, при которой x→∞ на конечном отрезке времени. Уравнение (10) имитирует взрывную неустойчивость при α>0, β>0 и достаточно больших начальных значениях x0. Пусть для простоты x0>>α/β. Тогда x (t ) = x0 (1 - t / t0 )-1, (11) где t0=(βx0)–1. Величина x стремится к бесконечности при t→t0. Это значит, что если речь идет, например, о твердом теле, то взрывная неустойчивость неизбежно приводит к его разрушению за время t0. Можно предположить, что взрывная неустойчивость возникает спорадически при образовании магистрального разрыва в очаге землетрясения, при пе-ресоединении силовых линий в нейтральном слое геомагнитного хвоста и, по всей видимости, во многих других природных явлениях. Вернемся еще раз к уравнению (10). Отбросим второй член в левой части, положим β=–1 и запишем уравнение в виде dn/dt=–n2. Данное уравнение не представляет никакого интереса с точки зрения физики пороговых явлений. Оно описывает, например, рекомбинацию, приводящую к монотонному понижению числа n пар противоположно заряженных частиц в ионосферной плазме. Однако обратим внимание на интересное обстоятельство. Решение уравнения n~t–1 имитирует эмпирический закон Омори, который описывает монотонное уменьшение с течением времени числа афтершоков после сильного землетрясения [Omori, 1894]. Возможно, это просто совпадение. И все же было бы интересно сделать попытку увидеть смысл в аналогии между динамикой афтершоков и рекомбинацией зарядов противоположного знака в ионосферной плазме. В связи с этим можно сделать следующие замечания. Известно, что квадратичная нелинейность в уравнении рекомбинации возникает вследствие парных соударений при равенстве концентраций положительно и отрицательно заряженных частиц (указанное равенство выполняется в плазме с большой точностью). Если придавать какое-то значение нашей попытке, то не следует ли обратить внимание на отдаленное подобие между парой противоположно заряженных частиц в плазме и парой бортов разлома в земной коре. Если продолжить рассуждение в том же направлении, то нам придется сделать следующий шаг и со всеми необходимыми оговорками провести аналогию между средним временем ожидания столкновения пары зарядов противоположного знака и средним временем активизации пары смежных бортов разлома. На этом пути можно попытаться построить рекомбинационную модель потока афтершоков. Вполне понятно, что эти рассуждения неполны. Они пока что не приблизили нас к более глубокому пониманию физики землетрясений. И не исключено, что мы имеем дело с простым совпадением. В таком случае уравнение dn/dt=–n2 придется рассматривать всего лишь как эквивалентную форму записи эмпирического закона Омори. Однако даже в этом случае появляется дополнительная возможность искать поправки к закону Омори. Например, если в уравнении dn/dt= –n2 учесть диффузионный член, т. е. записать его в виде dn / dt = -n2 + D V2 n, (12) то сразу напрашивается переход к хорошо известному в математике и биологии классическому уравнению ФКПП [Fisher, 1937; Колмогоров и др., 1937]. Используя многообразие решений уравнения ФКПП, мы расширим наши возможности при поиске адекватных моделей пространственно-временного распределения афтершоков. ЗАКЛЮЧЕНИЕ В настоящей работе обсуждались проблемы феноменологического моделирования Dst-вариации геомагнитной бури. Описана модифицированная модель RBM и поставлен вопрос о необходимости стохастического обобщения этой модели. Обращено внимание на формальное сходство между пороговыми особенностями в теории ядерных реакций и в теории Dst-вариации, что дало возможность использовать интегральное представление бифуркационной диаграммы, давно известное в квантовой теории. Это позволило учесть влияние флуктуаций, которые устраняют корневую сингулярность диаграммы и приводят к смещению пороговой точки. По мнению автора, особенно важно, что Dst-вариация принадлежит к широкому классу явлений в магнитосфере, атмосфере и литосфере Земли, родственных фазовым переходам второго рода. Автор благодарит А.С. Потапова за интерес к данной работе и ценные замечания. Работа выполнена в рамках проектов РФФИ 15-05-00491 и 16-05-00056.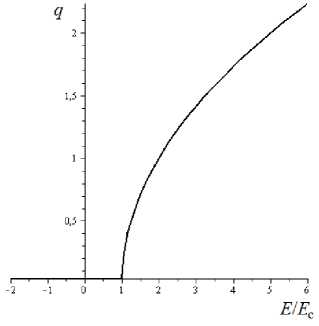
Список литературы О феноменологической теории магнитных бурь
- Гилмор Р. Прикладная теория катастроф. М.: Мир, 1984. 350 с.
- Градштейн И.С., Рыжик И.М. Таблицы интегралов, сумм, рядов и произведений. М.: Государственное издательство физико-математической литературы, 1962. 1100 с.
- Гульельми А.В. Проблемы феноменологического моделирования Dst-вариации//Геомагнетизм и аэрономия. 1988. Т. 28, № 2. С. 272-276.
- Гульельми А.В. О пороговых явлениях в геоэлектрике//Физика Земли. 2002. № 4. С. 75-77.
- Гульельми А.В., Клайн Б.И., Русаков Н.Н. Геоэлектрическое поле по наблюдениям на дрейфующей станции «Северный полюс-22»//Геофизический сборник АН УССР. 1979. Вып. 88. С. 60-64.
- Гульельми А.В., Полюшкина Т.Н., Потапов А.С. Поиск оптимальной формы источника в RBM-модели Dst-вари-ации//Исследования по геомагнетизму, аэрономии и физике Солнца. 1989. Вып. 85. C. 95-100.
- Данжи Дж. Космическая электродинамика. М.: Госатомиздат, 1961. 208 с.
- Колмогоров А.Н., Петровский Н.Г., Пискунов Н.С. Исследование уравнения диффузии, соединенной с возрастанием количества вещества, и его применение к одной биологической проблеме//Бюл. МГУ. Сер. А: Математика и механика. 1937. Т. 1, № 6. С. 1-16.
- Коллинз Р. Течения жидкостей через пористые материалы. М.: Мир, 1964. 352 с.
- Ландау Л.Д., Лифшиц Е.М. Статистическая физика. Часть 1. М.: Физматлит, 2005. 616 с.
- Мигдал А.Б. Качественные методы в квантовой теории поля. М.: Наука, 1975. 336 с.
- Нишида А. Геомагнитный диагноз магнитосферы. М.: Наука, 1980. 299 с.
- Burton R.K., McPherron R.L., Russell C.T. An empirical relationship between interplanetary conditions and Dst//J. Geophys. Res. 1975. V. 80, N 31. P. 4204-4214.
- Fisher R.A. The wave of advance of advantageous genes//Annual Eugenics. 1937. V. 7. P. 355-369.
- Goldstein M.L. Major unsolved problems in space plasma physics//Astrophys. and Space Sci. 2001. V. 277, N 1/2. P. 349-369.
- Guglielmi A.V., Pokhotelov O.A. Geoelectromagnetic Waves. IOP Publ. Ltd.: Bristol and Philadelphia, 1996. 402 p.
- Horsthemke W., Lefever R. Noise-Induced Transitions. Berlin: Springer, 1984. 299 p.
- Kangas J., Guglielmi A., Pokhotelov O. Morphology and physics of short-period magnetic pulsations (A Review)//Space Sci. Rev. 1998. V. 83. P. 435-512.
- Omori F. On after-shocks//Rep. Imp. Earthq. Inv. Corn. 1894. V. 2. P. 103-138.
- Russell C.T., Hoppe M.M. Upstream waves and particles//Space Sci. Rev. 1983. V. 34, N 2. P. 155-172.


