О фильтрации воды и воздуха в почвах и грунтах при защите от подтопления

Фильтрация воды или воздуха в почвах и грунтах количественно может быть рассчитана с помощью закона Дарси. Однако совместное движение воды и воздуха в пористой среде – более сложный процесс, описание которого до сих пор носит дискуссионный характер. Необходимо совершенствовать методологию наших представлений о совместной фильтрации воды и воздуха в почвах и грунтах, отталкиваясь от изначальных теоретических основ с опорой на опытные данные. Попыткой решения этой задачи в первом приближении и является представленная работа.

Объекты и методы

Фильтрацией принято называть движение жидкости или газа в пористой среде. Под средой подразумевают твердую фазу. Общее же название для любой жидкости или газа – флюид [1]. Большинство сред – пористые, трещиноватые или трещиновато-пористые: почвы, грунты, бетон, кирпич и т.д. Движение жидкости или газа происходит по сообщающимся между собой порам или трещинам. Такие среды именуют фильтрующими, или проницаемыми. Это могут быть почвы, грунты (пески, супеси, суглинки), строительные материалы (щебень, гравий, пористый бетон, кирпичная кладка) и т.д.

В теории о защите от подтопления в городском строительстве и сельском хозяйстве рассматриваются закономерности фильтрации воды и воздуха с практической целью проведения количественных расчетов и моделирования по определению:

• –    положения уровня подземных вод (УПВ) при обследовании, строительстве или эксплуатации защищаемых территорий, зданий и сооружений;

• –    водопритоков в мелиоративные каналы, строительные котлованы, траншеи, подземные проходки, системы водопонижения и дренажа;

• –    движения влаги и воздуха в специальных вентиляционных, вакуумных и других защитных системах от подтопления.

Закон Дарси (основной закон фильтрации) для воды связывает скорость фильтрации V (м/сут) с коэффициентом фильтрации пористой среды k (м/сут), разностью напоров (потерями напора) Δ H (м) и длиной пути фильтрации L (м)

V = k Δ H / L .                                   (1)

Для любого флюида (жидкости или газа) закон Дарси связывает скорость фильтрации V (м/сут) с коэффициентом проницаемости пористой среды k 0 (м²), динамической вязкостью флюида μ 0 (Па·с), разностью приведенных давлений (потерями давления) Δ p пр (м) и длиной пути фильтрации L (м) [2]

V = k 0 Δ p пр / ( μ 0 L ).                                       (2)

Приведенное давление для флюидов p пр в гидрогеологии рассмотрел А.И. Силин-Бекчурин [3]. Величина p пр подробно представлена в учебном пособии В.И. Сологаева «Механика жидкости и газа». Для газов в величине p пр обычно не учитывают силу тяжести вследствие малого удельного веса газа γ г [4].

Коэффициент проницаемости k 0 (м²) и фильтрации по воде k (м/сут) связан зависимостями:

k = 86400 γk 0 / μ 0                                       (3)

или k = 86400gk0 / νводы,                                      (4)

где γ – удельный вес воды при температуре 10 ºС, Н/м³; μ 0 – динамическая вязкость воды, Па∙с; g – ускорение свободного падения, м/с²; ν воды – кинематическая вязкость воды, м²/с. Здесь и ниже, если коэффициент фильтрации вычислять стандартно в СИ в м/с, то никакие числовые коэффициенты типа 86400 в формулах не нужны. При температуре 10 ºС можно записать простую переводную формулу для коэффициента фильтрации (м/сут)

k = 6,49 ∙ 10¹¹ k 0 .                                              (5)

В строительных нормах приводят так называемое сопротивление воздухопроницанию Ru , м²∙ч∙Па/кг, которое относят к определенной толщине строительного материала δ , м. Его можно пересчитать на коэффициенты проницаемости k 0 (м²) и фильтрации по воде k (м/сут) с помощью формул:

k 0 = δν возд / (3600 Ru )                                       (6)

и k = gδνвозд / (3600νводыRu),                                   (7)

где ν возд – кинематическая вязкость воздуха, м²/с.

Газы (например, воздух), в отличие от большинства жидкостей, сжимаемы, поэтому для них удобно применять массовую скорость фильтрации

WГ = ρV,(8)

где ρ – плотность газа, кг/м³.

Фильтрационный (объемный) расход несжимаемой жидкости (м3/сут)

Q = V ω,(9)

где ω – площадь живого сечения, м².

Газы сжимаемы, для них применяют массовый расход, кг/сут

GГ = WГ ω = ρωV = ρQ.(10)

Рассмотрим трубу, через которую фильтруется воздух под влиянием разности приведенных давлений Δpпр = p1 – p2 при постоянной температуре T (рис. 1). Труба заполнена материалом с проницаемостью k0; длина пути фильтрации L;     P} ■'' ■                      Ч Pi живое (поперечное) сечение фильтрационного потока ω. Фильтрация газа подчиняется закону        ү LI

Дарси, т.е. происходит в ламинарном режиме.

В условиях давлений, соизмеримых с ат-             Рис. 1. Фильтрация воздуха мосферным pатм, воздух можно считать идеаль ным газом. Поэтому плотность воздуха можно определять по уравнению Д.И. Менделеева и Б.П. Клапейрона (B.P. Clapeyron)

ρ = p / β ,                                              (11)

где β = R г T – константа; R г – газовая постоянная для воздуха, Дж/(кг∙К); T – абсолютная температура воздуха, К.

Так как каждому давлению воздуха соответствует своя плотность, для вычисления его массового расхода по формуле (10) следует взять среднюю величину плотности

ρ = ( ρ 1 + ρ 2 ) / 2 = ( p 1 + p 2 ) / (2 β ).

Тогда массовый расход воздуха по (10) с учетом (2) и формулы Менделеева и Клапейрона (11) можно записать после несложных алгебраических преобразований

G Г = k 0 ω ( p 1 ² + p 2 ²) / (2 μ 0 β L ) .                                (12)

Если требуется вычислить не массовый, а объемный расход воздуха Q , его надо привести к нормальному атмосферному давлению p атм = 101325 Па. Это можно сделать следующим образом. Допустим, вычисляем расход, выходящий из правого сечения трубы при давлении воздуха p 2 (рис. 1). По закону Роберта Бойля (R. Boyle) и Эдма Мариотта (A. Mariotte)

p _атм V _атм = p 2 V 2 ,                                          (13)

где V атм и V 2 – объемы воздуха соответственно при атмосферном давлении p атм и при p 2 . Разделим обе части уравнения на время t и выразим объемный расход воздуха, приведенный к атмосферному давлению

Q = Q атм = ( p 2 / p атм ) Q 2 .

Подставим массовый расход по (12), учитывая (10) и (11). Тогда после сокращений получим объемный расход воздуха, приведенный к атмосферному давлению

Q = k 0 ω ( p 1 ² + p 2 ²) / (2 μ 0 p атм L ) .                                (14)

Если через трубу фильтруется вода под влиянием разности напоров Δ H = H 1 – H 2 , объемный расход по закону Дарси для воды (1) с учетом (9) можно записать

Q = k ω ( H 1 + H 2 ) / L.                                 (15)

Сравнивая (14) и (15), нетрудно заметить, что выражения идентичны, если иметь в виду замену k H = k0 p2 / (2 μ0 pатм).                                      (16)

Такая аналогия впервые была замечена Л.С. Лейбензоном [5]. При использовании формул (14) и (15) следует учитывать размерности величин. Указанная аналогия позволяет преобразовывать известные аналитические решения, полученные в теории фильтрации воды, в решения для движения газа (воздуха) в пористой среде. И, наоборот, известные решения из области фильтрации газа – для движения воды в почвах и грунтах.

Рассмотрим теперь другой, более сложный процесс совместной фильтрации воды и воздуха. При насыщении пористой среды частично водой и воздухом они взаимно влияют на проницаемость друг друга. Тогда вводят понятие фазовой проницаемости по жидкости k w (воде) и газу k g (воздуху) с размерностью м² [6]. Можно также называть k w – водопроницаемость, а k g – воздухопроницаемость. Обзор теории фазовой проницаемости изложен в [2]. Рассмотрим фазовую проницаемость песчаных и глинистых грунтов. Для характеристики фазовой проницаемости флюида необходимо ввести понятия влажности и степени влажности грунта.

Влажность грунта W (кг/кг) – это отношение массы воды в объеме грунта к массе этого грунта, высушенного до постоянной массы (массовая влажность). Это стандартный термин по ГОСТ 5180–84 «Грунты. Методы лабораторного определения физических характеристик». Обычно влажность W выражают в %, но допускается и в долях единицы. Иногда W называют влагосодержанием [6].

Объемная влажность w – отношение объема воды в грунте к объему этого грунта, высушенного до постоянной массы [7]. Связаны объемная и массовая влажности формулами:

w = (1 – n )( ρ s / ρ ) W                                    (17)

и w = (ρd / ρ) W,                                         (18)

где n – пористость грунта; ρ – плотность воды, кг/м³; ρ s – плотность частиц грунта, кг/м³; ρ d – плотность сухого грунта, кг/м³ [8].

Для большинства песчаных и глинистых грунтов, анализируя их инженерную петрологию [8], приближенно можно записать w ≈ 2,7 (1 – n) W. (19)

Гигроскопическая влажность W м по ГОСТу – это влажность грунта в воздушно-сухом состоянии, т.е. в состоянии равновесия с влажностью и температурой окружающего воздуха.

Величине массовой влажности W м соответствует объемная гигроскопическая влажность w м , при которой начинается движение воды в порах грунта под влиянием силы тяжести. А.Ф. Лебедев назвал эту величину максимальной молекулярной влагоемкостью [9].

Степень влажности (насыщенности) грунта водой G – это отношение измеренной влажности грунта W (кг/кг) к его влажности в состоянии полного водонасыщения без воздуха W 0 (кг/кг), т.е. [10, 11]

G = W / W 0 .                                    (20)

Диапазон степени влажности грунта

0 ≤ G ≤ 1.

При предельных значениях G фазовая проницаемость по воде или воздуху стремится к коэффициенту проницаемости пористой среды k 0 (м²).

Например, при G = 1 грунт полностью водонасыщен и фазовая проницаемость по воде kw = k0, а по воздуху kg = 0. Воздух не может пройти через грунт, у которого поры полностью заполнены водой. Даже при не совсем полном водонасыщении грунта воздухопроницаемость может быть нулевой.

Фазовая проницаемость по воде была изучена С.Ф. Аверьяновым [12], который теорети-

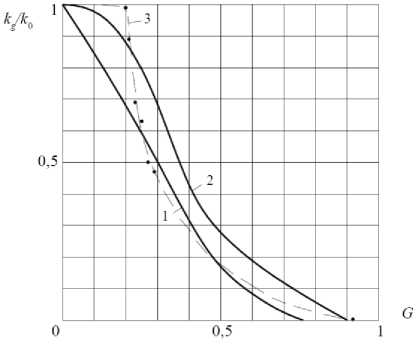
Рис. 2. Зависимость относительной фазовой проницаемости по воздуху:

1 - для глинистых грунтов [6]; 2 - для песчаных грунтов [4, 17]; 3 - опытная кривая автора с точками для неравномерно увлажненного песка

ческим путем получил формулу для коэффициента водопроницаемости грунта, содержащего воздух kw = к [(w - Wм) / (n - Wм)]3,5. (21)

Формула проверена многочисленными лабораторными и полевыми опытами отечественных и зарубежных исследователей [13, 14, 15, 16], она достоверна.

На рис. 2 показаны зависимости относительной воздухопроницаемости k _g / к ₀ от степени влажности G песчаных и глинистых грунтов. Для сравнения точками показаны результаты опытов автора.

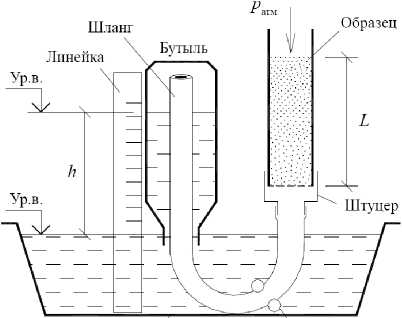
Нами проведены лабораторные опыты по определению воздухопроницаемости песка с разной степенью влажности. Разработан простой, недорогой и достаточно точный прибор (рис. 3), дающий погрешность изме-

рения величин воздухопроницаемости почвы или грунта менее 1 %. Прибор позволяет создавать небольшой вакуум, одновременно измеряя объемный расход воздуха, проходящего через образец пористого материала.

Пробка

Ванночка /              \3ажим

Рис. 3. Прибор для измерения воздухопроницаемости

Для сборки прибора потребовалась стеклянная бутыль с нанесенной шкалой объемов, резиновый шланг с внешним диаметром меньше внутреннего диаметра горлышка бутыли (с зазором), стеклянная трубка, заполненная песком с мелкой сеткой внизу, пробка и штуцер, зажим для шланга, широкая ванночка, резиновая груша. Бутыль и трубку с образцом пористого материала подвешивают на штатив. «Ур. в.» означает «уровень воды».

Перепад приведенных давлений при фильтрации воздуха через пористый образец создается вакуумом рв = үһ, где ү - удельный вес воды; h - разность уровней воды в бутыли и ванночке. Вначале сухой шланг заводят в бутыль до ее дна. Бутыль переворачивают и подвешивают на штатив так, чтобы горлышко погрузилось под уровень воды в ван- ночке на 1 см. Воздух из бутыли отсасывается через шланг резиновой грушей, пока уровень воды в бутыли не поднимется до перевернутого дна бутыли, но так, чтобы не перелиться через шланг (вода не должна попадать в шланг). Шланг перекрывается зажимом, присоединяется через штуцер к трубке с образцом пористого материала (почвы или грунта), на которую сверху надета герметичная пробка (рис. 3). Все соединения промазывают пластичным герметиком. Прибор готов к проведению опыта.

При одновременном открытии зажима и пробки воздух стремится пройти через пористый образец в бутыль. При этом уровень воды в бутыли постепенно падает. Данный процесс с уче- том закона Дарси для газа (2) можно описать исходным дифференциальным уравнением баланса воздуха

ω Б ( dh / dt ) = ω k g γ h / ( μ 0 L ), (22)

где ω Б – площадь внутреннего поперечного сечения бутыли; t – время; ω – поперечное сечение образца; L – путь фильтрации (рис. 3); k g – коэффициент воздухопроницаемости образца при определенной степени влажности; μ 0 – динамическая вязкость воздуха при определенной температуре; γ – удельный вес воды. Так как средний вакуум был около 0,1 м вод. ст. (1 % от р атм ), изменение объемов воздуха по закону Бойля и Мариотта (13) не учитывалось вследствие малой погрешности.

При начальном перепаде уровней воды h0 (начальное условие) записанное исходное уравнение имеет решение, выраженное относительно коэффициента воздухопроницаемости k0 = [μ0 ωБ L ln(h0/h)] / (ω γ t). (23)

Формула использована для обработки опытных данных. Она аналогична известной формуле для прибора-трубки Г.Н. Каменского [18], предназначенной для определения коэффициента фильтрации песков.

В качестве образца пористого материала был взят чистый речной песок с эффективным диаметром d 10 = 0,1 мм и коэффициентом неоднородности K н = 2. Коэффициент фильтрации песка по воде k = 9,98 м/сут, его среднее значение определено на приборе Тима [7] из серии опытов. В высушенном состоянии на нашем приборе (рис. 3) определен коэффициент проницаемости песка k 0 = 1,53 ∙ 10^–11 м², это соответствует k = 9,93 м/сут. Таким образом, проницаемости по воде и воздуху практически совпали.

В начале опытов песок находился в воздушно-сухом состоянии толщиной L = 10 см. Его воздухопроницаемость k g практически равнялась проницаемости k 0 , о чем свидетельствует самая высокая опытная точка на графике (рис. 2). Затем на поверхности песка была проведена инфильтрация воды в виде капель. Верхний слой песка около 1 см потемнел. Его проницаемость резко упала – примерно в 630 раз при степени влажности песка около G = 0,92. Лишь через 2 сут произошел некий «прорыв»: на рис. 2 соответствует опытной точке при G = 0,3. Это можно объяснить рассасыванием воды равномерно по толщине песка (цвет стал равномерным по всей толщине). Величина G для большей надежности опыта определена двумя независимыми способами: по объему воды в каплях и при взвешивании образца с трубкой на лабораторных весах. Таким образом, получены опытные точки, показанные на рис. 2.

По результатам этих опытов можно сделать интересный вывод, затрагивающий вопросы вакуумного водопонижения с учетом прорыва воздуха в скважины. Пористый материал (грунт) становится практически непроницаемым не от равномерной влажности, а от слоистой. Таким образом, в дождливый период не следует ожидать прорывов воздуха в иглофильтры и вакуумные скважины.

Закл ючение

В представленной работе предпринято дополнительное исследование совместного движения воды и воздуха в почвах и грунтах. Начальные теоретические выкладки с фундаментальными законами Дарси, Бойля, Мариотта, Менделеева, Клапейрона позволили обратить внимание будущих исследователей – продолжателей данной темы – на аналогию движения воды и воздуха в пористой среде. Это позволит преобразовывать известные аналитические решения, полученные в теории фильтрации воды, в решения для движения газа (воздуха) в пористой среде. И, наоборот, известные решения из области фильтрации газа – в решения для движения воды в почвах и грунтах. Проделанный автором дополнительный лабораторный эксперимент по фильтрации воздуха через образец грунта дал дополнительную для размышления информацию: о влиянии слоистого увлажнения среды на движение воздуха. Автор надеется на продолжение теоретических и экспериментальных исследований по затронутой теме о закономерностях совместной фильтрации воды и воздуха в почвах и грунтах при защите от подтопления в городском строительстве и сельском хозяйстве.