О фокусировке цилиндрически симметричной ударной волны в газе

Математическое моделирование динамических процессов в механике сплошных сред в настоящее время является одним из важнейших инструментов исследований. Для решения конкретных задач используются уже существующие или создаются новые модели и численные методы. Для оценки свойств разностных схем, аппроксимирующих законы сохранения, широко применяются априорные методы, такие, как исследование устойчивости, аппроксимации, консервативности, дистракции и др. Следует, однако, отметить, что большая часть этих методов разработана для акустических приближений к исходным уравнениям и для простейших уравнений состояния. В механике сплошных сред свойства математической модели из-за нелинейностей, определяемых реальными уравнениями состояния, наличием ударных волн, пластичностью и другими свойствами вещества, могут заметно отличаться от предсказаний линейной теории.

При переходе к нелинейным уравнениям линейная теория теряет свою строгость. Важность теоремы сходимости [1] сильно преувеличивается, поскольку она все-таки доказана для линейных, а не для нелинейных уравнений, а реальные расчеты проводятся при конечных Ax и At, а не при Ax ^ 0, At ^ 0. Очень ярко взгляды на относительность «строгих» критериев устойчивости и сходимости изложены в [2]. Поэтому важнейшими способом проверки достоинств и недостатков математической модели в настоящее время является расчет эталонных задач, имеющих аналитическое решение, и сравнение результатов расчетов с этими решениями. Начиная с 40-х годов прошлого столетия появился ряд работ [3-11], содержащих автомодельное решение задачи о фокусировке ударной волны в бесконечном идеальном газе. Однако реальные тела имеют конечные размеры. В данной работе рассмотрена задача о сходящейся ударной волне в цилиндрическом сосуде с непроницаемой стенкой, имеющая аналитическое решение.

1.    Постановка задачи

Рассматривается цилиндрический сосуд с непроницаемой стенкой, в котором находится газ массой M0 и начальными при t = t о параметрами газа р о = const, U0 = 0, P 0 = 0, Е о = 0, г де р - плотность, U - скорость, P - давление, Е - удельная внутренняя энергия. Задача имеет цилиндрическую симметрию. Лагранжевой координатой является цилиндрическая масса M. Второй независимой переменной является время t. В точке t о, M0 задана скорость U 1 <  0. Таким образом, в этой точке задан сильный разрыв, который при t > t о распространяется к центру симметрии и в момент t f фокусируется в точку M = 0. Граница цилиндра при t > t о движется в переменных r, t, но в переменных M, t ее траектория является вертикальной линией. Вообще говоря, все траектории частиц являются вертикальными линиями, вдоль которых сохраняется то значение энтропии, которое возникло на ударной волне. Параметры газа между ударной волной и границей определяются системой законов сохранения Эйлера-Гельмгольца. Уравнение состояния используются в двух формах

P = ( y - 1) рЕ,    P = F ( s ) Р⁷,                        (1)

где F ( s ) - функция от энтропии.

2.    Соотношения на ударной волне

Законы сохранения на ударной волне при U _о = 0 , P о = 0 , Е о = 0 , F о = 0 имеют вид [12]

P w ( D ^— U w ) ^— Р о D = ^{0 ,}                            ( 2 )

р о DU w - P w = 0 ,

^р о D ^E w + ^ Uw)

- P w U w = 0 .

Индексом «w» обозначены величины на ударной волне, D - скорость ударной волны. Преобразуем эти уравнения к виду, содержащему зависимости U_w, р_w, F_w, P w от скорости ударной волны в лагранжевых координатах. Лагранжева координата M w ударной волны в случае сферически симметричного течения связана с ее эйлеровой координатой r w уравнением

M w = пр о r w . (5)

Скорость ударной волны в лагранжевых координатах есть изменение Mw со временем dMw

W = —= 2 пр о r w D. dt

Заменим эйлерову координату ударной волны ее лагранжевой координатой. Для этого выразим r w из (5) и подставим в (6)

W = (2Mw)1/2 (2про)1/2 D.(7)

Выразив в (7) D через W и M w и подставив в (2)-(4), получим с помощью (1) зависимости

Y + 1 рw

Y - ¹

Uw = ^+1 (2 пр о) -1/2 (3 Mw) -1/2 W,(9)

Pw = Y+1 (2 п)-1 (2 Mw)-1 W2.(10)

Из (1), (8) и (10) следует выражение для F w

Fw =       ()—1) y р- (2п)-О (2Mw)-1 W2.(11)

В точке t = t о- M w = M 0. U w = U w 0. P w = P w 0- F w = F w 0.

U w = U 0 ( W И M T - P w = P0 ( W ⁾² ( MT ) ■ F w = F о ( W ⁾² ( M ) .

W 0 M w            W 0 M w           W 0 M w

По аналогии с [13-14] зададим траекторию ударной волны в виде

M w = M 0 ф ( t ) n ,                               (13)

где ф = ( t f — t ) / ( t f — 1 ₀). Продифферейдировав M_w по t , получим выражение для скорости ударной волны в лагранжевых координатах

W = W 0 ф^{п- 1} ,                               (14)

где	W 0 = — T M 0^ .                           (15) t f — t 0

Исключив в (13) и (14) функцию от времени, получим зависимость W от M_w

W _ ( M w )( n - 1)/ n W 0    (m эУ       .

С помощью соотношения (16) исключим W в (12)

U w = U w 0	Mw\ ( n - 2)/2 n                Mw\ ( n - 2)/ n               MMW\ ( n - 2)/2 n (M о)       ,  Pw = Pw 0 ( m о)       ,  Fw = Fw 0 ( m э)       .
48	Bulletin of the South Ural State University. Ser. Mathematical Modelling, Programming & Computer Software (Bulletin SUSU MMCS), 2017, vol. 10, no. 4, pp. 46-55

Величина F w вдоль траектории частицы с координатой M w постоянна. Следовательно, зависимость энтропии от массы между ударной волной и границей газа имеет вид

/ М \ ⁽ n - ^2)/ n

^F - F w 0 Ы

.

Из (5) следует зависимость r w от M w

_  ⁽ M w ^)1/2

r w    r ⁰ \М э)

.

• 3.    Параметры течения за фронтом ударной волны Параметры адиабатического течения за ударной волной определяются уравнениями, траектории, сохранения массы и движения

(dr) м - U-о -

( дР ) м -пр2 U-0,01.

(IU) +2.7 -0.(22)

∂t M ∂M

Эти уравнения содержат три искомых функции г, р и U. Величина F определяется на ударной волне и зависит только от M (17).

Перейдем в (20) - (22) к новым искомым функциям

R = r ² ,

C = rU.

После перехода к функциям R и C уравнения (20) - (22) примут вид

( R — 2 ° -0 -∂t _M

∂ρ         ∂C

(at) м ^{+ 2 np}dM ^-0

дС 1 ,      д ( Fp ' )

( at )_м ^{+ R} эм

- 2 C ² R

¹ - 0 .

Из (17), (19) и (23) следуют зависимости R w и C w от M w

R = R Mw  c   M,-  . n- 1)/ n

.

R w   ^{R 0} M э ’ C w   C ⁰ M о

Уравнения (24) - (26) являются основными для отыскания R, C и р в области интегрирования M w < M < M ₀. 1 0 < t < tf.

Перейдем от переменных t, M к переменным t, ф ( t, M ). Уравнения (24) - (26) примут вид

(+               - 2 C = 0 ,

∂t ξ ∂ξ t ∂t M

^{( dp} ) + ⁽ ?£ ) ⁽ 21 ) +2 np 2 ⁽ ^ ) ⁽ ^2 ) =0 , ∂t _ξ ∂ξ _t ∂t _M          ∂ξ _t ∂M _t

(9. ам -

C ²

R +

+2-V®.®?'"

∂ρ ∂ξ

∂ξ t ∂M t

= 0 .

Зависимость ф ( t, M ) зададим так. чтобы ii а ударной волне было ф = следует, что проще всего взять такую зависимость в виде

M -n ф   Mо Ф '

1. Из (13)

4. Разделение переменных

Представим R, p и C в виде произведений двух функций, одна из которых является функцией только t, а другая только от ф

R = a R ( t ) T ( ф ) p = a p ( t ) 5 ( ф )    C = a c ( t ) Z ( ф ) .

Поскольку на ударной волне ф = 1, то значения T 1 = T (1) , 5 ₁ = 5 (1) , Z ₁ = Z (1) должны быть постоянными. Из (27) и (31) следует зависимость R w ( t )

R w = R о ф ^п .

Сравнив эту зависимость с (32) на ударной волне, получим выражение для a R a R ( t ) = R о ф^п T- ¹ .

Аналогично для ap и ac получаем соотношения ap = Ро (^—1) 5-1,   ac (t) = Cо фп-1 Z-1.

Подставив (32) - (35) в (28) - (30) и воспользовавшись (15), получим три уравнения для T. 5 II Z

фТ ‘ = A 1 ,

-

δ 1 B 1 Z^′

4-z' + Z 1

-

^Z 1 8 = 0 ,

C-^ 5- = C 2 , δ 1

где штрих означает дифференцирование по ф . Коэффициенты уравнений (36) - (38)

A 1 , B 1 , C 1 , C 2 с помощью (5). (6). (12)

A -T   ² ZT ¹    R

A ¹ = ^{T -} (у+ДД ^{, B 1}

_C =    z ² t 1

²   ( ' +1) z 2 T

и (21) преобразуются к виду

-

2 5 ²

⁽ Y - 1) ⁵ 12 ’ ( n - 1) Z

C 1 =

_δ γ - 1 _{T ξ}- 2/ n

^δ 1 ^γ

n Z 1

-

⁽ n - ^{2) 5}

^{C 1}   n δ 1

1 _{T 1}

.

Уравнения (36) - (38) образуют относительно T', 6, Z' систему линейных неоднородных уравнений. Определитель системы равен

А = B i C i y( - ( ² .

Если А = 0,

то решение системы

′ ^A 1

( ’

(36) - (38) существует и имеет вид

′    B 1 C 2 δ 1      ′    ξC 2 Z 1

А ,        А

.

На ударной значения

волне при

( = 1

величины Т, 6 , Z, А и коэффициенты (39) принимают

T = T 1 ,

6 = 6 1 ,

(д — 1) Т-i

Z = Z I , A 1 = ^{( Y} J ¹ ,

Y + 1

C 1 = 1 ,

C 2 =

3 ( y + 1) - n (2 Y + 1)

n ( Y + 1)

, А(1)

о _   2

B 1 — 7-----7

⁽ Y ^- 1)

= ⁽ Y + 1)

⁽ Y ^- 1) '

5.    Решение

Интегрирование системы уравнений (40) начинается в точке ( = 1 (на ударной волне). Расчеты показывают, что существует промежуток значений n таких, что определитель в ноль не обращается. При некотором значении n* определитель обращается в ноль при ( = (* . В этой точке решение существует, если C2 тоже обращается в ноль. Каждому значению y соответствует одно значение n* (см. табл.). В этой же таблице приведены значение (* , при которых одновременно А ( (* ) = 0, C2 ( (* ) = 0 . Профили давлений, плотностей и скоростей при n = n* для трех моментов времени приведены на рис. 1.

Таблица

Значения n* 11 (* . соответствующие различным зиачеииям показателя адиабаты y

γ	1,1	1,2	4/3	1,4	5/3
n∗	1,770501	1,722331	1,684516	1,670651	1,631252
ξ∗	6,768540	4,873946	3,896265	3,616019	2,990161

При 0 < n < n* определитель системы уравнений (40) положителен во всем промежутке изменения ( 1 < ( < то . В этом случае происходит коллапс газового цилиндра - его объем стремится к нулю. Структура течения газа между фронтом ударной волны и границей цилиндра показана на рис. 2.

В области n > n* определитель обращается в iюль при некотором значении (п. которое зависит от n. Но в этой точке C2 ((п) в ноль не обращается. Таким образом решение существует в области 1 < ( < (п. На границе газов ого цилиндра при M = M0 значение (п достигается в момент tn = tf - (tf - tо) ^п 1/n.

Из точки M о , t n выходит лшшя. на, которой ( = (_п

M n = M о ( n f ^ -t.

t f - t 0

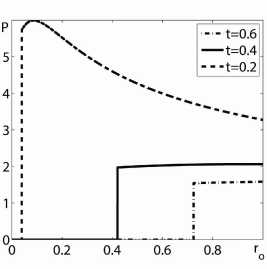
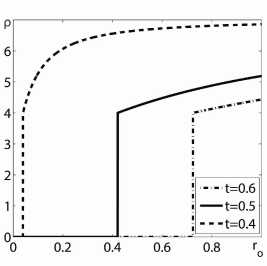
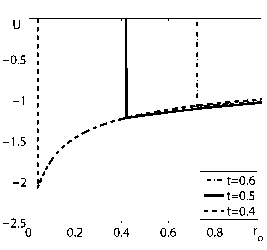
Рис. 1. Зависимости скорости, давления и плотности от эйлеровой координаты r для 7 =5/3, n = n* = 1 , 631252 и трех моментов времени

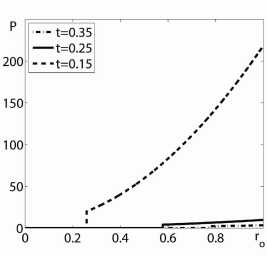
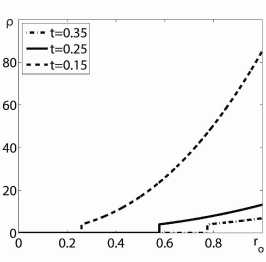
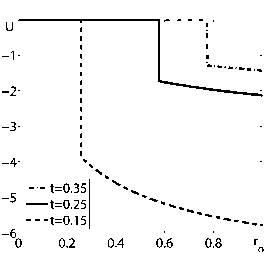
Рис. 2. Зависимости скорости, давления и плотности от лагранжевой координаты для Y =5/3, n = 1 мен вше n* =1 , 631252 и трех моментов времени

Она фокусируется одновременно с ударной волной, т.к. при t = tf, M_n = 0. В области между линией (41) и ударной волной (13) для каждого n > n* существует единственное решение. Структура течения газа показана на рис. 3.

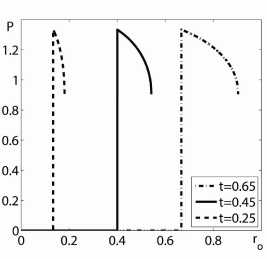
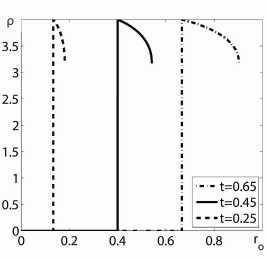
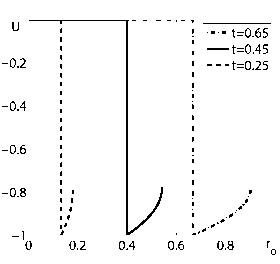
Рис. 3. Зависимости скорости, давления и плотности от эйлеровой координаты r между ударной волной и характеристикой для y=5/3, n = 2 больше n*=1, 631252 и трех моментов времени

В лагранжевых координатах построено аналитическое решение задачи о цилиндрически симметричной сходящейся ударной волне для произвольных показателей n, которые определяют схождение ударной волны.

Статья выполнена при поддержке Правительства РФ (Постановление № 211 от 16.03.2013 г.), соглашение № 02.АО3.21.ООП.