О формировании предельных распределений вероятности равновесных состояний нелинейных динамических систем со случайными параметрами

При изучении динамических, эволюционных процессов, связанных с формированием равновесных состояний сложных систем, одной из важных задач представляется определение вероятностных характеристик таких состояний (в дальнейшем мы называем их «предельные состояния»). Причиной неопределенностей здесь являются как недетерминированность параметров самой системы, так и неопределенности в задании начальных условий. Сложные систе-

ВЕСТНИК 2016

мы, как правило, имеют не одно, а несколько состояний равновесия (в том числе и несколько устойчивых состояний равновесия, проявляя свойство мультистабильности); и вероятности формирования предельных состояний довольно сложным образом связаны с характеристиками тех случайных величин, характеристики которых можно считать априорно известными.

Задачи подобного характера возникают в исследовании мультистабильности нелинейных систем [1-3], в исследовании динамики многокомпонентных спектров при волновой диагностике нестационарных диспергирующих сред [4-6], в моделировании социальных явлений [7; 8] и т.п.

Рассматриваемый в настоящей работе подход к анализу формирования статистических распределений характеристик предельных состояний основывается на расчете геометрической вероятности, определяемой по пространственной структуре сепаратрисных множеств и, соответственно, по вариациям реализующихся решений обыкновенных дифференциальных уравнений (ОДУ) относительно границ, определенных этими множествами. Такие вариации, в свою очередь, обусловлены случайными изменениями начальных условий и/или вариациями самих границ, связанными со случайными параметрами самой системы. Функции распределения ве- роятности этих характеристик мы считаем ста- ционарными.

Конкретика применения данного алгоритма существенно зависит от структуры сепаратрис-ных множеств, поэтому мы будем иллюстрировать его особенности на конкретном примере -задаче о «конкуренции». Применение данного подхода для иных ОДУ, описывающих нелинейную динамическую систему, в целом имеет ту же последовательность операций, но каждый шаг будет иметь специфику, определяемую спецификой задачи.

• II.    Сепаратрисные множества для системы нелинейных ОДУ

Рассмотрим систему нелинейных ОДУ типа уравнений Вольтерра для конкурентных взаимодействий [9], в которую добавлены члены третьего порядка:

dx                  2

— = а_ху - a₂xy - a₃x у dt ^{1       2        3}

1 , dy

— = b 1 x - b ₂ xy - b ₃ xy

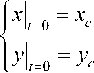
Согласно [8], такая система может описывать конкуренцию бизнесов, с учетом ограничений законодательного порядка. Условно назовем их бизнес Х и бизнес Y . Для дальнейшего рассмотрения конкретика модели определяет только особенности геометрии рассматриваемых далее множеств, но не меняет структуры алгоритма исследования. Поэтому для иллюстрации мы не только будем пользоваться примером (1), (2), но и применять некоторые смысловые представления данного примера. Так, величины x ( t ) и y ( t ) мы рассматриваем как отклонение от устоявшегося в среднем баланса объемов производств соответственно первого и второго бизнесов. Коэффициенты at и b - действительные положительные величины, характеризующие в соответствующих компонентах правой части уравнений (1) соответственно: взаимную адаптацию (договоренность) бизнесов ( г = 1), их конкуренцию ( г = 2) и ограничения, возникающие при различных нарушениях законодательства ( t = 3) [8].

Уравнения (1) позволяют легко определить координаты критических точек, точек равновесия:

X о = 0, Y = 0;

X 1,2 =

12 ± а 22 + 4 а1 а 3

2 0 3          ^;

- b ₂ ± 7 b ₂ ² + 4 b 1 b₃

Верхний знак «+» соответствует индексу «1», нижний «-» - индексу «2». Анализ этих точек показывает, что точка ( Х ₀, Y ₀) является седловой точкой, а остальные - критические точки - представляют собой узлы, причем точки ( Х 1 , Y 1 ) и ( Х , , Y , ) - это устойчивые узлы, а точки ( Х 1 , Y 2 ) и ( Х , , Y 1 ) - неустойчивые узлы. При выполнении условий Y 1 ₂ * 7 а ₂ ² + 4 а 1 а ₃ = X ₁₂ * 7 b ₂ ² + 4 b 1 b ₃

соответствующие узлы - вырожденные. В данной модели устойчивые узлы мы и рассматриваем как конечные предельные состояния данной системы при t ^+ ^ .

Семейство решений системы (1) задается первым интегралом:

| у - Y Y (| x - X ,1 X J где параметр д определен формулой:

ц = ^b22 + 4b1 b3 = b3 *(Y1 - Y2)

7 а ₂ ² + 4 а 1 а ₃    ^а 3 *⁽ X 1 ^- X 2 )

Траектории системы (1) лежат на линиях уровня функции (5) F (x , y ) = F(x c , y_c ) = C , причем уровень C = 0 определяет две прямые y = Y 1 , y = Y 2 , а уровень C = да - прямые x = X 1 , x = X ₂.

«Особым решением», представляющим интерес для дальнейшего, является линия уровня

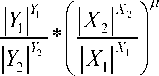
= const ,

проходящая во втором и четвёртом квадрантах и соединяющая точки ( Х ₁, Y ₂), ( Х ₂, Y ₁) и ( Х ₀, Y ₀). Она является сепаратрисой седловой точки ( Х ₀, Y ₀).

Общая геометрическая структура множества решений системы (1) приведена на рисунке 1. Для примера выбраны следующие значения параметров: a₁ = 0,6, a ₂ = 0,4, a 3 = 0,25 и b 1 = 0,3, b ₂ = 0,27, b ₃ = 0,375.

Из представленного анализа и рисунка 1 сле-

дует, что координатная плоскость пространства решений разделена на четыре области:

• 1)    S 1 - область, ограниченная линией { x = X ₂ , y >  Y } , особым решением и линией { x >  X 1 , y = Y 2 } ; в этой области все решения стягиваются к устойчивому узлу ( X 1 , Y 1 ) ;

• 2)    S ₂ – область, ограниченная линией { x ≤ X ₂, y = Y 1 } , особым решением и линией { x = X 1 , y <  Y ₂ } ; в этой области все решения стягиваются к устойчивому узлу ( X ₂ , Y 2 ) ;

• 3)    S 3 = { x <  X 2 , y >  Y } и S 4 = { x >  X 1 , y <  Y 2 } -области, в которых решения при t ^ + да не ограничены, траектории уходят на бесконечность.

Границы перечисленных областей мы называем сепаратрисным множеством, поскольку они разделяют качественно различные предельные значения решений { x ( t ) , y ( t ) } при t ^ + да . На рисунке 1 и далее это множество изображено жирными линиями.

Интерпретируя в терминах взаимодействия бизнесов полученные результаты для системы (1), можно сказать, что стабилизация уровней производства как бизнеса X , так и бизнеса Y происходит в зонах S ₁ и S ₂ вне зависимости от начальных условий (2), причем предельное состояние системы в каждой из указанных зон – единственное. Напротив, в зонах S ₃ и S ₄ не существует стабильных состояний «сосуществования» бизнесов: в зоне S ₃ в конкурентной борьбе побеждает бизнес Y , а в зоне S 4 – бизнес X , то есть возникает монополия. Понятно, что случай чрезмерно больших производств монопольного бизнеса не описывается данной системой уравнений, так как модель всегда имеет ограниченную область применимости.

III. Динамические нелинейные системы ОДУ со случайными параметрами

В данном разделе рассмотрим, как изменятся характеристики предельных состояний в случае, когда параметры системы (1) случайные.

1. Пусть случайной величиной является начальное состояние системы, начальные условия (2). Предположим, что координаты точки ( x_c , y_c ) есть нормально распределенная двумерная случайная величина, заданная следующей функцией плотности распределения вероятности:

xcyc

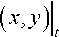
1*

2по_хо ₂

*exp

( x - а ) ² 2 о -1²

( у - Р )² )

ВЕСТНИК 2016

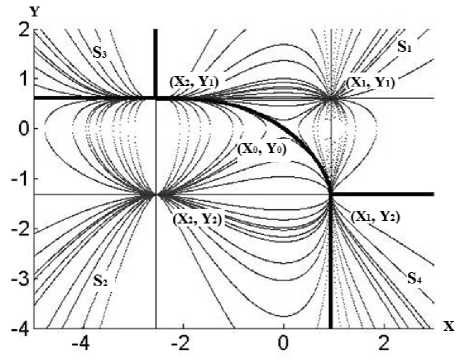
Рис. 1. Геометрия множества решений системы (1)

Понятно, что если математическое ожидание координат M ( x_c , y_c ) = ( а , в ) находится далеко от сепаратрисного множества, то предельное состояние с вероятностью, близкой к 1, совпадает с точкой ( X 2 , Y 2 ) , если ( а , Р ) е S ₂ , и с точкой ( X 1 , Y 1 ) , если ( а , Р ) е S 1 . То есть:

Р х ( t ) . ( t ) ( ^Х , У )| t _„ ^

^ ( x - X₂, y - Y 2 ) при ( а, p ) G S ₂, ⁽⁸⁾ 5 ( x - X i , y - Y ) при ( а , в ) g S j .

С вероятностью, близкой к единице, стабильного сосуществования двух бизнесов не будет, если ( а , p ) е S ₃ ^ S ₄ .

«Близость» начальных условий к сепара-трисному множеству можно оценить 3 σ -окрест-ностью, которую можно задать, например, следующим условием:

{| х_с - а | <  3^ 1 , Уу_с - в <  3 ^ 2 } •              ⁽⁹⁾

ВЕСТНИК 2016

Тогда если начальные условия, удовлетворяющие (9), одновременно удовлетворяют и условию ( x_c , y c ) e S 2 , то с вероятностью 0,9973 реализуется предельное состояние ( X 2 , Y 2 ), если же выполнено условие ( x c , y c ) е S 1 , то реализуется предельное состояние ( X 1 , Y 1 ).

В общей ситуации для рассматриваемого случая вероятности предельных состояний задаются формулами:

P = P ( x ( t , x c , y_c )| t , = X ₂,

• У ⁽ t , x c , У с )| t .. = Y 2 ) =                     (10)

• = JJ P xy. ⁽ x , У )| t = 0 dxdy ’

• ⁵ 2

• ^P 1 = P ( x ( t , x c , У с )| t = X_p

• y ⁽ t , x c , У с )l t ,., = ^ =                     ⁽ⁱⁱ⁾

• = If P xy. ( x , У )| t = 0 dxdy■

S 1

Вероятность отсутствия конечных предельных состояний, очевидно, равна:

P.   1 - P i - P 2 .                         (12)

Соответственно, предельная плотность распределения вероятности будет такова:

P x ( t ) y ( t ) ⁽ x , У )| t ,, ^—

—>^P 2 * 5 ( x — X 2 , y — Y 2 ) +

• + P * 5 ( x — X 1 , y — Y i ) .

Вычисления вероятностей предельных состояний по формулам (10), (11) и (12) иллюстрируют графики зависимости этих величин от положения центра функции плотности распределения вероятности координаты точки (6) (рис. 2 (2а, 2б, 2в)).

Расчеты проведены для распределения (7) при <71 = < r ₂ = 0,5 .

Данные зависимости полностью соответствуют качественным результатам, представлен- ным выше.

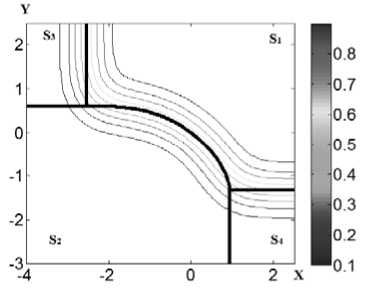
Рис. 2а. Вероятность P ₁ (графики линий уровней) для бимодальной системы в зависимости от положения центра распределения координат начальной точки

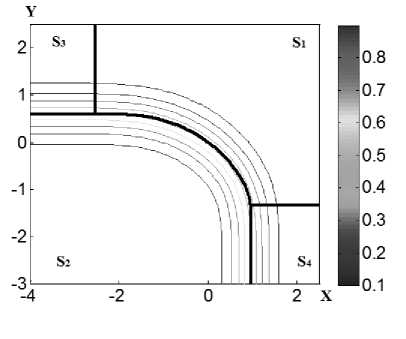
Рис. 2б. Вероятность P ₂ (графики линий уровней) для бимодальной системы в зависимости от положения центра распределения координат начальной точки

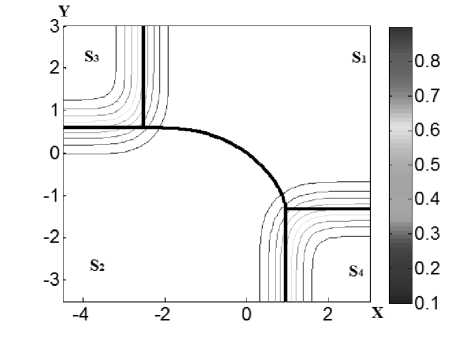
Рис. 2в. Вероятность P „ (графики линий уровней) для бимодальной системы в зависимости от положения центра распределения координат начальной точки

Поскольку выражения (10)–(12) задают вероятности попадания точки ( x , y ) в соответствующие зоны при t ^+ ^ , мы фактически получаем условные вероятности предельных состояний системы при заданной начальной точке ( x , y ) = = ( x c , У с ) .

В частности, P 1 | _{Х с} = _{х 2}, _Л = Y 2 = P ( x ( t , X ₂, Y 2 )| _t ^₊„ = = X ,, y ( t , X. , Y. )|    = Y ) представляет услов-

• ^{1         22} t ^+^   ¹

ную вероятность возникновения предельного состояния ( X i , Y ) при заданном (в среднем) начальном состоянии ( X ₂ , Y 2 ) . Соответственно, ^P 2| x c = _х 1 , y c = Y 1 = ^P ( ^x ( t , X 1 , Y D| t ^₊„ = X₂, y ( t , X j , Y ) | t ^_+m = Y ₂) есть условная вероятность возникновения предельного состояния ( X ₂, Y , ) при заданном начальном состоянии ( Х ₁, Y ₁). Например, для модельных расчетов, соответствующих рис. 2, P _{1 x = Xy = Y} ≈ 0.00006 , P             ≈ 0.02.                   ^{c 2 , y c 2}

• ² x _c = X ₁, y _c = Y ₁

Аналогичным образом, через характеристики (10)–(12) определяется вероятность таких процессов, как реализация и нереали-зация предельного состояния ( X ₁, Y ₁) при заданном (в среднем) начальном состоянии ( X ₁, Y 1 ): соответственно P x = x_y = P ⁽ x ⁽ t , X_p Y ) t , = = ^X i , У ( t , ^X i , Y )| . .+„ = Y ) ‘ "и       ¹ - P x c = X , y c = y =

= 1 -P(x(t,X1,Y)|t       X1, y(t,X1,Y)|t       Y); реа лизация и нереализация предельного состояния (X2, Y2) при заданном (в среднем) начальном состоянии (X2, Y2): Px = x2,yc=y2 = P(x(t,X2,Y)|t= = X2, y (t, X2, Y2 )| = Y2) и 1 - P          =

• ^{2                2}’ ² t ^+^ ^{2                           2} x, = Хз , y_ = Y-,

c 2 c 2

= 1 - P (x (t, X2, Y2>|,= X2, У (t, X2, ^2>| ,    = Y^ , и других аналогичных характеристик. Для иллюстративного примера это соответственно вероятности: P »0,98, 1- P        ~ 0,02,

• ¹    I x c - X 1 , y_c ^- Y                           ^lx c - X 1 , y c - Y

  P I _{Y Y} » 0,99994, 1 - P I          » 0,00006.

• ²    x c ^- X 2 , У с ^- Y 2                           ² x c ^- X 2 , У с ^- Y 2

• 2.    Рассмотрим теперь ситуацию, когда случайными характеристиками являются коэффициенты уравнений системы (1). В этом случае возникает неопределенность как в положениях самих точек равновесия (3), так и в положении сепаратрисного множества.

Положим для простоты, что параметры системы (1) a ₁ и b ₁ – непрерывные случайные независимые величины, плотность распределения вероятности которых задана Г-распределением 2-го порядка (такая модель обеспечивает условие положительности данных величин), а параметры a ₂, a ₃ и b ₂, b ₃ – детерминированные величины. Начальная точка ( x_c , y_c ) траектории системы (1) также детерминированная величина. Таким образом, имеем случайные параметры a ₁ и b ₁, заданные распределениями с плотностями вида:

X a ² 1 * exp ( -X a t ) , при t >  0

0,                при t <  0’

X b ² 1 * exp ( -X b t ) , при t >  0

0,                при t <  0

Пусть уравнение области S_i в координатах ( x , y ) имеет вид:

5 , = { Ф ' ( x , y ) >  0 } , j = 1,2,....             (15)

Тогда вероятность попадания точки (x, y) в область Si определяется, как геометрическая ве- роятность, выражением:

P - P ( (x, y) G ^. ) - P и ф' (x, y) > 0 к j

^ф j ^{( x} , У ) есть детерминированные функции случайных величин a ₁ и b ₁ и при фиксированных координатах точки ( x , y ) задают отображение области S_i (15) в область S _i в пространстве ( a ₁, b ₁). Следовательно, равенство (16) представимо в виде:

Pi - P ( (x, У)G Si ) - JJ Pa, ( t )* Pb1 ( Г ) dtdT, (17) S, где двумерная плотность распределения вероятности определена из (14).

В рассматриваемой модели для областей S ₃ и S ₄ формула (17) принимает вид:

jj Pai()* PbY (Т)dtdT +

—

a ₂

—-

aa

— x > 0

y

+

2 a ₃

• ^{— b} 2 ⁺ 7 ^b 22 ^{+ 4 b}1^b 3 > 0

_{2 b 3}

jj Pa, (t)* Pb, (t)dtdT-

— a 2 +"^ a 2 + 4 a , a 3

x --> 0

2 a ₃

— b 2 — д/ b 22 + 4 b i b 3

2 b ₃

— y > 0

Для областей S ₁ и S ₂ уравнение для элемента границы, представленного особым решением (6), не разрешается в явном виде. Потому формулы (16) и (17) существенно не упрощаются.

Как и в случае п. 1 , выражения (16)–(18) задают вероятности попадания точки ( x , y ) в соответствующие зоны, разделенные сепаратрисным множеством (хотя в данном случае оно является случайным), и мы опять получаем условные вероятности предельных состояний системы при заданной начальной точке ( x , y ) = ( x_c , y_c ). При этом, в зонах S ₁ и S ₂ координаты положений равновесия также являются случайными величинами с условными средними значениями (при заданной начальной точке траектории):

• X , - JJ P a , ( t ) • P b (T ) - a ² ± ^^{22 + 4} ta 3 «Г, (19)

S i                             2 a 3

^Y i ^- JJ Pa, ( t ) * P b , ( ^T ) ^{b 2} "^ ^b 2 ^{+ 4} — ^{dtd T} , ⁽²⁰⁾

S i                           ^{2 b} 3

i = 1, 2 соответственно для областей устойчивого состояния S , и S ₂, знак « ± » определен в (3). Отметим, что зависимость значений интегралов (19) и (20) от ( x_c , y_c ) возникает только из-за зависимости от этих параметров самой геометрии области интегрирования S_i (см., например, явные зависимости в формуле (18)).

ВЕСТНИК 2016

ВЕСТНИК 2016

Очевидно обобщение выражений (17)–(20) на случай многомерных распределений случайных параметров a_j и b_j j = 1,2,3 системы (1). Следует най_~ти лишь отображение области S_i (15) в область S _i в пространстве всех параметров a_j и b_j j = 1, 2, 3 и записать формулу (17) для 6-мерного пространства параметров, задав функцию плотности совместного распределения вероятности для этих элементов.

Расчеты вероятностей P ₁, P ₂ , P _∞ по формулам (17), (18) при заданной функции плотности распределения вероятности параметров (14) качественно повторяют результаты расчетов п. 1.

Заключение

Таким образом, проведенное исследование модели формирования предельных состояний двухкомпонентной динамической системы на основе расчета геометрической вероятности реализации различных областей в пространстве переменных ( x , y ), границы которых задаются сепаратрисным множеством, показывает эффективность такого подхода. Данный метод можно применить для решения задач формирования состояний квантовых систем, исследования распространения волн в средах со случайными неоднородностями, исследования динамических систем различной природы. Определенный интерес представляет возможность использования данного подхода в исследовании эффектов типа «подбарьерного просачивания» и «надбарьерного отражения».

Хотя в данной работе фактор неопределенности в коэффициентах системы (1) и неопределенность в начальных данных (2) рассмотрены отдельно, при известных функциях совместного распределения вероятности этих величин объединение формул (10), (11) и (17) очевидно.