О формуле Д.С. Львова для оценки машин

Один из методов стоимостной оценки машин и оборудования основывается на формуле Д.С. Львова (в [1, 2] и других учебниках этот метод именуется методом равноэффективного аналога). Приведем ее вывод применительно к ситуации, когда использование машин и оборудования (далее – машины) рассматривается в непрерывном времени, а инфляция отсутствует.

Рассмотрим машину, производящую некоторый продукт (им может быть работа или технологическая операция), имеющую срок службы (полезного использования) T , производительность W и требующую эксплуатационных затрат (без амортизации, но с учетом рыночной арендной платы за занимаемые машиной площади) Z в единицу времени. Пусть p – стоимость единицы продукта. В таком случае в единицу времени машина принесет владельцу (доналоговый) чистый доход D = pW – Z .

При применении сравнительного подхода к оценке активов нередко используются разного рода мультипликаторы, например валовой рентный мультипликатор (отношение стоимости актива к валовому доходу) или мультипликатор EBITDA. Для нашей цели удобнее будет использовать мультипликатор чистого дохода (МЧД) – отношение стоимости объекта к приносимому им доналоговому чистому доходу в единицу времени. Этот показатель, мы будем обозначать его буквой m , близок по величине и экономическому содержанию к мультипликатору EBITDA, а обратной к нему величиной является коэффициент капитализации.

В соответствии с теорией стоимостной оценки стоимость машины V равна сумме дисконтированных ¹ (по доналоговой ставке r ) чистых доходов (см. [3]). Если для упрощения пренебречь утилизационной стоимостью машины, то это равенство примет вид:

^{T                         - rT}

V = J De - rt dt = D 1 e   = ( pW - Z ) m ( T,r ) ,                                             (1)

0r где m(T, r) – МЧД, зависимость которого от срока службы машины и ставки дисконтирования выражается формулой:

T                  — rT m (T;r ) = Je" rtdt = 1 e .                                                                    (2)

₀ r

Обычно стоимость p производимого продукта оценщикам неизвестна (например, потому что этот продукт непосредственно на рынке не обращается). Тогда оценить стоимость машины по формуле (1) нельзя. Но для этого можно использовать данные о стоимости машины-аналога, производящей тот же продукт. Напишем равенство (1) для этого аналога, отмечая его характеристики нижним индексом «a»:

V a = ( PW a - Z a ) ™ ( Т а ,Г ) •

Отсюда находим выражение для стоимости единицы продукта:

V^ + Za

Р = ——

W a

.

Подставив это выражение в формулу (1), получим:

W  m ( T,r )

V = V х X--7---7

^a WmT,r aa ,

W

+ Z_a--Z m(T,rY I ^a                           ,

W a

Эта формула (применительно к дискретному времени и в несколько иной форме) была в свое время получена Д.С. Львовым (см. [4]) и длительное время использовалась в СССР для оценки эффективности новой техники и установления цен на новую промышленную продукцию, а в настоящее время рекомендуется в оценочной литературе (например в [1, 2]) для стоимостной оценки машин. Можно показать (см., например, [5, 6]), что она будет верна и в условиях инфляции, если при этом использовать реальную (скорректированную с учетом инфляции), а не номинальную ставку дисконтирования. Также обратим внимание на то, что ставка r – непрерывная , связанная с годовой ставкой ( Y ) соотношением: r = ln(1 + Y ).

В ряде учебников, например в пособии [7], утверждается, что при использовании формулы Львова достаточно принимать в расчет только те статьи затрат («изменяющиеся»), которые у оцениваемой машины и ее аналога различаются. Это – грубая ошибка! На самом деле такие затраты учитывать необходимо. А вот затраты, которые у обеих машин одинаковы в расчете на единицу продукта («условно-переменные»), действительно можно не учитывать. Это становится очевидным, если заметить, что зависящее от затрат второе слагаемое в формуле (5) можно представить в виде WI Za - Z | m (T,r). Поэтому при ис-a ключении указанных затрат оба члена в квадратных скобках уменьшаются одинаково, а их разность не изменяется.

Теперь обратим внимание на то, что ни в самой формуле Львова, ни в приведенной ее модификации (5) стоимость производимого машиной продукта не фигурирует. Это позволяет применять ее и тогда, когда эта стоимость неизвестна, и даже тогда, когда производимый машиной продукт на рынке отсутствует. Главное здесь в том, что производимый машиной продукт нужен участникам рынка, что он обладает определенной полезностью , а, значит, и стоимостью. Более того, формула (4) позволяет эту стоимость ( p ) рассчитать. Нетрудно убедиться, что она оказывается равной отношению совокупных дисконтированных затрат на производство продукта за весь срок службы аналога к дисконтированному объему выпуска этого продукта. Иными словами, стоимость единицы производимого продукта будет равна удельным дисконтированным затратам на производство этого продукта с помощью машины-аналога (см. [8, раздел 10.4.2]). Такой способ определения стоимости продукта полностью соответствует требованиям затратного подхода к оценке.

Однако у приведенной формулы есть существенный недостаток. Дело в том, что машин, не меняющих своих технико-экономических показателей на протяжении срока службы, просто не существует. В противном случае их можно было бы эффективно использовать в течение неограниченного времени. Обычно же с увеличением возраста происходит физическое изнашивание машины, ее производительность снижается, а эксплуатационные затраты увеличиваются. Отметим также, что равенства (1) и (3) справедливы, только если машины используются наиболее эффективно. Но это означает, что и срок их службы выбран так, чтобы сумма дисконтированных чистых доходов от ее использования оказалась наибольшей. В оценочной литературе такой срок именуют экономическим. Отсюда (да и из определения сроков полезного использования в Международных стандартах оценки [3] и в бухгалтерском учете) следует, что по истечении срока службы приносимые машиной чистые доходы становятся отрицательными. В таком случае можно считать, что величина этих чистых доходов с возрастом убывает и в конце срока службы обращается в нуль.

Для многих видов машин с увеличением возраста эксплуатационные затраты увеличиваются все более быстрыми темпами, а производительность прогрессивно снижается (некоторые данные такого рода приведены в работах [5, 9]). В то же время есть оборудование, технико-экономические характеристики которого с возрастом снижаются все более медленно, приближаясь к некоторому предельному уровню. Разумеется, оценщики не имеют достаточно подробной информации о том, как зависят от возраста производительность и эксплуатационные затраты каждого конкретного вида машин или оборудования. Однако изложенные соображения позволяют с определенной долей условности разделить все виды машин на три группы в зависимости от того, каков характер ухудшения техникоэкономических характеристик машины с возрастом.

В первую группу отнесем машины, у которых с возрастом производительность снижается, а эксплуатационные затраты растут все более быстрыми темпами. У таких машин приносимые ими в единицу времени доходы снижаются прогрессивно.

Во вторую группу отнесем машины, у которых с возрастом производительность снижается, а эксплуатационные затраты растут равномерно. У таких машин приносимые ими в единицу времени доходы снижаются также равномерно.

В третью группу отнесем машины, у которых с возрастом производительность снижается, а эксплуатационные затраты растут все медленнее. У таких машин приносимые ими в единицу времени доходы также снижаются все медленнее.

Динамику изменения с возрастом приносимых машинами доходов удобно описывать, введя коэффициент снижения доходов k , зависящий от относительного возраста τ = t / T – отношения возраста машины к сроку ее службы. Представляется, что описать многообразие таких зависимостей можно с помощью предложенного в работах [5, 8] параметрического семейства функций типа:

k T,q ) =

e ^q - e ^{q T} e ^q -1 ^.

В пределе при q → 0 формула (6) принимает особенно простой вид: k ( τ ,0) = 1 – τ , поэтому здесь приносимые машиной чистые доходы будут пропорциональны оставшемуся сроку ее службы.

Можно считать, что значения q в диапазоне от -1,5 до 1,5 отвечают машинам второй группы, q > 1,5 – машинам первой группы, q < -1,5 – машинам третьей группы. На рисунке 1 представлены зависимости (6) для разных значений q .

Для того чтобы учесть физическое изнашивание машин с возрастом, условимся, что входящие в формулу Львова значения производительности ( W ) и эксплуатационных за-

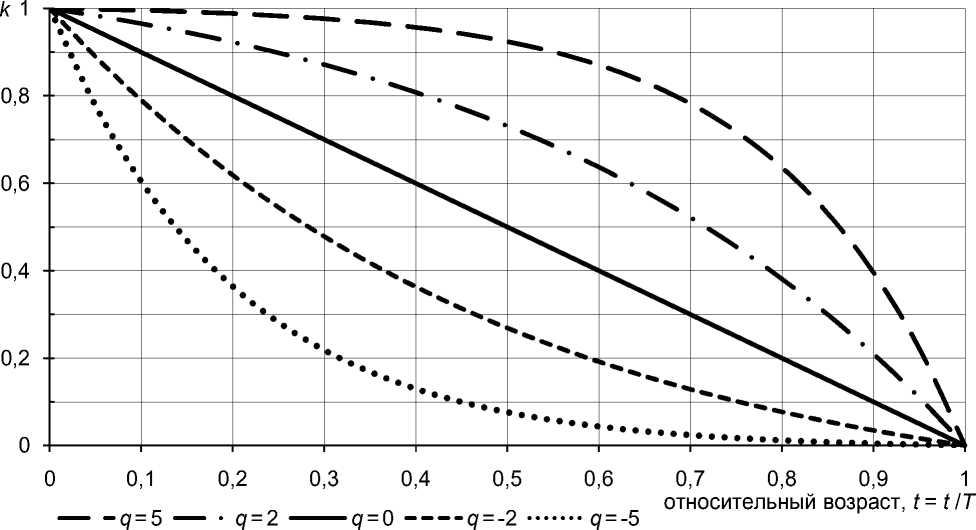
Рис. 1. Зависимости от возраста коэффициентов снижения чистых доходов, приносимых машинами при разных значениях q

трат ( Z ) относятся только к машине в новом состоянии. Это означает, что в начале эксплуатации машина приносит в единицу времени чистый доход D = pW – Z . Однако чистый доход, приносимый в единицу времени такой же машиной возраста t лет, будет отличаться от D понижающим коэффициентом k ( t / T , q ). А тогда формула (1) примет вид:

TT

V = J Dk ( t/T ,q ) e" rt dt = D J k ( t/T ,q ) e" rt dt = ( pW - Z ) m ( t,q,r ) , 00

где m ( t , q,r ) – МЧД, определяемый по формуле:

m ( T,q,r ) =

T e ^q — e qrr

^J e ^q -1

e - rt dt

e ^q -1

e ^q

1 - e ^{- rT}    e ^{q - rT} -1 )

r qT - r)

При q → 0 эта формула упрощается:

m ( T, 0 ,r ) =

rT -1 + e"^rT r 2 T

Как видим, формула (7) отличается от формулы (1) только выражением для МЧД, учитывающего срок службы машины. Это значит, что с учетом физического изнашивания в формуле (5) необходимо только заменить выражения для МЧД. Тогда она примет вид:

.. ..   W   m (T,q,r) ( W)

m ( T,q,r ) .

V = V, x — x —7----v + Z=Z

a Wa m (Ta,q,r) I aWaJ aaa

Кстати, формула (2) получается из формулы (8) предельным переходом при q ^ ^, поэтому и сама формула Львова является предельным частным случаем общей формулы (10).

Представляется, что при отсутствии необходимой информации для машин 1-й, 2-й, 3-й

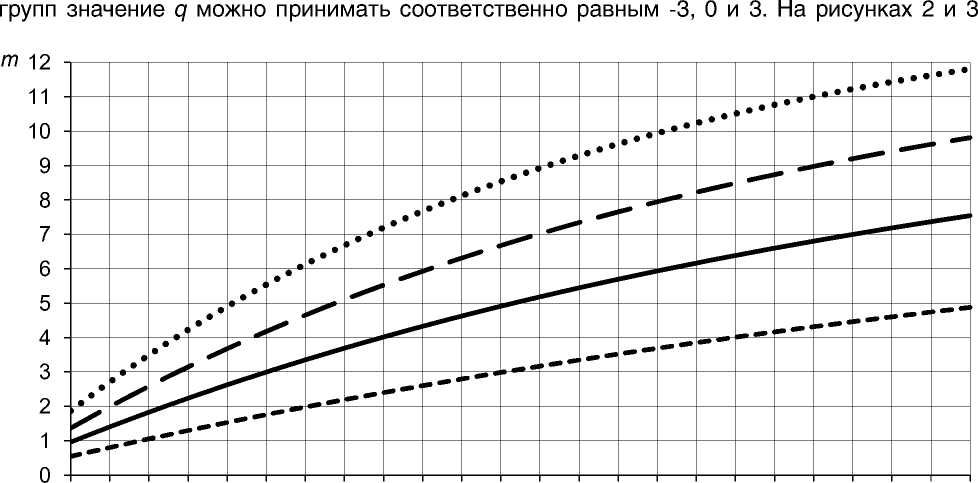
2345678910111213141516171819202122232425 срок службы, годы группа 1   ^^^^^^^^^ группа 2   ^^^^™ ^™ группа 3          Л*

Рис. 2. Зависимости коэффициентов капитализации от сроков службы ( T ) машин разных групп при ставке дисконтирования r = 0,07

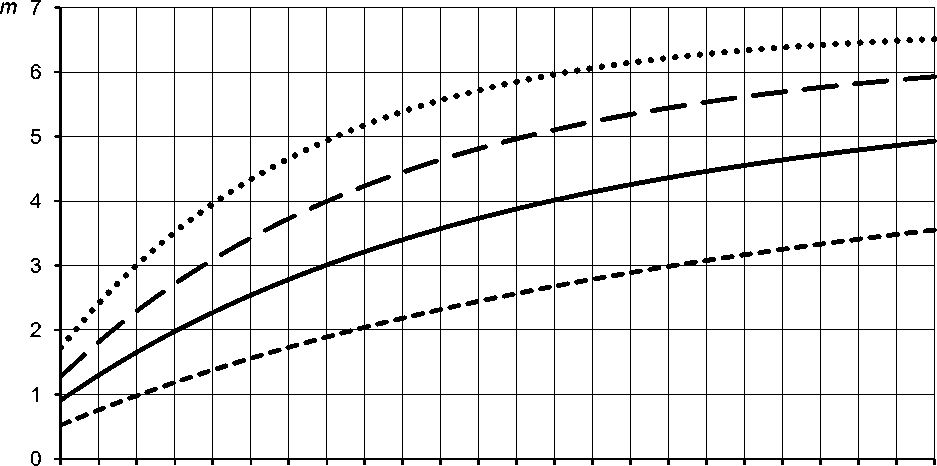
2  3 4  5 6  7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25

срок службы, годы группа 1   ^^^^^^^^™ группа 2   ^^^^™ ^е группа 3          Л

Рис. 3. Зависимости коэффициентов капитализации от сроков службы ( T ) машин разных групп при ставке дисконтирования r = 0,15

Кривой Л представлена зависимость (2) для коэффициента капитализации, отвечающего исходной формуле Львова.

представлены зависимости коэффициентов капитализации для разных сроков службы машины и разных ставок дисконтирования (напомним, что в этом случае эти ставки должны быть доналоговыми, непрерывными, а не годовыми, и реальными, а не номинальными).

Полученные зависимости позволяют более точно учесть особенности физического изнашивания машин. Приведем пример.

Пусть годовая производительность оцениваемой машины W = 250 тысяч деталей, эксплуатационные затраты Z = 200 тысяч рублей, срок службы T = 8 лет. У ее аналога: стоимость V_a = 300 тысяч рублей, W_a = 260 тысяч деталей, Z_a = 218 тысяч рублей, T_a = 7 лет.

Доналоговую непрерывную реальную ставку дисконтирования примем равной 0,1. Используя формулу (2), получим значения коэффициентов капитализации обеих машин: m (8;0,1) = 5,507, m (7;0,1) = 5,034.

При этом стоимость машины окажется меньше стоимости аналога:

V = 300 х ²⁶⁰ х ^{5 , 507} + [200 x ²⁶⁰ - 218^1 x 5 , 507 = 286 .

250 5 , 034 (     250     >

Однако такой расчет не учитывает физическое изнашивание машины. Попробуем его учесть, считая, что машина отнесена во вторую группу. Тогда по формуле (9) находим: m (8;0;0,1) = 3,117, m (7;0;0,1) = 2,808. При этом стоимость машины оказывается больше стоимости аналога:

V = 300 x ²⁶⁰ x ^{2 , 157} + [200 x ²⁶⁰ - 218^ x 3 , 117 = 315.

250 2 , 808 (     250     >

До сих пор процесс использования машины предполагался детерминированным. Между тем машины могут выходить из строя в результате случайных аварий. Оказывается, это можно учесть в формуле Львова. Обозначим через λ интенсивность аварий, то есть вероятность возникновения аварии в единицу времени, и будем считать, что она не зависит от возраста машины ². В таком случае вероятность того, что за время t авария не произойдет, будет равна P ( t ) = e ^{- λ t} . Теперь стоимость машины будет определяться как сумма ожидаемых дисконтированных приносимых ею доходов, для чего доход, приносимый машиной возраста t , надо умножить на вероятность того, что машина доживет до этого возраста, то есть на P ( t ). В результате формулу (7) придется скорректировать так:

V = J Dk ( t(T ,q ) P ( t ) e" rt dt = D j k ( t/T, q ) e - r ^+x) t dt = ( pW - Z ) m ( t, q, r + X ) . 00

Другими словами, для учета возможности аварийного выхода машины из строя мы по-прежнему можем использовать формулу Львова или ее модификацию (10), увеличив при этом ставку дисконтирования на интенсивность аварий.

Выясним, как изменятся результаты приведенного примера, если считать, что интенсивность аварий обеих машин составляет 0,08 (одна авария в среднем за 12,5 года). Скорректированная с учетом риска аварий ставка дисконтирования при этом будет равна 0,1 + 0,08 = 0,18.

Оценим стоимость машины по формуле Львова (5). В этом случае m (8;0,18) = 4,239, m (7;0,18) = 3,980, и тогда:

960 4      (     960A

V = 300 x -6° x - , -39 + l200 x -6° - 218 x 4 , 239 = 290.

250 3, 980 I      250

Если же использовать формулы (10) и (9), то здесь m (8;0;0,18) = 2,612, m (7;0;0,18) = 2,397, а решение окажется иным:

960 9 619 (     960A

V = 300 x -60 x - , 6— + l 200 x -60 - 218 x 2 , 612 = 314.

250 2,397 I      250      )

Как видим, учет риска аварий повлиял на оценку стоимости машины незначительно. При этом, как и без учета риска, модифицированная формула Львова дает более высокую оценку стоимости машины.

Мы выяснили, таким образом, что в первоначальном (обычно приводимом в оценочной литературе) виде формула Львова дает заниженные оценки стоимости машин. Предложенный способ позволяет обобщить эту формулу для учета физического изнашивания машин и риска аварий. Этот способ может быть использован и в тех случаях, когда физическое изнашивание машины и процесс ее отказов описываются другими моделями.