О фундаментальном решении бигармонического уравнения с дельта-функцией в правой части

Рассматривается фундаментальное решение бигармонического уравнения с дельта-функцией в правой части. Это решение важно для получения обобщенного решения бигармонического уравнения с правой частью, зависящей от граничных условий.

On the fundamental solution of the biharmonical equation with the delta-function in the right-hand side

The fundamental solution of the biharmonical equation with the delta-function in the right-hand side is considered. This solution is important for obtaining the generalized solution biharmonical equation with the delta-function in the right-hand side depended from egde conditions.

Бигармоническое уравнение с дельтафункцией в правой части приходится рассматривать при исследовании колебаний механической системы - тела, прикрепленного с помощью упругого элемента к упругой пластине с закрепленными краями [1]. Данная механическая система лежит в основе виброзащитной системы, где тело называется объектом защиты, пластина - основанием, а упругий элемент - виброизолятором. Запишем бигармоническое уравнение с дельта-функцией в правой части в виде:

-й)²Р(х,у) + dV²V²K(x,y) - 5(х)5(у) , (1) где ty - частота, d - некоторая положительная постоянная , V²V²- бигармояиче-ский оператор, 5(х)и ^(у)-дельта- функции.

Фундаментальное решение уравнения (I) будем находить с помощью прямого преобразования Фурье этого уравнения, выделением выражения для прямого преобразования неизвестного решения, а затем применением операции обратного преобра-

зования Фурье к полученному выражению, получение искомого решения.

Установим предварительно некоторые результаты.

Рассмотрим несобственный интеграл

о *2

-а2

cos(Z>Vx sin f)dx

х2 - а2

(2) dt.

где

а и

b - постоянные, J_Q

Бесселя нулевого порядка [2], мая в виде

- функция представи-

1 *

ЛМ) = — Jcos(feVxsinf)t/i.

Вычислим несобственный интеграл ^cos^s/x sin f)dx j x²-a²

Для этого вычислим несобственный ин

теграл

1 Работа выполнена при финансовой поддержке РФФИ (проект 05-01-00659).

С. Г. Баргуев, А.Д. Мижидон. О фундаментальном решении бигармонического уравнения с дельта-функцией в правой части

воспользовавшись тем, .         ехр(Дф z smt'A функция ----- z -а ловиям леммы Жордана

что комплексная

удовлетворяет ус-

Jti(bja)-— fcos(bja sin/)d? -

[3] в верхней по-

луплоскости комплексной плоскости и совпадает с подынтегральной функцией в (4) на действительной оси. Согласно [3] имеем

”rexp(/6V^sin/)tZv _

2 2 х -а

= lim----Г"1---<х " °) + х-я х -а

+ lim

~--г—(х + а) = х -а

= 7ti lim

expfz^Vxsin/)^ _ п              _

-о х-а J exp(i6Vasin/) exp(-£V«sin/)'1

2«            2«

. cost b-Ja sin t) + is\n(b«Ja sin t) Я1--

2л

. expt-b-Ja sin f)

—Я1-------------— la

sin/ - и

= cos tdt - du             =

, du du dt =         =

Vl-sin2/ Vl-w2

_2_ ^} r

^o J\-u²

Продифференцировав предыдущее венство по параметру b-Ja , получим

2b4a 'rsinib-JauAdu ,      ,

=---- |---— = -J/Vbday

О Vl-u2

Отсюда

'fsin(h>/au)zZM я ,,, о -и

Далее, используя (5) и (6), получаем

*\ti^dx = 5 x*-a

■cos(bVxsinf)dx x2 - a2

pa-

dt =

= —— sin(Z>Va sin/) + i—(cos(bVa sin/)~ 2a             2a

-exp(-6Vosin/)).

Далее, учитывая, что

^cosC^Vxsin/)^ _ 1 “r cos(bVa sin t)dx _

J 7^    2 2 x¹-a²   ”

1_ [exp(ih-J"as'mf)dx

Получаем crCOs(Z>Vxsin/Wt я . r- . .

------:----t-² --=--Sin(6Vti Sin/) . (5)

J x -a 4a

Преобразуем J₀(by/a):

1 T

--|sin(h\/a sin/)z// =

4a J

-TU 0

= - — j*sin(6 Ja sin t)dt = 2a ₀

sin / = w cos idt = du

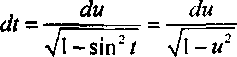
_ 1 'rsm^b-Jau^du _

2a J Vl-»2

2albJ^         4ab4^

Таким образом, о x -a" 4abda

Найдем фундаментальное решение дифференциального уравнения в частных производных вида

-/у²F(x, у) + d^² V² Т(х,у) - 8^5^ • Для этого запишем преобразование Фурье данного уравнения:

-^F(V(x,y)) +

+^(V²V² Г(х,у)) = F(S(x)6(y)).

Обозначим V(x,y) = f. Тогда

F(W*f) = F -L охх

2л jexp(-/1 х [ pcos#*)^ ^2^/0(| х j p^,

Л(1 ^xl P)^{= —} jcos([ x| /?sin^)^

Продолжая вычисление двумерного теграла (9), получим где

ин-

+ 2Д

Эх^дх^

= Н^ Г ?1Л + 2Н£ )² И^ )² Л Л + +№ )⁴ Л Л = £⁴ ЛЛ + 2£²£ ЛЛ+ <ЛЛ-(^+^)²ЛЛ, Г№)Лу))=т

Подставляя в (8), получаем (-я² + d(^ + £ )² )Г [/] = 1. Отсюда

ЛЛ =

-^+^+^)2'

По определению /^"[ЛЛ^ 1

(2л-)2

я.

^-d^Sf

^d£r

Для простоты фиксированный вектор х - (х_р х₂)направим вдоль полярной оси. Тогда угол между вектором £ = (£_р£₂)и вектором х = (х_рх₂) будет равен <р и ехр(-/(х, ^ + х₂^₂)) = ехр(-/| х j | £ | cos ^). Перейдя к полярным координатам, получим

/ = НЛЛ1 =

₌ 1 r rexp(-/|xK|cos^) ₌ (²^)" R, -й,²₊^|⁴

5, =pcow £ = psin?>

№Р

I )_dp_p3y\pp^_dp, ^‘„у  -a'^dp*

(2л-)² J -да² + dp⁴

р

(2л)2 ' -да2 + dp4

1 7 Р

2л -да2 + dp4

p2-t 2pdp = dt

P = 4i

х

f г* _                А j ехр(-/1 х | р cos

1лЗ^\х\р^р =

3^x\p)dp =

1 W\x\4"t) 4л ⁷ -co² + dt²

i U(|x|V7) 4Kd t² - a²

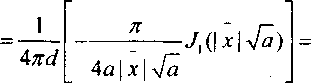
J\(\x\4a) 1 6da | x | Va

т                г Л(\^х\^^аУ

Таким образом, / = ———■——, где 16tfa|x|7a а =    ,      | х |= ^х2 +х2 - ^х2 + у2 или yd

У(х,у) = -^Е^^51. Здесь JQ(y) и \6da^(x +у )а dt(y) - функции Бесселя нулевого и первого порядка некоторого аргумента у соответственно.