О генерации случайных задач линейного программирования на кластерных вычислительных системах

Эпоха больших данных [1, 2] породила задачи линейного программирования (ЛП) сверхбольших размерностей [3]. Подобные задачи возникают в экономике, индустрии, логистике, статистике, квантовой физике и других областях. Решение таких сверхбольших задач невозможно без масштабируемых параллельных алгоритмов, ориентированных на кластерные вычислительные системы. В соответствии с этим в последние годы интенсифицировались усилия по разработке новых и модернизации известных параллельных алгоритмов решения задач ЛП. В качестве примеров можно привести работы [4–8]. При разработке новых масштабируемых алгоритмов для решения сверхбольших задач линейного программирования возникает необходимость их тестирования на известных и случайных задачах. Одним из наиболее известных репозиториев больших задач линейного программирования является Netlib-Lp [9]. Данный репозиторий считается эталонным при апробации новых алгоритмов решения задач линейного программирования. Однако при

^∗ Статья рекомендована к публикации программным комитетом Международной научной конференции «Параллельные вычислительные технологии (ПаВТ) 2021»

отладке решателей часто возникает необходимость в генерации случайных задач ЛП с определенными характеристиками, из которых основными являются размерность пространства и количество ограничений. В работе [10] был предложен один из первых методов генерации случайных задач ЛП с известными решениями. Метод позволяет генерировать тестовые задачи произвольного размера с широким диапазоном числовых характеристик. Идея метода заключается в том, что за основу берется задача ЛП с известным решением, которая затем модифицируется случайным образом так, чтобы решение не изменилось. Основным недостатком этого метода является то, что предварительная фиксация оптимального решения в значительной мере ограничивает случайный характер итоговой задачи ЛП. В [11] предложен генератор GENGUB, позволяющий строить случайные задачи ЛП с известным решением и заданными характеристиками, такими как размер задачи, плотность ненулевых значений матрицы коэффициентов, степень вырожденности, количество неизбыточных неравенств и др. Отличительной особенностью генератора GENGUB является введение обобщенных верхних границ , представляющих собой совокупность ограничений, в которых каждая переменная появляется как минимум один раз (имеет ненулевой коэффициент). Указанный метод имеет тот же недостаток, что и предыдущий: предварительная фиксация оптимального решения в значительной мере ограничивает случайный характер результирующей задачи ЛП. В статье [12] предложен метод генерации случайных задач ЛП с заранее выбранным типом решения: ограниченное или неограниченное, единственное или множественное. В зависимости от выбранного типа решения конструируется допустимая область задачи ЛП как объединение линейного многообразия, конуса и многогранника. Каждая из перечисленных структур генерируется с помощью случайных векторов с целочисленными координатами. Далее генерируется целевая функция, приводящая к решению требуемого типа. Описанный генератор задач ЛП используется в основном для учебных целей и мало подходит для тестирования новых алгоритмов линейного программирования в силу ограниченности многообразия генерируемых задач.

В данной статье предлагается альтернативный способ генерации случайных задач ЛП, особенность которого состоит в том, что генерируются совместные задачи заданной размерности с неизвестным решением. Такая задача подается на вход решателя. Полученное решение проверяется программой-валидатором [13], которая сертифицирует решение. Предложенный метод генерации случайных задач ЛП реализован в виде параллельной программы FRaGenLP ( Feasible Random Generator of LP ) для кластерных вычислительных систем. Статья организована следующим образом. В разделе 1 дается формальное описание предлагаемого метода генерации случайных задач ЛП и приводится последовательная версия алгоритма FRaGenLP. В разделе 2 рассматривается параллельная версия алгоритма FRaGenLP. В разделе 3 предлагается ее реализация с использованием параллельного BSF-каркаса и приводятся результаты масштабных вычислительных экспериментов на кластерной вычислительной системе, подтверждающие эффективность предложенного подхода. В заключении суммируются полученные результаты и раскрываются планы по использованию генератора FRaGenLP для разработки искусственной нейронной сети, способной решать задачи ЛП большой размерности.

• 1.    Метод генерации случайных задач ЛП

Метод генерации случайных задач ЛП, используемый в программе FRaGenLP, позволяет генерировать случайные совместные ограниченные задачи ЛП произвольной размерности n , решение которых заранее неизвестно. Для обеспечения корректности задачи

ЛП система ограничений в	ключает в Г " 1 * 2	себя следующие опорные неравенства : < a < a *                                           — — —           — — —
	- * - * - 2	xn	<	a 0 0	(1)
	* J     + * 2	- * n " + * n	<	0 a (n - 1) + 100

Здесь a ∈ R>0 — положительный масштабирующий коэффициент, являющийся параметром программы FRaGenLP. Количество опорных неравенств равно 2n + 1. Количество случайных неравенств определяется параметром d ∈ !≥0 . Общее количество неравенств m определяется по формуле m = 2 n +1 + d.                                      (2)

Коэффициенты целевой функции задаются вектором c = 0( n, n -1, n - 2,^,1),                                       (3)

где θ ∈ R _{> 0} — положительный постоянный множитель, являющийся параметром программы FRaGenLP и удовлетворяющий условию

θ ≤ a .

Везде далее будем предполагать, что необходимо найти допустимую точку, в которой достигается максимум целевой функции. При количестве случайных неравенств d = 0 генерируется задача ЛП, ограничения которой включают только опорные неравенства (1). В этом случае задача ЛП имеет следующее единственное решение:

x = ( a , ^ , a , a[ 2 ) .

Коэффициенты случайного неравенства a i = ( a i1 , ! , a in ) и правая часть b i вычисляются с помощью функции rand( l, r ), генерирующей случайное вещественное число из интервала [ l, r ] ( l, r e R ; l <  r ) , и функции rsgn(), случайным образом выбирающей число из множества { 1, — 1 } :

a j ^: = rsgnO • rand(0, a max ), b i ^: = rsgnO • ^rand(0, b max ).

Здесь a max ,b mx g R > ₀ — константы, являющиеся параметрами программы FRaGenLP. В качестве знака неравенства всегда выбирается ≤ . Введем следующие обозначения:

Л.Б. Соколинский, И.М. Соколинская f( x ) = Cc, x );

^ =al² !a/ 2 ) ;

. К a, h cnr} - b i\ dist( a i , b i , h cntr ) =  -----_о----- ; a i

n (x, a_t, b ) = x -    ’   —- a.

i                   l ^ i f        i

Формула (7) определяет целевую функцию задачи ЛП. Здесь и далее ! , ! обозначает скалярное произведение векторов. Формула (8) определяет центральную точку ограничивающего гиперкуба , задаваемого первыми 2 n неравенствами системы (1). Формула (9) определяет функцию dist( a i , b i , h_cntr ), вычисляющую расстояние от гиперплоскости a_i , x = b_i до центра ограничивающего гиперкуба. Здесь и далее ! обозначает евклидову норму. Формула (10) определяет вектор-функцию, вычисляющую ортогональную проекцию точки x на гиперплоскость a_i , x = b_i .

Случайное неравенство a_i , x ≤ b_i получается путем генерации координат вектора a_i и свободного члена b_i с помощью датчика псевдослучайных дробно-рациональных чисел. Сгенерированное случайное неравенство добавляется в систему ограничений в том, и только в том случае, когда выполняются следующие условия:

(ai, hcntr) ^ bi;

p < dist( ai, bi, hcntr) < 0;

f (n ( hcntr , ai, bi))> f ( hcntr );

Vl g{1,!,i-1}:-like(ai,bi,al,bl).

Условие (11) требует, чтобы центр ограничивающего гиперкуба являлся допустимой точкой для добавляемого неравенства. Если это условие не выполняется, то вместо неравенства a_i , x ≤ b_i можно взять неравенство - a_i , x ≤- b_i . Условие (12) требует, чтобы расстояние от гиперплоскости a_i , x = b_i до центра h_cntr ограничивающего гиперкуба было больше ρ и меньше θ . Константа ρ ∈ ! _{> 0} является параметром программы FRaGenLP и должна удовлетворять условию ρ < θ , где θ , в свою очередь, удовлетворяет условию (4). Условие (13) требует, чтобы значение целевой функции в точке проекции h_cntr на гиперплоскость a_i , x = b_i было больше, чем в самой точке h_cntr . Это условие в сочетании с (11) и (12) отсекает ограничения, которые не могут повлиять на решение задачи ЛП. Условие (14) требует, чтобы новое неравенство было непохоже на все ранее добавленные, включая опорные. Указанное условие использует булевскую функцию like , определяющую похожесть ( likeness ) двух неравенств a_i , x ≤ b_i и a_l , x ≤ b_l по следующей формуле:

like( a i , b i , a i , b i ) =

a_ia_l a i - a l

< L mvaix ^

b_ib_l a i - a l

< ^Smin *

Константы Lmax, Smin ∈!>0 являются параметрами программы FRaGenLP. При этом параметр Lmax должен удовлетворять условию

L

max

≤ 0.7

(обоснование этому ограничению будет дано ниже). В соответствии с формулой (15) неравенства a_i , x ≤ b_i и a_l , x ≤ b_l считаются похожими, если выполняются следующие два условия:

a_ia_l a i - a l

b_ib _l a i - a l

< L max ;

< S min .

Условие (17) оценивает параллельность гиперплоскостей a_i , x = b_i и a_l , x = b_l , ограничивающих допустимые области исходных неравенств. Для этого сначала вычисляются единичные векторы нормалей e_i = a_ia_i и e_l = a_la_l к гиперплоскостям a_i , x = b_i и a_l , x = b_l . Затем вычисляется норма разности единичных векторов нормалей: δ = e_i - e_l .

Если δ = 0 , то гиперплоскости параллельны. Если 0 < δ < L_max , то гиперплоскости считаются почти параллельными . Условие (18) оценивает «близость» гиперплоскостей a_i , x = b_i и a_l , x = b_l относительно друг друга. Для этого сначала вычисляются нормализованные свободные члены β _i = b_ia_i и β _l = b_la_l . Затем вычисляется модуль их разности σ = β _i - β _l . Если гиперплоскости параллельны и σ = 0 , то эти гиперплоскости совпадают. Если 0 < σ < S_min , то гиперплоскости считаются почти близкими . Два линейных неравенства в R ⁿ считаются похожими , если соответствующие им гиперплоскости являются почти параллельными и почти близкими.

Ограничение (16) для параметра L_max основано на следующем утверждении.

Утверждение 1. Пусть заданы два единичных вектора e,e′ ∈ Rn и угол ϕ<π между ними. Тогда e-e′ =2(1 - cosϕ).

Доказательство. По определению нормы в евклидовом пространстве имеем

IIe  ell  J^(ej  ej)   J^(ej   2ejej + ej )  J^ej   2^ejej + ^ej   V1 2e ,,ej/ jjjjj

Таким образом

|| e - e '|| = ^ 2 (1 - (j,, e‘)).

По определению угла в евклидовом пространстве для единичных векторов имеем ej,e′j= cosϕ.

Подставив правую часть в (20), получаем

|| e - e '|| = 2 ( 1 - cos ^ ) .

Утверждение доказано.

Разумно считать два единичных вектора e , e ′ почти параллельными, если угол ϕ между ними меньше, чем π 4 . В этом случае согласно (19) имеем

II e - e' <  2 1 1 - cos -

I 4

Учитывая, что cos ( П 4 ) ~ 0.707, получаем требуемую оценку:

e - e ′ <  0.7.

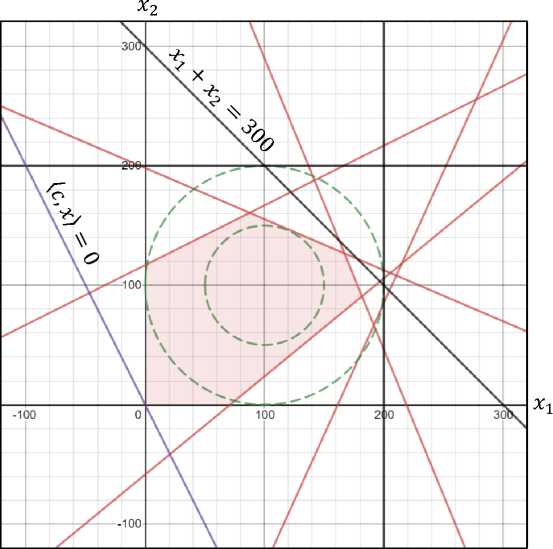
Рис. 1. Случайная задача линейного программирования для n = 2, d = 5, a = 200,0 = 100, p = 50, Smin = 100, Lmax = 0.35, amax = 1000, bmax = 10000 (нарисовано с помощью графического калькулятора Desmos [14])

На рис. 1 представлена случайная задача, сгенерированная программой FRaGenLP в соответствии с выше описанным методом для размерности n = 2 с использованием следующих значений параметров: d = 5 , a = 200 , θ = 100 , ρ = 50, S_min = 100 , L_max = 0.35 , a_max = 1000 , b_max = 10000 . Фиолетовым цветом на рисунке обозначена прямая, определяемая коэффициентами целевой функции; черными линиями обозначены прямые, соответствующие опорным неравенствам; красными линиями обозначены прямые, соответствующие случайным неравенствам. Для наглядности на рисунке также обозначены зелеными пунктирными линиями большая и малая окружности, задаваемые уравнениями ( x 1 - 100 ) 2 + ( x 2 - 100 ) 2 = 100 2 и ( x 1 - 100 ) 2 + ( x 2 - 100 ) 2 = 50 2 соответственно. Любая случайная прямая должна пересекать большую окружность и не пересекать малую окружность в соответствии с условием (12). Полупрозрачным красным цветом выделена область допустимых точек получившейся задачи линейного программирования.

Алгоритм 1. Последовательный алгоритм генерации случайной задачи ЛП

• 1:    input n, d, ct, 6,p, S _m / _n , L _max , ci _max , b _max

• 2:    k := 0

• 3:    A:=[]

• 4:    B:=[]

• 5:    AddSupport(A, B)

• 6:    for j = n ... 1 do C j := 6 ■ j

• 7:    if d = 0 goto 20

• 8:    for j = 1 .n do a j := rsign() ■ rand(0, a _max )

• 9:    b := rsign( ) ■ rand(0, b _max )

• 10:    if (a, h _cntr) < b goto 13

• 11:    for j = 1 ...n do a j := —a j

• 12:    b :=—b

• 13:    if dist(a,b,h _cntr ) < p or dist(a, b, h _cntr ) > 6 goto 8

• ^14:    if /(n(h c„tr ,a_i,b_i)) >/(h c„tr ) goto 8

• 15:    for all (d, S) £ (A,B) do if Hke(a,b,d/b) goto 8

• 16:    A:=A*a

• 17:    B:=B*b

• 18:    k:=k + 1

• 19:    if k < d goto 8

• 20:    output A, B, c 21: stop

• 2.    Параллельный алгоритм генерации случайных задач ЛП

  Неявные циклы с возвратом на метку 8, возникающие на шагах 13–15 алгоритма 1, могут потребовать значительных временных затрат. Так, при генерации задачи ЛП, представленной на рис. 1, возвраты на метку 8 осуществлялись 112581 раз с шага 13, 32771 раз с шага 14, и 726 раз с шага 15. В силу этого генерация большой случайной задачи ЛП на обычном персональном компьютере может длиться несколько суток. Поэтому нами

• 3.    Программная реализация и вычислительные

Описанный метод представлен в виде последовательного алгоритма 1. На шаге 1 вводятся параметры алгоритма. На шаге 2 счетчику случайных неравенств присваивается значение 0. На шаге 3 формируется пустой список строк матрицы A . На шаге 4 формируется пустой список строк свободных членов B . На шаге 5 в списки A и B добавляются коэффициенты и свободные члены опорных неравенств (1). На шаге 6 проверяется количество случайных неравенств d : если d = 0 , то происходит вывод только опорных неравенств, после чего алгоритм заканчивает свою работу. На шаге 7 генерируются коэффициенты целевой функции в соответствии с формулой (3). На шагах 8 и 9 генерируются коэффициенты и свободный член нового случайного неравенства. На шаге 10 проверяется условие (11). Если это условие не верно, то знаки коэффициентов и свободного члена меняются на противоположные (шаги 11, 12). На шаге 13 проверяется условие (12). На шаге 14 проверяется условие (13). На шаге 15 проверяется условие (14). На шаге 16 коэффициенты нового случайного неравенства добавляются в матрицу A . На шаге 17 свободный член нового случайного неравенства добавляется в столбец B . На шаге 18 счетчик неравенств увеличивается на единицу. На шаге 19 проверяется, достигло ли количество неравенств требуемого числа, и, при необходимости, осуществляется переход к следующей итерации. На шаге 20 происходит вывод результатов. Шаг 21 завершает работу алгоритма.

Алгоритм 2. Параллельный алгоритм генерации случайной задачи ЛП

Мастер l-й рабочий (l=1,…,L) M1 input a, d, a, 6, р, Sm/n, Lmax, amax, bmax W1: input n,d,a,6,p,Smin,Lmax,amax,bmax M2 k := 0 W2: if d < 0 goto W37 M3 As = [] W3: As = [] M4 BS==[] W4: Bs:=[ ] M5 AddSupport(As, Bs) W5: AddSupport(As, Bi) M6 for j = П ... 1 do Cj := 6 ■ j W6: for j = 1 .n do begin M7 Ar = [] W7:   aj^ := rsign( ) ■ rand(0, amax'' M8 BR = [ ] W8: end M9 if d > 0 goto M19 W9: b(l) := rsign( ) ■ rand(0, bma3) M10 output As,Bs, c W10: if (а^, hcntr) < b^1^ goto W13 M11 goto M37 W11: for j = 1 .n do Cj := —Cj M12 W12: bm := —b^ M13 W13: if dist(a(i), b(i),hcntr) < p goto W6 M14 W14: if dist(a(i), b(i),hcntr) > 6 goto W6 M15 W15: if /■(n(hCntr,a(i),b(i))) > f(hCntr) goto W6 M16 W16: for all (a, b) ё (As,Bi) do begin M17 W17: if like(a(i),b(i),a, b) goto W6 M18 W18: end M19 RecvFro'mAllWorkers(al-1'', b^1^, ., al'L'', b(C)^ W19: SendToMaster(a®, b®) M20 for l = 1.L do begin W20: M21 is_like := false W21: M22 for all (a, b) ё (Ar,Br) do begin W22: M23 if like(a®,b®,a, b) then begin W23: M24 is_like := true W24: M25 goto M28 W25: M26 end W26: M27 end W27: M28 if is_like continue W28: M29 Ar := Ar * a® W29: M30 BR := BR * b" W30: M31 k:=k + 1 W31: M32 if k = d goto M34 W32: M33 end W33: M34 SendT oAllWorkers(k') W34: RecuFromMaster^') M35 if k < d goto M19 W35: if k < d goto W6 M36 output As,Bs,AR,BR,c W36: M37 stop W37: stop была разработана параллельная версия генератора задач FRaGenLP для кластерных вычислительных систем. Эта версия представлена в виде алгоритма 2. Данный алгоритм разработан в соответствии с моделью параллельных вычислений BSF [15], использующей парадигму «мастер-рабочий» [16]. В соответствии с этой моделью узел-мастер является центром управления и коммуникации. Все узлы-рабочие выполняют один и тот же код, но над разными данными.

Сначала рассмотрим шаги, выполняемые узлом-мастером. На шаге M1 мастер считывает параметры задачи. На шаге M2 счетчику случайных неравенств присваивается значение 0. В параллельной версии опорные и случайные неравенства хранятся в разных списках. На шагах M3 и M4 мастер создает пустые списки AS и BS для коэффициентов и свободных членов опорных неравенств. На шаге M5 в эти списки добавляются опорные неравенства (1). На шаге M6 генерируются коэффициенты целевой функции в соответствии с формулой (3). На шагах M7 и M8 создаются пустые списки AR и BR для коэффициентов и свободных членов случайных неравенств. На шаге M9 проверяется количество случайных неравенств d : если d ≤ 0 , то происходит вывод только опорных неравенств (шаг M10), после чего мастер заканчивает свою работу (переход с шага M11 на шаг M37). Если d > 0 , то мастер продолжает свою работу. На шаге M19 мастер получает по одному случайному неравенству от всех рабочих. Рабочие обеспечивают для своих неравенств выполнение свойств (11)–(13) и проверяют их похожесть на все опорные неравенства. Мастер в цикле M20–M33 проверяет все поступившие случайные неравенства на похожесть с ранее включенными в списки AR и BR случайными неравенствами (вложенный цикл M22–M27). Если обнаруживается похожее случайное неравенство (шаги M23– M26), то новое неравенство игнорируется, и осуществляется переход к проверке следующего поступившего неравенства (шаг M28). Если похожих неравенств не нашлось, новое случайное неравенство добавляется мастером в списки AR , BR (шаги M29, M30), и счетчик случайных неравенств увеличивается на единицу (шаг M31). Если количество неравенств достигло заданного значения (шаг M32), то происходит выход из внешнего цикла, в противном случае проверки продолжаются. После завершения проверок и добавлений поступивших случайных неравенств мастер рассылает всем рабочим общее количество случайных неравенств, включенных в систему на данный момент (шаг M34). Если это количество не достигло требуемого, то происходит переход к следующей глобальной итерации (шаг M35), в противном случае мастер выводит результаты и завершает свою работу (шаги M36, M37).

Теперь рассмотрим шаги, выполняемые l-м рабочим . На шаге W1 рабочий считывает параметры задачи. На шаге W2 проверяется количество случайных неравенств d : если d ≤ 0 , то рабочий немедленно заканчивает свою работу, в противном случае создаются пустые списки A _S и B _S для коэффициентов и свободных членов опорных неравенств (шаги W3, W4). На шаге W5 в эти списки добавляются опорные неравенства (1). На шагах W6–W9 рабочий генерирует новое случайное неравенство. На шаге W10 проверяется условие (11). Если это условие не верно, то знаки коэффициентов и свободного члена сгенерированного неравенства меняются на противоположные (шаги W11, W12). Шаги W13– W15 проверяют условия (12), (13). Шаги W16–W18 проверяют похожесть сгенерированного неравенства на опорные неравенства с использованием формулы (14). Если хотя бы одно из этих условий не выполняется, осуществляется переход на шаг W6 для повторной генерации нового случайного неравенства. Если все указанные условия выполнены, рабочий пересылает мастеру построенное случайное неравенство (шаг W19). После этого рабочий ждет, когда мастер пришлет ему новое значение счетчика случайных неравенств k (шаг W34). Если k меньше заданного количества случайных неравенств d , то происходит переход на шаг W6 для генерации следующего случайного неравенства (шаг W35), в противном случае рабочий завершает свою работу (шаг W37).

эксперименты

Параллельный алгоритм 2 был нами реализован на языке C++ с использованием параллельного BSF-каркаса [17, 18]. BSF-каркас базируется на модели параллельных вычислений BSF [15] и инкапсулирует в проблемно независимой части своего кода все аспекты, связанные с распараллеливанием программы с помощью библиотеки MPI [19]. BSF-каркас требует преобразования алгоритма в форму, работающую со списками с использованием функций высшего порядка Map и Reduce , определяемых формализмом Бирда—Миртенса (Bird–Meertens formalism) [20]. Это преобразование было сделано следующим образом. Длина списков Map и Reduce устанавливалась равной количеству рабочих MPI-процессов. Элементы списка Map определялись как пустые структуры:

struct PT_bsf_mapElem_T {}.

Каждый элемент списка Reduce хранил коэффициенты и свободный член одного случайного неравенства a , x ≤ b :

struct PT_bsf_reduceElem_T {float a[u]; float b}.

Каждый рабочий MPI-процесс генерировал по одному случайному неравенству с помощью функции PC_bsf_MapF, которая включала в себя шаги W6–W18 алгоритма 2. Неравенство, удовлетворяющее всем условиям, записывалось рабочим в локальный список Reduce, состоящий из одного элемента. Мастер получал от каждого рабочего сгенерированные элементы и помещал их в свой список Reduce (это выполнялось проблемно-независимой частью BSF-каркаса). Полученные элементы вручную проверялись на похожесть с ранее добавленными случайными неравенствами и, при отсутствии конфликтов, добавлялись в списки AR, BR. Указанная обработка (шаги M20–M33) была нами реализована в предопределенной функции PC_bsf_ProcessResults. Исходные коды параллельной программы FRaGenLP свободно доступны в сети Интернет по адресу

С использованием указанной программы нами были проведены масштабные вычислительные эксперименты на вычислительном кластере «Торнадо ЮУрГУ» [21], характеристики которого приведены в табл. 1. Вычисления проводились для размерности n , равной 3 000, 5 500 и 15 000. Количество неравенств, соответственно, составляло 6 301, 10 001 и 31 501. Из них случайных: 300, 500, 1500 соответственно. Во всех экспериментах были установлены следующие значения параметров, введенных в разделе 1: длина ребра ограничивающего гиперкуба α = 200 , радиус большой гиперсферы θ = 100 , радиус малой гиперсферы ρ = 50 , верхняя граница «почти параллельности» для гиперплоскостей L _max = 0.35 , минимальная допустимая близость для гиперплоскостей S _min = 100 , максимальное допустимое абсолютное значение при генерации коэффициентов случайных неравенств a _max = 1000 , максимальное допустимое абсолютное значение при генерации правых частей случайных неравенств b _max = 10000 . Результаты экспериментов представлены на рис. 2. Время генерации случайной задачи ЛП с 31501 ограничениями на конфигурации из одного узла-мастера и одного узла-рабочего составило 12 минут. На конфигурации из одного узла-мастера и 170 узлов-рабочих генерация такой же задачи заняла 22 секунды. Анализ результатов показывает, что граница масштабируемости предложенного алгоритма существенно зависит от размерности задачи (под границей масштабируемости здесь понимается максимум кривой ускорения). При n = 3000 граница масштабируемости составила приблизительно 50 процессорных узлов. Для задачи размерности n = 5000 эта

Таблица 1. Характеристики кластера «Торнадо ЮУрГУ»

Количество процессорных узлов	480
Процессоры	Intel Xeon X5680 (6 cores 3.33 GHz)
Количество процессоров в узле	2
Оперативная память узла	24 GB DDR3
Соединительная сеть	InfniBand QDR (40 Gbit/s)
Операционная система	Linux CentOS

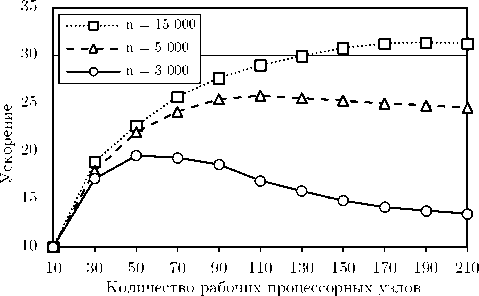
Рис. 2. Графики ускорения алгоритма FRaGenLP для различных размерностей

граница увеличилась до 110 узлов, а на задаче размерности n = 15000 она достигла 200 узлов. Дальнейшее увеличение размерности задачи приводило к нехватке оперативной памяти на процессорных узлах. Следует отметить, что граница масштабируемости предложенного алгоритма также существенно зависит от количества случайных неравенств. Увеличение этого числа в 10 раз приводило к двукратному уменьшению границы масштабируемости. Это объясняется тем, что при увеличении количества узлов-рабочих значительно возрастала доля последовательных вычислений, выполняемых узлом-мастером на шагах M20–M27, в течение которых узлы-рабочие простаивали.

Заключение

В данной работе представлен параллельный алгоритм FRaGenLP для генерации случайных совместных ограниченных задач ЛП на кластерных вычислительных системах. Генерируемые системы ограничений наряду со случайными неравенствами включают в себя стандартный набор неравенств, называемых опорными. Опорные неравенства гарантируют ограниченность допустимой области задачи ЛП. С геометрической точки зрения допустимая область опорных неравенств представляет собой гиперкуб, прилежащий к осям координат, у которого срезана дальняя от центра координат вершина. Целевая функция задается определенным образом, так, чтобы ее коэффициенты монотонно убывали. Коэффициенты и свободные члены случайных неравенств генерируются с помощью датчика случайных чисел. Если допустимая область сгенерированного случайного неравенства не включает в себя центр ограничивающего гиперкуба, то знак неравенства меняется на противоположный. Однако не всякое случайное неравенство включается в систему. Отклоняются случайные неравенства, которые не могут повлиять на решение задачи ЛП при заданной целевой функции. Также отклоняются все неравенства, для которых ограничивающая гиперплоскость пересекает малую гиперсферу, расположенную в центре ограничивающего гиперкуба (это гарантирует совместность). Кроме того, отклоняется всякое случайное неравенство, «похожее» на хотя бы одно неравенство, уже добавленное в систему (включая опорные). Для определения «похожести» неравенств введены две формальные метрики: почти параллельности и близости соответствующих им гиперплоскостей. Параллельный алгоритм спроектирован на базе модели параллельных вычислений BSF, использующей парадигму «мастер-рабочий». В соответствии с этой моделью узел-мастер является центром управления и коммуникации. Все узлы-рабочие выполняют один и тот же код, но над разными данными. Параллельная реализация выполнена на языке C++ с использованием параллельного BSF-каркаса, инкапсулирующего в проблемно независимой части своего кода все аспекты, связанные с распараллеливанием программы с помощью библиотеки MPI. Исходные коды разработанной параллельной программы свободно доступны в сети Интернет по адресу С использованием этой реализации были проведены масштабные вычислительные эксперименты на кластерной вычислительной системе. Проведенные эксперименты показали, что алгоритм FRaGenLP демонстрирует для размерности 15 000 хорошую масштабируемость вплоть до 200 процессорных узлов. Случайная задача ЛП, включающая в себя 31 501 неравенство, была сгенерирована на конфигурации из 171 процессорного узла за 22 секунды. На одном процессорном узле для этого потребовалось 12 минут. Разработанную программу предполагается использовать для генерации 70 000 образцов для обучения искусственной нейронной сети, способной быстро решать большие задачи ЛП.

Исследование выполнено при финансовой поддержке РФФИ (проект № 20-07-00092-а) и Министерства науки и высшего образования РФ (государственное задание FENU-2020-0022).