О генерации третьей гармоники автоколебаний в схемах Хартли и Мейснера

Трехточка Хартли (индуктивная трехточка) – одна из основных схем построения радиочастотных генераторов колебаний, наряду со схемами Мейснера и Колпитца [1–3]. В квазигармониче-ском приближении динамика этих автоколебательных систем (АКС) адекватно описывается в рамках метода медленно меняющихся амплитуд. При высоких уровнях возбуждения для моделирования автоколебаний приходится использовать численные методы. Но этот путь для генератора Хартли сопряжен с определенными трудностями, поскольку математическая модель

генератора формулируется как задача Коши для нелинейного дифференциального уравнения, не разрешенного относительно старшей производной.

В настоящем сообщении предлагается комбинированный численно-аналитический метод моделирования АКС, базирующийся на представлении системы в виде совокупности осцилляторов основной частоты и ее гармоник. Ведущий осциллятор генерирует строго монохроматические автоколебания в дискретном времени в соответствии с алгоритмом (разностным уравнением движения), представленным в статье [4]. Осцилляторы гармоник – линейные осцилляторы с узкополосным возбуждением.

Основное внимание уделено генерации третьей гармоники в схеме Хартли в сравнении с третьей гармоникой генератора Мейснера.

1. Автоколебания в схеме Хартли

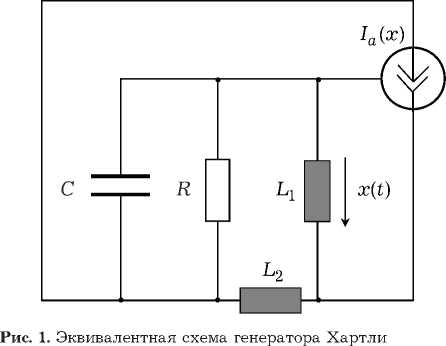
Эквивалентная высокочастотная схема генератора представлена на рис. 1.

Математическая модель АКС в форме дифференциального уравнения движения, составлен-

ного на основе ее схемы, имеет вид

d ² x dt ²

to o dx

Q dt

+ to o x —

nZ ₀ d ³ to o dt ³

I_a ( x ),

где to o , Q и Z o — собственная частота, добротность и характеристическое сопротивление LRC -контура ( L = L i + L ), n = L i L 2 / ( L i + L 2 )² - коэффициент автотрансформаторной связи. Активный трехполюсник (генератор тока, управляемый напряжением) представлен в уравнении (1) вольтамперной характеристикой I_a ( x ). В дальнейшем будем использовать ее в форме I a ( x ) = g 0 u ( x ), где g o - крутизна характеристики в малосигнальном (линейном) приближении, а для нелинейности примем «классическую» ап-

ния (2), его можно свести к совокупности двух первой x ₁( t ) и третьей x ₃ ( t ) гармоник:

d2 xi   too dt2    Qdt d2 xg   too dt2    Qdt

22 dx

+ tooxi = ytoos(ai)      , dt

^{+ to} o ^x 3 =

проксимацию

x ³

u ^{( x} ) = ^x " T

.

Дифференциальное уравнение (1) не разрешено относительно старшей производной, в связи с чем возникают определенные проблемы с его численным интегрированием. Здесь предлагается один из способов их устранения.

Для удобства дальнейших преобразований уравнение (1) запишем в виде

d2x d?+

to o dx

Q dt

to o x = Yto o dt z ( x ( t ) ) ,

где обозначено

z ( x ( t ) ) = -to o ²

d ²

— u ( x ( t ) ) , dt ²

Y = ng o Z o .

Константа у связана с параметром превышения порога генерации соотношением p = у Q (порог: Р = ^1).

В гармоническом приближении для колебаний x ( t ) = x 1 ( t ) = a i cos ( to o t )

с амплитудой a^ функция u (xi(t)) в правой части уравнения (2) представляется рядом Фурье u (xi(t)) = ui(ai) cos (toot) + uз(ai) cos (3to01),

где

I-,      12 I /2а ui(ai) = I 1 - — ai I ai = s(ai)ai, u3(ai) = - ai.

Дифференцирование в функциях, входящих в правую часть уравнения (2) в дальнейшем проводится с учетом медленности амплитуды a1 – производные амплитуды обнуляются. Поэтому приближенное выражение для осциллирующей функции (3) имеет вид z (xi(t)) = ui(ai) cos (toot) + 9uз(ai) cos (3to01) • (4)

Теперь приравнивая соответствующие гармоники в правой и левой частях уравнения движе-

- 27 yto o u 3 ( a i ) sin ( 3 to o t ) .

Для анализа генерации первой гармоники линеаризованным осциллятором (5) воспользуемся его дискретной моделью, предложенной в работе [4]. Предполагая дискретизацию времени с интервалом А в уравнение (5) вводится безразмерная временная переменная т = t / А :

d2x      dxdx

---1 + 2nv —1 + 4n2Qoxi = 2nv ps (a2)—1.(7)

d т2       d т

Здесь Q o = to o / to d — собственная частота, измеряемая в единицах частоты дискретизации to d = 2 п / А ; v = Q o / Q — полоса резонатора.

На временной сетке т _n = n дифференциальное уравнение (7) заменяется разностным уравнением

x [ n ] - 2 a cos ( 2 nQ o ) x [ n - 1] +

+ a ² x [ n - 2] = e ( 1 - o.5 w [ n - 1] ) x                 (8)

x (cos (2nQo) x[n - 1] - x[n - 2]), где e = 2navp и a = exp(-nv) — параметры глубины обратной связи и диссипативности. При этом мощность автоколебаний w = a2 /2 вычисляется по мгновенным значениям осцилляций:

w [ n ] =-----5"1------ x

2 sin² ( 2 nQ _o )

x ( x ²[ n ] - 2 cos ( 2 nQ o ) x [ n ] x [ n - 1] + x ²[ n - 1] ) •

Таким образом, дискретный осциллятор (8)– (9) моделирует первую гармонику автоколебаний. На рис. 2 для иллюстрации представлен амплитудный спектр a i ( Q ) установившихся автоколебаний и процесс установления амплитуды a i [ n ] = xj 2 w [ n ] (на вставке). Параметры автоколебательной системы: Q o = o.15, Q = 3o, p = 7.

Колебания линейного осциллятора третьей гармоники (6) с квазистационарным возбуждением проанализируем методом медленно меняющихся амплитуд, в рамках которого осцилляции представляются в виде

x g ( t ) =

= I А з (t ) exp ( j 3 to o t ) + ¹ A 3 (t ) exp ( - j 3 to o t ) ,

а для «медленной» комплексной амплитуды A ₃( t ) записывается укороченное уравнение

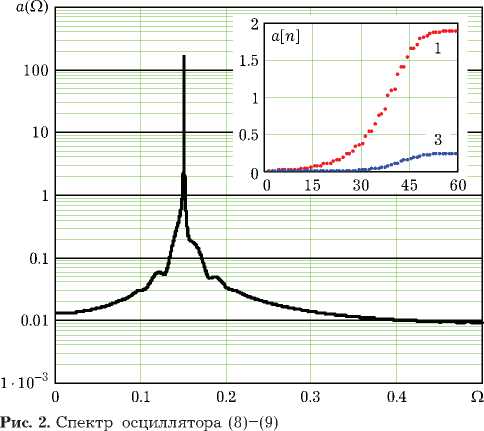
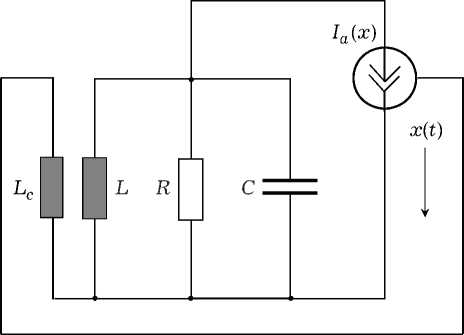
Рис. 3. Эквивалентная схема генератора Мейснера

j 6 ® 0 [ "77 A 3 (t ) + A A A 3 (t ) ^ -

^ dt       2 Q      )

• - ^{8 to} ° A 3 ⁽ t ) = j27 4^ 2^u 3 ( ^a 1 ).

С учетом того, что Q >>  1 и | dA 3 / dt | << to° | А з| первыми двумя слагаемыми в этом уравнении можно пренебречь. Тогда

( 3 ^ ³

а з ( t ) = [ 2 ) ^Y u з ( a 1 ( t )).                                 (1°)

График процесса установления амплитуды третьей гармоники показан на вставке рис. 2.

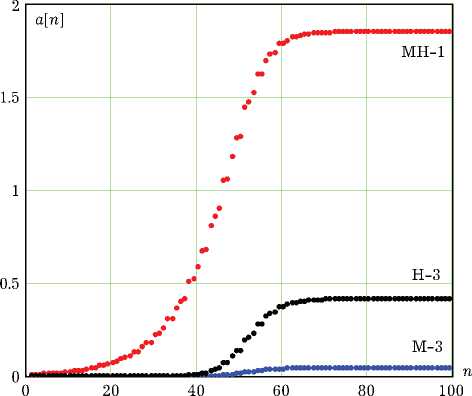
Рис. 4. Временные зависимости амплитуд гармоник автоколебаний

• 2.    Автоколебания в схеме Мейснера

Эквивалентная высокочастотная схема генератора Мейснера представлена на рис. 3.

Математическая модель АКС в форме дифференциального уравнения движения, составленного на основе ее схемы, имеет вид d2 x ton dx 2 a d- т x

+ to 3T^+to ° x = n ^to ° ^Z° "^Ia ⁽ x )’           ⁽¹¹⁾

dt2   Q dt                dt где n = Lc / L — коэффициент трансформаторной связи. Активный трехполюсник имеет ту же вольтамперную характеристику Ia (x), что и в схеме Хартли.

Запись уравнения (11) в обозначениях уравнения (2) имеет вид d2x to, dx 2 d , z

+ 7?    + to° x = Yto° "T+z (x(t)), dt2   Q dt             dt где, в отличие от (3), z (x(t)) ^ u (x(t)) .

Теперь в гармоническом приближении выражение для осциллирующей функции (12) имеет вид z (x1(t)) = U1(a1) cos (to°t) + uз(a1) cos (3to°t).

Поэтому для схемы Мейснера осциллятор первой гармоники (5) сохраняется, а в осцилляторе третьей гармоники (6) изменяется возбуждение:

d ² x ₃

dt ²

. ^to ° ^dx3 .   2              2

+----+ tog x ^ = — 3 ytog u^ ( a ^ )sin ( 3 tog t ) .

Q dt

Отсюда, аналогично тому, как это сделано для уравнения (6), находим амплитуду третьей гармоники автоколебаний в схеме Мейснера:

а з ( t ) = -Y u з ( a 1 ( t )). (13) 8

Из сравнения амплитуд (10) и (13) следует очевидный вывод о том, что при одинаковых амплитудах первых гармоник амплитуда третьей в схеме Хартли в девять раз выше, чем в схеме Мейснера.

На рис. 4 приведены графики процессов установления амплитуд гармоник в рассмотренных схемах с параметрами Q ° = 0.19, Q = 3°, p = 7:

МН-1 – первая гармоника, Н-3 – третья гармоника в схеме Хартли, М-3 – третья гармоника в схеме Мейснера.

Заключение

Предложенный метод моделирования АКС дает наглядное представление о причине повышенного уровня гармоник в схеме автогенератора с автотрансформаторной связью (Хартли) по сравнению со схемой с трансформаторной связью (Мейснера). Это наличие двукратного дифференцирования в цепи сигнала в цепи обратной связи.

В рамках классификации теории нелинейных колебаний представленная модель соответству- ет улучшенному первому приближению метода усреднения.