О генерации волн толмина-шлихтинга в пограничном слое вязкого теплопроводного газа
Бесплатный доступ
Показано, что закон возникновения турбулентности в вязком теплопроводном газе описывает один из механизмов генерации волн Толмина-Шлихтинга в пограничном слое на передней кромке пластины. Отмечается, что найденное аналитическое выражение для пульсаций давления на передней кромке пластины качественно верно описывает зависимость интенсивности возмущений от средней скорости набегающего потока и частоты возмущений, установленную экспериментально в работах Качанова, Козлова и Левченко
Волны толмина-шлихтинга, закон возникновения турбулентности, вязкий теплопроводный газ
Короткий адрес: https://sciup.org/143165273
IDR: 143165273
Текст научной статьи О генерации волн толмина-шлихтинга в пограничном слое вязкого теплопроводного газа
Электронный журнал «Техническая акустика»
В работах Качанова, Козлова и Левченко [1] установлена важная роль передней кромки пластины в формировании вихревых волн пограничного слоя — волн Толмина-Шлихтинга (рис. 1).
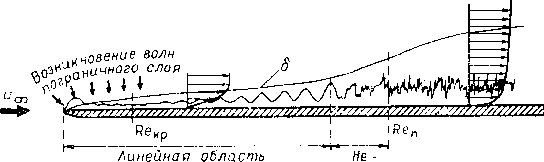
линейная область
Рис. 1. Схема основных стадий процесса перехода в пограничном слое. Рисунок из работы [1]
Передняя кромка пластины является типичной локальной неоднородностью, где претерпевают достаточно резкие изменения поле возмущений и средний поток. Но до конца не ясен механизм усиления поля возмущений на передней кромке пластины и генерации волн Толмина-Шлихтинга.
Рассмотрим механизм усиления поля возмущений на передней кромке пластины и генерации волн Толмина-Шлихтинга, привлекая закон возникновения турбулентности , полученный в работе [2].
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Приведем полученный в работе [2] закон возникновения турбулентности в виде dp = as 2 d p + ( v • ( as 2 grad p - gradp ) + ( k - 1 ) Ф ) dt , (1)
где as — адиабатное и изоэнтропное значение скорости звука; p, p — давление и плотность газа; Ф — функция, учитывающая диссипацию энергии и теплообмен ж д д T д
Ф = —I X— 1 + — д x v д x J д у
"I T
V д y J
д
+ — дz
+
+ ц<
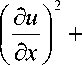
2^2 2 й J
2 д w д v
+ [~д у +1Z у
+
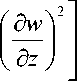
(д v д и А
+ +
V д x д у J
(д u 1 w А 2
+ I + I
^д z д x J
+
2 д и д v д w
--+ — + —
3 ^д x д у д z J
;
Т — температура газа; V — вектор скорости газа с проекциями и , v , w на оси декартовой системы координат x , у , z соответственно; X — коэффициент теплопроводности; ц — коэффициент динамической вязкости; t — время; k — показатель адиабаты.
Из закона возникновения турбулентности (1) следует, что в вязком теплопроводном ди ди д v д v газе при возникновении градиентов скорости потока —, —, —,— на передней кромке дx ду дx ду пластины вследствие прилипания потока на стенке пластины (и = 0, v = 0), будут возникать возмущения давления dp в плоскости xy, которые генерируют вихревые волны.
В работе [1] приведены результаты экспериментов по генерации волн Толмина-Шлихтинга на плоской пластине. В поток, набегающий на пластину, вводились колебания малой амплитуды с помощью вибрирующей ленты. В приведенных экспериментах установлено, что величина скачка амплитуды возмущений ^, т.е. отношение среднеквадратичных интенсивностей продольной компоненты пульсаций и' в районе передней кромки и в набегающем потоке, характеризующая мощность генератора волн Толмина-Шлихтинга, сильно зависит от частот трансформирующего возмущения и от скорости потока (рис. 2, 3). Из рис. 2, 3 следует обратно пропорциональная зависимость интенсивности возмущения от частоты и прямо пропорциональная от скорости потока.
Покажем, что установленные в работе [1] закономерности генерации волн Толмина-Шлихтинга на передней кромке пластины вытекают из закона возникновения турбулентности (1). Закон возникновения турбулентности (1) в правой части включает два члена. Первый член является линейным и описывает акустические соотношения между плотностью и давлением газа. Второй член является нелинейным и учитывает диссипацию энергии и теплообмен в вязком теплопроводном газе. Рассмотрим изменение давления вблизи передней кромки пластины при x«0, обусловленное нелинейным членом в законе (1), когда пограничный слой только начинает формироваться. При этом допустим, что:
-
- разностью конвективных производных плотности и давления, как величинами второго порядка малости, можно пренебречь;
-
- температурные поля еще не сформировались и ими можно пренебречь;
-
- составляющие скорости v , w только начинают формироваться и их
производными также можно пренебречь.
Вблизи передней кромки пластины формируются градиенты скорости u , u .
д x д у
Вследствие прилипания потока на стенке пластины (и = 0) градиент скорости и вдоль оси y будет значительно выше градиента вдоль оси х. Поэтому можно пренебречь u в дx ди сравнении с . В результате из (1) получим ду dP = Ц(k-Ч^ 1дУ )
dt.
Представим скорость как сумму скорости среднего потока и пульсационной составляющей, изменяющейся по гармоническому закону и = и, • и' = и, I ит cos at, (3) где и — скорость набегающего потока: и 'т — амплитуда пульсационной составляющей скорости; щ — круговая частота; t — время.
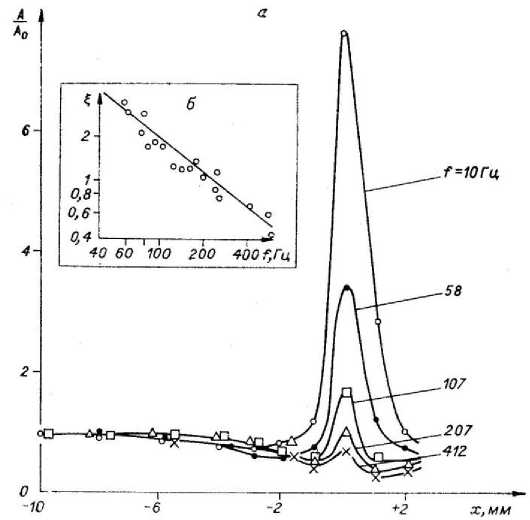
Рис. 2. Скачок интенсивности возмущений на передней кромке пластины; а — изменение амплитуды возмущений различных частот с координатой ( х — координата вдоль пластины, х >0 — над пластиной: х <0 — перед пластиной); б — зависимость скачка интенсивности возмущений от частоты. Рисунок из работы [1]
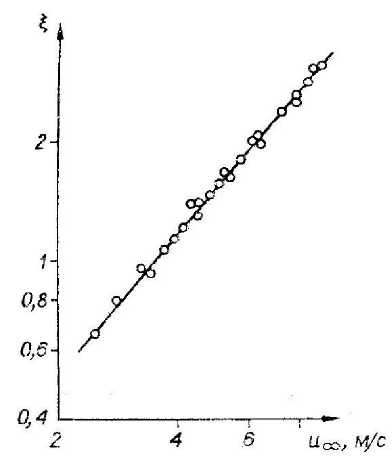
Рис. 3. Зависимость скачка интенсивности возмущения на передней кромке пластины от скорости потока. Рисунок из работы [1]
Подставим выражение скорости (3) в (2) и проинтегрируем по времени. В результате получим
Д p = p ( k - 1 )
( д u L
Иy )
д t + 2 .^ m. 1
ду ду го
sin го t + —
1 ( д и
‘
m
2 1 д у )
Д t + —
1 ( д и
‘ V
m
4 1 д У )
— sin 2 го t го
Учитывая, что в проведенных экспериментах [1] амплитуды возмущений скорости не превышали значений
A m = -m < 0,25%, «
пренебрежем в выражении (4) величинами второго порядка малости — члены третий и четвертый в квадратных скобках.
Скорость в пограничном слое меняется от значения во внешнем потоке до нуля на стенке пластины. Для оценки заменим производные скорости их средними значениями
д -^ u^. д и m -mk
ду д’ ду 8 ’
где 5 — толщина пограничного слоя.
Подставляя выражения (6) в (4), получим
и и 2
Д t + ' ^m sin го t
5 2 го
.
Полученное выражение описывает пульсации давления, возникающие на передней кромке пластины, под действием которых происходит генерация волн Толмина-Шлихтинга.
Анализ полученного выражения (7) позволяет отметить следующее:
-
- пульсации давления на передней кромке пластины будут возникать и при отсутствии возмущений скорости u ′ = 0 , то есть процесс изначально является неустановившимся;
-
- при наличии в набегающем потоке возмущений скорости u ′ , изменяющихся по гармоническому закону, на передней кромке пластины будет возникать составляющая пульсации давления, пропорциональная средней скорости потока u ∞ и обратно пропорциональная круговой частоте ω ; эта составляющая пульсации давления будет порождать на передней кромке пластины пульсации скорости потока, зафиксированные экспериментально в работе [1] и приведенные на рис. 2, 3.
ЗАКЛЮЧЕНИЕ
-
1. Найденное аналитическое выражение для пульсаций давления на передней кромке пластины показывает, что при наличии в набегающем потоке возмущений скорости u ′ , изменяющихся по гармоническому закону, на передней кромке пластины будет возникать составляющая пульсации давления, пропорциональная средней скорости потока u ∞ и обратно пропорциональная круговой частоте ω .
-
2. Полученное выражение качественно верно описывает зависимость интенсивности возмущений от средней скорости набегающего потока и частоты возмущений, установленную экспериментально в работах Качанова, Козлова и Левченко при генерации волн Толмина-Шлихтинга в пограничном слое.
Список литературы О генерации волн толмина-шлихтинга в пограничном слое вязкого теплопроводного газа
- Качанов Ю. С., Козлов В. В., Левченко В. Я. Возникновение турбулентности в пограничном слое. -Новосибирск: Наука, 1982. -151 с.
- Воронков С. С. О законе возникновения турбулентности в вязком теплопроводном газе. Электронный журнал «Техническая акустика», http://www.ejta.org, 2016, 6.


