О генераторах динамического хаоса на основе модифицированной модели Лоренца

1. Модифицированная система Лоренца

Считается, что известная модель Лоренца [1] dX --= -оX + оY, dt dY --= - Y + rX - XZ,                        (1) dt dZ    „ --= - bZ + XY dt послужила отправным пунктом развития хаотической динамики [2]. Несмотря на весьма значительное число публикаций, посвященных исследованию модели, интерес к ней и в настоящее время поддерживается на высоком уровне [3].

Анализ системы уравнений (1) с позиций электронной схемотехники позволяет предложить схему генератора Лоренца , изображенную на рис. 1 (переключатель в положении П₁).

Схема содержит интегрирующие RC -цепи с системными функциями H i ( p ) = 1 / ( p т i + 1), операционные усилители с коэффициентами передачи k_i , перемножители и сумматор. Часть схемы, расположенная выше пунктирной линии, представляет собой апериодический усилитель, нижняя часть – инерционную нелинейную цепь обратной связи с двумя входами. По классификации П.С. Ланды [4; 5] подобные системы относится к генераторам с инерционным самовозбуждением.

Изменим схему цепи обратной связи, превра- тив ее в одновходовую, переведя переключатель в положение П2 . Преобразованную таким образом автоколебательную систему назовем модифицированным генератором Лоренца (МГЛ) [6].

Динамика МГЛ описывается следующими уравнениями состояния для нормированных напряжений Un (t)

dU 1 = dt	1 k --U 1 + 1 U 2 , т 1         т 1
dU 2 = dt	--U 2 + — ( 1 - U 3 ) U 1 , т 2        т 2	(2)
dU 3 = dt	- — U 3 + k 3 U 2 . т 3        т 3

Здесь напряжения нормированы так, что выходы перемножителей связаны с их входами соотношением U_p = U y U 2 . Формально уравнения (2) содержат шесть параметров, но нормировка времени и двух напряжений позволяет сократить их число до четырех. В частности, в стандартной модели Лоренца используются обозначения о = Т 2 / т 1 , b = Т 2 / Т 3 , r = k^, а kkк з ^ = 1.

Результаты численного интегрирования уравнений (2) позволяют сделать вывод о том, что в МГЛ реализуются режимы как регулярных, так и хаотических автоколебаний. Для примера на рис. 2, а и рис. 2, б приведены усредненные амплитудные спектры U 1 (ro) напряжения U 1 ( t )

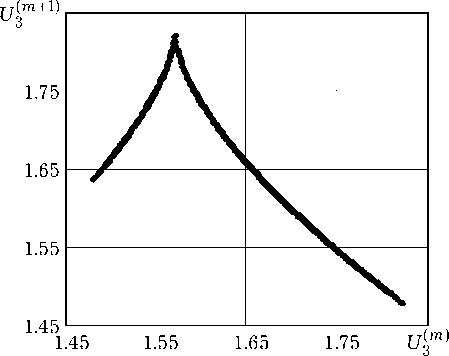
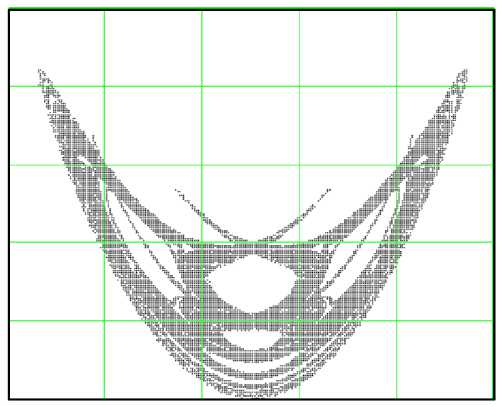
Рис. 3. Отображение первого возвращения

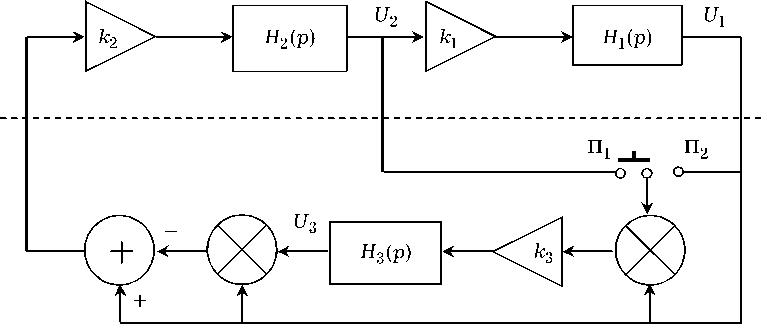
Рис. 1. Схема генератора Лоренца

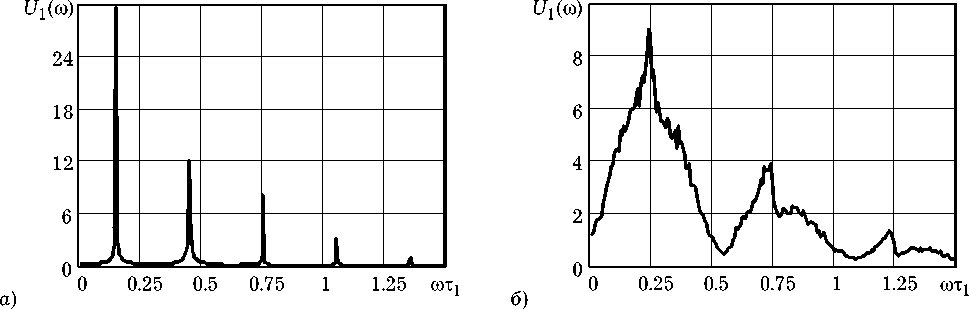
Рис. 2. Усредненный амплитудный спектр напряжения в МГЛ

в генераторе с параметрами k i = 0.45, k 2 = 22.73, k s ^T 1 ^T - 1 = 1, ^т 2 = 9.1^Т 1 , а также Т 3 = 10т 1 (рис. 2, а ) или Т 3 = 3.33Т 1 (рис. 2, б ).

Очевидно, что первый из спектров, состоящий из дискретных линий, отвечает режиму периодических автоколебаний. В то время как, спектр на рис. 2. б в соответствии с прагматическим определением хаоса указывает на режим хаотических автоколебаний.

Качественно характеристики динамического хаоса в МГЛ близки к характеристикам анало- гичных процессов в стандартной системе Лоренца. Например, степень сжатия фазового объема аттрактора характеризует представленное на рис. 3. отображение первого возвращения. Оно получено на основе последовательности координат U3(m) точек в сечении Пуанкаре поверхности kgU2 - U3 = 0. Общий вид графика на рис. 3 полностью соответствует графику отображения первого возвращения в стандартной модели Лоренца [7].

Таким образом, генератор, определяемый уравнениями состояния (2), представляет собой простую радиофизическую систему с режимом хаотических автоколебаний, пригодную для практических применений в численных экспериментах по нелинейной динамике. Кроме того, он допускает переход к дискретному времени без введений в схему дополнительных временных задержек.

• 2.    ДВ-генератор с инерционной нелинейностью

Систему уравнений состояния (2) удобно использовать при моделировании автоколебаний методами численного интегрирования задачи

Коши [8]. Но при переходе к дискретному времени ее целесообразно преобразовать, исключив из первых двух уравнений переменную U2(t). В результате получим систему d2x dx 22

+ 2to       + to-r-. x — k^ (D-t-j dt2     sdt    p pp dy               2

— — -topy + k topx . c3c dt

( 1 - y ) x ,

Здесь x ( t ) — U i (t ), y ( t ) — U 3 ( t ) и введены обозначения

2to s —--+     , т1    t2

to c —     , t3

^to p ^— J — и ^kp ^{— k} 1 k 2 • N ^T 1 ^T 2

Первое из уравнений системы (3) запишем в форме интегрального Вольтера второго рода t

X ( t ) — J f ( x (t), у (т)) h ( t - t) d т + X ( t ) •              (4)

где f (x, y) — (1 - У) x, функция времени X(t) описывает свободный процесс в линейной системе (при kp — 0). Ядро уравнения (4) h(t - t) — импульсная характеристика, удовлетворяющая дифференциальному уравнению d2h   dh 22

—-—+ 2 to _s    + to p h — k p to p 5( t )

dt ²       dt   ^{p pp}

с дельта-функцией в правой части и нулевыми начальными условиями. Отметим, что свободный процесс X ( t ) удовлетворяет однородному уравнению (5) и зависит от начальных условий.

Решением (5) при t > 0 является функция h (t) — kp

. ^p = exp ( -to s t ) sinh Uto 2 - to p t ) • (6)

J to 2 - to 2 sp

Нетрудно показать, что отсчеты характеристики (6) на равномерной временной сетке t n — n A t при n > 2 удовлетворяют разностному уравнению

L2{h(tn)} ^ h(tn) - 25 cosh (^to^ - top At) x X h(tn-1) + 52h(tn-2) — 0, где

5 — exp ( -to _s A t ) ,

С использованием отсчетов h(tn ) создадим последовательность to hd (t) — At ^ h (tm )5( t - tm).                     (8)

m — 0

С ее помощью проведем дискретизацию времени в уравнении (4), заменив импульсную характеристику h ( t ) на последовательность (8). После интегрирования для значений решения на временной сетке t_n получим уравнение дискретной свертки

n

X ( t n ) — A t ^ f ( x ( t k ), y ( t k ) ) h ( t n - t k ) + X ( t n ). (9) k — 0

Теперь обе части уравнения (9) подвергнем воздействию разностного оператора L 2 { ° } • При n > 2 это приводит к следующему результату:

L 2 { x ( t n ) } — f ( x ( t n - 1 ), y ( t n - 1 ) ) h (A t )A t •          (10)

Отметим, что в процессе преобразования правой части (10) использованы равенство h (0) — 0, уравнение (7) и аналогичное ему уравнение L 2 { X (t n ) } — 0.

Аналогичным образом, с помощью отсчетов hy(tn) импульсной характеристики hy(t) — k3toc exp (-toct) проводится дискретизация времени во втором уравнении системы (3). Результат дискретизации

y ( t n ) — о y ( t n - 1 ) + k 3 to c x ²( t n )A t •                  (11)

В динамике нелинейных ДВ-систем численный алгоритм вида (10)–(11) становится самостоятельным объектом исследований. Он задает динамическую систему, свойства которой могут существенно отличаться от свойств моделируемого аналогового прототипа.

Введя в рассмотрение частоту дискретизации to d — 2n / A t и пересчитав в ее единицах все остальные частоты (Q _s —to _s / to d , Q d —to d / to d , Q _c — to c / to d ) уравнения движения ДВ-системы для функций дискретного аргумента x [ n ] — — д/2nQ _ск з x ( t_n ), y [ n ] — y ( t_n ) запишем в виде

x [ n ] — a 1 x [ n -1] + a 2 x [ n - 2] +

+ Y ( 1 - y [ n - 1] ) x [ n - 1],                          (12)

y[n] — оy[n - 1] + x2[n] , n — 2,3, ••• и начальным условиям h (10) — h (0) — 0,

k to² 5         I 1 —z-----—

h(t1) — h(At) — . p p = sinh Um^ - top At too - ton                         '

sp

В уравнениях использованы обозначения a 1 — 25 cosh ( 2л^ - Q p ) , a₂ — -5² , y — 2n , k^{p Q p 5} sinhf J Q 2 - Q 2 ,

TQf^Qp       s p)

уМ

5 = exp ( -2nQ _s ) , о = exp ( -2nQ c ) .

Начальное состояние ДВ-системы задается значениями x [0], x [1], y [0] и y [1].

Уравнения (12) содержит четыре независимых параметра: частоты Q _s , Q _p , Q c и коэффициент глубины положительной обратной связи k_p . Впрочем, вместо k_p независимым можно считать параметр у. При различных комбинациях их значений реализуются как регулярные, так и хаотические режимы автоколебаний.

Отметим также, что еще один алгоритм вида (12) для генерации автоколебаний в дискретном времени предложен в работе [9]. Общностью алгоритмов является управление коэффициентом передачи в кольце усилителя и обратной связи (первое из уравнений (12)) с помощью нелинейной инерционной цепи, функционирующей в соответствии со вторым уравнением (12). На основании такой общности ДВ-систему с уравнениями движения (12) будем обозначать как автогенератор с инерционной нелинейностью. Отметим при этом, что коэффициенты перво-

1.5

0.5

в)

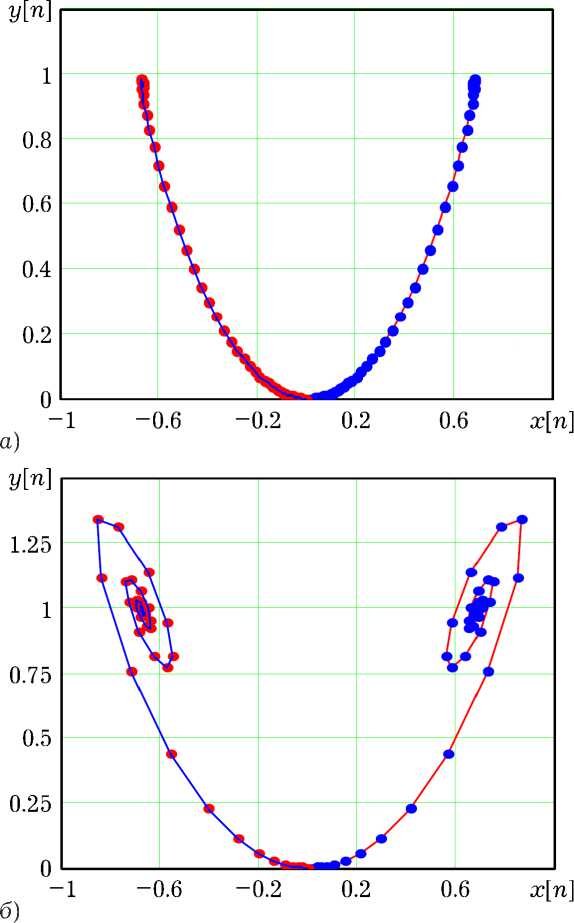
Рис. 5. Траектории ДВ-системы на плоскости ( х , у )

0.9      ;г[п]

-1.5   -0.9    -0.3     0.3

го из уравнений (12) определяются не колебательными процессами, как это имеет место в алгоритме работы [9], а процессами релаксации.

• 3.    Режимы ДВ-генератора с инерционной нелинейностью

Система (12) при у > 0 имеет три состояния равновесия:

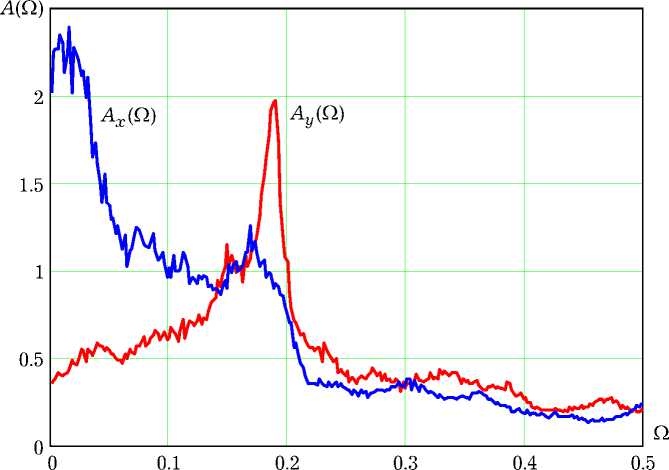
Рис. 6. Усредненные амплитудные спектры процессов x [ n ] и y [ n ]

( ^x 0 , У 0 ) ₀ = ^{( 0,0 )} ,

( ^x 0 , ^y 0 ) 1 = ^ V ⁽¹ - ^{g )(1} - У - 1^{(1 - а} 1 - ^а 2 )),

1 - У 1^{(1 - а} 1 ^{- а} 2 )

( ^x 0 , ^y 0 ) 2 = ^ - V ⁽¹ - ^{о )(1} - У - 1^{(1 - а} 1 - ^а 2 )),

1 - у^-1(1 -« 1 -а 2 )

Об их устойчивости можно судить по величине корней характеристических уравнений линеаризованных систем.

Для состояния ( x 0 , У 0 ) 0 линеаризованная система имеет вид

x [ n ] = а 1 x [ n -1] + а 2 x [ n - 2] + у x [ n - 1],

У [ n ] = o y [ n - 1], n = 2,3,...

Ей соответствуют характеристические уравнения

Z 22 ^- ( ^а 1 ^{+ Y} ) Z 1,2 ^{- а} 2 = ⁰ и Z 3 = ^о .           ⁽¹³⁾

При выполнении условия

0 < у < 1 - а 1 - а₂

все три корня таковы, что Z i | < 1. Следовательно, состояние ( x 0 , У 0 ^ устойчиво.

При у > 1 - а 1 - а 2 в зависимости от начальных условий система (12) переходит в одно из состояний ( x 0 , У 0 ) 1 или ( x 0 , У 0 ) 2 , которые с ростом у сохраняют устойчивость до тех пор, пока модуль одного из корней характеристического уравнения

Z 3 ^- ( о + ^а 1 + У ⁽ 1 ^{- у} 0 ^{- 2} x 0 ) ) Z ² +

+ ( оа 1 + оу(1 - У 0 ) - а 2 ) Z + ста 2 = 0

не превысит единицу. После этого система переходит в автоколебательный режим, образованный переходами между состояниями ( x 0 , У 0 ) 1 и

^{( x} 0 , У 0 V

Граница режима автоколебаний в пространстве параметров системы может быть определе- на путем численного решения уравнения max (| Zi (У, Q s, Q p, Q c |) = 1.

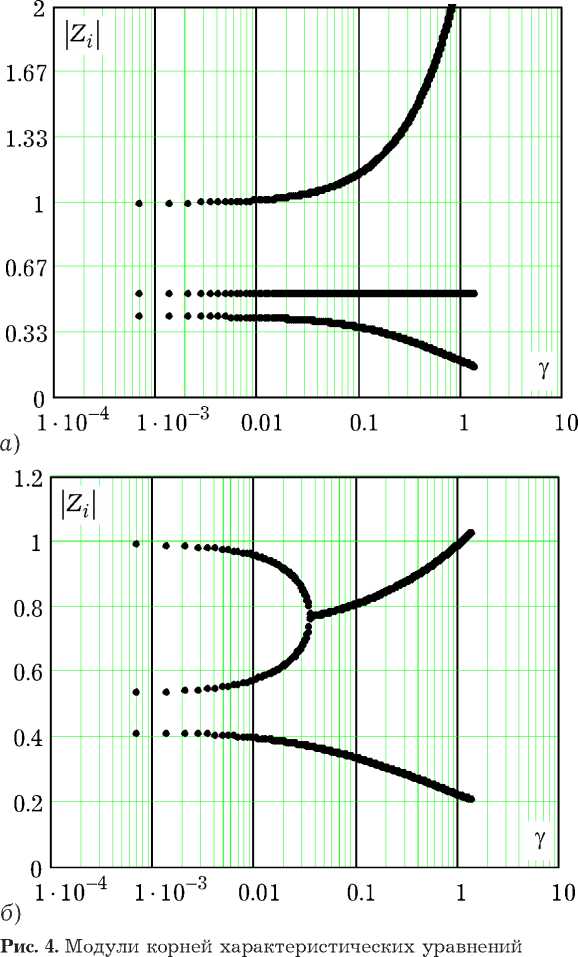
На рис. 4 приведены зависимости модулей корней характеристических уравнений от параметра глубины обратной связи у при фиксированных значениях Q„ = 0.07, Q = 0.01 и Q„ = 0.1. sp  c

Рис. 4, а отвечает корням уравнения (13), а рис. 4, б – уравнения (14).

Для указанных значений параметров Q _s , Q p и Q _c верхняя граница устойчивости состояния ( x 0 , У 0 ) 0 приблизительно соответствует величине у = 2.562 ■ 10 ³, а верхняя граница устойчивости состояний ( x 0 , У 0 ) 1 или ( x 0 , У 0 ) 2 — величине у = 1.032.

Рис. 5 на плоскости ( x [ n ], y [ n ] ) отображает траектории перехода от неустойчивого состояния ( x 0 , У 0 ) 0 в окрестности состояний ( x 0 , У 0 ) 1 и ( x 0 , У 0 )„ . Плоскость ( x [ n ], y [ n ] ) на рис. 5, а ха-²                                     - 3

рактерна для значений 2.562 ■ 10  <у< 0.038, при которых особые точки (x0, У0 )1 и (x0, У0 )2 являются устойчивыми узлами. Траектории на рис. 5, б типичны для 0.038 < у < 1.032, когда особые точки (x0, У0 )1 и (x0, У0 )2 — устойчивые фоку-

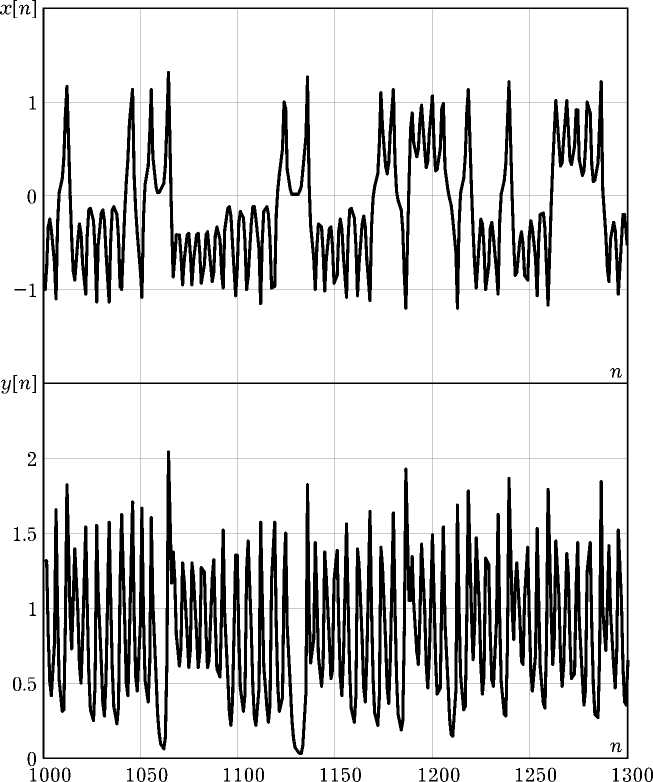
Рис. 7. Отрезки реализаций процессов x [ n ] (вверху) и y [ n ] (внизу)

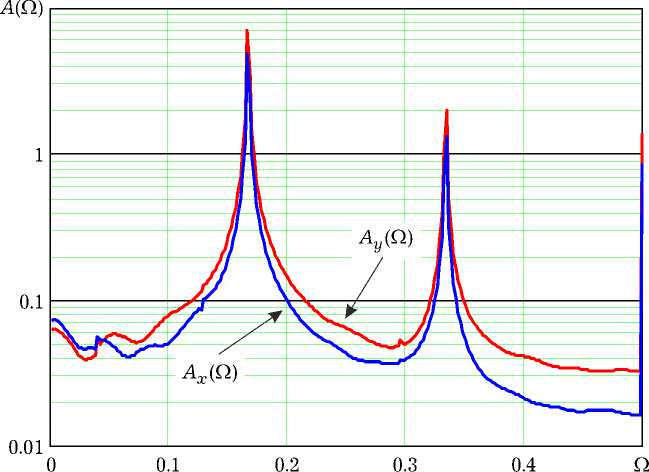
Рис. 8. Амплитудные спектры процессов x [ n ] и y [ n ]

сы. При у > 1.032 в ДВ-системе (12) наблюдаются регулярные автоколебания в окрестности одного из состояний ( x о , Уо ) 1 или ( X q , Уо ) 2 , которые при дальнейшем увеличении у хаотизируются за счет переходов между этими состояниями.

Аттрактор хаотического режима на рис. 5, в формируется при значении у = 1.34. Поскольку сплошной спектр служит одним из эвристических критериев [3] динамического хаоса, рис. 6, на котором приведены усредненные амплитудные спектры A x (Q) и A y (Q) сигналов x [ n ] и y [ n ] (их реализации показаны на рис. 7), подтверждает хаотичность аттрактора. Оценки спектров получены методом Бартлетта с 512-точечным преобразованием Фурье по отрезкам реализаций (см. рис. 7) из 65536 отсчетов. Для сравнения на рис. 8 даны амплитудные спектры регулярных автоколебаний, наблюдаемых при у = 1.07. Из спектра A y (Q) на рисунках удалена постоянная составляющая.