О геометрическом представлении группы вращений правильного тетраэдра
Автор: Скородумов В. Ф., Штепин Д. М.
Журнал: Труды Московского физико-технического института @trudy-mipt
Рубрика: Математика
Статья в выпуске: 2 (58) т.15, 2023 года.
Бесплатный доступ
В работе строится геометрический граф группы А4 (отличный от графа Кэли), исследуется ее геометрическое представление и вычисляется его спектр. Неприводимые компоненты этого спектра - представления А4 вращениями правильного тетраэдра. Фактически дается алгоритм построения многогранника в евклидовом пространстве с заданной группой вращений.
Граф кэли, геометрический граф группы, геометрическое представление конечной группы, выпуклая оболочка графа группы, группы вращений многогранников, неприводимое представление вращениями правильного тетраэдра
Короткий адрес: https://sciup.org/142238158
IDR: 142238158 | УДК: 512.542.1,
Текст научной статьи О геометрическом представлении группы вращений правильного тетраэдра
Пусть G — конечная мультипликативная группа порядка п Пусть М — фиксированный набор образующих G. Назовем словом конечное произведение элементов М и обратных к ним элементов. Хорошо известно [1], что по группе G можно построить связный граф (называемый графом Кэли) так, что:
-
1) элементы группы находятся во взаимно однозначном соответствии с вершинами графа;
-
2) если а С Мид^ = адд, то на графе группы вершины д, и дд связаны ориентированным ребром, ведущим из дд в д,, причем ребра одного «цвета» связаны с одним и тем же образующим, принадлежащим М;
-
3) каждое слово, представляющее элемент группы, можно интерпретировать как путь или некоторую последовательность ориентированных ребер графа, и наоборот;
-
4) умножение двух элементов группы соответствует прохождению на графе пути, составленного из двух последовательных путей;
-
5) любое слово, представляющее нейтральный элемент е, соответствует замкнутому пути на графе;
-
6) расстояние между вершинами а и Ь графа — это длина минимального пути (без учета ориентации ребер) из а в Ь. Максимальное расстояние между вершинами для конечных графов будем называть диаметром графа.
Графы Кэли используются, например, в распределенных компьютерных вычислениях для представления взаимодействия сетей: вершины в этих графах соответствуют обрабатывающим информацию серверам и модулям памяти, а ребра соответствуют линиям связи.
Однако приведенное выше определение графа Кэли группы не совсем удобно ввиду следующих причин. Граф Кэли строится неоднозначно и существенно зависит от выбора набора образующих М. В зависимости от выбора образующих граф группы может иметь разное количество ребер. Также до сих пор не существует алгоритма, позволяющего построить некий «стандартный» граф Кэли группы.
Кроме того, даже при небольшом числе образующих число слов растет экспоненциально в зависимости от длины слова. Например, для группы Томпсона Ғ при четырех образующих и длине слова 14 общее число слов составляет 414 = 268 435 456, среди которых 1 988 452 фактически представляют собой нейтральный элемент е группы Ғ [2]. Таким образом, вычислительные сложности при исследовании графов Кэли возникают даже для групп с небольшим числом образующих. В более сложных задачах возникают такие алгебраические понятия, как «число Бога» (диаметр графа Кэли), «Монстр» (группа порядка 246 • з20 • 59 • 76 • 112 • 132 • 17 • 19 • 23 • 29 • 31 • 41 • 47 • 59 • 71), а задача вычисления минимального пути в графе Кэли, как показано С. Ивеном и О. Голдрейхом, является NP-трудной [3-5].
В работе [6] И. Шульте и Г. И. Уильямс указали метод построения по конечной группе выпуклого абстрактного многогранника, который имеет группу автоморфизмов, изоморфную исходной группе. Однако проблема определения, является ли абстрактный многогранник изоморфным многограннику в евклидовом пространстве, до сих пор является открытой. А автоморфизмы абстрактного многогранника не обязательно являются линейными преобразованиями какого-либо евклидова пространства.
Метод Шульте и Уильямса был обобщен в работе [7] Ж.-П. Дуаньона. В этой работе по конечной группе G строится бинарный многогранник Р(G) у которого каждый комбинаторный автоморфизм индуцирован некоторой изометрией пространства и каждый автоморфизм графа Р (G) является комбинаторным автоморфизмом. Рассматриваемые им изометрии пространства обязательно сохраняют одну из вершин Р (G) неподвижной, следовательно, в его методе группа G не является группой вращений Р (G). Кроме того, углы между вершинами графа и расстояния между ними никак не связаны с внутренними свойствами самой группы G.
Ж.-П. Дуаньон указывает в своей работе важность реализации Р (G) в евклидовом пространстве наименьшей размерности и отмечает, что его алгоритм позволяет построить Р (G) в пространстве размерности не менее чем порядок группы G.
В работах [8, 9] было введено новое понятие геометрического графа группи, в котором существенную роль играют расстояния между элементами группы. Эти расстояния изначально вычисляются с помощью таблиц Кэли, а затем заменяются обычными евклидовыми расстояниями путем вложения графа в евклидово пространство Rm наименьшей возможной размерности. Подчеркнем, что этот метод позволяет реализовать геометрический граф в пространстве R|G|-1 или даже меньшей размерности.
Важным свойством этого определения графа является то, что группа G естественным образом действует на множестве вершин, сопоставляя вектору ж вектор д • ж. В работе [8] доказано, что полученное отображение является линейным оператором в Rm (и в его ком-плексификации Cm) и задает линейное представление группы G. Такие представления на- зываются геометрическими представлениями [8]. Эти представления, согласно теореме Машке [10], являются вполне приводимыми. Отметим, что геометрическое представление всегда имеет размерноств менвшую, чем размерность регулярного представления.
Определение 1. Геометрический граф группы G (геометрическая реализация) — граф группы G на сфере единичного радиус а в евклидовом пространстве Rm наименьшей размерности (обозначим его V). в котором евклидовы расстояния р (назовем их действительными) между элементами группы удовлетворяют соотношению
P(9i,9j )= P(9k,9l ) ^ р (9i,9j )= р (9к,9l ) ^i,j,k,l, (1)
а р — расстояния (назовем их мнимыми) между элементами группы G, вычисленные по формуле
p(9i,9j) = ^2стх(9і,9j ), (2)
Мы будем рассматривать геометрический граф группы G порядка п как набор п различных векторов G = {жі, ж2,..., жп} единичной длины в евклидовом пространстве Rm. В дальнейшем мы будем отождествлять элементы группы G и соответствующие им векторы геометрического графа. Группа G естественным образом действует на множестве {ж1,ж2, ...,жп}. сопоставляя вектору ж і век тор 9 • ж^
Определение 2. Две реализации G 1 и G 2 геометрического графа группы G в Rm назовем эквивалентными, если существует ортогональное преобразование ^ такое, что ^Gi = G 2.
Таким образом, мы ищем геометрический граф группы с точностью до ортогонального преобразования пространства Rm. Геометрический граф является полным, то есть любые две его вершины соединены ребром, причем длины ребер определены однозначно, так как они отражают свойства симметрии самой группы G.
Следующие предложения 1.1-1.5, описывающие основные свойства геометрического графа группы, были доказаны в работе [8].
Предложение 1.1. Для любых элементов ж, у, 9 группы G имеет место равенство р (ж,У)= р (9ж,9У). (3)
Следствие 1. Для любых элементов ж, у, 9 группы G имеют место равенства р ( ж,у ) = р(9ж,^у] я ( ж, у ) = (9ж,9у) (здесь ( ж, у ) — скалярное произведение векторов ж я у евклидова пространства V).
Предложение 1.2. Если жі,ж2,... ,жт — базис евклидова пространства V, состоящий из векторов графа, то 9жі,9ж2,... ,9жт — тоже базис V.
Предложение 1.3. Пусть ж G G и т ж = “i жі , i=1
где ж1,ж2,... ,жт — базис V, состоящий из векторов графа. Тогда
т
9ж = У2 “i 9ж і .
i=1
Далее полагают, что действие 9 G G продолжается с векторов графа по линейности на векторы пространства V.
Следствие 2. Действие д в V является линейным оператором Т(д').
Предложение 1.4. Отображение из G в GL(V ), задаваемое соответствием д ^ Т (д), является линейным представлением группы G.
Определение 3. Представление д ^ Т(д') назовем геометрическим представлением группы G.
Следствие 3. Геометрическое представление любой конечной группы является ортогональным, так как, согласно предложению 1.1, операторы представления сохраняют скалярное произведение в пространстве V. Соответственно, все операторы геометрического представления являются ортогональными матрицами.
Предложение 1.5. Для любого геометрического графа конечной группы G справедливо тождество
^2 cos Z(e, х) = 0, xEG где е - вектор графа. отвечающий нейтральному элементу группы G.
Аналогичная формула справедлива для векторов, отложенных из центра в вершины правильных многогранников.
Заметим, что абстрактная теория групп практически не опирается на геометрию и, вообще говоря, нет однозначно определенного понятия расстояния между элементами группы. Геометрический граф группы позволяет сопоставить элементам группы евклидовы расстояния между ними, углы между элементами группы и многогранник, являющийся выпуклой оболочкой векторов графа. Мы надеемся, что эти новые понятия, соотносимые группе, позволят использовать геометрию евклидовых пространств и многогранников для исследования свойств групп, в том числе и алгебраических.
-
2. Геометрический граф группы А4
Группа А4 — это группа четных подстановок степени 4. она имеет порядок 12.
Упорядочим элементы группы А4 следующим образом:
А = е,В = (2 34), С = (2 4 3), D = (12)(3 4),Ғ = (12 3), F = (12 4), G = (13 2),
Н = (13 4)Д = (13)(2 4), J = (14 2), К = (14 3), L = (14)(2 3).
Для вычисления геометрического графа группы нам потребуется таблица Кэли.
Мнимые расстояния между элементами группы, вычисленные по формуле (2), имеют вид, указанный в табл. 2.
Отметим, что, согласно Предложению 1.1, число троек и единиц в каждой строке и каждом столбце таблицы мнимых расстояний одинаково.
Наша ближайшая цель — вычислить евклидовы расстояния рДдд-; ) между элементами группы А4. Будем считать, что евклидово рас стояние между элементами группы д^ и доопределено однозначно, если определен косинус угла между векторами графа, соответствующими ді и ду Пусть cos /(А, В) = a, a cos Z(A, D) = b. Из определения геометрического графа группы следует, что
' - 1 ^ а< 1,
< -1 ^ b < 1, (4)
_a = b.
Таблица!
Таблица Кэли группы А4
|
* |
А |
В |
С |
D |
Е |
Ғ |
G |
н |
I |
J |
к |
L |
|
А |
А |
В |
с |
D |
Е |
Ғ |
G |
н |
I |
J |
к |
L |
|
В |
В |
с |
А |
G |
I |
н |
J |
L |
К |
D |
Е |
Ғ |
|
С |
С |
А |
В |
J |
К |
L |
D |
Ғ |
Е |
G |
I |
Н |
|
D |
D |
Ғ |
Е |
А |
С |
В |
К |
J |
L |
Н |
G |
I |
|
Е |
Е |
D |
Ғ |
Н |
G |
I |
А |
В |
С |
К |
L |
J |
|
Ғ |
Ғ |
Е |
D |
К |
L |
J |
Н |
I |
G |
А |
С |
В |
|
G |
G |
Н |
I |
в |
А |
С |
Е |
D |
Ғ |
L |
J |
к |
|
Н |
Н |
I |
G |
Е |
Ғ |
D |
L |
К |
J |
В |
А |
с |
|
I |
I |
G |
Н |
L |
J |
К |
В |
С |
А |
Е |
Ғ |
D |
|
J |
J |
L |
К |
С |
В |
А |
I |
G |
Н |
Ғ |
D |
Е |
|
К |
К |
J |
L |
Ғ |
D |
Е |
С |
А |
В |
I |
Н |
G |
|
L |
L |
К |
J |
I |
Н |
G |
Ғ |
Е |
D |
С |
В |
А |
Т а б л и ц а 2
Таблица мнимых расстояний между элементами группы
|
* |
А |
в |
с |
D |
Е |
Ғ |
G |
н |
I |
J |
к |
L |
|
А |
0 |
3 |
3 |
1 |
3 |
3 |
3 |
3 |
1 |
3 |
3 |
1 |
|
В |
3 |
0 |
3 |
3 |
3 |
1 |
1 |
3 |
3 |
3 |
1 |
3 |
|
С |
3 |
3 |
0 |
3 |
1 |
3 |
3 |
1 |
3 |
1 |
3 |
3 |
|
D |
1 |
3 |
3 |
0 |
3 |
3 |
3 |
3 |
1 |
3 |
3 |
1 |
|
Е |
3 |
3 |
1 |
3 |
0 |
3 |
3 |
1 |
3 |
1 |
3 |
3 |
|
Ғ |
3 |
1 |
3 |
3 |
3 |
0 |
1 |
3 |
3 |
3 |
1 |
3 |
|
G |
3 |
1 |
3 |
3 |
3 |
1 |
0 |
3 |
3 |
3 |
1 |
3 |
|
Н |
3 |
3 |
1 |
3 |
1 |
3 |
3 |
0 |
3 |
1 |
3 |
3 |
|
I |
1 |
3 |
3 |
1 |
3 |
3 |
3 |
3 |
0 |
3 |
3 |
1 |
|
J |
3 |
3 |
1 |
3 |
1 |
3 |
3 |
1 |
3 |
0 |
3 |
3 |
|
К |
3 |
1 |
3 |
3 |
3 |
1 |
1 |
3 |
3 |
3 |
0 |
3 |
|
L |
1 |
3 |
3 |
1 |
3 |
3 |
3 |
3 |
1 |
3 |
3 |
0 |
Заметим, что матрица, элементами которой являются косинусы углов между векторами графа, фактически является матрицей Грама:
|
Г = Г( А, D, I, L, Е, С, J, Н, G, К, В, Ғ ) = |
|||||||||||||
|
⎛1 |
a |
a |
a |
b |
b |
b |
b |
b |
b |
b |
b \ |
||
|
a |
1 |
a |
a |
b |
b |
b |
b |
b |
b |
b |
b |
||
|
a |
a |
1 |
a |
b |
b |
b |
b |
b |
b |
b |
b |
||
|
a |
a |
a |
1 |
b |
b |
b |
b |
b |
b |
b |
b |
||
|
b |
b |
b |
b |
1 |
a |
a |
a |
b |
b |
b |
b |
||
|
b |
b |
b |
b |
a |
1 |
a |
a |
b |
b |
b |
b |
. (5) |
|
|
— |
b |
b |
b |
b |
a |
a |
1 |
a |
b |
b |
b |
b |
|
|
b |
b |
b |
b |
a |
a |
a |
1 |
b |
b |
b |
b |
||
|
b |
b |
b |
b |
b |
b |
b |
b |
1 |
a |
a |
a |
||
|
b |
b |
b |
b |
b |
b |
b |
b |
a |
1 |
a |
a |
||
|
b |
b |
b |
b |
b |
b |
b |
b |
a |
a |
1 |
a |
||
|
1b |
b |
b |
b |
b |
b |
b |
b |
a |
a |
a |
1 |
||
По сравнению с табл. 2 векторы графа были переупорядочены с тем, чтобві по главной диагонали матрицы Грама образовались три блока 4 х 4, внутри которых углы между различными векторами совпадают.
Будем искать значения а и Ь, удовлетворяющие системе (4), при которых ранг матрицы Грама Г принимает наименьшее возможное значение (оно и будет равно размерности геометрической реализации графа группы АД.
Теорема 1. Для группи четных подстановок А4 геометрический граф реализуется в евклидовом пространстве V размер пости 9. С точностью до ортогонального преобразования пространства векторы графа имеют координаты:
|
А = (1, |
о , о , |
о , о , о , |
о , о , о , |
|
D = ( — 3 |
2√2 , 3 , |
о , о , о , |
о , о , о , о , |
|
1 = ( — 3 |
√2 - - , 3 |
√6 , 3 , о, |
о , о , о , о , о , |
|
Ь = ( — 3 |
√2 — - , 3 |
, — ^3“, о, |
о , о , о , о , о , |
|
Е = ( 0 , |
о , о , |
1 , о , о , |
о , о , о ) , |
|
с = ( о , |
о , о , |
1 2√2 - 3 , ~, |
о , о , о , о , |
|
7 = ( о , |
о , о , |
1 √2 3 , 3 |
, 1 6 , о , о , о) , |
|
н = ( о , |
о , о , |
1 √2 3 , 3 |
, — f , о , о , о) , |
|
с = ( о , |
о , о , |
о , о , о , |
1 , о , о ) , |
|
к = ( о , |
о , о , |
о , о , о , |
— 3 , V2, о ) , |
|
В = ( о , |
о , о , |
о , о , о , |
_ 1 V I ) 3 , 3 , 3 , |
|
г = ( о , |
о , о , |
о , о , о , |
_ 1 _V6), 3 , 3 , 3 |
Доказательство. Покажем, что в пространстве размерности меньше, чем 9, гео метрический граф группы А4 не реализуется. Вычислим характеристический многочлен матрицы (5):
х ( А ) = ( А + а — 1) 9 ( А — 3 а — 8 Ь — 1)( А — 3 а + 4 Ь — 1) 2 .
Корнями характеристического многочлена являются: (1 — а) — кратности 9, 3а + 8Ь + 1 — кратности 1, 3а — 4Ь + 1 — кратности 2. Матрица (5) является матрицей самосопряженного линейного оператора, поэтому ее ранг равен числу ее ненулевых собственных значений. Понятно, что ранг матрицы (5) будет минимальным, когда а и Ь принимают такие значения, чтобы наибольшее число собственных значений обратилось в ноль. Собственное значение (1 — а) не может равняться нулю, так как тогда cos Z(A, В) = 1. то есть А = В. Приравняем к нулю оставшиеся собственные значения и получим систему из двух уравнений, из которой следует, что а = —1 / 3. Ь = 0.
Если бы граф реализовывался бы в пространстве размерности меньше 9, то это бы означало, что ранг матрицы Грама не превосходит 8, соответственно, эта матрица должна иметь хотя бы 4 нулевых собственных значения. А это противоречит условию а = 1.
Теперь покажем, что эти векторы образуют геометрический граф в пространстве раз- мерности 9. Действительно, матрица Грама для этих векторов имеет вид
|
1 |
1 1 — 3 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
1 - |
1 |
-- 3 |
- |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
— о |
1 — о |
1 |
— 3 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
- 3 |
-3 |
1 - 3 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
⎜0 |
0 |
0 |
0 |
1 |
1 ■ ■ — 3 |
1 -п |
1 |
0 |
0 |
0 |
0 |
|
|
0 |
0 |
0 |
0 |
1 - |
1 |
- — 3 |
- |
0 |
0 |
0 |
0 |
. (6) |
|
⎜0 |
0 |
0 |
0 |
-- о |
1 |
1 |
■ ■ — 3 |
0 |
0 |
0 |
0 |
|
|
⎜0 |
0 |
0 |
0 |
- — 3 |
- — 3 |
1 - — 3 |
1 |
0 |
0 |
0 |
0 |
|
|
⎜0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 ■ ■ — 3 |
1 ---77 |
1 -- 77 |
|
|
⎜0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 - |
1 |
- |
—— — 3 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
- — 3 |
1 - — 3 |
-- 3 |
1 |
|
Заметим, что в матрице Грама фактически указаны косинусы углов между векторами (т.к. все векторы графа имеют единичную длину). Эти косинусы совпадают для тех и только тех пар векторов, для которых совпадают мнимые расстояния в табл. 2. Так, мнимому расстоянию 1 в матрице Грама соответствует угол, косинус которого равен а = -1/3, а мнимому расстоянию 3 в матрице Грама соответствует угол, косинус которого равен b = 0.
Найдем теперь координаты векторов геометрического графа. Из явного вида матрицы Грама (6) имеем
V = L(A, D, I, L) ф L(E, С, J, Н ) ф L(G, К, В, F ).
Поэтому, фактически, граф разбивается в прямую сумму трех графов, отвечающих четверкам векторов (A, D,I, L) (E,C,J,H ) и (G,K,B,F ). Косинусы углов между различными векторами в каждой четверке равны -1/3, что отвечает углам между радиус-векторами вершин правильного тетраэдра в R3. Стандартное задание координат этих радиус-векторов
A = (1,0,0). D = Ф1, 2Д Д . I = (- 1,-£<). L = Ф 1,-£ 33 3 3 3 3 3
-
Теорема, доказана.
Замечание. Как следует из теоремы 1, геометрический граф группы вращений правильного тетраэдра, реализуется в пространстве, размерности строго меньшей, чем порядок группы. На самом деле этот факт справедлив для любой конечной группы, что мы докажем в следующей теореме.
Теорема 2. Размерность геометрического графа любой конечной группы (и размерность ее геометрического представления) удовлетворяют неравенству.
dim V < |G|.
Доказательство. Матрица Грама Г, как отмечалось выше, состоит из косинусов углов между векторами графа. Поскольку эта. матрица, симметрична, она. является матрицей самосопряженного линейного оператора. Согласно основной теореме о самосопряженных линейных операторах, существует ортонормированный базис, в котором этот оператор принимает диагональный вид. Тогда, ранг матрицы равен числу ненулевых собственных значений (с учетом их кратности).
Утверждение теоремы равносильно тому, что гкГ < |G|. Для этого покажем, что вектор (1,1,..., 1)т является собственным вектором для Г с собственным значением 0.
В г-й строке матрицы Г стоят числа cos/(жі,ж), г де ж пробегает группу G. Заметим, что
У^ cos Z(xt , х) = У2( ж і ,ж ) = (по предложению 1.1) = seG seG
= 52(ж— • х ,х — • ж ) = у2( е,ж — • х). (7) seG seG
Обозначим х- 1 • х через у. Очевидно, что если х пробегает группу G, то и у пробегает группу G . Тогда по предложению 1.5 получаем
У2 cos /(хдх) = ^(е,х- 1 • х) = ^(е,у) = ^ cos Z(e,y) = 0. seG seG yeG yeG
Итак, оператор Г аннулирует вектор (1,1,..., 1)т.
Теорема доказана.
Заметим, что оценка dim V ^ |G| — 1 для произвольной конечной группы не улучшаема. Действительно, для геометрического графа циклической группы Ср, г де р — простое, выполняется dim V = р — 1 [8].
-
3. Неприводимые представления группы А4
Известно, что неприводимые представления конечных групп с точностью до изоморфиз ма определяются их характерами. Характеры неприводимых представлений хорошо извест
-
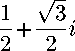
ны [10,11]. Они перечислены в следующей табл. 3. Здесь введено обозначение: ш = — первообразный корень третьей степени из единицы.
Т а б л и ц а 3
Характеры неприводимых комплексных представлений группы А4
|
А 4 |
А = е |
D = (12)(34), I = (13)(24), L = (14)(23) |
С = (243), Е = (123), Н = (134), J = (142) |
В = (234), F = (124), G = (132), К = (143) |
|
Т |
1 |
1 |
1 |
1 |
|
Т 2 |
1 |
1 |
ш |
0 |
|
Т з |
1 |
1 |
ш |
ш |
|
Т 4 |
3 |
-1 |
0 |
0 |
Отметим, что А4 обладает единственным неодномерным неприводимым представлением Т4 размерности 3. Это представление группы вращениями правильного тетраэдра. Построим явную реализацию этого представления в R3.
Вершины тетраэдра выберем в виде точек на единичной сфере:
а (1 , 0, 0),d — 1, 2Z,0 ., — 1, —2?, 2 _L — 1, — V2, — V6 .
( , , ), 3, 3 , , 3, 3 , 3 , 3, 3 , 3
Заметим, что векторы А — L геометрического графа, построенного в теореме 1, имеют именно такие координаты при сужении на R3.
Пусть
(— 1
T 4 (D) = 2V2
2V2
3 0
—1
.
Легко увидеть, что этот оператор переводит векторы A,D,I,T соответственно в D,A,T,I. Следовательно, это поворот тетраэдра на угол тг вокруг прямой, соединяющей середины ребер [A, D] и [I, Т]. Такой же геометрический смысл имеют и операторы Т4(I ) и Т4(Т). Пусть
Т4(С ) =
|
⎛ |
1 — |
\2 — |
У6 \ |
|
2^2 |
3 1 |
3_ у3 |
|
|
3 |
— 6 |
"6" |
|
|
⎝ |
V3 |
1 |
|
|
0 |
2 |
2 / |
.
Вектор [О, Т], г де О — начало координат, является собственным вектором для этого оператора с собственным значением 1. Да лее, Т4(С )(A) = D, Т4(С )(D) = I, Т4(С )(I ) = A. п 2 г
Следовательно, этот оператор является оператором поворота тетраэдра на угол — вокруг оси [О, Т]. Аналогичный геометрический смысл имеют все операторы от элементов класса сопряженности {С, Е, Н, J}.
Элементы четвертого класса {В, G,K,F} являются обратными к соответствующим эле-2г ментам третьего класса, поэтому они задают вращения на угол —— вокруг тех же осей.
Очевидно, что других вращений, переводящих правильный тетраэдр в себя, не существует.
Оператор Т4(D) — самосопряженный, следовательно, по основной теореме о самосопряженных операторах приводится в некотором ортонормированном базисе к диагональному виду. Такой базис называют каноническим базисом самосопряженного оператора.
В данном случае таким каноническим базисом является е! =
3 Уе "3" \ 0 /
(_ ^3 \ 3 V6
е
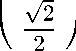
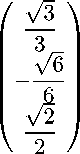
В этом базисе образующие элементы D
и С группы A4 задаются следующими операторами:
1 0 0 0 0 1
Т 4 ( D ) (e‘) = 0 - 1 0 , Т 4 ( С)и = 1 0 0 .
00 - 1 010
Приведем матрицы остальных операторов базисе:
представления Т4 в найденном каноническом
- 1
Т4(A) = Е (единичная матрица), Т4(I)(в‘) =0
Третий класс:
/ 0 0 1\ / 00
Т 4 ( Е )и = - 1 0 0 , Т 4 ( Н ) ( в‘ ) = - 10
0 -1001
Четвертый класс:
0 0
-10 , Т4(Т)(в‘) =0
-1 00
0 , Т. 2)(в‘) = 10
- 1
- 1
Т 4 ( В ) ( в‘ ) = 0 0 1
Т4 (F )(в‘) = 0 0 -1
-1 00
/0 -10
Т4(G)(в‘) = I 0 0-1
100 /
Т4(К)(в‘) = I 0 011
-1 00
Легко проверить, что перечисленные операторы удовлетворяют условию гомоморфизма, следовательно, задают представление Т4.
-
4. Разложение геометрического представления группы М4 в прямую сумму неприводимых
Левое умножение на элемент D в группе А4 задает следующее действие на элементах группы:
D :
/ А D I
V D А L
LY Л
Е С J СЕН
Н J
),D:(
G К В F К G F В
)•
Поскольку элементам группы соответствуют векторы геометрического графа группы А4, то мы можем получить явный вид оператора Tgeom(D) в исходном базисе пространства V :
|
⎛ - 1 3 |
2√2 3 |
0 |
0 |
0 |
0 |
0 |
0 |
0 ^ |
|
|
22 3 |
1 3 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
0 |
0 |
- 1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
0 |
0 |
0 |
1 - — 3 |
2√2 3 |
0 |
0 |
0 |
0 |
|
|
Tgeo m(D) — |
0 |
0 |
0 |
2√2 3 |
1 3 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
- 1 |
0 |
0 |
0 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
1 - — 3 |
2√2 3 |
0 |
|
|
0 0 |
0 0 |
0 0 |
0 0 |
0 0 |
0 0 |
2 √ 2 3 0 |
1 3 0 |
0 - 1 |
|
Аналогично найдем матрицу оператора Tgeoт(С). Левое умножение на элемент С в группе А4 задает следующее действие на элементах группы:
С :
А D
С J
I L
Е Н
УЦ
Е С J Н К В G F
) ,С:(
G D
К В
I А
F
•
Отсюда явный вид оператора в исходном базисе V:
|
0 |
0 |
0 |
0 |
0 |
0 |
1 - — 3 |
2 - - 3 |
6 3 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
22 3 |
1 - — 6 |
3 6 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
3 2 |
1 2 |
|
|
Tgeo т(С) — |
1 ■ ■ — 3 22 3 |
√2 — - 3 1 - — 6 |
√6 3 3 6 |
0 0 |
0 0 |
0 0 |
0 0 |
0 0 |
0 0 |
|
0 |
3 2 |
1 2 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
0 0 0 |
0 0 0 |
0 0 0 |
1 1 ----------------- 3 22 3 0 |
√2 ■ ----------------------- 3 1 ■ ■ --------- 6 3 2 |
√6 3 3 6 1 2 |
0 0 0 |
0 0 0 |
0 0 0 |
Так как D и С — образующие элементы группы А4, то мы в состоянии теперь найти характер геометрического представления Tgeom.
Кратность mt вхождения неприводимого представления Т в представление Tgeom вычисляется по формуле [10]:
mi — ( Xi, Age от) •
По этой формуле находим: mi — m2 — m3 — 0 и m4 — 3. Следовательно, мы приходим к следующей теореме.
Т а б л и ц а 4
Характер геометрического представления группы А4
|
А 4 |
А = 6 |
D = (12)(34), I = (13)(24), L = (14)(2 3) |
С = (243), Е = (123), Н = (134), J = (142) |
В = (234), Ғ = (124), G = (132), К = (14 3) |
|
Т 1 |
1 |
1 |
1 |
1 |
|
Т 2 |
1 |
1 |
ш |
Ш |
|
Т з |
1 |
1 |
ш |
ш |
|
Т 4 |
3 |
-1 |
0 |
0 |
|
Тдеот |
9 |
-3 |
0 |
0 |
Теорема 3. Геометрическое представление группы А 4 разлагается в прямую сумму неприводимых:
Т„еоm = Т4 Ф Т4 Ф Т4 = ЗТ4 .
Касисдая неприводимая компонента изоморфна представлению группы А 4 вращениями правильного тетраэдра.
Доказательство. Оператор Т§еот(2Э) является самосопряженным. Поэтому в некотором ортонормированном базисе пространства V он приводится к диагональному виду.
Стандартными вычислениями мы можем найти канонический ортонормированный базис, в котором Тбео m(-D) диагонализируется:
⎛ √ 1 3 ⎞ 2
⎜ 3 ⎟ 0
⎜ 3 ⎟ √2
⎛-√ 1 3 ⎞ 2
⎛ 1 3√ ⎞ 2
-
,6 2
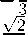
-
,f 1
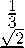
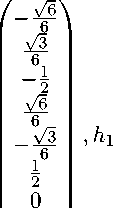
-
-
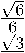
,/ 2
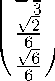
⎛ √2 ⎞ 3 2
√2
--- --
⎜ √2⎟
■ ■ 11
⎜- 61
—— --
-
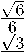
⎛ √2 ⎞ 6 1
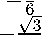
, ^ 2
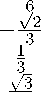
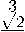
-
1/6
, ^ 3
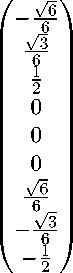
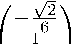
-
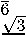
-
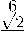
-
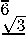
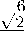
-
По сравнению с базисом 6’1,62,63 (7) координаты векторов 61,62,63 отличаются множителем ^=. Это объясняется тем, что длины векторов остаются неизменными (так как базисы ортонормированные), но мы уже находимся в пространстве размерности 9. Векторы /1,/2,/з получены следуют,им образом: вектор fi — единичный собственный вектор для оператора Т„е( )Ш( Р) с собственным значением 1. ортогопалыіый векторам 61,62, 63. далее
/2 = Tgeom(C')(/1), /з = Tgeom(C')(/2). Наконец, Һ1 — единичный собственный вектор для оператора Т§ео m (D) с собственным значением 1, ортогональный векторам е1, е2, ез, /1, /2, /3. Далее. ^2 = Tgec)ш(С')(^T) ^3 = Tge<:>іп(С'Х^)
В построенном ортонормированном базисе операторві геометрического представления упрощаются. Мы здесв дадим толвко операторві на образующих элементах группы:
|
1 0 |
0 - 1 |
0 0 |
0 0 |
0 0 |
0 0 |
0 0 |
0 0 |
0 0 ⎟ |
|
|
0 |
0 |
- 1 |
0 |
0 |
0 |
0 |
0 |
0 ⎟ |
|
|
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 ⎟ |
|
|
Tgeo m(D)(e,f,h) = |
0 0 |
0 0 |
0 0 |
0 0 |
- 1 0 |
0 - 1 |
0 0 |
0 0 |
0 ⎟ 0 ⎟ |
|
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
- 1 |
0⎟ |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
- 1 |
|
|
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 ⎟⎟ |
|
|
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
|
|
Tgeom(C ^e,/,^ = |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 ⎟⎟ |
|
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1⎟ |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0⎟ |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
|
Мы специально выделили по главной диагонали блоки 3 х 3 с тем, чтобы показать, что геометрическое представление Tgeom раскладывается в прямую сумму трех трехмерных подпредставлений. Каждое из них изоморфно представлению группы А4 вращениями правильного тетраэдра. Теорема доказана.
-
5. Заключение
В данной работе мы построили геометрический граф группы А4, для нее dim V = 9. Здесь же мы построили геометрическое представление группы А4 и разложили его в прямую сумму неприводимых. Это разложение имеет вид Tgeom = Т4 ф Т4 ф Т4, где Т4 - представление группы А4 обычными вращениями правильного тетраэдра. Оно же является неприводимым представлением А4 наибольшей размерности, и явное построение таких реализаций - наиболее сложная задача теории представлений конечных групп.
С точностью до ортогональных вращений V найдены векторы геометрического графа, который также может быть представлен в виде прямой суммы трех изоморфных подграфов:
G = G1 ф G2 ф G3 , (9)
где (Gi, Gj ) = 0 пр и г = ф
Вершины каждого из этих графов совпадают с вершинами правильного тетраэдра, и операторы геометрического представления в каждом блоке 3 х 3 задают его вращения. Фактически по группе А4 мы построили многогранник, для которого эта группа является его группой вращений.
Легко проверить, что граф Gi является геометрическим графом нормальной подгруппы в А4, состоящей из элементов {А, D, I, L} Эта подгруппа, как известно, изоморфна группе Клейна V4.
Вероятно, само существование ортогонального разложения (9) в сумму трех изоморфных подграфов связано с наличием в группе А4 нормальной подгруппы V4 индекса 3.
Согласно следствию из предложения 1.4, предложенный алгоритм построения геометрического графа позволяет для произвольной группы G построить такой многогранник Р (G), что G изоморфна некоторой подгруппе группы вращений Р (G). В качестве такого многогранника достаточно взять выпуклую оболочку векторов геометрического графа. Действие операторов Т(д') на многограннике Р (G) нетривиально при д = е. Следовательно, ядро представления д н- Т(д') тривиально.
В отличие от метода Шульте и Уильямса [6], многогранник Р (G), сопоставляемый в нашей работе конечной группе G, заведомо реализуется в евклидовом пространстве, а по сравнению с многогранником Ж.-П. Дуаньона, еще и в пространстве меньшей размерности. Как следует из теоремы 2, размерность Р (G) не превосходит |G| — 1.
В заключение мы хотели бы выразить благодарность рецензенту А.М. Райгородскому, обратившему наше внимание на работы [6,7] и побудившему нас доказать новую теорему 2.
Список литературы О геометрическом представлении группы вращений правильного тетраэдра
- Гроссман И., Магнус В. Группы и их графы. Москва: Мир, 1971.
- Arzhantseva G. [et al.]. Geometric group theory // Proceedings of the Geneva and Barcelona Conferences. Birkhauser. 2007. 24 c.
- Even S., Goldreich O. The Minimum Length Generator Sequence is NP-Hard // Journal of Algorithms. 1981. N 2. P. 311–313.
- Овчаренко А.Ю. О целочисленных графах Кэли для 𝐴𝑛 // Международная научная конференция «Актуальные проблемы прикладной математики и физики», Нальчик. Терскол. 2017. 160 c.
- Griess R.L., Meierfrankenfeld U., Segev Y. A uniqueness proof for the Monster // Annals of Mathematics. Second Series. 1989. V. 130, N 3. P. 567–602.
- Schulte E.L., Williams G.I. Polytopes with Preassigned Automorphism Groups // Discrete Comput. Geom. 2015. V. 54. P. 444–458.
- Doignon J.-P. Any Finite Group is the Group of Some Binary, Convex Polytope // Discrete Comput. Geom. 2018. V. 59. P. 451–460.
- Штепин В.В., Беликова В.А. О геометрических представлениях циклических групп // Национальная академия наук Украины. Труды ИПММ. 2010. T. 20. C. 196–205.
- Штепин В.В., Фрасинич В.А.О геометрическом представлении циклической группы 𝐶8 // Национальная академия наук Украины. Труды ИПММ. 2013. T. 27. C. 250–257.
- Винберг Э. Б. Линейные представления групп. Москва: Наука, 1985.
- Зиза К.Н., Штепин В.В. Геометрические реализации неприводимых представлений групп вращений правильных многогранников в трехмерном пространстве // Труды МФТИ. 2016. Т. 8, N 4. С. 18–34.


