О характеризации корневых множеств одного весового класса аналитических в круге функций
Автор: Шамоян Файзо Агитович, Родикова Евгения Геннадьевна
Журнал: Владикавказский математический журнал @vmj-ru
Статья в выпуске: 3 т.16, 2014 года.
Бесплатный доступ
В работе получено полное описание корневых множеств аналитических в круге функций, допускающих рост вблизи заданного конечного множества точек граничной окружности.
Аналитическая функция, единичный круг, множество нулей аналитической функции
Короткий адрес: https://sciup.org/14318471
IDR: 14318471
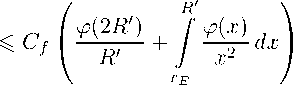
Список литературы О характеризации корневых множеств одного весового класса аналитических в круге функций
- Джрбашян M. M. К проблеме представимости аналитических функций//Сообщ. Института математики и механики АН Арм. ССР.-1948.-№ 2.-C. 3-40.
- Shapiro H. S., Shields A. L. On the zeros of functions with finite Dirichlet integral and some related function spaces//Math. Z.-1962.-№ 80.-C. 217-229.
- Seip K. Interpolating and sampling in spaces of analytic functions.-Providence (R.I.): Amer. Math. Soc., 2004.-183 p.
- Djrbashian A. E., Shamoyan F. A. Topics in the Theory of $A^p_{\alpha$ Spaces.-Leipzig: Teubner-Texte zur Math., 1988.-105 р.
- Шамоян Ф. А. Факторизационная теорема М. М. Джрбашяна и характеризация нулей аналитических функций с мажорантой конечного роста//Изв. АН Арм. ССР. Сер. Математика.-1978.-Т. 13, № 5-6.-C. 405-422.
- Шамоян Ф. А. О нулях аналитических в круге функций, растущих вблизи его границы//Изв. АН Арм. ССР. Сер. Математика-1983.-Т. 18, № 1.-C. 215-228.
- Borichev A., Golinskii L., Kupin S. A Blaschke-type condition and its application to complex Jacobi matrices//Bulletin of the London Mathematical Society.-2009.-Vol. 41.-P. 117-123.
- Golinskii L., Kupin S. A Blaschke-type condition for analytic functions on finitely connected domains. Applications to complex perturbations of a finite-band selfadjoint operator//J. Math. Anal. Appl.-2012.-Vol. 389, № 2.-P. 705-712.
- Favorov S., Golinskii L. Blaschke-Type Conditions for Analytic and Subharmonic Functions in the Unit Disk: Local Analogs and Inverse Problems//Computational Methods and Func. Theory.-2012.-Vol. 12.-P. 151-166.
- Favorov S., Golinskii L. Blaschke-type conditions in unbounded domains, generalized convexity and applications in perturbation theory.-arXiv:1204.4283.
- Favorov S., Radchenko L. On Analytic and Subharmonic Functions in Unit Disc Growing Near a Part of the Boundary//Zh. Mat. Fiz. Anal. Geom.-2013.-Vol. 9, № 3.-P. 304-315.
- Shamoyan F. A. On some properties of zero sets of analytic functions with given majorant//Theory functions and applications. Collections of works dedicates to the memory of M. M. Djrbashian.-Yerevan: Luys Publishing House, 1995.-P. 169-172.
- Шамоян Ф. А. О нулях аналитических в круге функций с заданной мажорантой вблизи его границы//Матем. заметки.-2009.-Vol. 85, № 2.-C. 300-312.
- Hayman W. K., Korenblum B. A critical growth rate for functions regular in a disk//Michigan Math. J.-1980.-Vol. 27.-P. 21-30.
- Быков С. В. Факторизационные представления и свойства корневых множеств весовых классов аналитических функций: Дисс.\ldots канд. физ.-мат. наук.-Брянск: БГУ, 2010.-130 с.
- Титчмарш Е. Теория функций.-М.: Наука, 1980.-480 с.
Статья научная
