О категории MRR-групп над кольцом R

• 1.    Основные определения

Пусть R - произвольное ассоциативное кольцо с единицей 1. В работе А. Г. Мясникова. и В. Н. Ремесленникова [1] была, введена, новая категория степенных R-групп MR-группы) как естественное обобщение на. некоммутативный случай понятия R-модуля.

Напомним основные определение, следуя статьям [1, 2].

Пусть Lgr = (-, ^-1 ,e) - групповой язык (сигнатура), гш бинарная операция умножения. ^-1 — унарная операция обрашення элементов группы, e — константный символ для единицы группы.

Обогатим группой язык Lgr до ж ;ыка Lgr = Lgr ^{f_a(g) : а Е R}. г до f_a(g) - унарная алгебраическая операция.

Определение 1. Множество G будем называть линдановой В-грунной, если на нем определены операции -. ^-1. e . {fa(g) : а Е R} и выполнены аксиомы:

• 1)    аксиомы группы;

• 2)    для всех g,h Е Он всех элементов а,в Е R выполняются равенства

g1 = g, g0 = 1, ea = e;Ш ga+e = ga • ge, gae = (ga)e;(2)

(h-1 gh)a = h-1 ga h.(3)

При записи аксиом мы используем следующее соглашение: для краткости f_a (g) будем записывать в виде g^a. g Е G. а Е R.

Обозначим через Lr категорию всех линдоновых R-групп. Так как аксиомы выше являются универсальными аксиомами языка Lgr, то Lr является многообразием алгебраических систем языка Lgr и, следовательно, из общих теорем универсальной алгебры © следует, что можно говорить о многообразии R-групп, об R-гомоморфизмах, R-изоморфизмах, о свободных R-группах и так далее.

ОПРЕДЕЛЕНИЕ 2. Пусть G, H G Lr. Тогда г<шоморфпзм у : G ^ H называется R. гомоморфизмом. если (g^aД = (g^)^a для лтобых g G G. a G R.

Существуют абелевы линдоновы R-группы, не являющиеся R-модулями (см. [3], где подробно исследована, структура, свободной абелевой R-группы). В работе [1] А. Г. Мясников и В. Н. Ремесленников добавили к аксиомам Линдона, дополнительную аксиому (квазитождество):

(MR)         (V g,h G G) (a G R) [g, h] = e =^ (gh)^a = g^ah^a.          (4)

Определение 3. Группу G будем называть MR-группой, если на G определена операция g^a для всех g G G и при этом выполнены аксиомы (1)-(4).

Обозначим через MR класс всех степенных R-групп с аксиомами (1)-(4). Ясно, что этот класс является квазимногообразием в языке /._ и в нем снова есть понятие свободной MR-группы, MR-гомоморфизма и так далее, и, кроме того, выполнено свойство: каждая абелева. MR-группа является R-модулем и наоборот.

Большинство естественных примеров степенных R-групп лежат в классе M_R:

• 1)    любая группа, является Z-группой:

• 2)    делимая абелева, группа, является Q-группой:

• 3)    группа, периода, n являстоя Z/nZ-группой:

• 4)    модуль над кольцом R является абелевой MR-группой;

• 5)    произвольная про-p-группа, является Zp-группой над кольцом полых р-адпнескпх чисел Z_p.

• 6)    произвольная нильпотентная степенная R-группа над биномиальным кольцом R ^холлова R-группа), введенная Ф. Холлом в [4], является MR-группой.

Нильпотентные группы. Пусть с > 1 — натуральное число. Обозначим через N _c,_R категорию нильпотентных R-групп ступени нильпотентности с из класса L_R, т. е. всех R-групп. в которых для любых x!,...,x_c+1 выполняете!i тождество [х1 , ...,x_c+1] = 1, а через N0 _R - категорию иильпотсштиых R-групп ступени с. в которых выполняется аксиома. (MR). Структура R-групп без аксиомы (MR) очень сложна, поэтому в большинстве работ изучаются только R-группы со свойством (MR). Далее, в статье мы будем рассматривать только R-группы с этой аксиомой.

• 1.2. Холлоны нильпотентные R-группы [4]. Для того чтобы ввести это понятие, нам необходимо ограничить класс рассматриваемых колец.

Определение 4. Кольцо R называется биномиальным кольцом, если R — область целостности, содержащая Z в качестве подкольца, п с каждым элементом a G R включает все биномиальные коэффициенты Ca = ММ__Д_, n g N.

Примерами биномиальных колец являются: любое поле нулевой характеристики, кольцо многочленов над таким полем и кольцо целых чисел.

Определение 5. Нильпотентная группа G ступени нильпотентности с называется R-группой (здесь R-биномиальное кольцо), если для любого a G R их G G единственным образом определен элемент x^a G G и для всех элементов группы G и кольца R выполнены следующие аксиомы (х. у. х1,... ,x_n G G. a, в G R):

• 1)    х¹ = х. x^a+e = x^ax^e. х^ав = (x^a)^e:

• 2)    (y^-1xy)^a = y^-1x^ay.

• 3)    Ха • • • хП = (х_а • • • xn)^aT2(X)C^a • • • Tc(X)C^a, г де X = {x1,..., xn}, т_к (X) — k-e слово Петреску.

• 2.    Тензорное пополнение

Напомним, что для любого натурального к рекурсивно определяется k-e слово Петреску формулой хк • •• хП = T1(X)CkT2(X)Ck • • • Tk-1(X)Ck-1 Tk(X)Ck в свободной группе F с порождающими х1,... ,xn. В частности.

T1(X)= Х1,...,Хп, T2(X) =    .     . [xi,Xj] mod Y3(F), i>j, i,j=1

где Y3 (F ) - третий член нижнего цантрального ряда, группы F. Обозначим категорию холловых R-групп через HNc,_R.

Покажем, что структура групп из Nc,_R очень сильно отличается от структуры холловых R-групп из класса HNc,_R. Для этого приведем структуру свободной R-группы в многообразии HNc,_R, следуя работе [5]. Мы ограничимся рассмотрением двух биномиальных колет; R = Q[t], R = Q(t). Обозначим через G0 евободнуто 2-ступепио нильпотентную R-группу с порождающими х и у. Хорошо известно, что мальцевская база этой группы состоит из трех элементов х, у, [у, х]. Общий вид элемента g G G0 следующий: g = x^Y у⁵ [у,х]Д y,8,e G R. В частности, в эк>й группе коммутант G0 является свободным R-модулем ранга 1 с порождающим [у,х]. Если теперь G — свободная R-группа в многообразии N0,_r, то в работе [5] показано, что G0 является свободным R-модулем бесконечного ранга, и найдена, база, этого модуля.

Систематическое изучение MR-групп начато в работах [5]-[11]. Отметим, кстати, что результаты этих работ оказались весьма, полезны при решении известных проблем Тарского. Настоящая статья посвящена, изучению частичных степенных MR-групп, которые изоморфно вкладываются в свое тензорное пополнение над кольцом R. Ключом к ее пониманию служит понятие тензорного пополнения, введенное в [1]. Как следствие, получено описание свободных MR-групп и свободных MR-произведений на. языке групповых конструкций.

Здесь, следуя [1], вводится основная операция в классе степенных MR-групп. Она. естественно обобщает на. некоммутативный случай понятие расширения кольца, скаляров для модулей.

Определение С. Пусть G - MR-группа. ц : R ^ S - гомоморфизм колец. Тогда MS-группа. GS называется тепзорпнм М ^-пополнением ^-группы G. если GS удовлетворяет следующему универсальному свойству:

• 1)    существует R-гомоморфпзм А : G ^ G^S такой. что A(G) MS-порождаст GS. т. е. h^A(G)is = GS      ,                 ,                ,

• 2)    для любой MS-группы H и любого R-гомоморфизма ^ : G ^ H, согласованного с ц (т. е. такого, что (g^a)^ = (g^)^^(a)). суще(/твует 5-гомомор<1>изм ^ : GS ^ H. делающий коммутативной следующую диаграмму:

G -^GS ф /       (N = д)-

~ ^ф

В [1] доказано, что для любой MR-группы G и любого гомоморфизма ц : R ^ S тензорное пополнение G^S всегда существует и оно единственно с точностью до изоморфизма. Там же показано, что если G — абелева MR-группа, то GS = G 0 S — тензорное R

GS

Операция тензорного пополнения перестановочна с операциями прямого произведения и взятия прямого предела и, вообще говоря, не перестановочна с операциями декартова произведения и взятия обратного предела [7]. Перестановочность тензорного пополнения с прямыми пределами позволяет многие вопросы о пополнениях сводить к случаю конечно порожденной группы. Действительно, пусть {Gi (i Е I );nj} - прямой спектр группы G. составленный из конечно порожденных групп Gi. Тогда G = lim    Gi

^-→t→I и G^S = lim    GS.

v t^i

Построение тензорного пополнения данной группы удобно вести по шагам, постепенно «доопределяя степени». Это приводит к понятию частичной MR-группы. Также к частичным MR-группам приводят некоторые групповые операции над MR-группами. Пусть R - кольцо. G - группа.

Определение 7. Группу G будем называть частичной МП-грунной, если возведение в степень определено для некоторых пар (g,a) но не обязательно для всех пар: причем, если определена одна часть равенства в аксиомах (1)—(4), то определена и другая часть, и для них выполняются аксиомы (1)-(4) в определении MR-группы.

Класс частичных MR-групп будем обозначать через PR. Например, если R - подкольцо кольца S, тогда любая MR-группа является частичной MS-группой.

На протяжении всей статьи будем предполагать, что кольцо R в качестве подкольца содержит кольцо целых чисел Z. Пусть G - частичная MR-группа. т. е. G Е Рц.

Определение 8. Будем говорить, что группа G является точной относительно кольца R. если гомоморфизм А : G ^ G является вложением.

Определение 9. Будем говорить, что группа G является точной, если она является точной относительно любого кольца, содержащего Z.

Пусть R- кольцо. Р⁰ - категория частичных MR-rрупп. По определению группа G из Рц принадлежит Р0. если выполнены следующие условия:

• 1)    для любой максимальной абелевой подгруппы M из G и любого x Е M пересечение M n M^x = e:

• 2)    канонический гомоморфизм j : M ^ M 0R является вложением.

• 3.    Свободные произведения MR-групп

R

Сформулируем основную теорему.

Теорема 1 [9]. Пусть Z — подкольцо кольца R п группа G Е Р 0. при чем в G и R+ (аддитивная группа кольца. R) пет элементов порядка 2. Тогда группа G^R точна, т. е. гомоморфизм А : G ^ G^R является вложением.

При доказательстве этой теоремы используется способ построения тензорного пополнения, основанный на конструкции свободного произведения групп с объединенной подгруппой и техника комбинаторной теории групп. Данная теорема дает достаточное условие для точности тензорного пополнения. Заметим, что условие 1) из определения класса рО является также необходимым. В классе Р0 содержатся свободные группы. Он замкнут относительно прямых пределов, свободных произведений и расширений специального вида. Важным следствием из этой теоремы является точность тензорного пополнения для кольца R, содержащего кольцо целых чисел Z. Для конкретных колец, например, для тел нулевой характеристики и кольца многочленов R = Z[xi,..., xn] с целыми коэффициентами, эта. теорема, доказана, в работах [11-13].

Замечание. Определим класс групп P0, более широкий, чем класс P0. Будем говорить. что группа G G P ^. если для любой ее максималыюй подгруппы M выполнено условие: M либо R-модуль, либо M удовлетворяет условиям 1) и 2) в определении класса P0. Тогда, основная теорема, справедлпва п для групп класса. P0.

Сформулируем понятие свободной MR-группы. Пусть R — ассоциативное кольцо с единицей 1, X — произвольное множество.

Определение 10. MR-группа F_R(X) с множеством R-порождающих X называется свободной MR-группой с базой X, если выполнено следующее условие: для каждой MR-группы G произвольное отображение р₀ : X ^ G продолжается до R-гомоморфпзма р : F r (X ) ^ G. Множество X называется множеством свободных MR- порождающих FR(X ). Мощность |X| называется решгом группы FR(X ).

Теорема 2. Для любых X и R свободная MR-грунна существует и единственна с точностью до К-изоморфизма.

C Пусть F(X ) — свободная группа в классе всех групп. Тогда ее тензорное MR-пополнение является свободной MR-группой с базой X. Действительно, пусть р₀ : X ^ G - произвольное отображение из X в MR-группу G:

X

F (X )

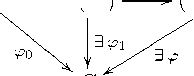
G

(F (X ))R

Тогда ро продолжается до гомоморфизма pi : F(X ) ^ G по свойству свободной группы, а последнее отображение продолжается до R-гомоморфизма р : (F(X ))^R ^ G. Следовательно. (F(X ^-свободная MR-группа с базой X.

Единственность следует из единственности тензорного пополнения. B

Сформулируем следствие из основной теоремы 1 и теоремы 2.

Следствие. Пусть R — кольцо, содержащее Z в качестве подкольца. Тогда свободная группа F(X ) точна относителыю кольца. Z. Другими словами. F(X ) является подгруппой F r ( X ).

C По теореме 2 F_R (X) = (F (X ))^R. Та к как F (X ) G P 0 и не содержит инволюций, то по теореме 1 гомоморфизм А : F (X) ^ (F (X))^R является вложением. B

Введем конструкцию свободного произведения в категории MR-rpynn.

ОПРЕДЕЛЕНИЕ 11. Пусть Gi. i G I.- MR-rpvnni ,i. MR-группа *Gi называется свобод-

R ным произведением в категории MR, если R-гомоморфизмы pi : Gi ^ *Gi таковы, что R для любых R-гомоморфизмов ^i : Gi ^ H, где H — произвольная MR-группа, существует R-гомоморфизм ф : *Gi ^ H, делающий коммутативными следующие диаграммы:

R

Gi

ψ i

ϕ i

—* Gi

R z

z

Zz 3 ^

(^i = руф, i G I )

II *Gi МН-порождается множеством {yi(gi ), gi Е Gi, i Е I }.

Из категорных соображений следует, что группа *Gi определена однозначно с точ-R ностыо до R-гомоморфизма.

Теорема 3. Пусть R — кольцо, содержащее кольцо целых чисел Z в качестве подкольца, Gi, i Е I, — некоторое множество MR-групп. Тогда

• 1)    *Gi = (*Gi.

• 2)    гомоморфизм А : *Gi ^ (*Gi ) является вложением.

C Пл-сть у0 : Gi ^ *Gi — канонические вжлкення. Так как класс Pr замкнут относительно свободных произведений [9], то к нему можно применить конструкцию тензорного пополнения. Пусть А : *Gi X- (*Gi )^R - гомоморфизм из определения тензорного пополнения. Обозначим через yi = А о у0. i е I. Тогда yi : Gi ^ (*Gi)^R есть совокупность R-гомоморфизмов. Пусть Д : Gi X- H. i Е I. - произвольные R-гомоморфизмы. Для того чтобы доказать, что группа (*Gi )^R является свободным произведением в категории M_R (т. е. доказать, что *Gi = (*Gi )^R), мы должны замкнуть диаграмму

ϕ ⁰

Gi     -*.-*.)R