О классах неинвариантных подгрупп в непериодических группах

В работах [1], [2], [3], [4] описаны конечные группы, имеющие соответственно один, два, три и четыре класса неинвариантных сопряженных подгрупп. В работе [5] описаны периодические группы, содержащие бесконечную абелеву подгруппу и имеющие конечное множество классов неинвариантных сопряженных подгрупп.

Через p ( G ) обозначается число классов сопряженных неинвариантных подгрупп группы G .

Теорема 1. Всякая непериодическая локально разрешимая группа G с конечным множеством классов неинвариантных сопряженных подгрупп абелева.

Доказательство. Пусть сначала всякая бесконечная циклическая подгруппа группы G инвариантна и пусть x и a – произвольные элементы группы G соответственно бесконечного и конечного порядка. Рассмотрим следующую цепочку подгрупп:

(x , a о ( x 2 , а о (х ² , а о ... о (2² , a о ... .

Так как x инвариантна в G, то никакие две подгруппы из этой цепочки не сопряжены в G. Отсюда и из того, что множество классов неинвариантных подгрупп группы G конечно, следует, что

инвариантна в G. Таким образом, всякая циклическая под- группа группы G инвариантна. Следовательно [6, с.213], G – абелева группа.

Предположим, что в группе G имеется бесконечная неинвариантная циклическая подгруппа x . Так как x неинвариантна в G, то найдется максимальная подгруппа подгруппы x также инвариантная в G. Таким образом, можно построить бесконечную цепочку подгрупп ll

22 jу о ( x j) о ... о ( x f j о ..., каждая из которых неинвариантна в G . Так как p ( G ) конечно, то в приведенной выше цепочке подгрупп обязательно найдутся две подгруппы, сопряженные в G . Поэтому без ограничения общности можно полагать, что найдется такое целое число k ^ 1; 0 и такой элемент x 2 , что x 2          k 1

x ।      X j •

Так как для всякого натурального числа п xX2 = xk1 и, очевидно, xk1 ^ 1, то x 2 - элемент бесконечного порядка. В силу того, что x2 – элемент бесконечного порядка и элементы x 2 и x2 неперестановочны, x  неинвари антна в G . Поэтому, как и выше, без ограничения общности можно полагать, что найдется такое целое число k2 ^ 1; 0 и такой элемент x3, что xx3 = xk2. Таким образом, для всякого натурального числа n в группе G най-

дется такая совокупность элементов

X1, x2,..., Xn+1, что xx+1 = xki, k * 1; 0   (i = 1, 2,..., n).

Покажем, что для всякого натурального числа n в группе G найдется разрешимая подгруппа ступени разрешимости n . Действительно, рассмотрим подгруппу

Sn = Xх!,X2,...-X»+1), где все элементы xi бесконечного порядка и xXi+1 = xki (к * 1; 0). Очевидно, что [xi, xi+1 ] = xki—1, и, следова тельно, X^OSSn * 1 (i = 1, 2,..n). Легко про- к -1    k:, -1      / \ верить, что [x/ ,xp+1 JeРхА и поэтому

XxtOS S„ * 1 (i = 1, 2,...,n — 1).     Продолжая этот процесс далее, получим, что Xx Os S(n) * 1. Таким образом, ступень разрешимости группы Sn не меньше, чем n.

Так как группы различной ступени разрешимости неизоморфны, то они не могут быть сопряжены в G. Отсюда вытекает, что ступень разрешимости всякой неинвариантной разрешимой подгруппы группы G не превосходит некоторого числа t. Пусть A - инва- риантная разрешимая подгруппа ступени разрешимости большей, чем p(G) +1.

^ GA ^{( 5} — ^{1 ))} " P ⁽ G ) ’ причем

Очевидно

равенство достигается только в том случае, когда подгруппа A(s-1) содержится в пересече- нии всех неинвариантных подгрупп группы G. Поэтому, в силу выбора числа s, p(G/(s-'))” p(G). Аналогично

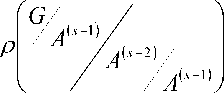
< Р

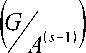
и, следо-

вательно, p ( G / ( _s — 2 ) ) < p ( G ) — 1.

Продолжая этот процесс далее, полу- чим, что p(G/ (s—p(G)))< 1. Это означает, что фактор группа G/ (s—p(G)) дедекиндова. Однако это A невозможно, так как, очевидно, факторгруппа

/ А (s—Р(G)) недедекиндова. Полученное про- тиворечие доказывает теорему.

Теорема доказана.

Теорема 2. Всякая непериодическая почти локально разрешимая группа с конечным множеством классов неинвариантных сопряженных подгрупп абелева.

Доказательство. Пусть G - непериодическая почти локально разрешимая группа с конечным множеством классов неинвариантных сопряженных подгрупп. Пусть A -инвариантная локально разрешимая подгруппа группы G , имеющая в G конечный индекс n . Ясно, что G = J Ax .

Предположим, что в A имеется бесконечное множество неинвариантных подгрупп группы G : T , T ₂,..., T_n ,..., никакие две из которых не сопряжены в A . Так как p ( G ) < да , то без ограничения общности можно полагать x — Tx, = T ( i = 1, 2,..., n ) . Поэтому подгруппы T , T ( 5 >  n + 1 ) не сопряжены в G . Действительно, для всякого элемента a e A и всякого элемента x _i из множества

^{^, x 2 ,...Х _п X axOT ⁽ ax i ) =

= x — ¹ a ¹ xxOTxx'ax i = aOTa * T S ^{( a} 1 ^e A )•

Аналогично получим, что подгруппа T _n+ 1 не сопряжена в G ни с одной из подгрупп T _s при s >  2 n + 1 и т. д. Таким образом, в группе G имеется бесконечное множество неинвариантных подгрупп { T_{kn + 1} }( к = 0,1,2,... ) , никакие две из которых не сопряжены в G . Это противоречит тому, что p ( G ) < да .

Пусть теперь в A не имеется бесконечного множества неинвариантных подгрупп группы G , никакие две из которых не сопряжены в A . Так как A - локально разрешимая группа, то, в силу теоремы 1, A - абелева группа. Отсюда вытекает, что всякая циклическая подгруппа из A инвариантна в G и, более того, всякая конечная подгруппа из G инвариантна в G . Предположим, что некоторая подгруппа Х0 неинвариантна в G . Тогда существует бесконечное множество простых чисел P таких, что для всякого p e PXy^P ^ неинвариантна в G . Предположим, что найдется такой элемент x e G и такие простые числа p ,    q из множества P , что

Xx 1 ypxj = yq4 у. Ясно, что для некоторого числа sxs е A и поэтому xs е CG (у). Поэтому, с одной стороны, ^х~sypxs^ = ^yq ^, а с другой стороны — X-~sypxs ^ = yyp ^ , что противоречиво. Следовательно, в G имеется бесконечное множество неинвариантных подгрупп yyp ,p p е P, никакие две из которых не сопряжены в G. Это противоречит тому, что p(G) < да. Следовательно, предположение о том, что y неинвариантна в G, неверно. Таким образом, всякая циклическая подгруппа из G инвариантна в G и, значит, G – абелева группа.

Теорема доказана .