О количественной модели рисков и преимуществ облачных вычислений

Сеть Flattened Butterfly с n шагами ( FBn ) [1] считается перспективной для создания плоских (однокаскадных) системных сетей на базе больших многопортовых коммутаторов-маршрутизаторов. Эта сеть получается «сплющиванием» n -каскадной k -ичной бабочки в плоскую сеть, при котором все коммутаторы с одинаковыми номерами в разных каскадах бабочки объединяются в один из расширенных коммутаторов FBn , а симплексные каналы между каскадами бабочки становятся дуплексными каналами между разными расширенными коммутаторами.

Общее число абонентов (процессоров), объединяемых FBn, составляет величину N=kⁿ , а ее диаметр (число скачков по сети между абонентами) — величину D=n. Сеть FBn состоит из M=N/k=k^{n– 1} расширенных коммутаторов, каждый их которых состоит из n коммутаторов k × k и имеет m=n ( k– 1)+1 дуплексных портов. Из них k портов используются для подсоединения k абонентов и ( n– 1)( k– 1) порт — для связи прямыми дуплексными каналами с другими коммутаторами сети. Поэтому число сетевых дуплексных каналов в FBn составляет величину R= ( n– 1)( k –1) N/k .

Принято считать, что сложность s и энергопотребление w коммутатора пропорциональны квадрату числа портов, поэтому сложность и энергопотребление расширенного коммутатора составляет величины s=b ( n ( n– 1)+1) k ² и w=c ( n ( n– 1)+1) k ². Тогда сложность S сети FBn задается как S=b ( n ( n– 1)+1) k ² N / k=b ( n ( n– 1)+1) k^{n+ 1}= b ( n ( n– 1)+1) N ^{( n+ 1)/ n}. Аналогично, для энергопотребления — W=с b ( n ( n– 1)+1) N ^{( n+ 1)/ n}.

К современным системным сетям предъявляется требование минимизации диаметра. Этому требованию удовлетворяет сеть FB2. Обратим внимание на то, что она имеет топологию полного графа (рис. 1). В ней величины S и W задаются как S=b 3 k ² N / k= 3 bk ³ и

W= 3 ck ³, т.е. величинами пропорциональными кубу числа портов отдельного коммутатора. Поэтому уменьшение числа портов коммутаторов (даже при некотором увеличении их числа) может понизить сложность и энергопотребление сети FB2 .

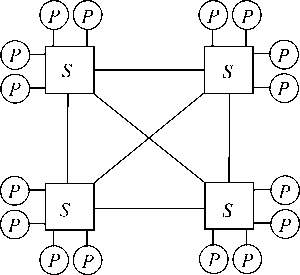
Рис. 1. Исходная сеть FB2 при k =4 ( N =16 и m =7)

В результате мы приходим к следующей постановке задачи для сети FB2 , как сети с наименьшим диаметром. Практически не изменяя число абонентов сети N, число каналов R и диаметр D , требуется уменьшить сложность S и энергопотребление W сети за счет изменения ее топологии, при котором имеет место уменьшение числа портов отдельных коммутаторов . Двойственной постановкой является требование увеличить число абонентов сети, не меняя ее сложности и коммутационных возможностей.

Возможность такой постановки задачи открывает разработка [2, 3] сетей с прямыми каналами, имеющих топологию квазиполных графов и орграфов, которые позволяют эффективно заменять в топологии сети полный граф c числом узлов N = k на квазиполный граф с числом узлов N^*=k^* ( k^*– 1)/ σ– 1 (где σ — число независимых прямых каналов между любыми двумя узлами) или квазиполный орграф с N^*= ( k^* )² (только с одним прямым каналом σ =1). В случае N=N^* это приводит к уменьшению степени узлов от k до k^* ≈ ( σm )^1/2. При схемной реализации степень узла задает число его портов.

Обоснованность такой постановки подтверждается тем, что сеть с топологией квазиполного графа или орграфа является неблокируемой при самомаршрутизации пакетов каждым источником. Это означает, что она равномощна сети с топологией полного графа на произвольных перестановках пакетов и близка к ней на случайном равномерном трафике между абонентами [4]. Последний вид трафика и имеет место между коммутаторами в FB2.

Дело в том, что сеть FBn наследует коммутационные свойства сети n -каскадная k -ичная бабочка. Поэтому сеть FBn не является ни неблокируемой, ни даже перестраиваемой, имеет только один путь между любыми двумя процессорами и, как следствие, не обеспечивает равных задержек передачи разным абонентам. Для преодоления этого недостатка приходится использовать специальные алгоритмы маршрутизации, которые и приводят к равномерной рандомизации трафика между коммутаторами. Эти алгоритмы снижают пропускную способность сети до двух раз или аналогично повышают ее эффективный диаметр (реальные задержки передачи) [1].

Статья имеет следующую структуру. Раздел 1 содержит основные понятия, используемые для описания топологии предлагаемой сплющенной сети. Эта топология задается квазиполными графами и орграфами. В разделе 1 приводится краткий обзор свойств и характеристик сетей с рассматриваемой топологией. В разделе 2 рассматривается мо- дификация сети сплющенная бабочка за счет замены полного графа на распределенный полный коммутатор и расматриваются ее свойства и характеристики. В разделе 3 рассматривается обобщенная многокаскадная сеть, получаемая из распределенного коммутатора, и строится новая сплющенная сеть, полученная сплющиванием обобщенной сети минимального диаметра. Здесь же сравниваются характеристики сплющенных сетей минимального диаметра — «сплющенной бабочки» и сплющенной обобщенной сети. В заключении подводятся итоги проведенного исследования.

1.    Квазиполные графы и орграфы Квазиполный граф QFG(M*,k*,σ*) — это однородный двудольный граф, каждую * * * долю которого составляют M узлов степени k . Значение k выбирается минимальным, при котором любые два узла в одной доле связаны σ* ≤ k* прямыми путями длины 2 через разные узлы в другой доле. Если такой граф существует, то его параметры связаны соотношением M*=k*(k*–1)/σ*+1. На рис. 2 представлена сеть с топологией квазиполного графа QFG(7, 4, 2), т.е. с двумя путями между узлами одной доли. Рис. 2. Сеть с топологией квазиполного графа QFG(7, 4, 2)

Квазиполные графы изоморфны симметричным блок-схемам, исследуемым в комбинаторике [2, 3]. Их построение сводится к построению соответствующих блок-схем, и осуществляется обычно комбинаторными методами, являющимися NP -сложными по k^*.

При схемной реализации узлы одной доли — это абоненты с k* дуплексными порта- с k* дуплексными портами. симметричная блок-схема

ми, а узлы другой доли — это полные коммутаторы k^*×k^* Таблицей инцидентности квазиполного графа является B ( M^*,k^*,σ^* ), которую задает табл. 1 для графа QFG (7, 4, 2).

Эта таблица задает схему межсоединений узлов разных долей в сети. Первая колонка задает коммутаторы, а строки — номера подсоединенных к ним абонентов.

Таблица 1

Межсоединения в QFG (7, 4, 2)

Блоки 4×4	B (7, 4, 2) QFG (7, 4, 2)
1	1	2	3	4
2	1	2	5	7
3	1	3	5	6
4	1	4	6	7
5	2	3	6	7
6	2	4	5	6
7	3	4	5	7

Нахождение прямого пути между любыми двумя абонентами сводится к нахождению номеров выходных портов абонентов и коммутаторов, однозначно задающих этот путь. Прокладка прямого канала — это просто передача короткого пакета-зонда по выбранному пути с подтверждением его приема.

Основные коммутационные свойства сети с топологией квазиполного графа состоят в следующем [2, 3]. Во-первых, это сеть с прямыми каналами. Во-вторых, эти каналы находятся и строятся путем самомаршрутизации. В-третьих, эта сеть является неблокируемой, т.е. обеспечивает бесконфликтную реализацию любой перестановки пакетов данных между абонентами, т.е. равносильна сети с топологией полного графа. В-четвертых, эта сеть является (<т-1)-отказоустойчивой по каналам, т.е. отказ (<т-1)-го канала у любых абонентов сохраняет первые три свойства. Более того, они сохраняются и при отказе любых (т-1)-го коммутаторов.

Квазиполный орграф определяется только при т=1 и для направленных дуг. Квазиполный орграф QFDG ( M^*,k^* ) — это однородный двудольный граф, каждую долю ко-

*

*

*

торого составляют M узлов степени k . Значение k выбирается минимальным, при ко-

тором любые два узла в одной доле связаны прямыми путями

длины 2 через разные уз-

лы в другой доле.

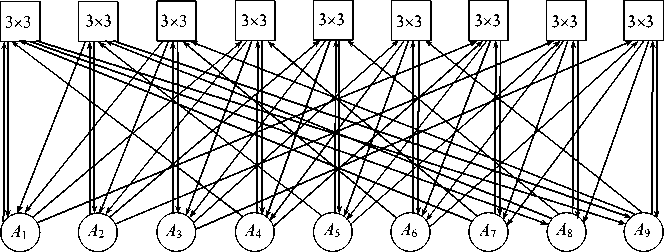
Рис. 3. Квазиполный орграф QFDG (9, 3), полученный из 2-мерного 3-ичного мультикольца [3]

Такой орграф всегда существует, и его параметры связаны соотношением M = ( к ) 2 . На рис. 3 и рис. 4 даны примеры разных квазиполных орграфов QFDG (9, 3). В этих орграфах схемы межсоединений задают табл. 2 и табл. 3 соответственно.

Таблица 2

Межсоединения в квазиполном орграфе по рис. 3

Коммутаторы 3×3	Дуги от абонентов			Дуги к абонентам
1	1	9	8	1	4	7
2	2	1	9	2	5	8
3	3	2	1	3	6	9
4	4	3	2	4	7	1
5	5	4	3	5	8	2
6	6	5	4	6	9	3
7	7	6	5	7	1	4
8	8	7	6	8	2	5
9	9	8	7	9	3	6

В общем случае при произвольном k^* на пересечении i- ой строки (1 ≤ i ≤ M^* ) и j -го столбца (1 ≤ j ≤ k^* ) в левой части таблицы содержится номер ( i – j ) mod ( M^* +1), а в правой — номер [ i +( j– 1) k^* ] mod ( M^* +1) .

При произвольном k на пересечении i- й строки (1 ≤ i ≤ M ) и j -го столбца (1 <  j <  k ) в левой части таблицы содержится номер L i / k J k + j , а в правой — номер ( i ) mod ( k^* +1)+( j– 1) k^*.

Заметим специально, что при схемной реализации квазиполного орграфа встречные пути между каждой парой абонентов на участке абонент-коммутатор задаются парой встречных симплексных каналов, которые могут быть подсоединены к разными коммутаторам и могут не образовывать дуплексных каналов. Поэтому далее в работе связи между абонентами и коммутаторами для квазиполного графа подсчитываются в числе дуплексных каналов, а для квазиполного орграфа — в ных каналов.

числе пар встречных симплекс-

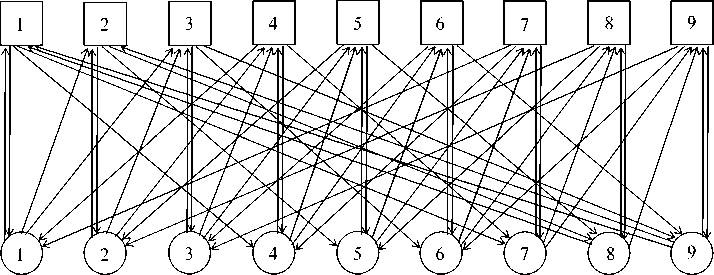
Квазиполный орграф QFDG (9, 3),

Рис. 4.

полученный из 2-мерного 3-ичного обобщенного гиперкуба

Таблица 3

Межсоединения в квазиполном орграфе по Рис. 4

Коммутаторы 3×3	Дуги от абонентов			Дуги к абонентам
1	1	2	3	1	4	7
2	1	2	3	2	5	8
3	1	2	3	3	6	9
4	4	5	6	1	4	7
5	4	5	6	2	5	8
6	4	5	6	3	6	9
7	7	8	9	1	4	7
8	7	8	9	2	5	8
9	7	8	9	3	6	9

2.    Предлагаемое решение

Сначала рассмотрим вариант изменения топологии для сети FB2, сложность и энергопотребление которой составляют величины S= 3 bN ^3/2 и W= 3 cN ^3/2. Для этого расширим FB2, заменив в ней полный граф на квазиполный граф или орграф, в котором расширенные коммутаторы FB2 являются абонентами (рис. 5). Расширенную сеть FB2 будем обозначать как ЕB2.

В EB2 к каждому расширенному коммутатору с m ^*=2 k ^*–1 дуплексными портами добавляется вторичный коммутатор с k ^*–1 портами. Каналы между расширенными и вторичными коммутаторами прокладываются согласно таблицам межсоединений в квазиполном графе или орграфе [3]. На рис. 5 используется квазиполный граф (рис. 2), который обеспечивает два прямых пути между любыми двумя первичными коммутаторами.

Любые два расширенных коммутатора в EB2 связаны через один вторичный коммутатор, поэтому формально диаметр EB2 задается как D^*= 1,5 D . Однако передачи пакетов через вторичные коммутаторы осуществляются по прямым каналам без их буферизации, и задержки в сетях FB2 и EB2 различаются только на очень малую часть длительности пакетов, т.е с практической точки зрения можно принять, что D ^* ≈ D .

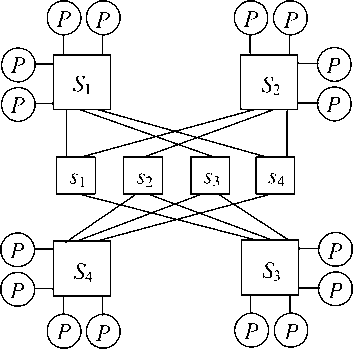
Рис. 5. Сеть EB2 при k =4 ( M^* =16 и m =7). S_i и s_i — это составные и вторичные коммутаторы соответственно. Связи между s i задает QFG (4, 3, 2)

При использовании топологии квазиполного орграфа сеть ЕB2 будет содержать M^*= ( k ^*–1)² расширенных и M^*= ( k ^*–1)² вторичных коммутаторов, и объединять N ^*= k ^* M^*=k ^*( k ^*–1)² абонентов и использовать R ^*= M^* ( k– 1) дуплексных каналов.

Сложность каждой спарки расширенного и вторичного коммутаторов составляет

—

величину   s*=3b(k*)2+b(k*–1)2≈4b(k*)2, а сложность всей сети величину

S^* = N ^* s ^*/ k ^* ≈ 4 b ( N ^*)^4/3. По постановке задачи N ≈ N ^*, поэтому имеет место оценка S / S ^* ≈ 3( N )^1/6/4. При N^* = 10³ ≈ N= 1024 имеет место оценка S / S ^* ≈ 2,4, а при N= 32 K и N^*= 33 K ( K =1024) – оценка S / S ^* ≈ 4,3. Аналогично для энергопотребления.

*

*

В сети ЕB2 с топологией квазиполного орграфа для N =1100 имеем k =11 и W ^*= c 10²(3 ⋅ 11²+10²). В сети FB2 для N= 1024 имеем k =32 и W= 3 c 32³. Поэтому при N^* ≈ N имеем W / W ^* ≈ 2,4.

Вариант сети FB2 при N ≈ 32 K в настоящее время технически нереализуем, т.к. требует составных коммутаторов с 363 портами, тогда как самой большой однокристальный коммутатор YARC [5] имеет только 64 дуплексных порта. В этом случае придется использовать сеть FBn c n > 2.

Сравним характеристики сетей ЕB2 и FB3 при N ^*=33 K и N =32 K ( K= 1024). Для ЕB2 имеем: k^*= 33, M ^*=( k ^*–1)²= K , R ^*=( k ^*–1)³=32 K и W^*=сK (3 ⋅ 33²+32²). Для FB3 имеем k= 32, M = k ²= K, R =2 M ( k –1)=62 K и W= 7 сK 32². Теперь W/W^*≈ 1,8 при R/R ^* = 1,94 и D/D = 1,5, здесь более высокое энергопотребление сопровождается еще увеличением числа каналов и задержек передачи.

В случае использования топологии квазиполного графа появляется возможность иметь несколько прямых каналов через разные вторичные коммутаторы. В частности, для EFB2 при с т = 2 можно выбрать к = 13 и получить M =1027 и W = с 12 2 (3 - 13 2 +12²), т.е. иметь W/W » 1,3 при N =1024. При с = 2 также можно реализовать вариант с k^*= 32 и M^* =16401. Правда, необходимые для этого QFG (79, 13, 2) и QFG (513, 32, 2) еще необходимо построить [6, 7].

3.    Сплющивание обобщенной сети

Обобщенными мы называем сложенные многокаскадные сети, в которых межкаскадные соединения имеют топологию квазиполного графа или орграфа [8]. В частности, 2-каскадная обобщенная сеть получается из квазиполного графа или орграфа по рис. 2 — рис. 4 заменой каждого абонента на дуплексный коммутатор k^*×k^* (коммутатор ВВ) , каждого узла другой доли — на коммутатор k^*×k^* (коммутатор хребта) , а ребра — на дуплексные каналы для графа или пары симплексных каналов для орграфа. Такая сеть объединяет N = к [ к ( к - 1 )/с +1] абонентов, если она получена из квазиполного графа, и N^* =( k^* )³ абонентов, если она получена из квазиполного орграфа.

При сплющивании 2-каскадной обобщенной сети одноименные коммутаторы ВВ и хребта объединяются в один расширенный коммутатор с m ^*=2 k^* –1 дуплексными портами. Такая сплющенная сеть состоит из M ^*= N^*/k^* расширенных коммутаторов, любые два из которых связаны 2( k^* –1) парами симплексных каналов, использует R^*= 2 M^* ( k^* –1) таких пар каналов и формально имеет диаметр D^* =3. Обозначим такую сплющенную обобщенную сеть как FG2 .

При использовании топологии квазиполного орграфа сложность сети FG2 задается выражением S^*= 4 b ( k^* )⁴ = 4 b ( N^* )^4/3. FG2 , как и сеть FB2, не является перестраиваемой и имеет только один путь между любыми двумя абонентами. Отношение сложностей FB2 и FG2 при N ® N задается выражением S / S = 3 bN ^1/6/4, т.е. таким же соотношением как и для FB2 и EB2 в предыдущем параграфе. Число сетевых портов составного коммутатора в FB2 задается величиной r = k –1= N ^1/2–1, а в FG2 — величиной r ^*=2( k^* -1)=2( N ^1/3-1).

В табл. 4 сравниваются характеристики сетей FB2 и FG2 при одинаковых размерах расширенных коммутаторов. Видно, что FG2 имеет в 6=10 раз большее число абонентов при немного меньшей удельной схемной сложности.

Таблица 4

Сравнительные характеристики сетей FB2 и FG2 для квазиполного орграфа ( K =1024)

FB2	m	k	N	M	R / N	S / N
FG2	* m	k*	N*	M*	R* / N*	S* / N*
FB2	31	16	K /4	16	0,94	48
FG2		11	1,3 K	121	1,82	44
FB2	47	24	0,56 K	24	0,96	72
FG2		16	4 K	256	1,88	64
FB2	63	32	K	32	0,97	96
FG2		22	10,4 K	484	1,81	88

Энергопотребление сетей FB2 и FG2 при одинаковом числе абонентов N =1024 ≈ N^* =1000 имеем k =32, k^* =10 и W / W ^* ≈ 2,5. При этом в сети FB2 используется R = k ( k –1)=992 дуплексных канала (1984 симплексных канала). В сети FG2 используется R^* =2( k^* )²( k^* –1)=1800 пар симплексных каналов, т.е. почти в два раза больше, чем в сетях FB2 и EB2. При этом каждый составной коммутатор в FB2 имеет r =31 сетевой порт, а в FG2 — только r^* =20 сетевых портов.

В случае использования топологии квазиполного графа в сети появляется возможность иметь несколько прямых каналов через разные коммутаторы хребта. Для этого абоненты одного расширенного коммутатора должны связываться с друг другом только через другие расширенные коммутаторы. При этом s=3bk2. В частности, для FB2 с N=1024 в FG2 c σ*=2 можно выбрать k*=13 и получить M*=79, N*=1027 и W*=c3M*132. Поэтому W/W* ≈ 2,4 и R*=2M*(k*–1)=1896 пар симплексных каналов, т.е. R*≈1,91R. Здесь опять в FB2 r=31, а в FG2 только r*=24.

В табл. 5 сравниваются характеристики сетей FB2 и FG2 при одинаковых размерах расширенных коммутаторов (в скобках приведены параметры FB2). Видно, что FG2 имеет в несколько раз большее число абонентов, в полтора раза меньшую удельную сложность и повышенную канальную отказоустойчивость и/или пропускную способ- ность.

Таблица 5

Сравнительные характеристики сетей FB2 и FG2 для топологии квазиполного графа ( K= 1024)

σ	* m	k*	N * ( N )	M*	R * / N *	S* / N* ( S / N )
2	31	11	616 ( K /4)	56	1,82	33 (48)
3			407 ( K /4)	37
2	47	16	1936 (0,56 K )	121	1,88	48 (72)
3			1296 (0,56 K )	81
2	63	22	5104 ( K )	232	1,91	66 (96)
3			3410 ( K )	155

Для топологии квазиполного графа отдельным случаем является вариант с σ^*=k ^*/2 , при котором обобщенная сеть становится 2-каскадной сложенной неблокируемой сетью [8, 9]. Она обозначается как FN2 . Для этого достаточно использовать дуплексные коммутаторы ВВ ( k^* /2) ×k^* с 1,5 k^* дуплексными портами и хребтовые коммутаторы k^*×k^* с k^* дуплексными портами. Сложность и тех и других задается как b ( k^* )². Число таких коммутаторов задается как M ^*=2 k ^*–1.

Сплющивание такой неблокируемой сети порождает неблокируемую сеть объединяющую N ^*= M ^* k ^*/2= k ^*( k ^*–1/2) абонентов, состоящую из M ^* расширенных коммутаторов с m ^*=2,5 k^* –1 дуплексными портами каждый при сложности s= 2 b ( k^* )².

В табл. 6 сравниваются характеристики сетей FB2 и FN2 при одинаковых размерах расширенных коммутаторов. Видно, что FN2 имеет в примерно в полтора раза меньшее число абонентов и немного большую удельную сложность.

Неблокируемая сеть FN2 не требует использования специальных алгоритмов маршрутизации и не испытывает сокращения пропускной способности и увеличения задержек передачи на произвольном равномерном трафике, как это имеет место у FB2 .

Таблица 6

Сравнительные характеристики сетей FB2 и FN2 для топологии квазиполного орграфа ( K =1024)

FB2	m	k	N	M	R/N	S/N
FN2	* m	k*	N*	M*	R* / N*	S* / N*
FB2	31	16	K /4	16	0,94	48
FN2		14	189	27	1,82	46
FB2	47	24	0,56 K	24	0,96	72
FN2		20	390	39	1,88	80
FB2	63	32	K	32	0,97	96
FN2		26	663	51	1,81	104

Заключение

Предложена модификация сети в расширенную сеть EB2, которая состоит в замене топологии полного графа на топологию квазиполного графа или орграфа, осуществляемая за счет введения промежуточного слоя малых коммутаторов. Она может осуществляться без изменения числа абонентов (процессоров), диаметра сети и числа используемых каналов, и обеспечивать более чем трехкратное снижение энергопотребления сети. Эта модификация позволяет многократно увеличить число абонентов при использовании коммутаторов одинакового размера без увеличения удельного энергопотребления.

Предложена новая сплющенная сеть минимального диаметра FG2 , полученная из 2-каскадной обобщенной сети, имеющая характеристики сети EB2. Сеть FG2 имеет в несколько раз большее число абонентов при равной и меньшей удельной сложности, чем сеть FB2. Сеть FG2 может иметь несколько независимых каналов между абонентами, что обеспечивает большую канальную отказоустойчивость и большую пропускную способность. Накладными расходами при этом является двукратное увеличение удельного числа проводов .

Рассмотрен предельный по числу каналов вариант сети FG2 , полученный сплющиванием нового вида неблокируемой сети — сеть FN2 . По сравнению с FB2 о на имеет примерно равное удельное энергопотребление и меньшие задержки передачи, но и меньшее число абонентов. Возможность эффективного применения сети FN2 требует дальнейшего исследования.