О конечной липшицевости классов Орлича - Соболева

Напомним некоторые определения. Борелева функция р : Rn ^ [0, то] называется допустимой для семейства кривых Г в Rn, n >  2, пи шут р Е admГ, если

j p(x) ds >  1

γ

(1.1)

для всех y Е Г. Пусть p > 1. Тогда p-модулем семейства кривых Г называется величина

Mp (Г) =

inf [ pp(x) dm(x). ρ ∈ adm Γ

Rn

(1.2)

m                  Rⁿ

Пусть D — область в Rn. n >  2. Пре дно л*>жим. что n — 1 < p < n п

M p (f Г) 6 КМр(Г)                           (1.3)

для произвольного семейства Г кривых y в области D. При предположении, что f в (1.3) является гомеоморфизмом, Герингом было установлено, что отображение f является x 0 ∈ D

If(x) — f(xo)| , lim sup ---:-------:--- 6 K n-p , x→x0      |x - x0 |

(1.4)

см., например, теорему 2 в [1].

Напомним, что гомеоморфизм f : D ^ Rn называется отобралсслисм с конечным искалсеннем. если f Е WlOC ii

kf 0(x)kⁿ 6 K (x) • J f (x)

(1.5)

для некоторой почти всюду конечной функции K (x) > 1, где f 0(x) якобиева матрица f, ||f 0(x)k - ее операторная норма: kf 0(x)| = sup|h|=₁ |f 0(x) • h| 11 J f (x) = det f 0(x) -якобиан отображения f.

Пусть p E (1, то). В дальнейшем, полагаем kf0(x)kp

K p ^(x,f ) =

J (x,f)

1,

∞,

если J (x, f) = 0;

если f0(x) = 0;

в остальных точках.

(1.6)

Впервые понятие отображения с конечным искажением введено в случае плоскости для f E W^ в работе [2]. ем. также [3].

Следуя Орличу, для заданной выпуклой возрастающей функции у : [0, то) ^ [0, то), у(0) = 0. обозшгчим символом L^ пространство всех функций f : D ^ R, таких, что

[ у (ША dm(x) < то.

(1.7)

λ

D при некотором А > 0, см.. например. [4]. Здесь m — мера. .Лебега, в Rn. Прост}жпство L^ называется пространством Орлича.

Классом Орлича - Соболева WlO^D) называется класс всех локально интегрируемых функций f, заданных в D, с первыми обобщенными производными по Соболеву, градиент Vf которых принадлежит классу Орлпна локально в области D. Если же. более того. Vf принадлежит классу Орлпна. в области D, мы пишем f E W 1^(D). Заметим, что по определению Wl¹/ С W^c¹. Как обычно, мы пишем f E Wlofp, если у(t) = t^p, p >  1. Известно, что непрерывная функция f принадлежит классу WOC тогда п только тогда, когда f E ACL^p т. е., если f локально абсолютно непрерывна на почти всех прямых, параллельных координатным осям, а первые частные производные f локально интегрируемы в степени p в области D, см. [б. раздел 1.1.3.].

Далее, если f — локально интегрируемая вектор-функция n вещественных переменных xi, . . . ,Xn, f = (fl,..., fm), fi E W^1, i = 1, . . . , m, II

J у (|Vf (x)|) dm(x) < то,                               (1.8)

D m dff-                           ^A Ф где |Vf (x)| = .M 22 \fir) , то мы снова пишем f E WiO^. Мы также используем i=1 j=1    j обозначение W^ в случае более <збших функций у, чем в классах Орлича. всегда пред полагающих выпуклость фуикцпп у п ее нормировку у(0) = 0.

Отметим, что классы Орлича. - Соболева, сейчас, как и ранее, изучаются в самых различных аспектах многими авторами, см., например, [6-22].

• 2.    Свойства классов Орлича — Соболева

Следующие свойства, классов Орлича. - Соболева, можно найти в работе [14].

Теорема 2.1. Пусть П - открытое множество в Rn. n > 3. f : П ^ Rn - непрерывное открытое отображение класса WlOy(n). в те у : (0, то) ^ (0, то) - неубывающая функция.

такая что для некоторого t* Е (0, то)

∞

Г t    n-2

J  уф).

dt < ∞.

(2.1)

t ∗

Тогда отображение f имеет почти всюду полный дифференциал в П.

Замечание 2.1. В частности, заключение теоремы 2.1 имеет место, если f Е W^" при некотором a > n - 1. Последнее утверждение - результат Вяйсяля, см. [23, лемму 3]. Теорема 2.1 является также распространением в пространство R хорошо известной теоремы Меньшова — Геринга — Лехто на плоскости, см., например, [24-26].

Теорема 2.2. Пусть П - открытое множество вГ,п > 3, f : П Ж Rn - непрерывное открытое отображение класса W^H), ул у : (0, то) Ж (0, то) - неубывающая функция. удовлетворяющая условию (2.1). Тогда от(эбражеппе f имеет почти всюду поливен дифференциал в П

Теорема 2.3. Пуств U - открвыое множество в Rn, n >  3, у : (0, то) — (0, то) - неубывающая функция, удовлетворяющая условию (2.1). Тогда любое непрерывное отображение f : U — Rm. m > 1. кжюса W^ обдалает (N Усвойством. более того, локально абсолютно непрерывно относительно (n - 1)-мерной хаусдорфовой меры на почти всех гиперплоскостях P, параллельных произвольной фиксированной гиперплоскости P0. Кроме того, па почти всех таких P. H ^n-1(f (e)) = 0. ее ли |Vf | = 0 на E С P.

Заметим, что, если условие вида (2.1) имеет место для некоторой неубывающей функ-щш у. то функция Vc(t) = y(ct) щже > 0 также удовлетворяет соотношению (2.1). Кроме того, хаусдорфовы меры являются квазиинвариантными при квазиизометриях.

Следствие 2.1. При условии (2.1) любое непрерывное отображение f Е W^ обладает (N ^-свойством относительно (n - 1)-мерной меры Хаусдорфа, более того, локально абсолютно непрерывно на почти всех сферах S с центром в заданной предписанной точке х₀ Е Rn Кроме того, на почтп всех таких сферах S выполнено условие H^n-1(f (E)) = 0 как толвко |V f | = 0 па миожостве E С S.

• 3.    Модули семейств поверхностей

Следуя [27, раздел 9.2], далее k-мерной поверхностью S в Rn называется произвольное непрерывное отображение S : ш - Rn. г.те ш - открытое множество в Rk := R^k и{то} и k = 1,... ,n — 1. Функцией кратности поверхности S называется число прообразов

N(S, y) = card S ¹ (y) = card {x Е ш : S(x) = y}, y Е Rn.

Другими словами, символ N(S,y) обозначает кратноеть накрытия точки y поверхностью S. Известно, что функция кратности является полунепрерывной снизу, и, значит, измерима относительно произвольной хаусдорфовой меры H^k, см. [27, раздел 9.2].

Для борелевскон «Ьункщш р : Rn - [0, то] ее интеграл наD побсрдностъю S опреде ляется равенством

ρ dA

S

:= У p(y) N (S,y) dH^ky.

Rn

Пусть Г — семейетво k-мерыых поверхностей S. Боре.тева функция р : Rn ^ [0, то] называется допустимой для семейства Г, пи шут р Е admГ, если j рк dA > 1

(3.1)

S для каждой поверхности S Е Г. Пусть р Е (1, то) — заданное фиксированное число. Тогда р-модулсм <•емейства Г называется величина.

М_Р(Г) = inf [ pp(x) dm(x). ρ ∈ adm Γ

(3.2)

Rn

Говорят, что свойство P имеет место для р-почти всех (р-п.в.) k-мериых поверхностей S семейетва Г, если подсемейство всех поверхностей семейства. Г. для которых

Pp

• 4.    О емкости конденсатора

Следуя работе [28], пару = = (A, C), г де A С Rn — открытое множество и C — непустое компактное множество, содержащееся в A, называем конденсатором. Конденсатор = называется колы.,свилi конденсатором, если G = A \ C - ко.твпо. т. е.. если G — область, дополнение которой Rn \ G состоит в точности из двух компонент. Говорят также. Tito конденсатор = = (A,C) лежит в области D. если A С D. Очевидно. что если f : D ^ Rn - непрерывное. OTiq>ытое отображение н = = (A, C ) - концеисатор в D. то (fA, fC) также кон.тенсатор в fD. Далее f = = (fA,fC).

Функция u : A ^ R абсолютно непрерывна на прямой, имеющей непустое пересечение с A, если она абсолютно непрерывна на любом отрезке этой прямой, заключенном в A. Функция u : A ^ R прииадлежнт классу ACL (абсолютно непрерывна на почта всех прямых'), если она. абсолютно непрерывна, на. почти всех прямых, параллельных любой координатной оси.

Обозначим через C0(A) множество непрерывных функций u : A ^ R1 е компактным носителем. W0(=) = W0(A,C) - семейство пеотрицате.тьиых функций u : A ^ R1 таких, тио 1) и Е C0(A). 2) u(x) > 1 д.тя x Е Си 3) и припадлежнт классу ACL. Также обозначим n            2  1/2

X .

∂x i=1

Пуств G - область в Rn. n > 2. E,F С Rn - пропзво.твпыо множества. Обозиатшм тюрез A(E,F; G) семейство всех кривых y : [a,b] ^ Rn, которые соедпиятот E ii F в G, т. о. Y(a) Е E. Y(b) Е F н y (t) Е G при a < t <  b.

р >1

capp = = capp (A, C )

= inf u∈W0(E)

/|^{w|p dm ( x )}

A

(4.2)

называют р-емкостъю конденсатора =. Емкости в контексте теории отображений хорошо представлены в монографии [29].

В дальнейшем при р > 1 мы будем использовать равенство capp = = Mp(A(dA, dC; A \ C)),

(4.3)

cm. [30-32].

Известно, что при 1 6 p < n p n - p            n-p

(4.4)

(4.6)

capp E > nvn I ----- [m(C)] n , где vn — объем единичного шара в Rn, см., например, неравенство (8.9) в [33]. Если множество C связно, то при n — 1 < p 6 n имеет место оценка n-1        d(C)p

(capP E)   > Ym(A)i-+p где d(C) — диаметр множества C, 7 — положительная константа, зависящая только от размерности n 11 p, см. предложение 6 в [34].

• 5.    Нижние Q-гомсоморфизмы относительно p-модуля

Говорят, см. [27, раздел 9.2], что измеримая по Лебегу функция р : Rn ^ [0, то] является обобщенно p-dornjcrnuMou для семейства. Г. состоящего из (n — 1)-мсриых поверхностей S в Rn. пи шут р Е extp admH если

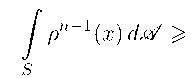
У p^n-1(x) dA >  1

S

(5.1)

для p-почти всех S Е Г.

В работе [35, раздел 13], Ф. Геринг определил K-квазиконформное отображение как гомеоморфизм, изменяющий модуль кольцевой области не более чем в K раз. Следующее понятие мотивировано кольцевым определением Геринга.

Пусть D II D0 - области в Rn. n >  2. x₀ Е D. Q : D ^ (0, то) измеримая по Лебегу (функция. Гомеоморфизм f : D ^ D0 будем называть hudichum Q-гомеоморфизмом относительно p-модуля в точке хо, если

M_p (f Е_е) >    inf f ^x dm(x)

pOextp admS_E J Q(x) R

(5.2)

для каждого кольца.

R = R(x₀, e,e₀ ) = {x Е Rn : E <  |x — x₀| < £0} , E Е (0, E₀ ), E₀ Е (0, d₀), где do = dist(xo,dD), a E_e обозначает семейство всех сфер

S(x₀,r) = {х Е Rn : |х — х₀1 = r} , r Е ( e,e₀ ).

(5.3)

Qp менима, в частности, к отображениям квазиконформным в среднем, см. [34, 36], и к так называемым (p, q)-квaзикoнфopмным отображениям, см. [37], которые использовались при изучении проблемы Ю. Г. Решетника о суперпозиции функций пространств Соболева, см. например, [37-40]. В работах [41-43] приводятся приложения нижних Q-гомеоморфизмов к исследованию локального и граничного поведения гомеоморфных решений с обобщенными производными и к задаче Дирихле для уравнений Бельтрами с вырождением.

Исторически нижним Q-гомеоморфизмам относительно p-модуля предшествовали Q-гомеоморфизмы, которые исследовались в работах [44-47]. Кроме того, Q-отображения допускающие точки ветвления, изучались в работах [48-53].

Ниже приведен критерий нижних Q-гомеоморфизмов относительно p-модуля при p >  n — 1. Впервые критерий был доказан при p = n в работе [54. теорема. 2.1]. см. также монографию [27, теорема. 9.2].

Лемма 5.1. Пусть D - область в!¹¹, n >  2. x ₀ G D. ii пусть Q : D ^ (0, to) - измеримая функция. Гомеоморфизм f : D ^ Rn является ппжппм Q-гомеоморфизмом в точке x₀ относительно p-модуля при p > n — 1 тогда и только тогда, когда

Mp(fЕ6) > [     dr kQk n-1 (r)

£       P— П +1

^(V E ^{G (0,} Eo ), ^E0 ^{G (0,} do ^)),

(5.4)

где d₀ = dist(x₀, dD), E_e — семейств о всех сфер S(x₀, r) = {x G Rⁿ

r G ( e,E 0). и

kQk _n-L (r) = p-n +1

(/

x S(xo,r)

n- 1

Q p^-n+1 (x) dA

p-n +1 n 1

| x — X0I = r}.

(5-5)

Инфимум в (5.2) достигается только для функции

P0(x) =

Q(x)       ! ^p-n

(5.6)

kQk (|x — X0I) p-n +1

Q p-модуля, приведем вспомогательную лемму 9.2 из монографии [27].

Лемма 5.2. Пусть (X, д) - измеримое простраиство с конечной мерой ц. q G (1, то), и пусть р : X ^ (0, то) — измеримая функция. Положим

I (p,q) = inf α

/

X

ϕ αq dµ,

(5.7)

где инфимум берется по всем измеримым функциям a : X ^ [0, то] таким, что

j a dp = 1.                                   (5.8) X Тогда I(p,q)= J- d dp ,                           (5-9) X где А = q0, 1 + A = 1,                            (5Л°) q q q0 те. А = 1/(q — 1) G (0, то). Кроме того, инфимум в (5.7) достигается только для функции a0 = C • р А,

(5.П)

где

C =

ϕ-λ dµ

X

(5.12)

C Доказательство леммы 5.1. Заметим, что для каждой Р € extp admX£ «функ ция

Ap(r):= J

S(x 0 ,r)

pn ¹ (x) dA = 0

и. в.

является измеримой по параметру r, например, по теореме Фубини. Таким образом, мы можем требовать выполнения равенства. A_p(r) ж 1 п.в. вместо условия допустимости (3.1) при k = n — 1. ii

■ f       f pp(x)n ( I 7 v f aq (x) , !

inf      6НГТ dm(x) = inf —— dA dr, pEextp admZy J Q(x)                aeI(r) J Q(x)

Rε                       ε             S (x 0 ,r)

где q = p/(n — 1) > 1. а нсрез I (r) обозначено множество в сек измеримых функций a(x)

на поверхности S(xo, r) таких, что

j  a(x) dA = 1.

S(x 0 ,r)

Итак, лемма 5.1 следует из леммы 5.2 при X = S(xo, r), у   (n — 1)-мерная площадь на S(xo,r), у = Q1|S(x0,r), и q = p/(n — 1) > 1. B

Таким образом, неравенство (5.4) является точным для нижних Q-гомеоморфизмов относительно р-модмтя.

Лемма 5.3. Пусть D - область вПР n > 2. x₀ € D. ii пусть Q : D ^ (0, w) - измеримая функция ii f : D ^ Rⁿ -ш шшй Q-гомеоморфизмом в точке x₀ относительно p-модуля при р > n — 1. Тогда имеет место оценка

_- n- 1

r 2                        p-n +1

f dr \ dr

(5.13)

J II QI n- i (r)

r₁        p-n +1

где Sj = S (xo, rj ). j = 1, 2.

C Действите.тыю. пусть 0 < r1 < r₂ < d(x₀,dD) 11 Si = S(x₀,ri), i = 1, 2. Согласно неравенствам Хессе и Цимера (см., например, [31] и [55]),

M _Р+_ (f (A(S1, S2, D))) 6---n-i¹-------,                 (5.14)

pn                  M_P^P^+ (f (^))

поскольку f (X) С X (f (Si), f (S2), f (D)), гдe X обозначает совокупность всех сфер с центром в точке x₀, расположенных между с<]>ерамп S1 11 S2, а X (f (S1), f (S2),f (D)) состоит из всех (n — 1)-мерных новерхностен в f(D), отделяющих f(S1) 11 f(S2). Из соотношения (5.14) по лемме 5.1 вытекает заключение леммы 5.3. B

• 6.    Взаимосвязь нижних Q-гомеоморфизмов с классами Орлича — Соболева

Напомним, что отображение g : X ^ Y между метрическими пространствами X II Y называется литшшцсвым. если dist (g(x1 ),g(x₂)) 6 M • dist (х1,х₂) для некоторой постоянной M <  тон в сек x1. х₂ Е X. Говорят, что отображение g : X ^ Y билипшицсво. если, оно, во-первых, липшицево, во-вторых, M * • dist (х1 ,х₂) 6 dist (g(x1),g(x₂ )) для некоторой постоянной M * > 0 ii в сек x1. х₂ Е X.

Следующее утверждение является ключевым для дальнейшего исследования.

Лемма 6.1. Пусть D п D0 - области в Rn n > 3. у : (0, то) ^ (0, то) - неубывающая функция, удовлетворяющая условию (2.1). Тогда любой гомеоморфизм f : D ^ D0 конечного искажения класса W^ является ппжшш K_p(x,f Угомеоморфишом относительно p-модуля с p > n - 1.

C Обозпач!IM через В (борелево) множество веек точек х Е D, где отображение f имеет полный дифференциал и J_f (х) = det f0(x) = 0. Заметим, что множество В представляет собой не более чем счетное объединение борелевских множеств Bl, l = 1, 2,..., таких что отображения fl = f |Bl являются билипшицевыми гомеоморфизмами, см., например, в [56, лемма. 3.2.2]. Без ограничения общности, можно считать, что множества. В_/ попарно не пересекаются. Обозначим также через В* оставшееся множество веек точек х Е D, где f имеет полный дифференциал. однако, f0(х) = 0.

По теореме 2.1 множество В0 := D \ (В S В*) имеет меру Лебега, нуль. Следовательно, по теореме 9.1 в [27] имеем, что H ^n-1(B0 П Sr) = 0 для p-почти веек сфер Sr := S(x₀,r) с центром в произвольной точке х₀ Е D, где «p-почти все» определяется в смысле p-модуля семейства поверхностей. Тогда, в силу леммы 9.1 в [27], H ^n-1(B0 П Sr ) = 0 для почти веек r Е R и по следствию 2.1 получаем, что H^n-1(f (В_о) ПSr*) = 0 11 H^n-1(f (В*) ПSr*) = 0 для почти веек r Е R. г.те Sr* = f (Sr).

Заметим, что !«■ H"^-1(f(Bo) ^П s;) = 0 ,, H"^-1(f(B.) ^П S*) = О ДЛЯ ПОЧТИ Ж-Д сфер Sr := S (xo,r) в смысле p-модуля семейства поверхностей. Действительно, пусть Г_о - подсемейство веек сфер Sr := S(x₀,r), для которых либо H ^n-1(f (В_о) П Sr*) > 0, либо H^n-1(f (В*) П S*) > 0. Обозначим через R множество всех r Е R, для которых либо H"^-1(f(So) ^П S;) > °, .* H"^-1(f(B.) ^П S;) > 0. В силу ташиги Г.ЫШЯ MR) = °. Тогда по теореме Фубини m(E ) = 0, где Е = {х Е D : |х — хо | = r Е R}. Функция р1 : Rn ^ [0, то], определенна я символом то щ>и х Е Ен равная нулю на. оставшемся множестве обобщенно p-допустима, д.тя семейства. Г_о. Таким образом, по (9.18) в [27] М_р(Г₀) 6 RE рpdm(x) = 0, т. о.. действительно. М_р(Г₀) = 0.

По теореме Кирсбрауна, см. [56, теорема 2Т0.43], каждое отображение fl может быть продолжено до липшицевского отображения fl : Rn ^ Rn, которое по теореме Радемахера — Степанова f/ дифференцируем о почти всюду в Rn, см. [56, теорема 3.1.6]. В силу единственности аппроксимативного дифференциала, см. в [56, и. 3.1.2], можно считать, что при всех х Е Bl выполнено равенство //(х) = f0(х).

Пусть Г обозначает семейство всех с.(]>ер Sr. r Е (е,е₀ ). е₀< d₀ = dist(x₀,dD). Для произволвиой <1>упкп1ш р* Е adm f (Г), такой что р* ж 0 bi io f (D). пола гаем р ж 0 bi io D ii на. B_o, ii

р(х) := р*(f (х))kf 0(x)k при х Е D \ Во = В U В*.

Рассуждая покусочно на каждом В/, l = 1,2,..., согласно [56, раздел 1.7.6], а также используя геометрический смысл величины kf 0(х)к и ее связь с якобианом отображения.

см., например, соотношения (2.5) и (2.6) в [57, гл. I, §2], имеем, что j Pn-1 dA = j PTHf (x))kf 0(х)1Г1 dA

Sr              Sr

= j p4^-1(f (x)) •

Sr

fx)F± dA∗ dA

dA dA >  J,r4^f to)

Sr

d A ∗ d A

<Л

= j P* 1(y)dA* > 1

Sr∗ для почти всех Sr, и, следовательно, р Е extp admr. Используя замену переменных на каждом Bl, l = 1, 2,..., см., например, [56, теорема 3.2.5], ввиду счетной аддитивности интеграла, получаем также оценку

J Kppxf) dmx ⁶ /

D                        f(D)

Pp(x) dm(x),

что и завершает доказательство. B

Следствие 6.1. Любой гомеоморфизм с конечным искажением в Rn, n > 3, класса W lOC щ ш a>n — 1 является ппжшш K_p(x, f Угомеомор фииюм с p> n — 1.

Заметим, что соответствующий плоский случай был изучен в работах [58], [41-44], где установлено, что любой гомеоморфизм f конечного искажения на плоскости является нижним Q-гомооморфизмом.

• 6.1.    Конечная липшицевость классов Орлича — Соболева. Для непрерывного отображения f : D ^ Rn 1i x Е D C Rn. положим

  L(x, f) = limsup

  y→x

  
  

  If(У) - f(x)l |y-x|

  
  

  (6.1)

  
  

Говорят, что отображение f является конечно линшицевым, если L(x, f ) < то для всех x Е D.

Пусть Q : G ^ [0, то] — измеримая функция. Для любого измеримого множества

E ⊂ Rⁿ

- Qto

E

1 m(E)

j^Q(x) dmto.

E

Теорема 6.1. Пусть D и D' — области в Rn, n > 3. Предположим, что f : D ^ D' — гомеоморфизм с конечным искажением класса W^, ущ р : (0, то) ^ (0, то) - неубывающая функция, удовлетворяющая условию (2.1) и, кроме того, при p Е (n, n + ^--2)

p-n+1

Тогда.

n-1

k_p(xo )= limsup —     [K_p(x,f)] p-n+1 dm(x)

ε→0      B (x0,ε)

n-1

< ∞.

|f(x) — f(x0)| ,        ,p-n

L(xo, f) = limsup----j--------j---- 6 cn,p • kpp (xo) < то, x→x₀      |x - x0 |

(6-2)

(6.3)

cn,p                                                                                           n и р.

C Рассмотрим с<1»ерпческое кольцо R = R(x0,E1,E₂) с 0 < E1< E2 такое, что R(xo,Ei,Е2) С D. Тс)гца E = ^В (xo,E2) ,B (xo,Ei)) - кольцевой конденсатор в D и f E = f В (x₀,E₂) ,fB (x₀,Ei)) - кольцевой конденсатор в D'.

Пмлв Г* = A(fSbfS2,fR). г ле Sj = S (x0)r.,-). j = 1, 2. Тогда согласно (4.3). имеем равенство cap p f E = M(Г*).                            (6.4)

p—n+1           p—n+1

По лемме 5.3 получаем, что n 1

/ 52                         \ - p —n+1

dr cap p—+ fE 6 I/ k Kp (x,f)k     (r) I .               I6-'

ул              p—n+1   /

p —n+1 )n 1

где || Kp(x,f )k n—1(r) = p—n+1

Заметим, что

/n—1

k Kp(x,f )k p—1(r)

p —n+1

dr n 1

k Kp(x,f )k T1 (r)

p —n+1

(6.6)

Применяя теорему Фубини и неравенство Гёльдера с q = у—p+y- q' = n—i, имеем

dr k Kp(x,f)k -м—1_(r) p—n+1

n 1 p —n+1

1                           n—1

6 --------—— [Kp(x,f)]^p—n+1 dm(x).

(E2 - Ei) p—n+1

R

(6.7)

Комбинируя неравенства (6.7) и (6.5), получим

cap p p —n+1

1                           n—1

f E 6 --------—^~ [Kp(x,f)]^p—n+1 dm(x).

(E2 - Ei) p—n+1

R

(6.8)

Далее, выбирая E1 = 2e ii e₂ = 4e. получим

cap p (fB(xo, 4E),fB(xo, 2e)) 6 p-n+1

(2e)p^—n+1

j [Kp(x,f)]

B(xg,4e)

n 1 p —n+1

dm(x) .

(6.9)

С другой стороны, в силу неравенства (4.4) вытекает оценка

____________ n (p — n +1) — p cap p   (fB(xo, 4E),fB(xo, 2e)) > ci [m(fB(xo, 2e))] n(p—n+1) ,         (6.10)

p-n+1

c1                                                                                             n ii p.

Комбинируя (6.9) и (6.10), получаем, что m(fB(xo, 2e)) m(B(xo, 2e))

-

J B(x₀,4e)

n 1

[K_p(x, f)]^p—n+1dm(x)

n(p-n+1) n(p —n+1) —p

(6.11)

c2                                                       n p

Далее, выбирая в (6.8) E1 = е п E2 = 2е. получил cap p (fB(xo, 2e)JB(xo,e)) 6

p-n+1

1                            n— 1

p           [Kp(x,f)]^p—n+1 dm(x).

ε p-n+1

B (x0,2ε)

(6.12)

С другой стороны, в силу неравенства (4.5), получаем о ----n^f    dp    (fB(xo,e))

cap p    (fB(xo, 2E),fB(xo,e)) > c3          p---------------- p—n+1                                  m1-n+    ■ (fB(xo, 2e))

где сз па™.™ кочетапта. зависящая только от n и p.

Комбинируя (6.12) и (6.13), получаем, что

Г

-1

,

(6.13)

i2

d(fB(xo,E))       /m(fB(xo, 2e)) \     Г                  n1

,

(6.14)

-----;-----6 c4 —тд?——     [KP(x,f)] p—n+1 dm(x)

e                m(B(xo, 2e)) / \7b(x₀,2e)

где

.    (1 — n)(p — n + 1) + p .    (n — 1)(p — n + 1)

1                 p             ,2              p и C4  in™.™ кош тапта. зависящая толвко от n п p.

Эта. оценка, вместе с (6.11) дает неравенство j1

d(fB(xo,E))                             n—i

------------- 6 С5 —      [Kp(x,f)]^p—n+1 dm(x)

ε                    B(x0,4ε)

j2

n-1

,

(6.15)

x —      [K_p(x,f)]^p—n+1 dm(x)

B (x0,2ε)

где n ((1 — n)(p — n + 1) + p) (p — n + 1)    .    (n — 1)(p — n + 1)

1            p (n(p — n + 1) — p)         ’ ^2

n C5   положительная кош тапта. зависящая толвко от n п p.

Переходя к верхнему пределу при e ^ 0, получаем

If (x) — f (хо)|             d(fB (хо,е))r_

L(x0, f) = limsup---:-------:--- 6 limsup------------- 6 c • [kp(x0)]p—n, xmxo     |x — xo|         e^0

c n pB

Следствие 6.2. Пусть D n D - областп rP6 n > 3. Прслпол<зжть что f : D ^ D - гомеоморфизм с коне'шым искажением класса W^ с усл.ibiicm (2.1) и. кроме того, при p G [n,n + n-2)

lim sup ε→0

—"     [Kp(x,f)]

B(x0,ε)

n-1

^p—n+1 dm(x)< to

(Vxo G D).

(6.16)

Тогда гомеоморфизм f является конечно липшицевым.

Замечание 6.5. В соответствии с леммой 10.6 в [27] конечно липшицевые отображения обладают N-свойством относительно хаусдорфовых мер и, таким образом, являются абсолютно непрерывными на. кривых и поверхностях.

Построим пример гомеоморфизма с конечным искажением, не являющегося конечно липшицевым.

ПРИМЕР. Предположим, что p G (n,n + n-2)- Пусть f : Bn ^ Bn. n

> 3. где

^{1 + (}P -ⁿ⁾ [

|x|

dt

p —n+1

t^{p —n+1} ln n—1 ( e )

p-n

при x=⁰« f⁽⁰⁾ = ⁰

Касательная и радиальная дилатации f на сфере |x| = r, r G (0,1), тотся:

легко вычисля-

и

.        If (x)l

"T = I I

|x|

1 + (p - n) R-----dp——— r tp — n+1 ln n—1 (e)

p-n

r

δr

1 + (p - n) / r

dt p —n+1 tp—n+1 In "М—Г" ( e)

p —n+1 rp—n⁺¹ ln n—1 ( e )

p —n+1p-n

.

δT > δr p—n+1        p—n+l e

.

"T     = Or ln ^n—1   -

Следовательно, ввиду сферической симметрии мы видим, что

δp

Kp (x,f) =---T— pv ’     On 1 dr

§T~n+1

δr

p — n+1 = ln n—1

e

|x| .

Очевидно, что

n—1

limsup —    [Kp(x,f)] p-n⁺¹ dm(x) = тс .

с >0    B(0,e)

If (x)l

Тем не менее, как легко проверить по правилу Лопиталя, 1 |Х| ^ тс f при x ^ 0. т. е.