О коррекции эффекта перекрытия дифракционных порядков в спектрометре на основе схемы Оффнера

Широкий круг задач оперативного мониторинга земной поверхности может быть эффективно решён с использованием малых космических аппаратов (КА), несущих компактную гиперспектральную аппаратуру (ГСА). Перспективными спектрометрами для использования на малых КА являются изображающие спектрометры в конфигурации Оффнера [1-7]. Основными преимуществами таких спектрометров являются их компактный размер и возможность снижения хроматических аберраций и дисторсии до низкого уровня. В простейшем случае спектрометр Оффнера содержит два концентрических зеркала. В качестве диспергирующего элемента используется дифракционная решётка, выполненная на одном из зеркал [1-5, 7], или призма, расположенная между зеркалами [5-7]. Использование дифракционной решётки позволяет достичь большей компактности и меньших хроматических аберраций. В то же время при широком спектральном диапазоне использование дифракционной решётки приводит к негативному эффекту перекрытия спектров, формируемых в различных дифракционных порядках. Действительно, из формулы дифракционной решётки несложно показать, что для излучения кратных длин волн X , X /2, X /3,..., X / m направления распространения порядков дифракции с номерами +1,...,+ m (или -1,...,- m ) будут совпадать. В качестве примера рассмотрим компактный спектрометр Оффнера с дифракционной решёткой из работы [1], ориентированный на анализ минералогического состава и предназначенный для использования на спутниках, летающих на низких орбитах. Данный спектрометр рассчитан на диапазон длин волн от 400 нм до 3000 нм при спектральном разрешении в 10 нм. В данном случае направления отражённых дифракционных порядков с номерами +1,...,+7 будут совпадать, например, для длин волн X m = m ^2800 нм, m =1,...,7. Для устранения эффекта перекрытия порядков в спектрометр дополнительно вводятся спектральные фильтры, отсекающие нерабочие дифракционные порядки. Создание таких фильтров, а также их интеграция в спектрометр является сложной задачей.

В настоящей работе проведён анализ работы спектрометра Оффнера в параксиальном приближении и показано, что эффект наложения спектров может быть скорректирован за счёт простой обработки зарегистрированного изображения.

Спектрометр на основе схемы Оффнера

Стандартный спектрометр на основе схемы Офф-нера состоит из двух концентрических зеркал 1 и 2 с радиусами 2 R и R соответственно [1,2,7]. Зеркало 2 содержит дифракционную решётку (рис. 1).

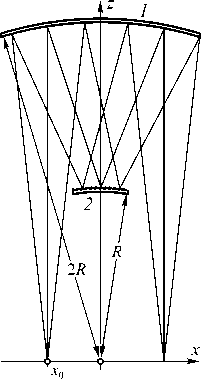
Рис. 1. Оптическая схема Оффнера

Данный спектрометр используется вместе с объективом, формирующим изображение наблюдаемого объекта в плоскости z =0. С помощью щели из формируемого изображения выделяется строка. Пусть щель расположена вдоль оси Oy при x = x ₀. Система из двух указанных зеркал в параксиальном приближении переносит изображение щели из точки x = x ₀ в точку x = - x ₀ (рис. 1). Диспергирующим элементом является дифракционная решётка на зеркале 2, которая формирует спектр щели в окрестности точки x = - x 0 .

Проведём анализ работы спектрометра. Для простоты рассмотрим двумерный вариант схемы (рис. 1). Анализ выполним в параксиальном приближении. Сначала предположим, что дифракционной решётки на зеркале 2 нет.

От источника (щели) на зеркало 1 падает цилиндрическая волна со следующей функцией эйконала:

Y ( X , Z ) = \ z 2 + ( x - x 0 ) 2 ” z + ⁽ x ,x 0 ) .           (1)

2 z

Рассмотрим отражение от зеркала в рамках приближения тонкого оптического элемента. В этом приближении набег (изменение) эйконала с точностью до константы описывается выражением:

Обозначим Ψ _gr ( x ) набег эйконала, соответствующий решётке. В этом случае формула (6), описывающая эйконал после отражения от зеркала 2, примет вид:

Y 2 ( x ) = ( x ^ + Y gr ( x ) + C 2 .

AY , ( x ) = 2 z 1 ( x ) = 2V ( 2 R ) 2 - x² = - 2 R + 4 R ,

где z = z 1 ( x ) – уравнение 1-го зеркала. Соответственно, эйконал волны после отражения от зеркала примет вид:

Y 1 ( x ) = Y ( x ,2 R ) + AY 1 ( x ) =

= 2R + (x - x0)2 - x- + 4r =(3)

4R2

^{( x + x} o ⁾² ,

=+ C ,

4R где С1 – константа, несущественная для последующего анализа. Заметим, что эйконал (3) в параксиальном приближении соответствует эйконалу сходящейся цилиндрической волны с фокусом в точке (–x0, 0). Таким образом, отражённый от зеркала 1 пучок с точностью до константы имеет следующий эйконал:

Y 1 ( x , z ) = - ( x^x ⁰)².                             (4)

2 z

Данная волна далее падает на зеркало 2. В приближении тонкого оптического элемента набег эйконала при отражении от зеркала 2 с точностью до константы описывается выражением:

AY₂ ( x ) = - 2 z ₂ ( x ) = - 2V R ² - x ² = x — 2 R .     (5)

R

Таким образом, эйконал волны после отражения от зеркала 2 примет вид:

Y₂ ( x ) = - ⁽ x ⁺ x ^o) 2 + — - 2 R = ⁽ x x ^o) 2 + C .   (6)

²         2 R     R          2 R      ²

Сформированный эйконал в параксиальном приближении соответствует эйконалу расходящейся цилиндрической волны с фокусом в точке ( x ₀,0). Таким образом, при последующем отражении от первого зеркала мы получим сходящийся цилиндрический пучок с центром в точке (– x 0 , 0).

Итак, было показано, что система двух концентрических зеркал с радиусами R и 2 R в параксиальном приближении переносит точку ( x 0 , 0) в точку (– x ₀, 0), то есть имеет коэффициент увеличения M = –1. Несложно показать, что в параксиальном приближении указанный результат остаётся верным для произвольной точки щели с отличной от нуля координатой у. При этом изображением точки щели ( x ₀, y ₀, 0) будет точка (– x ₀, –y ₀, 0). Вышеприведённый результат можно также получить, используя параксиальную формулу отражения в сферическом зеркале.

Рассмотрим далее случай, когда на зеркале 2 расположена дифракционная решётка c периодом d .

Пусть сначала щель является монохроматическим источником излучения с длиной волны λ. Тогда фазовая функция отражённой волны (7) с точностью до константы будет описываться выражением:

Ф 2 ( x ) = k O^ x - x T- ⁺ k 0 ^Y gr ( x ) ,                 ⁽⁸⁾

2 R

где k 0 =2π/λ – волновое число. С учётом периодичности функции Ψ gr ( x ) (период d ), комплексную амплитуду отражённого поля w ₂( x )=exp{i ф 2 ( x )} представим в виде [8]:

w ₂ ( x ) = exp < i k 0

^{( x - x} o ⁾²

2 R

• E ^c n exp n

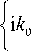
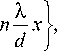
где c_n – коэффициенты Фурье, которые задаются следующим выражением:

c n ( X ) = 4fexp | i k 0 Y gr ( x ) - i² ^ nx | d x = d о I                  d J

= J exp { i k ₀ Y gr ( xd ) - i2 n nx } d x .

Отражённое поле (9) соответствует суперпозиции световых пучков (дифракционных порядков) с фазовыми функциями:

Ф ( x ) = k„ ——x ⁰)- + k„n — x = n 0 2 R      0 d

k ₀

2 R

x ₀

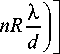
+ C n .

В параксиальном приближении фазовые функции (11) описывают расходящиеся цилиндрические пучки с фокусами в точках xn = x0-nRX/d, n=0,±1,±2, Таким образом, при последующем отражении от первого зеркала в плоскости z =0 будет формироваться набор точек (дифракционных максимумов) с координатами xn (X) = -x0 + nRX, n = 0,±1,±2,....              (12)

n 0 d

Значения энергии I n (λ) в точках x n (λ) будут описываться квадратами модулей коэффициентов Фурье (10) [8]:

I n ( X ) = C n ( X )|², n = 0, ± 1, ± 2,...                (13)

В случае, когда щель является полихроматическим источником излучения с длинами волн Xe [ X min , X max ], в каждом дифракционном порядке будет формироваться спектр с шириной

A x„ = nR —, n = 0, ± 1, ± 2,..., n d

где AX = X max - X min . Обычно спектр регистрируется в +1-м порядке дифракции. Будем считать, что регист-

рирующая ПЗС-матрица расположена в плоскости z 0 при x ^E [ x min,1 , x max,1 ], где x min,1 R ^X min ^/ d и x _max ,1 = R X max / d — границы области спектра +1-го порядка дифракции.

Коррекция эффекта перекрытия порядков

Обозначим K = L X max / X min J , где L ’ J обозначает операцию взятия целой части. Из (12) получим, что x i ( X ) = x_K ( X / K ) . Поэтому при K >1 спектры порядков с номерами от +2 до K будут накладываться на область спектра +1-го порядка.

Покажем, что эффект наложения спектров может быть скорректирован за счёт простой обработки зарегистрированного изображения. Пусть S (X), X e [X min , X max ] -спектр излучения, падающего от щели. Именно этот спектр требуется восстановить по измерению интенсивности сигнала E ( x ), регистрируемого ПЗС-матрицей в области спектра +1-го порядка. При этом предполагается, что длины волн, не попавшие в указанный диапазон, отсекаются спектральным фильтром, расположенным либо на входе спектрометра, либо непосредственно перед ПЗС-матрицей. Согласно (9), (12), регистрируемая интенсивность имеет следующий вид:

S ( X ) 1 1 ( X ) ,

^{X E} [ ^X min , ^{2 X} min ) , x ^E L x min,1 , x m.2 ) ;

E (x ) = E (X) = <

^S ( ^X ) 1 1 ( ^X ) ^{+ S} I 2 ) ¹ 2 I "2 ) , ^{X E} [ ^{2 X} min , ^{3 X} min ) , x ^E L x min,2 , x min,3 ) ;

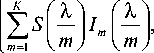
^{X E [} K ^X min , ^X max ^] , x ^E L x min, K , x max,1 J ^.

Из формулы (15) несложно видеть, что спектр падающего на решётку излучения может быть последовательно восстановлен по формуле:

Интенсивности порядков треугольной решётки несложно получить из (10), (13) в виде [2]:

S (X) =

I n ( X ) = sinc²

' E ( X ) ,

E ( X ) - S

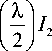
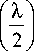
X E [ X min , 2 X min ) ;

XE [ 2 X min ,3 X min ) ;  ⁽¹⁶⁾

X 5

K

E ? ( X ) - I S |^X| I m Ц| , Xe [ K X min , X max ] • m = 2 I m )   I m )

Гиперспектральная аппаратура, используемая на спутниках дистанционного зондирования Земли, как правило, осуществляет наблюдение в диапазоне длин волн от X mi _n = 0,4 мкм до X _max=1,05 мкм [2,5,6]. В данном случае K =2, и поэтому при использовании схемы Оффнера возникает эффект перекрытия +1-го и +2-го порядков дифракции. Проиллюстрируем эффект перекрытия дифракционных порядков при следующих типичных геометрических параметрах: x 0 =25 мм, R =80 мм, d =30 мкм [1, 2, 5]. При указанных параметрах ширина спектра +1-го порядка составляет A x 1 = 1613 мкм.

В качестве дифракционной решётки обычно используется решётка с треугольным профилем [2]. Эйконал треугольной решётки определяется выражением

* gr ( x ) = X opt x / d , (17)

где X _opt - длина волны, на которой интенсивность +1-го порядка максимальна и равна единице. В последующих расчётах мы использовали значение X _opt = 0,640 мкм, выбранное из условия максимизации среднего значения интенсивности +1-го порядка дифракции в рассматриваемом диапазоне длин волн.

где sinc( x ) = sin( x ) / x . На рис. 2 показаны спектры +1-го и +2-го порядков дифракции треугольной решётки.

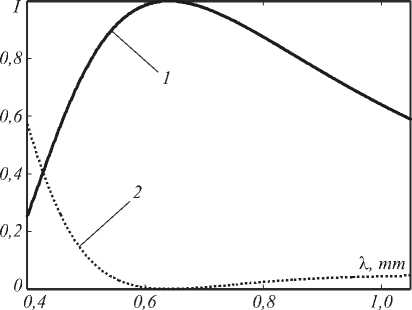
Рис. 2. Спектры дифракционных порядков с номерами +1 и +2 треугольной решётки, рассчитанной из условия максимума средней интенсивности в диапазоне [0,4-1,04] мкм

Эффект наложения порядков показан на рис. 3, где спектры +1-го и +2-го порядков приведены в зависимости от линейной координаты на ПЗС-матрице. Согласно (16), спектр падающего на решётку излучения может быть восстановлен по следующей формуле:

S (X)=ik

| E ? ( X ) ,                  XE [ X min ,2 X min ) ,         (19)

X I E? (X)- S ^2 j 12 ^22 j , XE[2Xmin, Xmax ], где In (X) имеет вид (18).

/ч.'гт

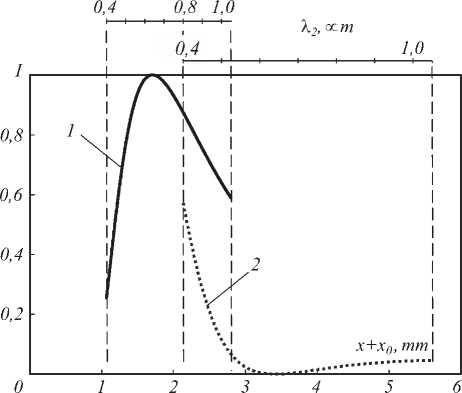
Рис. 3. Спектры дифракционных порядков с номерами +1 и +2 треугольной решётки в зависимости от линейной координаты на регистрирующей ПЗС-матрице

Отметим, что в общем непараксиальном случае зависимость x_n (λ) в порядках дифракции имеет более сложный вид по сравнению с (12). Точный расчёт положения спектров на регистрирующем устройстве может быть выполнен на основе результатов моделирования схемы спектрометра в одной из программ для расчёта оптических систем, например, в программе Zemax [9]. Для строгого описания взаимодействия излучения с дифракционной решёткой, расположенной на зеркале, может быть использован асимптотический метод из работы [7].

Заключение

Проведён анализ работы спектрометра Оффнера с дифракционной решёткой. Анализ проведён в параксиальном приближении и позволяет оценить положение спектров, формируемых в различных дифракционных порядках. Показана возможность коррекции негативного эффекта наложения спектров за счёт последовательной обработки зарегистрированного изображения (композиции спектров). При этом обработка сводится к поэлементному линейному преобразованию фрагментов зарегистрированного изображения. Для повышения точности коррекции расчёт границ положения спектров может быть выполнен на основе результатов моделирования схемы спектрометра в программе для расчёта оптических систем Zemax.

Работа выполнена за счёт гранта Российского научного фонда (РНФ) 14-31-00014.