О корректности модификаций формулы Байеса

Введение. Формула Байеса широко используется в теории вероятностей и статистике [1-9]. Весьма актуальным направлением применения формулы Байеса является разработка модификаций, обеспечивающих определение апостериорных условных вероятностей гипотез с учётом накапливания свидетельств.

Наиболее известны по крайней мере три различающиеся между собой модификации формулы Байеса, предназначенные для оценки апостериорных условных вероятностей гипотез с учётом накопленных свидетельств [2-4]. Две из них [3,4] являются модификациями формулы Байеса с изменениями, обеспечивающими учёт мультипликативно накопленных свидетельств, а одна [2] соответствует рекуррентному применению формулы Байеса с пошаговым получением соотношений, эквивалентных другой модификации [3].

Как показывает анализ, традиционно используемые модификации формулы Байеса, учитывающие мультипликативно накопленные свидетельства, не применимы для определения апостериорных условных вероятностей гипотез при мультипликативно накапливаемых свидетельствах, ввиду некорректности получаемых результатов.

Для устранения выявленного недостатка решается задача построения модификаций формулы Байеса, обеспечивающих учёт накапливаемых свидетельств с применением корректного нормирования.

Исходные положения. В основу излагаемых далее утверждений положим известное определение вероятности: «Чтобы количественно сравнивать между собой события по степени их возможности. очевидно, нужно с каждым событием связать определённое число, которое тем больше, чем более возможно событие. Такое число называется вероятностью события» [5].

Судя по приведённому определению, понятие вероятностей введено, в основном, для сравнения между собой различных событий по степени возможности, количественно выражаемой соотношениями измеренных значений их вероятностей.

С учётом сказанного целесообразно сформулировать представляющий объективную основу теории вероятностей, но не нашедший необходимого отражения в современной учебной и на-

Работа выполнена в рамках инициативной НИР.

учно-технической литературе принцип сохранения отношений изначальных вероятностей : корректная обработка вероятностей осуществима лишь при нормировании, выполненном с применением одного и того же нормирующего делителя, обеспечивающего равенство отношений нормированных вероятностей отношениям нормируемых изначальных априорных вероятностей.

Изначальные вероятности — вероятности, характеризующие степень возможности всех входящих в генеральную совокупность рассматриваемых событий или их комбинаций, совместно определённые априорно на основе объективных данных при условии учёта одних и тех же факторов.

Из сформулированного принципа следует, что:

отношения нормированных вероятностей событий или их комбинаций, образующих полную группу, в любых случаях получаются с использованием одного и того же нормирующего делителя и должны быть равны отношениям нормируемых изначальных вероятностей;

— сравнение и совместная обработка нормированных изначальных вероятностей событий или их комбинаций, принадлежащих разным полным группам, недопустимы, ввиду того, что такие вероятности получены с использованием разных нормирующих делителей.

При нарушении сформулированного принципа искажаются сведения о степени возможности рассматриваемых событий или их комбинаций, и получаемые на основе искажённых сведений результаты и принимаемые решения оказываются неадекватными реальным статистическим данным.

Следует исходить из того, что любые представляющие интерес для рассмотрения полные группы событий или их комбинаций выбираются из их генеральной совокупности субъективно. При этом в анализируемой предметной области (как в «дискретном куске действительности») рассматриваются только такие ситуации, при которых в результате опыта появляется хотя бы одно из событий или их комбинаций, входящих в выбираемую полную группу.

При определении условных вероятностей традиционно рассматриваются простые и комбинированные события.

• 1)    Простые (отдельно рассматриваемые) образуют полную группу {H_lzH₂,...,H_n} несовместных гипотез. При этом события характеризуются изначальными априорными вероятностями Р^), Р{Н₂}, ...,Р{Н_п}, сумма которых равна 1.

• 2)    Комбинированные — в виде мультипликативных комбинаций, представляемых произведениями Н_кЕ,,H_kE,Е^...,H_kE.Е,...E_m простых событий — учитываемых гипотез H_k(k = 1,...,п) и свидетельств Е^ = 1,...,ту подтверждающих гипотезы. При этом вероятности комбинаций событий определяются на основе предварительно полученных изначальных вероятностей — в частности, вероятность P(H_k Е_к ) комбинации простых событий Н_к и Е_г определяется как произведение известных изначальных априорных вероятностей Р^Н^ и Р^ЕДН^, так как Р^Н_кЕ^ = Р^НД P(E_l | НД согласно теореме умножения вероятностей [5].

Анализ известных соотношений. Как известно, формула Байеса [5] может быть записана в виде

. Р^НДР^НД

Р(Н_к 5)=---^V \ kj

ТДЧНДР^НД гдеР(А4) — априорная вероятность гипотезы (события-следствия) Нк(к = 1,...,п); Р^Е | НД — априорная условная вероятность наличия свидетельства (события-причины) Е при возникновении события-следствия Нк.

Нетрудно видеть, что выражением (1) представлена вероятностная доля Р(НДР(Е | НД среди всех возможных комбинаций Р(НДР(Е |НЛ), соответствующих к=1,...,п, указанных в знаменателе рассматриваемого соотношения в соответствии с так называемой [5] формулой полной вероятности Р^Е^ = у Р(Нк)Р(Е\ НЛ.

к=1                  1

Формула, использованная в публикации Нейлора [2], записывается в виде, более простом с точки зрения количества указываемых вычислительных операций:

.             Р(Нк)Р(Е\Нк)

Р(Н 5)=_____________ *__-__1 *___________ d Р(Нк)Р(Е\Нк) + Р(неНк)Р(Е\неНк)

где Р^Е | неН_к) — априорная вероятность наличия события-причины Епри невозникновении события-следствия Н_к.

В рамках традиционных допущений из формулы полной вероятности вида Р^Е | (Н_к + неН_к)) = Р(Н_к) Р^Е | И J + Р{неН_к) Р^Е | неН_к ) с учётом того, что при рассматриваемой полной группе несовместных гипотез неН_к = £ Я , следует, что

Р(Н J Р(Е \Н_к) + Р^неН,}Р{Е\ нен_к) = i Р(Н J Р(Е | Н_к).

Таким образом, соотношением (2) также представлена вероятностная доля Р(НДР(Е | Н_к^ среди указанных в знаменателе всевозможных комбинаций Р^Н^Р^Е | Н_к^, соответствующих к = 1,...,п, Другими словами, при традиционных допущениях в случае одного свидетельства Е как в знаменателях, так и в числителях обеих формул (1) и (2) представлены эквивалентные выражения.

Следует отметить, что в отличие от (1) в соотношении (2) используется значение Р^Е\неН_к^, которое при условии эквивалентности знаменателей может быть определено из уравнения:

£ Р(Нк )Р(Е\Нк) = Р(Нк) Р^Е \Нк) + Р(неНк)Р(Е\ неНк)

при этом

РЦДнеНк^

S Р^Р^Н?)  £ Р^Р^Н?)

i=Uj#k) ¹     _ i=Uj#k) ¹

Р1неНк^

^-Р{Нк}

В сущности, формула (2) была использована в публикации [2] как модификация формулы Байеса, весьма удобная для рекуррентных вычислений. Как отмечает автор публикации [2]*, в случае накапливания свидетельств, вычислив апостериорную вероятность гипотезы А^для одного учитываемого свидетельства Е, «мы забываем об этом, за исключением того, что априорная вероятность Р^ заменяется на Р(Н\ Е)», а затем продолжается выполнение вычислений, «но с учётом постоянной коррекции значения Р(Н) по мере поступления новой информации» (свидетельств).

В целях анализа корректности соотношений, традиционно применяемых для определения апостериорных условных вероятностей гипотез при накапливании свидетельств, вычислим с использованием формулы (2) апостериорные условные вероятности Р^ЕДН^ двух гипотез при каждом одном свидетельстве, а также вероятности Р^НДЕ^Е^ при двух свидетельствах на конкретном примере следующих исходных данных, характеризующих рассматриваемые значения априорных вероятностей:

Р^) = 0,3; Р(Е_г | HJ = 0,6; Р(Е₂ | HJ = 0,5;

Р^ = 0,7; Р(Е_г | На = 0,8; Р(Е₂ | Н₂) = 0,9.

С учётом исходных данных, запишем используемые далее промежуточные значения: РШ№1 | На = 0,18; Р(НаР(Е₂\ На = 0,15; Р(НаР(Е₂ 1 Н^Е, | HJ = 0,09; Р{Н₂}Р{Е, | Н₂) = 0,56; Р(НаР(Е₂ 1 Н₂) = 0,63; PIH₂W_X | НаР(Е₂ 1 На = 0,504;

I Р^аР^Д на = 0,74; 1 Р(НаР(Е₂\ На = 0,78; 1 Р^аР^ НаР(Е₂ \на = 0,594.

Для упрощения вычислений будем исходить из того, что значение Р^ЕДнеНа является вычисляемым, приводящим формулу (2) к соотношению, тождественно эквивалентному формуле (1) Байеса:

p(H\FA- р^нар^дна         р(нар(ЕДна _

• *' '' PW^EA^VPWW.XHeH^ ^ptHJPtE Дна

и, следовательно, при к= 1 Р(Н. I Еа = — = 0,243 и Р(Е. I На =    = 0,192,

111   0,74              11 г 0,78

при А-= 2 имеем P(w I Е)=^-= 0,757 и Р^НД Еа = ^-= 0,808.

• ^{21 1} 0,74                 ^{21 2} 0,78

Теперь определим апостериорную условную вероятность гипотезы ^ при двух свидетельствах с учётом того, что Ранена = 1 - Р(На и в формуле (5) в порядке её рекуррентного использования при к= 1 априорная вероятность Р(На заменяется на Р(Н_г | Еа:

.               р^нДЕар^ЕДна

Р(Н \Е Е ___________________ ^{11 1} __ ^{21 1} __________________.

12 р<^\Еар^дна+о--р(<нДЕашЕДнена

Подстановка вычисляемого в соответствии с (4) значения

Р^ЕДнеНа =

2                                ,

^i/^'^²^ рднардЕДна

£ р^а

/=ц/#1)

р^на

^р^дна-оа,

приводит к принимающему соответствующее значение соотношению р^наридна    .

2              . ^rV^L2 V ‘V

Р(Н, \E.Ea =_______________ р(н аридна

yp{h аридна

2                                 , учнаридна

р(е₂ \на +ci -               _W2 |н₂)

^наридна

₌ р^нар^д народна ₌ 0,09 _{= 0152} 1р(нар(ЕДнар(ЕДна °'⁵⁹⁴ ' ‘

„            . р^нар^ЕДнародна 0504

Аналогично Р(Н, Е,Еа= ,          ^{1        1}      =      = 0,848.

ур^нар^ЕДнародна °'594

Следует обратить внимание на то, что формула (2) в случае учёта m свидетельств приводит к довольно известной (см., например, [3, с. 284-285]) модификации формулы Байеса

РУкЖЕД НкЖЕД НкЖ.хРЖ\ HJ

учитывающей множество накопленных свидетельств.

Из анализа результатов, полученных при каждом из двух рассматриваемых свидетельств и при их мультипликативной комбинации, имеем два следствия.

Во-первых, при традиционно применяемых методах вычисления апостериорных условных вероятностей Р^Н_Х | fj , Р^Н_Х | f₂) и Р^Н_Х 1^^) осуществляются с использованием разных нормирующих делителей, что исключает возможность их сравнения и совместной обработки.

Во-вторых, при мультипликативном накапливании свидетельств отсутствует мультипликативный эффект:

• —    апостериорная условная вероятность гипотезы Hi, равная при одном свидетельстве Р^Н_Х | 5J = 0,243 либо Р^Н_Х | f₂) = 0,192, при переходе к двум свидетельствам уменьшилась до Р^НДЕ.Е^ = 0,152,

• —    апостериорная условная вероятность гипотезы Hi, равная при одном свидетельстве Р(Н₂ 1 5J = 0,757 либо Р(Н₂ 1 f₂) = 0,808, при переходе к двум свидетельствам увеличилась до Р(Н₂\Е_хЕД = 0,848.

Заключая сказанное, следует также отметить, что использование разных нормирующих делителей при изменяющемся количестве учитываемых свидетельств и несоблюдение мультипликативного эффекта присуще не только модификациям формулы Байеса (2) и (6), но и другой модификации, имеющей [4] следующий вид:

|СС О ^ Р(НкЖЕх\НкЖЕДНкЕху...• Р^Ет\НкЕхЕ2 •-Ет^ г\пк | с1с1—ст) - „                                                      ■

Е Р(Н_кЖЕ_х | Н_кЖЕ₂ 1 Н_кЕ^ •.... Р(Е_т \Н_кЕ_х Е, •.... E_mJ

Таким образом, традиционные методы оценки апостериорных условных вероятностей гипотез, учитывающие накапливание свидетельств, ввиду того, что при нормировании таких вероятностей используются разные нормирующие делители, приводят к некорректным результатам: при мультипликативном накапливании свидетельств уменьшение апостериорных условных вероятностей каждой из гипотез (связанное с мультипликативным эффектом, соответствующим теоретико-вероятностным закономерностям) оказывается неосуществимым.

Следует также обратить внимание на то, что с применением известных модификаций формулы Байеса оцениваются апостериорные условные вероятности гипотез при свидетельствах, накопленных в порядке их предварительно установленной нумерации, в то время как более реальными являются случаи, когда порядок поступления свидетельств является изменяемым. Это можно учесть при построении модификаций формулы Байеса с корректным нормированием. Нетрадиционное нормирование. Сравнение апостериорных условных вероятностей гипотез при неодинаковом (изменяемом) количестве свидетельств осуществимо в случае корректного нормирования с использованием не разных нормирующих делителей, а одного общего делителя q, равного сумме альтернативных выражений, указанных в числителях всех используемых соотношений, а следовательно, и сумме всех ранее использованных нормирующих делителей.

Например, в случае рассмотренных априорных исходных данных, ввиду того, что нормируемыми являются вероятности Р(НкЖЕ,|Н^, i=l или /=2, и Р^НДЖЕДНДЖЕДНД), к= 1,...,2, нормирующий делитель выбирается равным q = Z Р{Нк)Р{Е, \Нк} + 1 Р{НкЖЕ2 \Нк)+1 Р{НкЖЕ1 | НкЖЕг \Нк).

Можно перейти к более простой записи нормирующего делителя. Если просуммировать слагаемые с сомножителями, представляющими вероятности альтернативных комбинаций свидетельств при гипотезе Hi, и раздельно просуммировать аналогичные слагаемые с вероятностями при гипотезе Hi с вынесением одинаковых сомножителей Р(Н_к) за скобки, и затем полученные выражения сложить, то (при п = m = 2)

q = I^HJYP^ | HJ + P(E. \на + P^ | H_kWi | O) =

= Z №)[l Р^Е, I H_k) + п Р(Е, | Н_к )1 и V L'=i              /=1            А)

С использованием общего нормирующего делителя, который при заданных конкретных исходных данных принимает значение q = 0,74+0,78+0,594 = 2,114, равное сумме ранее использованных знаменателей, естественно, получаем иные результаты:

Р(Н |е) = -21И= о,О85,

V        2д14    '   ,

= 0,043;

• ^{1    2 7} 2,114

Р(Н_?\Е_?) = ^- = 0,298;

v 2,114

Результаты вычислений, выполненных для

PWx\E7V

pw7\ex^

0,15 2,114 0,56 2,114

= 0,071;

= 0,265;

Р^НЛЕ. Е₇)= 21521 = 0,238.

• ^{21 1 2 7} 2,114

рассматриваемого примера конкретных апри-

орных исходных данных, подтверждают, что в случае нетрадиционного (корректного) нормирования значения апостериорных условных вероятностей всех гипотез при мультипликативном учёте накапливаемых свидетельств могут только уменьшаться, что соответствует теоретико-вероятностным закономерностям. В частности, при заданных априорных исходных данных конкретно рассматриваемого примера апостериорные условные вероятности обеих гипотез при получении второго свидетельства (ввиду мультипликативного эффекта) уменьшились: апостериорная условная вероятность гипотезы Hi уменьшилась с 0,085 либо с 0,071 до 0,043, а прежде увеличившаяся вероятность гипотезы Hi уменьшилась с 0,265 либо с 0,298 до 0,238.

Таким образом, на основе обобщения (7) может быть предложено корректное соотношение для определения апостериорных условных вероятностей гипотез в случае изменяемого количества р = 1,...,/77 мультипликативно накапливаемых свидетельств:

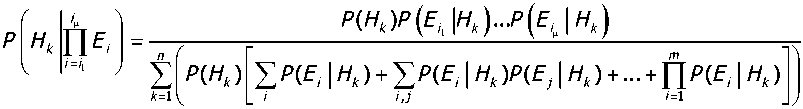
где Е_к — первое поступившее свидетельство, ..., E_t — ц-е поступившее свидетельство, причём (е, ...еД^Е.—Е V и ввиду того, что множество ^...еД является подмножеством ^Fp.^j, учитывается произвольный порядок поступления свидетельств.

Соответствующая записанному соотношению рекуррентная формула при начальном значении

Р^нДе^

р^^деднд

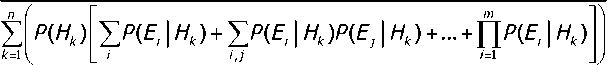
имеет вид:

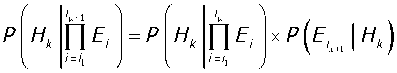
Такая формула в отличие от прототипов, ввиду корректного нормирования, является существенно более адекватной изначальным статистическим данным. При этом в каждом шаге рекуррентного процесса используется всего одна расчётная операция умножения.

Заключение. Известные модификации формулы Байеса, используемые для вычисления апостериорных условных вероятностей несовместных гипотез с учётом того или иного количества мультипликативно накопленных свидетельств, не применимы для определения апостериорных условных вероятностей, учитывающих изменяемое количество последовательно накапливаемых свидетельств, так как, ввиду неодинакового нормирования, приводят к результатам, не соответствующим теоретико-вероятностным закономерностям. Сравнение апостериорных условных вероятностей гипотез при изменяемом количестве свидетельств осуществимо в случае корректного нормирования с использованием не разных нормирующих делителей, а одного общего делителя, равного сумме значений тех нормируемых вероятностей, которые подлежат сравнению либо совместной обработке.