О краевой задаче Римана для функций многих комплексных переменных, голоморфных в кратнокруговых областях $\ bbb C^n $

Теория краевых задач для аналитических функций одного комплексного переменного ([3, И]) нашла многочисленные применения как в самой математике (сингулярные интегральные уравнения, уравнения типа свертки и др.), так и в решении прикладных вопросов (в теории упругости, гидроаэродинамике, теории переноса частиц, теории массового обслуживания и т. д.). При решении одномерных краевых задач основным математическим аппаратом является интеграл типа Коши.

Начиная с середины XX века сильно возрос интерес к теории функций многих комплексных переменных. Эта теория в работах научных школ академиков Н. Н. Боголюбова, В. С. Владимирова, Ю. В. Линника получила эффективные приложения в квантовой теории поля [2] и математической статистике [6]. В последние годы описан широкий класс задач квантовой механики, теории вероятностей, математической физики, которые соответствующим преобразованием Фурье приводятся к многомерным краевым задачам линейного сопряжения (пространственной задаче Римана).

Установленные А. А. Темляковым в 1954 году интегральные представления голоморфных функций для ограниченных выпуклых полных двоякокруговых областей и развитый на их базе математический аппарат интегралов типа Темлякова (см., например, [4, 18]) явились той основой, на которой Г. Л. Луканкин (см., например, [7-9]) и его ученики (В. И. Боганов, И. Н. Виноградова, X. П. Дзебисов, С. Ю. Колягин и др.) начали исследования по разработке теории краевых задач линейного сопряжения функций двух комплексных переменных, голоморфных в двоякокруговых областях.

Параллельно велись работы по распространению интегральных представлений Темлякова в пространство С” (п > 2). На этом пути польские математики 3. Опи-ал и Ё. Сичак [19] получили интегральную формулу (п-мерный аналог интегралов Темлякова) для введенного ими класса ограниченных выпуклых полных п-круговых областей типа (Т). И. И. Баврин (см. [1]) с помощью созданного им метода интегро-дифференциальных операторов голоморфных функций установил для этих областей ряд интегральных представлений более общей природы.

Автором, с помощью развиваемого метода линейных дифференциальных операторов с переменными коэффициентами (см. [13]), были исследованы [12] интегралы типа Темлякова и Темлякова — Баврина с определяющими областями D Е (Т).

В настоящей статье продолжена разработка математического аппарата интеграла типа Темлякова I рода с определяющей n-круговой (п > 2) областью D типа А. Этот аппарат применяется для постановки и решения однородной и неоднородной задач линейного сопряжения в С”.

§1. Исследование поведения интеграла типа Темлякова I рода с определяющей областью D Е (Т) типа А

Важным подклассом областей типа (Т) являются области D типа А'.

D = {г ЕС" : cil^il 4----- V c_n\z_n\ < 1, щ,... ,с_п > 0}.

Рассмотрим интеграл типа Темлякова I рода с определяющей областью D типа А:

РИ = _2_[м[^д [

^=1

где к = щ^! + с2г2е-гб2 4----+ спгпе~гвп.

9 = (9₂,... ,9_п), 0 <  0j < 2%, j = 2,п, т = (т_ь ... ,т„) Е А, А — (п — 1)-мерный симплекс, т. е.

А = {т : Ti 4-----4 т„ = 1, т_х > 0,... , т_п > 0}

= {т : т_х = 1 - т₂----- _Тп1 ^... ,т_п) Е А*},

А* = {(т2,..., т„) : 0 < т2 < 1, 0 < т3 < 1 - т2,... , 0 < т„ < 1 - т2

т„-1},

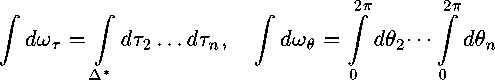
и окружность г/ = 1 ориентирована как обычно в положительном направлении.

Будем предполагать, что плотность интеграла (2) f^T,9,i^ есть функция класса ц (J^T,9,Tf^, т. е. определена и непрерывна по совокупности аргументов на множестве

М = {(т, 0,ц) : т Е А, 0 ^ 9j ^ 2тг, г/ = 1,7 = 2,п}

2тг-периодична по 9j, j = 2,п, и удовлетворяет по г/ условию Гёльдера Н_а (0 < а > 1), а именно

^т.е,^- fVT191O 0 и а не зависят от т и 9. Учитывая, что ядро интеграла (2) не зависит от т, условимся далее рассматривать этот интеграл в виде

РИ = _1_иб [ -£!Ма,, х ' (2тг)иг J J i]-u

I’vH1

где ^(0,7/) = //(тДд/) dw_T.

Как было установлено в [12], определяемые интегралом (3) функции являются голоморфными в области Рив неограниченных областях

Е„ = {г 6 С" : сМ\ " С1Ы-----с_₁|^_₁| - с,₊₁|^₊₁|----- c_u\z_u\> 1},   (4)

v = 1,п, неголоморфными, вообще говоря, в C"\(D U Si U • • • U S„) и непрерывными во всем пространстве С”, за исключением расположенных на соответствующих координатных плоскостях окружностей

В„ = ^еС : г = (0,... , 0, ^, 0,... , 0), \z_v\ = с"¹}, v = 1ДГ, (5)

называемых окру леностями особенностей интеграла (3) (легко видеть, что в их точках тождественно по всем 0j выполняется равенство u = 1).

Внутренний интеграл в (3) (по г/) будем в дальнейшем понимать как особый (сингулярный) в смысле главного значения по Коши.

Отметим, что сопряжение области D с каждой из областей E_v происходит по соответствующей окружности B_V1 v = Eri.

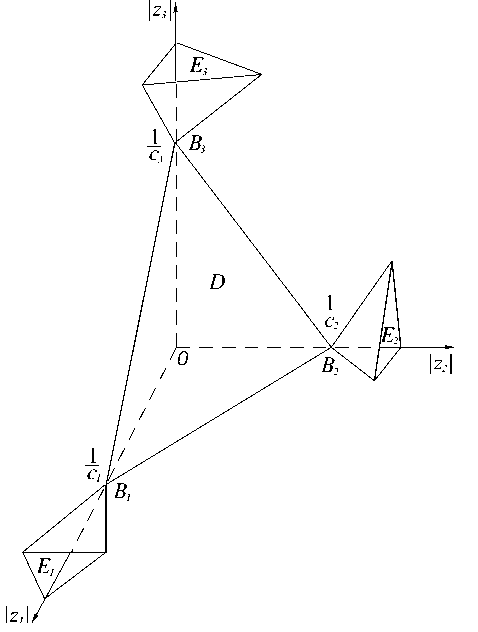
Для случая пространства трех комплексных переменных С3 расположение образов областей Si,S2 и S3 в «абсолютном октанте» проиллюстрировано на рис. 1.

|z3 | E3 c 1 3 B3 /1 \ D 0 / / / / / / 1 c1 B1 / / / E1 z '                       Рис.1. Введем обозначение 1 Г ^Md = Г Ф+(0^): 2тп J т] — и       1 Ф- (0, и), Ы = 1

1 c2    E B2               |z2 | если и < 1, если и > 1,

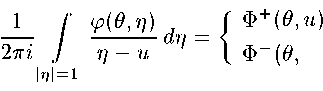
и будем называть функции Ф⁺(Д и) и Ф^-(0, и) определяющими функциями интеграла типа Темлякова I рода (3).

Учитывая, что всюду в области D тождественно по всем 0j выполняется неравенство a < 1, а в областях E_v ^v = 1,п) — неравенство u > 1, заключаем, что в D справедлива формула

W = — [ Ф⁺(Дн)М,               (6)

а в E_v — формула

W =   *   [ ф"^,^аШ9.                  (?)

Без ограничения общности рассуждений, далее для определенности будем считать и = 1 и коэффициент щ = 1 (к области типа А общего вида легко перейти элементарным преобразованием подобия). Пусть точка Д = (r/i,0,... , 0) Е В^. Обозначим

^⁺(Д) = lim Е^, Е"^= lim F(z), м_х = а _. = щ.

z—>zi                       z—>zi                    z —zi z£D                  z£Ei

Теорема 1. Если функция р^0,т^ такова, что интеграл J v’^^ dr] имеет рав- постепенно абсолютно непрерывные (п — 1)-кратные интегралы по 9 у у = 2,п, и сингулярный интеграл ^7 f ^v^^ dr] (|ai = 1) существует почти всюду на окружности \л\ = 1

особенностей В^, то интеграл типа Темлякова I рода почти всюду на В^ имеет конечные пределвные значения из областей D и Е^, вычисляемые по формулам f+^ = tA^ /Аше / ^^^ + 7Т^т / ^е^Шв1 (8) (2тг)пг J J 1] - щ (2л)" 1 J

Ы = 1

^F"^ = -^(da)_e [ ^^dr]-—^ [р^щИ^ (9) (2л)"г J J 1] - тц (2л)" ¹ J

И = 1

причем эти значения не зависят от пути приближения точки z к z^ Е By.

• <    Доказательство теоремы основано на формулах Сохоцкого для определяющих функций:

lim Ф+(Д и) = Ф+(0, гр) = —dr] +

Z->Z1                              2тп J 7] — Г]12

ZGD                                 1^1 = 1

lim Ф (0,н) = Ф (Уд/1) = тДт /         dr] —      г/1). > z^ii                             2тп J 7] — Г/1

zGEi                                   |^| = i

Теорема 2. Пределвные значения интеграла типа Темлякова I рода (3) из областей D и Ei в точках окружностей В^ удовлетворяют условию Гёльдера Н\, причем А = а, если 0 < а < 1, и А = 1 — о, если а = 1, где о — сколь угодно малое положи-телвное число.

• <    Доказательство теоремы сводится к проверке выполнимости для любой пары точек z'^ = (гф 0,... , 0), Д' = (Д', 0,... , 0) G Bi неравенств

|в+(Д)-в⁺(Д') <к\_ч'_х-_ч';\\                   (ю)

\f-^-f-^\<<-<. ▻           (и)

Рассмотрим теперь вопрос о поведении интеграла (3) на множестве бесконечно удаленных точек пространства С (это множество состоит из точек (zi,..., z_n), у которых хотя бы одна координата равна оо) при стремлении к ним из области Е^.

Пусть р > 1 — произвольное положительное число. Тогда для области

Е1,р = {z ECn : |^i - c2\z2\-----cn\zn \ > р} тождественно по всем Ор] = 2,п, выполняется неравенство и > р. Следовательно, если z G EiiP, то

• ^М= (^т/^(».")^«.              (12)

где Ф" (0, и) = ^ ^, _{= 1} ^ ^d^ hl >  Р-

Далее, пусть точка z стремиться к бесконечно удаленной точке из области Ei_iP (понятно, что это не может быть точка, у которой ограничена первая координата) и р ^ р₀ = | + 1, где б — сколь угодно малое положительное число, с = sup {|Д0, г/) : 0 ^ 0j ^ 2тг, j = 2,п, г/ = 1}. Тогда Ф”(0,и) <  б и, следовательно,

IWm / ^^(h^l^^T^^T / d^=§.     (13)

(2тг)^{п 1} J ¹                  (2тг)^{п 1} J

Полученное неравенство показывает, что в бесконечно удаленных точках при стремлении к ним произвольным способом из области Ец_р интеграл типа Темлякова I рода (3) обращается в нуль.

Определение 1. Будем говорить, что функция /(г) есть функция класса (Т), если она:

• 1)    непрерывна во всем пространстве С^п за исключением точек окружностей B_v ^ = 1,™);

• 2)    голоморфна в D U Ei U • • • U Ер

• 3)    неголоморфна, вообще говоря, в Cⁿ\(D U Ei U • • • U Е_п)-

• 4)    /(г) имеет конечные предельные значения в точках окружностей B_v при стремлении точки z к z_v = (0,... , 0, с”¹^^, 0,... , 0) Е B_v ^\ц_р\ = 1) из D и E_v.

Следствие 1. Всякая функция, определяемая интегралом типа Темлякова I рода (3) принадлежит классу (Т).

• §2 . Постановка и решение однородной задачи линейного сопряжения в классе функций (Т)

Постановка задачи. Пусть в пространстве С” задана область D типа А'.

D = {г G С" : \z_T \ + c₂\z₂\ А -----h с„ z„ < 1, с₂ > 0,... , с_п > 0}.

Требуется найти функцию / (г) класса (Т), исчезающую в бесконечно удаленных точках при стремлении к ним из области Ei, удовлетворяющую в точках окружности Bi = {г Е С” : z = zi = (щ, 0 ... , 0), щ = 1} краевому условию

Л^СЫ/"1^),

где

/ Л1) = hm /(г), / (zj = hm /(г), zED                 z£Ei а функция G^]i) определена на окружности В^, нигде на ней не обращается в нуль и удовлетворяет условию Гёльдера, причем ее индекс х = IndG(r/i) > 0.

Решение. Учитывая, что функции, определяемые интегралом типа Темлякова I рода (3), являются функциями класса (Т) будем искать решение задачи в виде интеграла (3). Подставляя в соотношение (14) предельные значения интеграла (3), выраженные по формулам (8) и (9), получим

--^— /dwg / ^^'^ ^ +  ^ Г ^q^dwe

(2тг)^иг J J q- qi (2тг)^{п 1} J

^=1

= Л/х) •

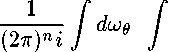
^^- dq -   ^   [ tp^ q^dwg

i] - q_x (2%)" ¹ J

ИЛИ

2                        I M^)J^ _{= 0}

2 • (2%)" J V                                ггг J q — qi

Ы=1

Отсюда следует, что

I ^t^^Ldq = W₁q_iy       (15)

th J q - qi

Vn\=l где функция A(0,r/i), предполагаемая непрерывной по совокупности аргументов и удовлетворяющей по щ условию Гёльдера, независимому от 9^ j = 2,п, является решением уравнения J X^qi] dug = 0, а коэффициент 2 в правой части взят для удобства дальнейших выкладок.

Решать полученное сингулярное интегральное уравнение с ядром Коши (15) будем тем же способом, каким решают характеристическое уравнение в теории функций одного комплексного переменного (см. [3, §21]). Рассмотрим с этой целью интеграл типа Коши

f тАРЩ                   (16)

2тп J 7] — и

|7?| = 1

где и = Z! Е c₂z₂e ^г6- А----+ c_nz_ne ^г8п

Учитывая равенство Рпц.^ u = ?ц и используя формулы Сохоцкого для интеграла (16), перепишем уравнение (15) в виде

<Ж,т/1) + С(?/х) • У?(0,7/1) + 2Ф+(0,7/Х) - <^(0,7/1)

- СЫ • F^T]^ " 2G(t/i) ■ Ф-(0,/,1) = 2А(0,7/х), или, что тоже самое,

Ф+(Ж) = С(7/1).ф"(0,7/1) + А(0,7/1).

Таким образом, решение сингулярного интегрального уравнения (15) (а значит и поставленной однородной задачи линейного сопряжения) свелось к решению задачи Римана с краевым условием (17). Решение этой задачи, учитывая, что х > О, имеет вид

Х^ Г Х^Од])

7?| =

dp

т) — и

+ Х(и) • Px_i^u^

где ег+("),         если u < 1, гМ = 2- I 'XiEXM^

Ркг J ц — и Ы=1

и^-х • е^г W, если u > 1,

Р_И-1И — полином степени не выше х — 1 с произвольными комлексными переменными (при х = 1 Р_И-1^ = Со; при х = 0 полагаем Р_И_1^ = 0).

Итак, найдены определяющие функции Ф^±(0,и) интеграла (3). Далее, используя формулу (18), по формулам (6) и (7) (последняя записана относительно Еф) получаем решение поставленной задачи.

ЗАМЕЧАНИЕ 1. Вычислив с помощью формул Сохоцкого предельные значения определяющих функций, можно найти плотность интеграла типа Темлякова I рода (р^Од^, где y(0,7/i) = Ф⁺(0,r/i) — Ф“ (0,7/1), а значит по формуле (3) и решение поставленной однородной задачи линейного сопряжения.

ЗАМЕЧАНИЕ 2. Наличие в найденном решении задачи полинома Р_И_1^ с произвольными коэффициентами и некоторой неизвестной функции А(0, ?/) указывают на неоднозначность решения. Решение задачи станет вполне определенным, если наложить на искомую функцию С⁺(г) = F^ (или F^-^ = F^) х независимых условий.

z£D z£Ei

Например, это можно сделать следующим образом: задать в начале координат (где 77 = 0) значение определяющей функции Ф⁺(0,и) и всех ее производных по и до порядка х — 1 включительно. Это позволит найти коэффициенты полинома P^_i(tz).

Найдем, например, коэффициент Со- Пусть задано значение Ф+(0, u) |и_0 = Ф+(0,О). Из формулы (18) следует, что

Ф⁺(О) _ 1 Г W _{+ г}

Х+(0) 2тп J Х+^ 7/    ¹

177| = 1

Интегрируя данное соотношение по 9^ 7 = 2, п, в пределах от 0 до 2тг и учитывая, что

J А (0, г/) dwg = 0, получаем

1 Г Ф⁺(О) , (27г)"-¹ J Х+(0)

Vz^^ b^-^

ИЛИ

F+(0) ^W

так как F⁺(0) = ^Vi J Ф⁺(0, 0) dwg.

Далее, для нахождения функции А(0,г/) надо решать уравнение (19), в котором Со определяется по формуле (20).

• §3 . Постановка и решение неоднородной задачи линейного сопряжения в классе функций (Т)

Постановка задачи. Пусть в пространстве С” задана область D типа А. Требуется найти функцию /(г) класса (Т), исчезающую в бесконечно удаленных точках при стремлении к ним из области Е^ и удовлетворяющую в точках окружности В^ краевому условию

/+(Д) = С(щ)/-(Д)+д(щ),                    (21)

где функции G^q^ и g(r/i) определены и удовлетворяют условию Гёльдера на окружности В^, причем G^q^ нигде на В^ не обращается в нуль.

Решение. Будем искать решение задачи в виде интеграла типа Темлякова I рода (3). Подставляя формулы предельных значений этого интеграла (8) и (9) в краевое условие (21), получаем

—Д— f dwg I ^^е,Т1^ d-q +   ¹ f tp^^^dwg

(2тг)^пг J J 9 - 91 (2тг)^{п 1} J

Ы = 1

ИЛИ

= G^ •

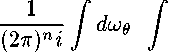
^^- d-q -       / p^ ib dwg

9 - q_x (2?r)^{n 1} J

+ gbb

, .„V, / [u₊^g^ • ■^’и)+¹ °^ы /

17/| = l

P ^Pl) ,     ₉ , X

-------dq - 2g(r/i) 9 - 91

dwg = 0.

Отсюда следует, что

(1 + О(7_/1))^(Дщ) + ^— ^M [ ^Ldq иг J q - qi

\g\ = l

= 2(g(r/1) + A1(0,r/1)),      (22)

где Ai(0,r/i) — некоторая функция, предполагаемая непрерывной по совокупности аргументов и удовлетворяющей по qi условию Гёльдера, независимому от 9, является решением уравнения J Ai(0,r/i) dwg = 0.

Полученное уравнение (22) есть сингулярное интегральное уравнение с ядром Коши, решать которое будем тем же способом, каким решают характеристическое уравнение в теории функций одного комплексного переменного ([3, §21]). Рассмотрим с этой целью интеграл типа Коши (16). Учитывая равенство lim и = тц и используя формулы Сохоцкого для интеграла (16), перепишем уравнение (22) в виде

^(0,01) + G(7)i)^(0,7?i) + 2Ф⁺(0, 7/1) - Д0,7/1)

- 6'(7/1))(0,7/1) - 2С'(7/1)Ф" (0,7/1) = 2(д(?/1) + А1 (0, 7/1))

или

Ф⁺(0,7/1) = СД/^Ф (0,7/1) + Дщ) + Ai(0,7/i).

Решение сингулярного интегрального уравнения (22), а значит и поставленной неоднородной задачи линейного сопряжения, свелось, таким образом, к решению задачи Римана с краевым условием (23).

Рассмотрим два возможных случая.

• 1)    Пусть х = JndG(7/i) > 0. Тогда решение задачи имеет вид

Ф(6,„) = АМ [                +

^{V ;} 2тп J У+(7/)      7/ -и ^{V И h}

Ы = 1

где

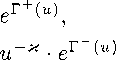
если u < 1, если u > 1,

ГЫ = ф [ МТ* • 0(^)1 д,.

2тп J ц — и Ы = 1

Р_Х-1М — полином степени не выше х — 1 с произвольными комплексными коэффициентами (при х = 0 полагаем Р_И_1Н = 0).

• 2)    Пусть х = JndG(7/i) < 0. Тогда решение задачи имеет вид

хн Г gW + ^1(0,0) . dg

2ivi J X+H 7/ — и

Ы = 1

Отметим следующее обстоятельство. Неоднородная задача Римана в случае х <  — 1, вообще говоря, неразрешима. Для ее разрешимости необходимо и достаточно, чтобы выполнялись следующие х| условий:

/ ^ДД’ -у-^-о. *=1.2.....и.

Ы = 1

Итак, найдены определяющие функции Ф⁺(0,и) и Ф^-(0,и), задаваемые формулой (24), если х > О, или формулой (25), если х < 0. Подставляя их в формулы (6) и (7) получим решение поставленной задачи.

Замечание 3. Решение поставленной неоднородной краевой задачи можно найти в виде интеграла типа Темлякова I рода (3) с плотностью ip^g), где y(0,r/i) = Ф⁺(0,г/1) — Ф^-(0,г/1), а Ф⁺(0,г/1) и Ф"(0,г/_х) есть предельные значения определяющих функций, вычисленные по формулам Сохоцкого.

Замечание 4. Если для нахождения решения краевой задачи используется формула (24), то решение зависит от полинома Р_и_1^ с произвольными комплексными коэффициентами и некоторой неизвестной функции Ai(0,r/). Решение задачи станет вполне определенным, если наложить на искомую функцию F⁺^ (или F~ (г)) х независимых условий. Это, например, можно сделать так: задать в начале координат (где и = 0) значение определяющей функции Ф⁺(0,и) и всех ее производных по и до порядка х — 1 включительно. Это позволит найти коэффициенты полинома P_x_i^nY

Найдем, например, коэффициент Со Пусть задано значение Ф⁺(0,и)|_и__о = Ф⁺(0,О). Из формулы (24) следует, что

Ф⁺ (6», 0) ₌ 1 Г д^д) + A_x(0,r/) dg ~

Х+(0) 2тп J Х+^    ' г/ *

Ы = 1

Интегрируя это соотношение по 9^ j = 2,п, в пределах от 0 до 2% и учитывая, что J Ai(0,r/i) dwg = 0, получаем

1 Г / ф+ (0,0)    1 Г д^ dg

(27г)»-¹ J I Х+(0) ” 2^" У          7

Ы=1

т. е.

₌ F⁺(0)    1 Г д^) dg

°   Х+(0)   2тп У Х+^ ' г/ ’

M=i поскольку

^+(0) =        / Ф+(0,О)М.

(2тг<)^{п 1} J

Подставив значение коэффициента Со в соотношение (26), получаем уравнение для нахождения функции Ai(0,r/):

1 Г Х^блЙ dg Ф⁺(0,О)-F⁺(0)

2^7 J Х+^ ' V “    Х+(0)    '

Ы = 1

Если же решение краевой задачи находится с использованием формулы (25) (т. е. индекс х < 0), то это решение будет содержать неизвестную функцию Ai(0, г/). В этом случае для получения определенного решения надо на функцию F*^ (или F“(^)) наложить одно условие. Например, так же, как в рассмотренном случае, можно задать в начале координат (где и = 0) значение определяющей функции Ф⁺(0,О). Тогда для нахождения функции Ai(0,r/) следует рассмотреть уравнение

Следствие 2. В случае G^i) = 1 неоднородная задача линейного сопряжения обращается в задачу о скачке с краевым условием

/⁺(я) - /"(^1) = эЫ-

• §4. Прибавление

Отметим, что краевые задачи линейного сопряжения, близкие по постановке к рассмотренным выше, но решение которых ищется в классах функций, определяемых различными интегралами типа Темлякова — Барвина, были изучены в совместных работах автора и его учеников.

Так, в совместном с А. Е. Луковниковым исследовании 2000 года [15], получившем дальнейшее развитие в его диссертационной работе [10], были рассмотрены однородная и неоднородная задачи, в которых решение искалось в классе интегралов типа Темлякова — Барвина I рода первого порядка

* Ьлаш, г ^^            (27)

О          М = 1

где u = ci^i + c^ez^e^-1®- + • • • + c_nez_ne~^l9n.

В работах, написанных в соавторстве с А. С. Якшиной (см., например, [16]), подобные задачи были рассмотрены и решены в классе функций, определяемых интегралом вида (27), но в котором u = и^^) = с^е⁸¹ z-v + с^е⁸- z^e^-16- + • • • + c_ne⁸" z_ne~^lSn , где показатели 51,... , 5_П представляют собой набор из нулей и единиц, причем нулю равны 5_Р1,... , 5„_к (щ < z/₂< • • • < Щ, 2 <  k < п — 1), а единице — все остальные показатели.

Отметим, наконец, что автором в 2001-2002 годах произведена постановка и указано решение соответствующих краевых задач в классах функций, определяемых интегралом типа Темлякова I рода с более широким, чем n-круговые определяющие области D типа А, классом круговых определяющих областей.