О краевых задачах электродинамики без калибровки Лоренца

Одним из наиболее широко используемых в прикладной электродинамике прямых вариационных методов является метод Галеркина [1]. Обычно в нем в качестве нулевого элемента функционального пространства, определяемого

Выражения:

-                д JA    -   1     -

Е = - grad ф--; H = — rotA д t         ц

приводят к соотношениям, устанавливающим

операторным уравнением, задается уравнение Гельмгольца, к которому приводят уравнения Максвелла при использовании калибровки Ло-

связь между компонентами электрического и

магнитного полей:

Е — = - rot rot П ^e

ренца:

дггг

- ц rot--- д t

- дф div A = -бц   , д t ,

H — = rot rot П ^m

дй ^e

+ б rot----. д t

где ф и A — скалярный и векторный потенциалы электромагнитного поля. Действительно, следствием соотношения (1) являются волновые

Таким образом, калибровка Лоренца устанав-

уравнения:

^{д ф    р}    _А ^{-      д} A    -

\ф бц         ; Д А -бц —5- = -ц j ,       (2)

д t ²       б              д t

где р и j — плотности объемных свободных за-

рядов и токов.

При гармонической временной зависимости уравнения (2) приводят к уравнениям Гельмгольца. Выражая скалярный и векторный потенциалы через векторы Герца П ^e ’ ^m :

-      -       дП e     л          - ф = -div Пe ; A = бц ; A = ц rot Пm , д t

приходим к волновым уравнениям

ДП ^e , ^m

-

д2П e,m бц---5— д 11'

*          *

^Р Г м ^б I ц

где Р — и M f — векторы поляризации и намагничивания, определяющие функции источников электромагнитного поля.

ливает связь между компонентами электромагнитного поля в виде (4).

В том случае, когда условие (1) на электромагнитное поле не накладывается, операторная связь (3), (4) полей отсутствует, в результате чего в качестве нулевого элемента функционального пространства может фигурировать непосредственно система уравнений Максвелла, а компоненты электрического и магнитного полей в силу отсутствия их аналитической связи вида (4) допускают автономные разложения по произвольным ортогональным базисам. Связь между компонентами в дальнейшем может быть установлена, например, с помощью процедуры Галеркина, применяемой к уравнениям Максвелла. Такой подход расширяет возможности прямых вариационных методов. Продемонстрируем схему его применения на конкретном примере.

Рассмотрим прямоугольный волновод с диэлектрическим заполнением, регулярным по © С.Б. Раевский, А.Ю. Седаков, А.А. Титаренко, 2014

продольной координате z и произвольным по поперечным координатам (рис. 1), причем значения диэлектрических проницаемостей могут быть и комплексными величинами.

Представив диэлектрическое заполнение в прямоугольном волноводе кусочно-непрерывной функцией, запишем уравнения Максвелла для всей области внутри рассматриваемого волновода:

rot ( E ) = - i юц о H H , rot ( H ) = i toe ( x, y ) 8 0 E .

Из уравнений (5) получаем:

rot rot EE = k 2 8 ( x , y ) E .

Рис. 1. Поперечное сечение прямоугольного волновода

Полагая, что зависимость поля от продольной координаты z и от времени имеет виде e - i p z + i ш t (т. е. eE ( x , y , _г ) = j E _± ( x , y ) e - i p z ) из (6) получаем три уравнения относительно x -, y - и

a E y

dy   n y=0

= 0,

d E y d y

y = H

z -составляющих электрического поля:

d ² E x d yy 5 2 E y d x ²

⁺ ( ^k 2 ^e( x , ^y ) ^- P 2 ) ^Ex

⁺ ( ^k 2 ⁸ ( x y ) —P ² ) ^Ey

d ² E z + d ² E z d x ²     d y ²

= 0,

-

-

d E d x d y d ² E x d x d y

+ i e^ E z = 0; d x

+ i p^ E z = 0; d y

d E„

+ k 2 8 ( x , y ) E z + i p' ^x + i p — y = 0. d x     d y

Зависимость компонент электрического поля E_x , E_y , E_z от поперечных координат будем искать в виде

и заменяя бесконечный предел суммирования на конечное число Ì , выражения (8) приводим к виду:

MM

E x = EX A p , _r cos ( n p x ) sin ( 9 _ry ) ;

p =0 r =0

MM

E y = XX b p , r sin ( ⁵ p x ) cos ( X г У ) ;          (10)

p =0 r =0

MM

Ez = XX Cp ,r sin (кpx) sin (cry), p=0 r=0

где

ж ж

^Ex = XX ( A p sin ( ^a p x ) ⁺ A p cos ( n p^x ) ) ^x p =0 r =0

x ( a r sin ( 9 _ry ) + a_r cos ( 9 _ry ) ) ;

n p	_ n p = H ’	9 r	n ( r + 1 )	5 p	n ( p + 1 )
			H ’		W
x r	n r	к p	n ( p + 1 )	, c r	n ( r + 1 )
	H ’		W		H

ж ж

^Ey = XX ( B p ^sin ( ⁵ p^x ) ⁺ B p cos ( ⁵ p^x ) ) ^x p =0 r =0

X ( b r sin ( x г У ) + b r cos ( x г У ) ) ;

p = 0,1,... M , r = 0,1,... M .

×лены сумм (10) образуют ортогональный базис, соответствующий граничным условиям (9).

Запишем выражения (10) в следующем виде:

ж ж

E z — ZZ ( C p sin ( к p x ) + C p cos ( к p x ) ) x p =0 r =0

Ex

x ( c_r sin ( c _ry ) + 5_r cos ( c _ry ) ) .

Подчиняя компоненты (8) граничным условиям:

E     = 0,  E= zx=0

E     = 0,  E= zy=0

E     = 0,  E= x y=0        xy=h

E y

E z

d Ex	= 0 ,	d Ex	= 0,	(9)
d x	y =0	d x	y = W

E = 0, E = 0, yx =0        yx = W

N

X a n ^cos ( n =0

N

X b m ^sin

( a⁽ _n ^x ) x ) sin ( y ^x ) y ) ,

( « m ) ^x ) ^cos ( ? m ) y ) ,

m =0

N         ( z )         ( z )

X C t sin ( a t ^ x ) sin ( y t ^ y ) , t =0

где N = ( M + 1)² - 1. При одиночном суммирова-

нии (11) учитывается весь спектр функций (10).

Коэффициенты а П , ^y , z ) и y^{( x} , ^y , z )

в следующем виде:

и у.

n

записываются

( x )          =        ( x )

^a p + ( M +1 ) r   ^{П p} , ^Y p + ( M +1 ) r

= ⁹ r ^;

( У )         _ x ( У )         _

“ p + ( M +1 ) r = ° p ’ ^Y p + ( M +1 ) r = ^X r ’

_a ⁽ z )

p + ( M +1 ) r

_       ( z )

= ^K p ’ ^Y p + ( M +1 ) r

^G r ,

где p = 0,1,... M , r = 0,1,... M . Например, при M = 2 они запишутся в виде

“ ( x ) = ( п о , П 1 , П 2 , П о , П 1 , П 2 , П о , П 1 , П 2 ) T ;

У⁽ x ) = ( ^ 0 , $ 1 , $ 2 , ^ 0 , $ 1 , $ 2 , ^ 0 , $ 1 , ^ 2 ) .

Таким образом, решение задачи о расчете волноводов с произвольным заполнением сводится к представлению электрического поля в виде (11). Связь между x-, y-, z-составляющими поля в (11) определяется коэффициентами an , bm, ct, значения которых находятся из системы алгебраических уравнений, получаемой в результате подстановки (11) в (7) и использования условий ортогональности базисных функций разложений (10), (11). Подставив выражения (11) в систему (7), получим:

N    Г/    чх2     „1

-У an (y^n ^) +Р2 cos (“Vx) sin (yVx) + n=0    ^              J

N

⁺ k У a n ^e ( ^x , У ) cos ( “ Lx ) ^x ) sin (y^ ) У ) n =0

N

+У bm “m )Ym) cos ( “(y) x] sin Uy)) y) + mm m   mm m =0

N    (z)        (z)(

+ i в У C t a t cos ( a t x ) sin ( Y t У ) = 0;

t =0

N

-

N/ 442

У b m ( “ m ) +P ^{2 sin}

( “ m ) x ) cos ( Y m ) У ) +

m=0    ^

N

+ k o у b m ^e ( x , у ) sin ( “⁽ m ) x ) cos ( Y⁽ m ) у ) m =0

N

+ У a n “ n ) Y⁽ n^x ) sin ( “ nx ) x ) cos ( Y nx ) У ) + n =0

^N ( z )       ( z )          ( z )

+ i в У C t Y t sin ( “ t x ) cos ( y i У ) = 0;

N

-

■ У c t ( “^{( z} ) ) + ( y^{( z} ) )    ^sin ( ^{a ( z} ) x ) ^sin ( v tz ) У )

+

+

-

-

N k2 У Cte (x, У) sin (“tz)x) sin (Ytz)У) -

N ip У an “n) sin (“nx)x)sin (Ynx)У) n=0

N ip у bmym^ sin (“ax) sin (yma)

m =0

-

= 0.

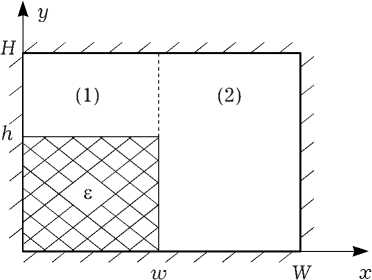
Рис. 2. Прямоугольный волновод с угловым координатным диэлектрическим заполнением

Проецируя систему уравнений (12) на соответствующий базис собственных функций, ум- ножаем:

1-е уравнение системы (12) – на cos (“^x) x) sin (Yqx) У), q = 0... N;

2-е уравнение системы (12) – на sin (“^y) x) cos (Yqy) y), q = 0... N;

3-е уравнение системы (12) – на sin (“^z)x) sin (Yqz)y), q = 0...N и интегрируем все три уравнения системы (12) по сечению (j0H /O^dxdy).

В результате получаем систему матричных уравнений относительно коэффициентов разложений (11). Приравнивая нулю определитель ма- трицы, получаем дисперсионное уравнение волн прямоугольного экранированного волновода с произвольным диэлектрическим заполнением. Отметим его особенности.

В составляемом таким образом матричном уравнении лишь три матрицы зависят от функции диэлектрического заполнения e (x, y) , которые при этом не зависят ни от частоты, ни от значения продольного волнового числа. В результате все матрицы, входящие в дисперсионное уравнение, при любом сколь угодно сложном характере диэлектрического заполнения считаются один раз. Ýто позволяет существенно сократить время расчета дисперсионных характеристик.

Для проверки действенности предложенного подхода рассмотрим тестовую задачу, ранее решенную [2] на основе метода частичных областей. Проведем с помощью предложенного метода расчет направляющей структуры, представленной на рис. 2.

Параметры структуры: W = 8 мм, w = 5 мм, H = 10 мм, h = 6 мм, e = 6. Расчет данного вол-

₽'

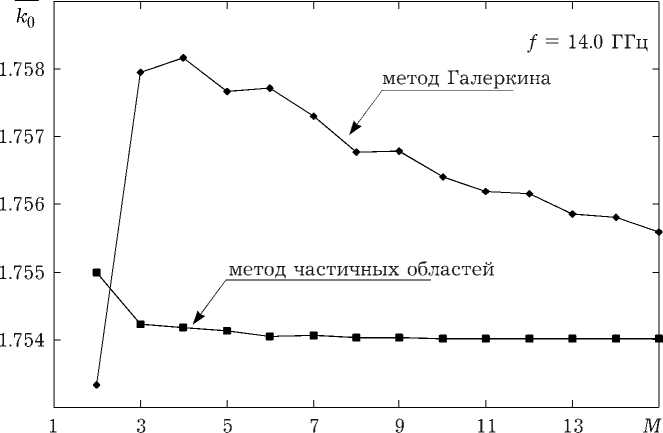
Рис. 3. Сходимость модифицированного метода Галеркина и метода частичных областей

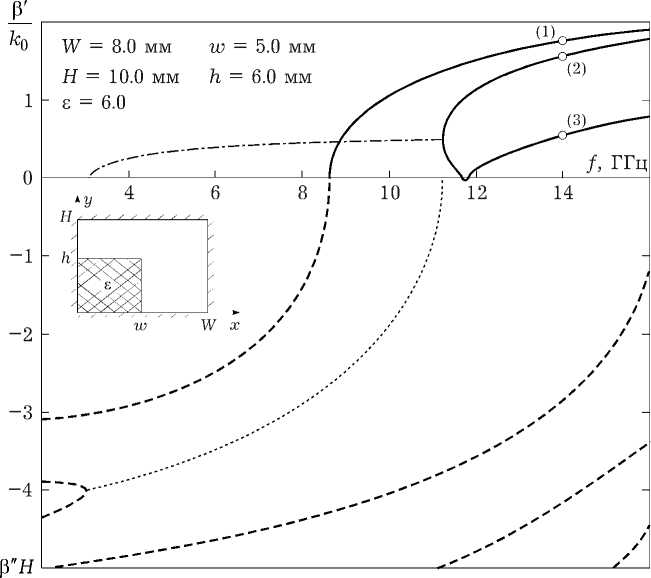
Рис. 4. Дисперсионные характеристики прямоугольного волновода с частичным диэлектрическим заполнением

новода проводился двумя методами: предложенным модифицированным методом Галеркина (ММГ) и методом частичных областей, при котором анализируемая структура разбивалась на области (1) и (2) (рис. 2), поля в которых представлялись с использованием аппарата LM и LE -волн. Детальное изложение данной методики расчета приведено в [2].

Решения дисперсионного уравнения, полученные при различных порядках приближения двумя способами, приведены в таблице ниже и на рис. 3.

Видно, что результаты, получаемые обоими методами, сходятся к одному и тому же значению, при этом результаты близки уже в малых приближениях (при M = 5 нормированные постоянные распространения, полученные разными методами, отличаются лишь на 0.2 %).

С помощью М×О и ММГ были рассчитаны дисперсионные характеристики волн данного волновода в частотном диапазоне от 2 ГГц до 16 ГГц (рис. 4). Результаты расчетов практически полностью совпали (дисперсионные кривые графически неразличимы). Как видно из рисун- ка, в спектре собственных волн волновода присутствуют комплексные волны (КВ) [3–5], дисперсионные характеристики которых начинают в точках жордановой кратности волновых чисел [6].

Предлагаемый метод расчета волноводов, неоднородно заполненных диэлектриком, является универсальным: единственное ограничение – внешняя металлизированная граница должна быть координатной. При этом легко формируется базис представления полей. Метод обладает преимуществом по сравнению с М×О при решении задач подобного класса, так как не требует введения в частичных областях, для которых нельзя сформулировать краевую задачу Штурма – Лиувилля, непрерывного спектра собственных функций [7].

Метод прост в алгебраизации дисперсионных задач и среди множества компьютерных методов представляется наиболее строгим и математически обоснованным.

Описанная методика демонстрирует возможности прямых вариационных методов при отказе в них от наложения на поля условия калибровки Лоренца.

Таблица