О критерии выбора походок шагающей машины

Для безопасного передвижения транспортно-технологических шагающих машин необходимо обеспечить их постоянную статическую устойчивость при движении. При заданном коэффициенте режима работы движителей это свойство определяется выбором походки машины.

Корпус машины, движущейся по поверхности с препятствиями в пределах величины адаптации ног, перемещается в плоскости, параллельной горизонталям. Движения ноги характеризуются траекторией ее опорной точки, за которую принята точка центра стопы ноги. У ортогональных шагающих движителей проекции траекторий опорных точек на горизонтальную плоскость корпуса не зависят от длины выдвижения ног. Поэтому для рассматриваемого случая движения можно провести планаризацию, для этого достаточно спроектировать опорные точки опертых ног на горизонтальную плоскость, проведенную через центр тяжести корпуса. Считая, что ноги невесомые, масса машины сосредоточена в геометрическом центре корпуса, получим плоскую модель. Такая планарная модель машины дает возможность свести задачу статического равновесия к геометрическому исследованию, при котором определяется положение центра тяжести корпуса по отношению к опорному многоугольнику, образуемому опорными точками опертых ног. Количественно устойчивость оценивается величиной запаса устойчивости, под которой понимается измеренное вдоль продольной оси машины расстояние от проекции центра тяжести до границ опорного многоугольника. Конфигурация опорных многоугольников неоднократно меняется в течение каждого цикла походки, так как в процессе ходьбы разные ноги то становятся на землю и включаются в опорный многоугольник, то отрываются от земли и должны исключаться из рассмотрения. За критерий выбора походки здесь принята величина минимального запаса устойчивости за цикл походки [1].

Для рассматриваемого случая движения построены области существования статически устойчивых походок шестиногих и восьминогих машин [2, 3].

На поверхностях со значительным уклоном или с препятствиями, превышающими величину адаптации ног, появляется необходимость движения с определенными углами крена или тангажа корпуса. При этом точка приложения вектора силы тяжести в опорном многоугольнике смещается относительно положения геометрического центра корпуса, в опорных точках возникают дополнительные сдвигающие силы. Такой случай может также возникать при использовании машины в качестве тягача.

Для оценки условий устойчивости машины в этих условиях необходимо изменить расчетную модель шагающей машины, которую представим следующим образом. Плоская рама корпуса и ноги в виде невесомых стержней, выдвинутых на одинаковую длину, представляют собой цельную, абсолютно жесткую конструкцию в соответствии с рисунком 1. Ноги соединены в своих опорных точках с опорной поверхностью упругими связями. Эти связи обладают постоянной и одинаковой для всех ног упругой податливостью как в нормальном по отношению к опорной поверхности направления, так и в касательном направлении. Таким образом, они одинаково воспринимают как силы сжатия-растяжения, так и сдвигающие силы.

При отсутствии всех внешних сил опорные точки стоящих ног расположены на одинаковых расстояниях от точек прикрепления упругих связей к опорной поверхности таким образом, что точки прикрепления являются проекциями опорных точек на эту поверхность. При приложении к корпусу внешней силы в опорных точках возникают реакции, пропорционально которым и перемещаются опорные точки вместе с системой корпус-ноги. Перемещения опорных точек, как и распределение реакций между ними, будут различными в зависимости от взаимного расположения этих точек.

Положение каждой опорной точки определяется позицией ноги. Если же все опорные точки стоящих ног соединить отрезками прямых, получим опорный многоугольник, который точнее назвать в этом случае многоугольником нагрузки. Так как система корпус-ноги принята абсолютно жесткой, то и многоугольник нагрузки будет неизменяемой , абсолютно жесткой конструкцией, через которую на связи действуют силы и моменты, приложенные к корпусу.

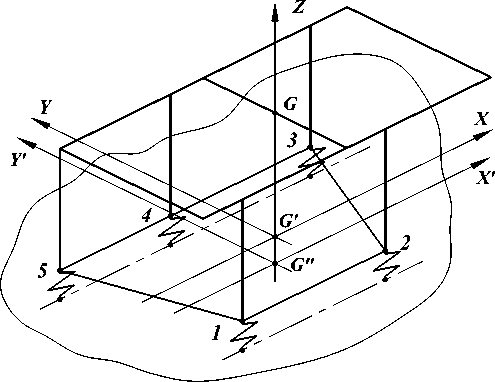
Рис. 1. Расчетная модель шагающей машины: 1, 2 ... 5 - опорные точки стоящих на поверхности ног, многоугольник 12345 - опорный многоугольник, или многоугольник нагрузки

При отсутствии всех внешних сил проекцию геометрического центра корпуса G на многоугольник нагрузки обозначим через G' , а проекцию этой же точки на опорную поверхность - через G" . Построим системы координат GXYZ и G'X'Y'Z' с началами в точках G' и G" , и с координатными осями G'X и G"X' , параллельными продольной оси корпуса и направленными в сторону движения шагающей машины.

Сила, приложенная к корпусу, будет поворачивать многоугольник нагрузки вместе с системой корпус-ноги вокруг оси, проходящей через точку, которую назовем центром опоры данного многоугольника нагрузки. Вследствие одинаковой жесткости связей во всех опорных точках положение центра опоры A в системе координат G'XY в соответствии с рисунком 2 определяется соотношениями:

Х

n

Z Xi

_ i = 1      .

;

n

Y A

n

Z Y

i = 1

n

где n - число опертых ног;

X i , Y i - координаты опорной точки i-й ноги в системе G'XY .

Центр опоры A (см. рис. 2) примем за начало осей координат Axyz, причем оси Ax, Ay, и Az параллельны осям G'X, G'Y и G'Z. Сила, проходящая через центр опоры, распределяется между опорными точками равномерно. Тогда, разложив силу, проходящую через точку A , на составляющие Fx, F у и Fz, имеем:

F cai= ' -----; F oai = F z /n.                                 (1)

n

Здесь F cai и F oai – соответственно сила, сдвигающая и отрывающая i -ю опорную точку.

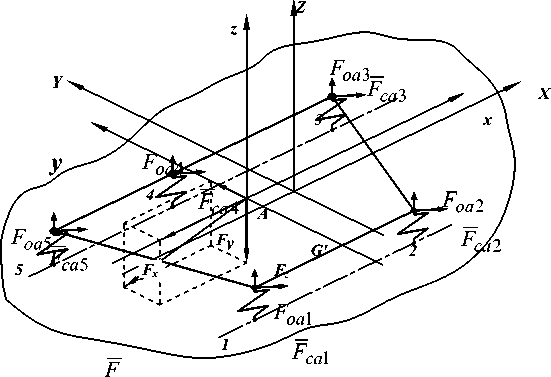
Рис. 2. Многоугольник нагрузки и силы, возникающие в опорных точках от внешней силы F: A – центр опоры многоугольника; F ca 1 F ca 5 и F oa 1 F_{oa 5} – сдвигающие и отрывающие силы, возникающие в опорных точках

Рассмотрим теперь, какое влияние на величины сил, действующие на опорные точки ног, оказывают приложенные к корпусу моменты Mx , My и Mz в соответствии с рисунком 3. Каждый из этих моментов вызывает смещение опорных точек относительно осей координат

G"X'Y' Z' в плоскости действия момента. Величина смещения X i каждой из этих точек зависит от ее положения. Для всех случаев нагружения корпуса внешними силами примем, что смещение центра опоры A достаточно мало для того, чтобы не оказывать влияния на величину моментов, возникающих от этих сил.

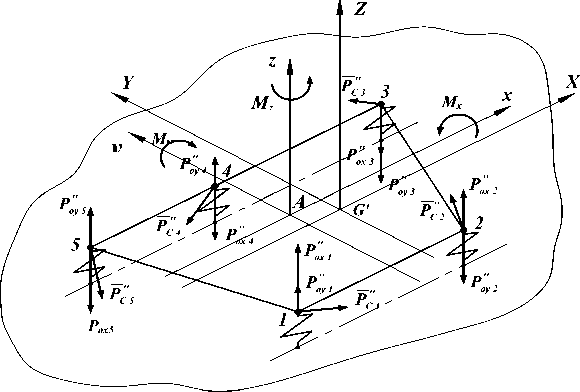
Рис. 3. Многоугольник нагрузки и силы, возникающие в опорных точках от внешних моментов

M x , M y и M_z : F_{cz 1}   F_{cz 5} – сдвигающие силы, возникающие в опорных точках от действия M _z ;

F_{ox 1}    F_{ox 5} и F_{oy 1}    F_{oy 5} – силы отрыва–прижима от действия соответственно M x , M y

От действия момента M_z в опорных точках появляются сдвигающие силы F_{cz i} . Условие равновесия имеет в этом случае вид

n

Мz = F cz1 ‘ ^l1 + F cz 2 ‘ ^l 2 + ... + F czn ‘ l n = X F czi ‘ l i , i = 1

где l i = xx ^ + y i - расстояние от i-й опорной точки до центра опоры A.

Сила F czi вызывает пропорциональное перемещение X i опорной точки, а так как жесткость упругих связей всех опорных точек одинакова, то:

A AA

—— = —— = ... = —— = const.

F cz 1    F cz 2

Вследствие абсолютной жесткости системы корпус–ноги должно соблюдаться следующее условие:

'2 = А2 = = An = const.

• l1     l2

Последовательно разделив члены равенств (4) на члены равенств (3), получим

Fcz1 = Fz^ = ... = Fczn = cOnst.

• l1         l2

Умножая каждый член ряда (5) на соответственно равное единице отношение и используя свойство ряда равных отношений, получим:

Fcz 1 = Fcz2 = = Fczn = Fcz1 " l1 = Fcz2 ' l2 = = Fczn ' ln = l1        l2      ...     ln          l12             l22         ...l

n

^{X F}czj • l j j = 1

n

X l j ²

j = 1

F czi ■ ^l 1 ⁺ F cz 2 • ^l 2 ⁺ ... ⁺ F czn " ln l i + l 2 + ... + l n

Отсюда, с учетом (2), имеем соотношение для i -опорной точки:

F czi l i

M z ; n

X lj j=1

к - Mz ■ li ^Fcz i n

X lj j = 1

.

Величина q = X^l 'jj- является геометрической характеристикой взаиморасположения ног в j = ¹

многоугольнике нагрузки, которую по аналогии с геометрической характеристикой сечения в науке о сопротивлении материалов назовем полярным весом многоугольника нагрузки.

От действия моментов M x и M y в опорных точках появляются силы прижатия–отрыва

F oxi и F oyi . Произведя выкладки, аналогичные проведенным выше, но только относительно осей Ax и Ay , получим выражения:

^мх • У/           M У • ^xi

xiyi

F oxi n         ; F oyin

X У j2

j =1

Геометрические характеристики

n

Q x = X y 2 ;

j = 1

n

Qy = X xj j=1

назовем осевыми весами многоугольника нагрузки.

Осевые веса принимают максимальные значения при осях координат Avu , повернутых относительно осей координат Axy на угол 0. Для нахождения этого угла выразим осевой вес многоугольника нагрузки Qu через координаты x j и y j

Q u = Z (y j • cos 6 - x j • sin 6 ) ² •

Дифференцируя выражение (8) по углу 9 и приравняв полученное выражение нулю, получим значение угла:

1          2 • Q xy

6 = -rafgtg -------—,

2      Q y — Q x

n где Qxy = Z Xj • yj — центробежный вес многоугольника нагрузки.

j = 1

Максимальное значение осевого веса будет относительно оси Au

Q_x + Q_v Г Qx — Qx ) ²

= w—- . ₊ I v y I ₊ q

Q max 2 I 2 I xy а относительно оси Av значение осевого веса минимально

Q min

Q x + Q y  Г Q

—

---Qy I + Qxy 2 i xy

Тогда силы прижатия–отрыва

M v и M_u в соответствии с (7):

F ovi и F oui

в опорных точках от действия моментов

F

. Mv • ^Ui . ovi                          ;

^Q min

M • v,-

F ui oui =              ,

^Q max

где v i и u i - координаты опорных точек в системе координат Avu , повернутой на угол 6 относительно системы Axy ;

M_v и M_u - моменты внешних сил относительно осей системы Avu после приведения их к центру опоры многоугольника нагрузки.

Внешние силы, приложенные к корпусу машины, - это, например, сила тяжести машины, направление вектора которой относительно корпуса определяется углами крена и тангажа при движении; сила тяги, если машина используется в качестве тягача; реакция от рабочих органов технологического оборудования. Эти силы, действующие на корпус машины, можно привести к центру опоры многоугольника нагрузки в виде силы и момента, после чего силы, действующие на опорные точки, могут быть определены в соответствии с выражениями (1), (6), (9). Суммарные значения силы прижатия-отрыва Foi и сдвигающей силы Fci, действующие на i-ю опорную точку многоугольника нагрузки или опорного многоугольника, равны:

F = F + F + F ■ oi oai ovi oui rr r

F = F , + F, . ci cai czi

Условие статической устойчивости шагающей машины при определенном опорном многоугольнике походки :

Fпр i = (Foi — Fci 1 f) > 0 , где Fпр i - приведенная сила для i-й опорной точки;

f - коэффициент сцепления стопы с грунтом;

i = 1,..., n , n - число ног в данном опорном многоугольнике.

Определяя F_n pji = ( F_o ji — F cji I f ) >  0 для каждого j-го многоугольника ( j = 1,..., m ) из m опорных многоугольников, образующих конкретную походку, в качестве критерия оценки походки выберем минимальное значение приведенной силы F пр min :

F пр min mln F пр ji .

Тогда при заданных условиях эксплуатации и таких характеристиках машины, как максимально допустимые значения тангажа и крена при движении, можно произвести сравнительную оценку возможных походок, выбор оптимальной походки для определенных условий движения или работы оборудования шагающей машины.

Данный критерий оценки походок был апробирован и экспериментально проверен при выборе походок шестиногого макета шагающей машины с постоянной длиной выдвижения ног, перемещавшегося по стальному листу. Углы тангажа и крена корпуса машины создавались соответствующими наклонами стального листа.