О квантовом описании движения микрочастицы в среде с вязким сопротивлением

Квантовое описание движения консервативных систем хорошо разработано и практически не встречает в научной среде дискуссий принципиального характера. Квантовая механика. таких систем приводит к одинаковым результатам в различных представлениях. Динамика, в этих случаях определяется унитарными операторами эволюции.

Реальные же физические системы в подавляющем большинстве являются открытыми. В таких системах приходится учитывать необратимые процессы релаксации, происходящие в соответствии со вторым началом термодинамики.

К настоящему времени предложены различные подходы к квантово-механическому описанию движения в открытых средах. Отметим, например, работы [1-10]. Наиболее простым и продуктивным нам представляется подход, предложенный в [1-5], где используется канонический формализм с явно зависящим от времени гамильтонианом.

Настоящая работа посвящена применению данного подхода к описанию и анализу движения квантовой микрочастицы, подверженной силе вязкого сопротивления в отсутствие действия других консервативных сил.

2.    Каноническое квантование

Уравнение движения классической точечной частицы, положение в пространстве которой в момент времени t характеризуется радиус-вектором r(t), в вязкой среде имеет хорошо известный вид

Г + y r + VU/m = 0,                             (1)

где т - масса микрочастицы, у - коэффициент сопротивления движению частицы со стороны вязкой среды, U = U ( г ) - потенциальная энергия, создаваемая действующей на частицу внешней консервативной силой, точка над r обозначает производную по времени.

Заметим, что данное уравнение можно переписать следующим образом:

(m Г e^7t) = - V (Ue^7t).                                  (2)

Введя канонический импульс

Р е = т Г е⁷ ,                                      (3)

перепишем (2) в виде уравнения Гамильтона:

Р е = -VH, где гамильтониан Н = f (pе,t) + U(r)e7t, f (ре, t) - подлежащая определению функция. Для нахождения f (pе,t) запишем другое уравнение Гамильтона:

. ЭН r = ЭрС.

Отсюда и из (3) имеем

.    Ре r = —е т

-

7t = df Э р е .

Следовательно, f(p_е,t) = р 2е ^7t /2т. Таким образом, классический гамильтониан, соответствующий уравнению (1), имеет вид

Н = ^Р2- е 2т

-

^7t + U ( r )e^7t.

Заметим, что функция Н в данном случае не является энергией осциллятора, так как явно зависит от времени.

Следуя процедуре канонического квантования, заменим канонически сопряженные переменные r и р _с их эрмитовыми операторами Г и р _с. Далее наложим на их декартовы компоненты ж = х1, у = х₂, г = жз и р_еж = р_е1, р_еу = р_е2, p_ez = р_ез стандартные коммутационные соотношения

[ту ,Рек ]     i~^jk,

где ~- постояшіая Планка. 5jk - символ Iхроыекера. j,k = 1, 2, 3.

Переходя к координатному представлению, согласно которому r = r, рс = -~V, при учете (4) уравнение Шредингера для волновой функции ф запишем в виде г~^г = -т^е 7tV2^ + U(r)e7tr.                         (6)

Легко видеть, что из (6) следует уравнение непрерывности

ITt +(^v • ^j) = ⁰’                                     ⁽⁷⁾

где р = |ф|2, а ток вероятности j = Д-  '(^*W — ^W*).

2тг

Интегрируя (7) по пространственному объему V с учетом то го, что ток j на его границах обращается в нуль, получим ^J|^|²dV = 0. Отсюда находим J|r|²dV = const. Таким образом, как и в консервативном случае, квадрат нормы волновой функции является постоянной величиной. Следовательно, в присутствии вязкого трения величина |ф|², как и в случае консервативных сил, имеет смысл плотности вероятности нахождения квантовой частицы в точке с определенной координатой. Тогда справедливо условие нормировки [ |ф|² dV = 1.

3.    «Свободное» движение в вязкой среде

Рассмотрим «свободное» движение квантовой частицы в среде с вязким трением, когда отсутствуют все другие, в том числе консервативные силы. Для этого положим в (6) U = 0.

Для решения уравнения (6) представим ^( r ,t) в виде преобразования Фурье:

+^ r(r,t) = j 9k(t)е^гk•^rd³ k .

-∞

Подставляя (9) в (6) при U = 0, получим 9 к = —г ~к² е ^7t p k /(2m) После интегрирования будем иметь 9k(t) = 9к(0)exp[—г~ к ²(1 — e^-7t)/(2my)]. Тогда (9) примет вид

Г              ~ к ²

9k^(0)exp^[— г- ---⁽¹

2ту

-∞

— e^-7t) + г k • r ]d³ к .

(Ю)

+^

При t = 0 из (9) находим Ф ( г , 0) = J 9_k(0)е^гk•^гd ³k. Отсюда

-∞

9к(0) =

(= У

+^

[ Ф ( г , 0)е^-ik•^rd³ r .

(И)

-∞

Соотношениями (10), (11) определяется общее решение задачи о «свободном» движении квантовой частицы в среде с вязким сопротивлением.

Пусть волновая функция в начальный момент времени имеет вид

Ф ( г , 0) =

1 У374ур

. г2

exP(—;Д2 + г^0г), 2Z0

где г2 = ж2 + у2 + г2, Zq - характерный начальный пространственный радиус локализации плотности вероятности, mvo к0 = -^, ~

«о - начальная скорость микрочастицы, направленная вдоль оси г.

Тогда из (10) - (12) получим следующее решение уравнения (6) при U = 0:

	,z                  1                Г г2 - гкоГ2(2г - «от) 1 *(r’ )    ,3/4Го3/2(1+ іт ) 3 / 2 CxP[       2Го(1+ іт )     ]•	(14)
Здесь

Т = -~2 ^т, ТП-І0

1 - е-⁷ т =------

Из (11) следует выражение для плотности вероятности обнаружения микрочастицы в точке с координатами ж, у, г в произвольный момент времени t;

И^(г’< = ^312^3 ^exp

-

г² + (г - «от)² Г²

7         7 ,    7

где г 2 = ж² + у²,

Г = Го V 1 + Т2 .

Таким образом, имеем локализованный домен плотности вероятности, максимум которого движется вдоль оси г по закону г = — (1 - е-74). 7

При этом, как видно из (18), (15) и (16), радиус Г пространственной локализации с течением времени увеличивается согласно выражению

Г = Го V1 + Т2 = Го V1+ 2(1 - е-74)2,                        (20)

где

~

Т^ =    /2.

П7 Го

Заметим, что по закону (19) движется классическая частица, которой в вязкой среде сообщена начальная скорость «о.

При t >>  1/7 после прохождения вдоль оси г дистанции г^ = «о/7 происходит практическая остановка домена с «заморозкой» радиуса его пространственной локализации на значении Г^ = Го Д1 + т^ ■

Похожая ситуация встречается при формировании в неравновесных средах стационарных диссипативных солитонов [П, 12]. Однако, в отличие от случая диссипативных солитонов, радиус Г^ сформировавшегося статического домена плотности вероятности зависит от радиуса Го домена на входе в среду. Заметим, что совсем недавно были предсказаны солитоноподобные объекты в диссипативных средах, также сохраняющие память о входных условиях [13]. Таким образом, аналогия между рассматриваемым здесь статическим доменом плотности вероятности и стационарными солитоноподобными объектами в диссипативных средах становится ближе.

Если 7 = 0 (консервативный случай), Г^ ^ то. То есть свободная частица по истечении достаточно длительного промежутка времени может быть обнаружена в любой точке пространства. Вязкое же трение препятствует полному расплыванию волнового пакета плотности вероятности, ограничивая его присутствие в определенной области. Таким образом, движение «свободной» квантовой частицы в среде с вязким трением является финитным в отличие от инфинитного движения свободной частицы в консервативной среде. В то же время, несмотря на финитный характер движения, как это можно легко увидеть, энергия и импульс микрочастицы в вязкой среде не квантуются, а принимают непрерывный ряд значений.                                                    _________

Исследуем динамику неопределенностей координаты Аг = (г2) — (г)2 и соответствующей декартовой компоненты импульса Ар^ =  (р^ — (pz)2 микрочастицы при описанном выше движении [14]. Здесь скобки (...) обозначают квантовое среднее. Учитывая (3) и (5), запишем в координатном представлении оператор физического (не канонического) импульса: p = —z~e-7tV. Используя также (14), будем иметь

АРг =

V2Zo ^.

Аналогично для неопределенности координаты получим

Аг ='«^ ■

Точно так же выглядят выражения для неопределенностей двух других декартовых компонент импульса и координаты.

Из (22) и (23) находим

D(t) = Аг • Ар_г = D_c(t)e^-^, (24) где

Dc(t) = Аг • Ар, = ~ _х т. (25)

Полагая в (24) и (25) t = 0, пол учим D(0) = D_c(0) = ~/2. Это значение функции неопределенностей «координата - время» соответствует когерентному начальному состоянию микрочастицы, минимизирующему соотношение неопределенностей [15].

При t >  0 каноническая функция неопределенностей D_c(t) испытывает монотонный рост, удовлетворяя в соответствии с фундаментальными принципами квантовой теории неравенству D_c(t) > ~/2.

Характер зависимости D(t) определяется значением параметра т_Д (см. (21)). Если Т_Д< 2 V2 ~ 2, 83, функция неопределенностей монотонно уменьшается с течением времени. В противоположном случае в зависимости D(t) имеются два экстремума. Внутри временного интервала 0 < t < ti функция D(t) уменьшается, достигая локального минимума при t = ti. Далее рост рассматриваемой функции до момента времени t2 сменяется монотонным спадом к нулевому значению при t ^ то (рис. 1). Здесь времена ti,2 определяются выражениями

1^ =

Щ+Д(3 т \F

„ 2 ) .

тД

Столь нетривиальная зависимость функции неопределенностей от времени обусловлена, в частности, тем, что, согласно (22) и (23), неопределенность физического импульса падает с течением времени, а неопределенность координаты возрастает.

С увеличением параметра тД ^ВР^емя t1 ~ 2/(7тД) значительно уменьшается, а соответствующий этому времени минимум функции неопределенностей становится едва заметным. В этих же условиях время t2 достигает значения t2 = ln2/y ~ 0, 693/у, а максимум функции D(t) становится более выраженным. По-видимому, можно сказать, что в этот момент времени квантовые свойства движения микрочастицы проявляются наиболее ярко. Монотонное уменьшение D(t) при t > t2 можно интерпретировать как подавление вязким сопротивлением квантовых свойств движения микрочастицы.

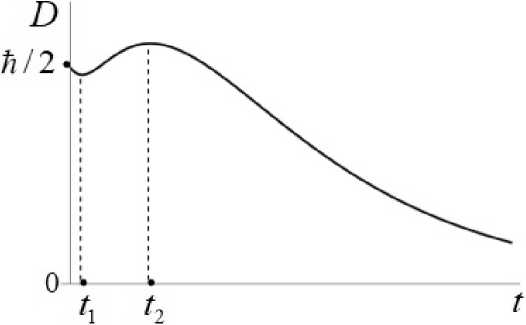
Рис. 1. Зависимость функции неопределенностей «координата - импульс» от времени при ц^ = 4

Убывание функции неопределенностей «координата - импульс» до практически нулевого значения не противоречит фундаментальным принципам квантовой теории. Здесь важно, чтобы значения канонической функции неопределенностей D_c(t) всегда превышали ~/2. Данное правило следует из (25) и гарантировано коммутационными соотношениями (5).

Вязкое сопротивление обусловлено взаимодействием рассматриваемой микрочастицы с большим коллективом частиц среды. Это способствует локализации волновой функции микрочастицы и, следовательно, возможности ее регистрации. Данное обстоятельство используется, например, в камере Вильсона и в пузырьковой камере [16], выполняющих роль классических приборов по регистрации микрочастиц и измерению их параметров. Рассмотренная здесь теоретическая модель может быть использована при описании работы аналогичных приборов по регистрации нерелятивистских микрочастиц. Из (19) следует, что длина трека микрочастицы в средах данных камер определяется выражением ,с^ = го/у. При этом ширина трека у его окончания находится из (18) при ширине на входе, равной Iq. Эмпирический параметр у можно определить экспериментально, запуская на вход в камеру микрочастицы с заданными массами или скоростями и пользуясь формулами (18) и (19).

4.    Заключение

Исследование, проведенное в настоящей работе, показывает, что формализм канонического квантования достаточно адекватно и в целом успешно описывает движение микрочастицы в среде с вязким сопротивлением. С другой стороны, канонический подход обладает свойством неоднозначности. То есть, можно предложить отличные от (4) классические гамильтонианы, приводящие к уравнению (1). Это, в свою очередь, приведет к уравнению Шредингера, отличающемуся от (6). Здесь при выборе гамильтониана мы руководствуемся критерием простоты, считая, что гамильтониан (4) является наиболее простым из всех остальных, приводящих к уравнению (1). Такой подход привел нас к физически разумным результатам, способным найти приложения при описании движения квантовых микрочастиц в пузырьковых камерах. Следующим шагом на пути таких приложений может стать квантовое описание движения микрочастиц в пузырьковых камерах при наличии внешнего магнитного поля, сортирующего характеры искривления треков в зависимости от масс и зарядов частиц. Здесь задача может свестись к квантовому рассмотрению движения зату- хающего гармонического осциллятора, исследованного, например, в [1-4]. Некоторые уточнения этой модели и ее обобщение на трехмерный случай могут пролить дополнительный свет на характер квантового движения микрочастиц в регистрационных приборах типа пузырьковых камер. Следующим шагом может стать обобщение предложенной модели на релятивистские случаи для частиц с целым и полуцелым спином. Это позволит описывать регистрацию пузырьковыми камерами релятивистских квантовых частиц, включая космические лучи.