О месте нестандартных моделей

Можно изобразить эту конструкцию иначе и рассмотреть мир:

Vg:={(g,a) : aGV}=yM.

Если р — высказывание о множествах, то в нашей модели очевиден закон «переноса»: р((1,Л)) Е> р(Л) (т. е. (l,a) С(1,Ь)оаСби т. п.).

Несколько обобщим приведенную конструкцию. Пусть

V_{Q :}= yQ .₌ ^.Q^ у, domp = Q; imp С V}.

Пусть Л = Л( •) — некоторый элемент из Vq и р — формула теории множеств. Закон покоординатного моделирования не вызывает затруднений:

С этим правилом Vq очевидно становится моделью теории множеств. Однако из общих соображений кажется, что такая «послойная» модель никаких новых знаний нам не добавляет (хотя она и нестандартна).

Взглянем все же на Vq повнимательнее. Для этого положим

[р(Л)]:={де9:р(Л(д))}.

Возникает «оценка истинности» формул р как функция [ • ] со значениями в P^QY Понятно, что справедлив «принцип переноса»:

(р — теорема) -щ [р] = Q.

Нетрудно видеть, что справедливы соотношения:

k а VI = М ⁿ М. k v V] = М и [VL [0/^1 = Д>Ю1, № Л Д = 7,1^1

При этом верен и «принцип максимума»:

(Зж) р(ж) -д (Зж) [р(ж)] = Q.

Взглянем на объект 7^ := R^. Очевидно

^R, — поле вещественных чисел]] = Q,

• т. е. К моделирует поле вещественных чисел «внутри Vq».

Можно сказатв и иначе

КД := Д G V_Q : [г G ^J = Q} = >^Q,

• т. е. «спуск» поля вещественных чисел внутри Vq — пространство вещественных функций на Q.

Приведенную конструкцию можно несколвко обобщить, заменив Q на стоуновский компакт некоторой полной булевой алгебры В, a ^(Q) — на алгебру открыто-замкнутых подмножеств Q. Точнее говоря, определяя новый «нестандартный» универсум множеств V^^B\ положим

VW _{: =} {_{ж :} Др _е а) х : dom(z) > В A dom(z) С V<^B)},

^ := J уД, абОп где а пробегает класс ординалов On.

Булева оценка истинности [<Д] определяется рекурсией по сложности <р при естественной интерпретации логических связок и кванторов. Оценки же атомных формул ж G у и х = у для х,у G У<^в) определяют схемой трансфинитной рекурсии:

k G у] := У у(г)А^ = ж]|: zGdom(y)

к = у]:= Д хД) => [г G у] А Д уД) => Д G ж].

2Gdom(a?)                    2Gdom(?/)

(Знак => символизирует импликацию в В.)

Так возникает булевозначный универсум V^^B\ моделирующий универсум фон Неймана V. При этом поле вещественных чисел К в новой модели имеет своим спуском расширенное ^-пространство КД база которого изоморфна исходной булевой алгебре В. Тем самым получает обоснование эвристический принцип Канторовича, и теория булевозначных моделей превращается в аппарат одного из классических разделов функционального анализа.

Теория булевозначных моделей, ставшая основой «булевозначного анализа», восходит к Д. Скотту, Р. Соловею, П. Попенке и Г. Такеути. Более известно направление моделирования, получившее название от своего основателя А. Робинсона «нестандартный анализ». В настоящее время все чаще используется более точный термин «инфинитезимальный анализ», подчеркивающий связь новой теории с классическими воззрениями дифференциального и интегрального исчисления, возникшего в форме «анализа бесконечно малых».

С технической точки зрения модели инфинитезимального анализа могут рассматриваться как простейшие разновидности булевозначных моделей. Однако значение инфинитезимальных методов столь велико, что робинсоновский анализ занимает совершенно особое место. Достаточно сказать, что именно в нем нашли объяснение методы, основанные на использовании актуальных бесконечно больших и бесконечно малых чисел (в частности, теория неделимых Кавальери и монадология Лейбница).

Развивая инфинитезимальный анализ, от обычного универсума фон Неймана V переходят к «оснащенному» универсуму V¹ так называемых внутренних множеств с отмеченными в нем реперными точками — стандартными множествами, составляющими

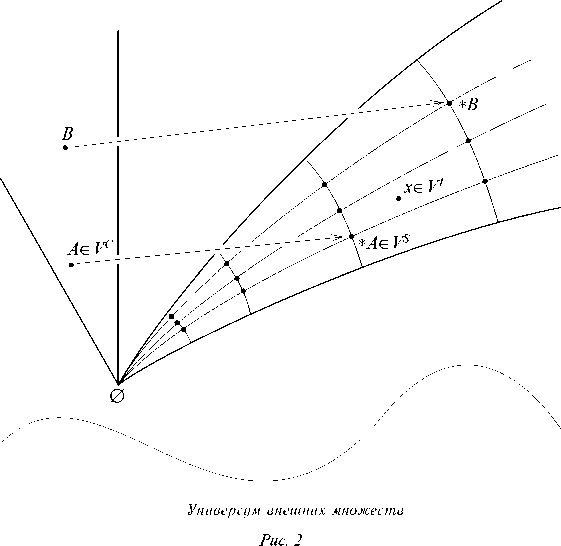
класс изображений — копии V^s обычного универсума V. Дальнейший анализ показывает что V¹ лежит в новом классе — в универсуме V^е внешних множеств, удовлетворяющих аксиоматике Цермело. В V^е выделен универсум «классических» множеств V^е — еще одна реализация мира стандартных множеств V^s. Точнее говоря, имеется *-изображение, поэлементно отождествляющее V^е и V^s. В силу аналогов принципов переноса V^е, V^s и V¹ можно рассматривать как «ипостаси» универсума фон Неймана V. Именно в этом сложном взаимодействии нестандартных моделей проходит весьма бурный современный этап возрождения, переосмысления и обогащения старинных инфинитезимальных методов.

Синтез технических приемов булевозначного и инфинитезимального анализа — это во многом все еще открытая проблема. С ее современным состоянием можно познакомиться по серии «Нестандартные методы анализа».