О методе экспонент в задачах моделирования нагрева металла в печах

В свое время М.А. Био предложил мгновенное распределение температуры в массивном теле по пространственным координатам представлять с помощью парабол [1]. Привлекательность такого подхода объясняется тем, что параболу можно однозначно характеризовать только одним параметром, что значимо упрощает описание температурного поля [2] и весьма существенно уменьшает необходимый для его хранения объем памяти компьютера. С этой же целью – с целью сокращения необходимого объема памяти компьютера – в работе [3] применялась аппрокси-

мация температурного поля слябов в методических печах многочленами второго и четвертого порядков по координате % - толщине нагреваемой заготовки. При этом начало координат выбиралось в точке с нулевым тепловым потоком, это позволяло исключить в аппроксимирующем многочлене наличие нечетных степеней координаты % и тем самым уменьшить количество подлежащих определению его коэффициентов.

Обоснованность такого подхода аргументируется также и тем, что, как указано в работе [4, с. 157], «…из решений уравнения теплопроводности … известно, что при постоянной

скорости нагрева и постоянном тепловом потоке с наступлением так называемого регулярного режима распределение температур по сечению пластины подчиняется параболическому закону».

Таким образом, метод парабол может показаться весьма привлекательным при решении задачи контроля температурных полей нагреваемых заготовок. Однако, как это отмечено в работе [2, с. 357], метод парабол «…не имеет решающих преимуществ перед методом гармоник или методом прямых», которые, кстати сказать, используются значительно чаще.

Постановка задачи

В работах [5, 6] для описания мгновенного распределения температуры по сечению нагреваемых заготовок предлагается использовать метод экспонент. Разумность и привлекательность такого подхода также объясняется как простотой описания, так и небольшим числом параметров, характеризующих используемую экспоненту. Вместе с тем данный метод в работах [5, 6] применяется без должного обоснования и аргументации, без указания того, насколько такое представление соответствует физическому описанию процесса нагрева. В работах [5, 6] этот метод используется для «…инженерного расчета» [5], оптимального по быстродействию управления нагревом, адекватность такого описания, как это нам представляется, оценивается только «…путем сравнения с известной методикой расчета с помощью номограмм» [5], изложенной, например, в работе [2]. Утверждается, что «…аппроксимация распределения температуры по толщине нагреваемого тела экспоненциальной функцией позволяет упростить расчет оптимального по быстродействию управляющего воздействия – температуры греющей среды и моментов переключения» [5, 6].

Метод экспонент может быть интересен в связи с тем, что для реализации режима реального времени в АСУ ТП нагревательных печей, несмотря на возросшую мощность современных компьютеров, по-прежнему привлекательны достаточно простые модели и алгоритмы. Поэтому существенно важным является вопрос о том, следует ли рекомендовать этот метод для использования в АСУ ТП, выяснить, насколько предлагаемое описание температурного поля все-таки соответствует общеизвестному математическому представлению процесса, насколько оно приемлемо, в том числе и для этих целей. Поэтому далее рассмотрим особенности применения этого метода.

Аналитическое решение задачи

Как это хорошо известно [7–11], нагрев слябов в методических печах можно представить с помощью математической модели следующей структуры:

дt(х,т) д     д^х,т)\ ср —— = rl^—),00;(1)

дт дх \ дх J

t(x, 0) = t0(x), 0 < x < L;(2)

-Ad^2 = a[tn(T)-t(0,T)],T>0;(3)

• д^=0,т>0.(4)

дх'

Здесь с,р и Л - соответственно теплоемкость единицы массы, плотность и коэффициент теплопроводности, зависящие в общем случае от температуры t(x, т); x - пространственная координата; т - время; L - расчетное сечение заготовки; t⁰(x) - заданная функция, описывающая начальное температурное поле металла; а - коэффициент теплоотдачи; t_п(т) - температура рабочего

пространства печи.

Согласно [5, 6] мгновенное температурное поле заготовки предлагается описать следующим соотношением:

t(x, т) = СПОв(т) • ехр[-ф(т) • x],(5)

где Спов(т) - температура поверхности; ^(т) - некоторая функция времени, подлежащая опреде- лению в процессе решения задачи.

Подчиним данное соотношение уравнению теплопроводности (1), для этого сначала вычислим его частные производные:

• дtXT2 = ^отИ • ехр[-^(т) • x] + СПов(т) • ехр[-^(т) • x] • (-x) • ^2;(6)

^дХг = £пов(т) • ехр[-^(т) • x] • [-^(т)];(7)

• д а?) = Спов(т) • expl-Нт) • x] • [-^(т)]2.(8)

  Если подставить полученные выражения в уравнение теплопроводности (1), то получим следующее соотношение:

  
  

  ⁽^¹ + С пов (т) ■ (-х) ■ ^ = а Т ■ С _ПО в (т) ■ [-^ (т)|²,

  
  
  
  

  где а Т - коэффициент температуропроводности.

  Данное дифференциальное уравнение включает две неизвестные функции времени С _пов (т) и ^(т) и, естественно, само по себе решено быть не может.

  Примечание. Конечно, с помощью граничного условия (3) С _пов (т) можно выразить через ^(т) и подставить в данное дифференциальное уравнение, однако в этом случае мы получаем достаточно сложное нелинейное дифференциальное уравнение относительно ^(т) , аналитическое решение которого не представляется возможным.

  Как нам представляется, в работах [5, 6] (без каких-либо оговорок) полагается, что при рассматриваемом режиме нагрева С _пов = const. В этом случае дифференциальное уравнение (9) заметно упрощается и будет иметь вид

  
  

  ⁽-хУ^^= а Т '[?(т)|².

  
  
  
  

  Данное уравнение является уравнением с разделяющимися переменными и сравнительно просто может быть проинтегрировано (х считается константой).

  
  

  -d^(i) _ а _Т , [Ф(т)|² = “ ’ ^т;

  /-^=/? •*+*

  ^=?^т+С;

  ^^(т) = г^ = 7777^.

  ——т+С   аг.т+с

  X

  
  
  
  
  
  
  
  
  
  

  Следует отметить, что именно соотношение (14) и предлагается для описания процесса нагрева в работах [5, 6].

  Как это следует из уравнения (14), ^(т) ^ 0 при 1^^. Здесь С - постоянная интегрирования, определяется она из начального условия

  
  

  _ф(0) = - ч С = 4г . С         ^(0)

  Поэтому конкретное выражение для температурного поля (5) будет иметь вид:

  ^С(х, ^т) = _{£ п} ов ■ ^ехр (     / . j = _{£ п} ов ■ ^ехр (^- /.;o.⁰..j

  \ X ^(0)/

  
  
  
  
  
  

  Заметим, что из уравнения (16) следует, что при х = 0 t(x, т) = С _пов , что вполне соответствует физике процесса нагрева.

  Как видно из уравнения (16), экспоненциальное температурное поле однозначно характеризуется только одним настраиваемым параметром - ^(0), причем примечательно то, что этот параметр, вернее его числовое значение, одинаков для любого момента времени, что является достаточно привлекательным фактором. К месту заметим, что в методе парабол коэффициенты зависят от времени, они разные для разных моментов времени, при переходе от одного момента времени к другому эти коэффициенты (параметры) следует определять заново, а в методе экспонент – нет. Это обстоятельство является существенным преимуществом метода экспонент перед методом парабол.

  Однако здесь возникает вопрос о том, как определить ^(0), насколько этот метод пригоден для практического использования?

  
  

  Варианты определения начального условия ф(0)

  Здесь может быть применен следующий приближенный подход. Если считать, что t(x, т) = = С _пов ■ ехр[-^(т) ■ х|, то среднемассовая температура заготовки будет изменяться во времени следующим образом:

  £(т) = 7 /₀^Л С пов ⁽т) ■ ехр[-ф(т) ■ х| dx = -у^ехр^^т) ■ х^]| ^ = ^ ^о                                          ^ ^ (l)

  
  

  -

  
  

  ^{ехР-^тПП-Ц. ^ь ^ ^(т)

  
  
  
  

Поэтому, полагая т = 0, найдем уравнение для определения ^(0):

ё(0) = -1^ [^ехР ( -^L • ^(0)) -1] ~ ^FSr = 1 — exp ( —L • ^(0)).              (18)

^l ^(^о)                                      ^с пов ^(О)

Понятно, что это уравнение может быть решено только численным или графическим методами. Заметим, что здесь t(0) = ~^t ° (x) dx - среднемассовая температура заготовки в начале процесса.

Как показал анализ соотношения (18), в общем случае оно имеет два корня: один ^(0) = 0, второй – ненулевой, его приближенное значение находится из следующего соотношения: t(o) l ф(о) = 1 ^ ^0) = сповСо). Такой вывод вытекает из рассмотрения графиков левой и пра-WO)                t(O>L вой частей уравнения (18) (рис. 1). Для оформления рис. 1 введем следующие обозначения: у1 = едН-^0); ^2 = 1 — exp ( —L • ^(0); h = ^(0). При этом конкретно для рис. 1 L = 0,1 м; ^пов(0)

С(0) = 20 °С; С _пов (0) = 100 °С. Из рис. 1 следует, что для данного случая ^(0) = 50 м^-1.

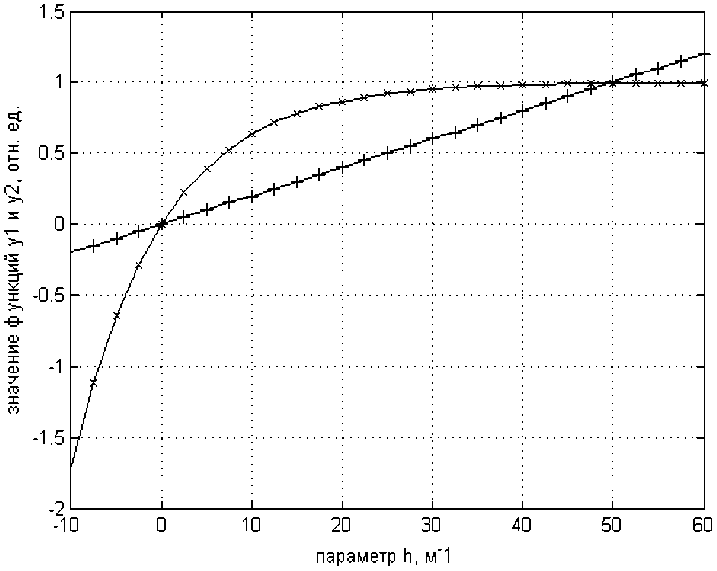
Рис. 1. Графики функций y 1 и y 2

Fig. 1. Graphs of functions y 1 and y 1

Следует заметить, что для реальных значений рассматриваемых параметров графики у1 и у 2 пересекаются при у1 = у2 = 0 и при у1 = у2 = 1. Абсцисса первой точки всегда одна и та же, это ^(0) = 0, абсцисса второй точки зависит от условий задачи ^(0) = ^(O) — это условие и может быть использовано для определения начального условия. Нулевой корень здесь не приемлем, поскольку, как это нетрудно видеть из уравнения (16), в этом случае получается, что всегда якобы C(x, т) = С _пов , что никак не соответствует физике процесса нагрева.

Вместе с тем задачу определения начального условия для функции ^(т) можно решать и так:

• 1    „L

• /^[^⁽0^)] = l^o [t⁰⁽x) — С пов • exp(—x • ^(0)}]² dx ^ тт_ф( о)/ [ф(0)].                      (19)

Здесь ^(0) следует определять из решения достаточно сложного уравнения

^OO)] = ²/о [t⁰(x) — С пов • exp (—x • ^⁽0))] • (—С пов • exp (—x • ^⁽0)) • ⁽—x)dx = 0.      (20)

Если воспользоваться начальным условием (2), то получим следующее формальное выражение для ф(0):

С⁰⁽х) = С пов • ехр(-х • ^(0)) ^ ^(0) = "ln (у^) - ^х         ^ пов '

Таким образом, из (21), во-первых, следует, что ф(0) должно иметь разное значение для различных %, только если начальное температурное поле описывается приближенно экспонентой С0(х) « Спов • ехр(^ • х), то получается, что ф(0)»-^ (здесь ft - некоторый коэффициент), а во-вторых, конкретное выражение для температурного поля будет следующим:

(   x2infR А

С(х, г) = tnoe • exp - ,0 пов7    .

\ Ц^к Т-г-х²

'       \ гпов /           '

Анализ граничных условий

Граничное условие (4) в общем случае при конечном значении времени т в принципе не может быть удовлетворено, так как ^х^ = С _пов • ехр[-ф(т) • L] • [-ф(т)] ^ 0. Однако если в процессе нагрева температура поверхности поддерживается на постоянном уровне С _пов = const, то при т ^ » по физике процесса будет так, что температура в любой точке заготовки будет равна С _пов , тогда из (5) будет следовать, что должно быть ф(т) ч 0 при т^м. Если же рассмотреть уравнение (14), то, действительно, рассматриваемая функция ф(т) этому условию удовлетворяет. Таким образом, граничное условие (4) при рассматриваемом описании температурного поля точно удовлетворяется только при т ч м.

Если же рассмотреть граничное условие (3), то здесь, как это нам представляется, проблем нет, причем удается определить температуру печи, которая обеспечивает поддержание температуры поверхности сляба на постоянном уровне:

• -Л^ = —Л • Спов • [-^(т)] = “(Сп - Спов) ч Сп(т) = Спов[1 + ^Ш (23)

Вычислительные эксперименты

Рассмотрим, какие температурные поля получаются в заготовке, если пользоваться методом экспонент. Например, будем считать, что а _Т =0,02 м- ; L = 0,05 м; t(0) = 20 °С; С _пов (0) = = 500 °С. Тогда ф(0) = уоуу = ₂₀ ⁵ °° _0S = 500 м^-1, поэтому конкретное выражение для темпера- Х^500\ турного поля, найденного методом экспонент, будет следующим: С(х, т) = 500 • ехр (- ₁₀   ).

Здесь т следует подставлять в часах.

На рис. 2 представлен график температурного поля для т = 0 ч, вычисленный по указанной формуле. Подчеркнем, что при этом считалось, что t(0) = 20 °С. Здесь соблюдается только равенство среднемассовых температур при т = 0 ч, а начальное температурное поле, каким бы оно ни было в реальности, при вычислениях представляется экспонентой. В этом заключается особенность первого варианта определения ^(0).

На рис. 3 представлены кривые распределения температуры по сечению сляба, вычисленные по методу экспонент, конкретно по формуле С(х, т) = 500 • ехр (- ^{х 500} ) для т = 0,5 ч; т = 1,0 ч;

10т+х/

т = 2,0 ч .

Как видно из рис. 3, распределение температуры по сечению практически равномерное, здесь только нужно иметь в виду, что во всех случаях Спов = 500 °С (это при х = 0), т. е. имеются особенности оформления графиков в среде MATLAB.

Далее пусть, например, С0(х) = 2,4 • 104 • х2, °С, в этом случае так же, как и в предыдущем случае для L = 0,05 м t(0) = 20 °С. Тогда для ранее указанных исходных данных конкретное выражение для температурного поля будет таким:

С(х, т) = 500 • ехр (- х In(48 х )—-).

• ^{4 7}                   1п(48^Х²>0,02т-Х²/

При этом к месту подчеркнем, что при т = 0 будет С(х, т) = 500 • ехр (ln(48 • х2)) = = 500 • 48 • х2 = 2,4 • 104 • х2, °С, т. е. заявленное начальное условие выполняется абсолютно точно.

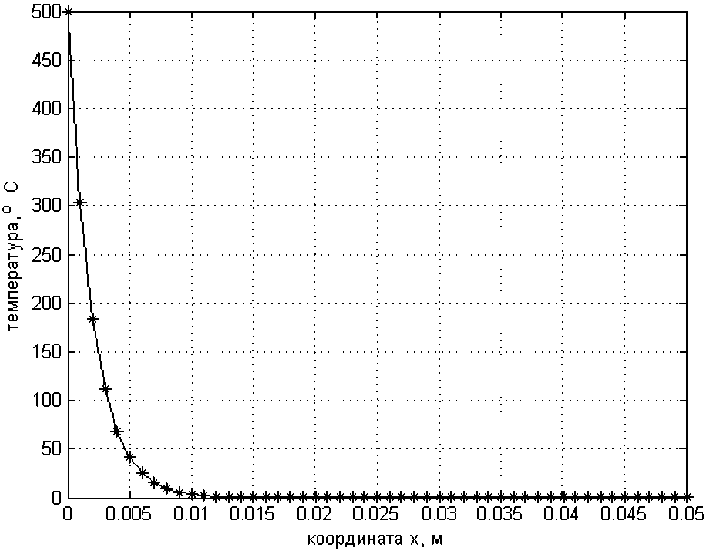
Рис. 2. График температурного поля сляба по методу экспонент при т = О

Fig. 2. Graph of the temperature field of the slab using the exponential method at т = О

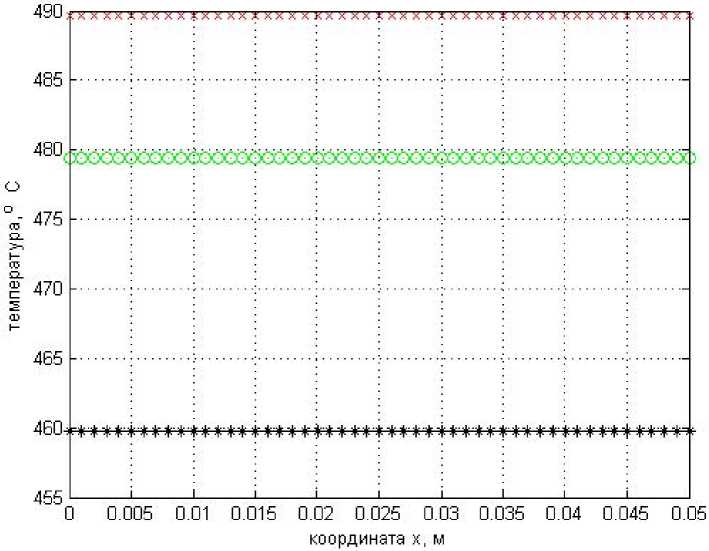
Рис. 3. Графики температурного поля сляба: при т = 0,5 ч - нижняя кривая; при т = 1, О ч - средняя кривая; при т = 2,0 ч - верхняя кривая, вычисленные для 1-го варианта определения ф(0) Fig. 3. Graphs of the temperature field of the slab: at т = 0.5 h - lower curve; at т = 1.0 h - middle curve; at т = 2.0 h - upper curve, calculated for the 1st option for determining ф(0)

На рис. 4 приведены графики распределения температуры по сечению той же самой заготовки, что и выше, вычисленные по данному уравнению, для тех же моментов времени: т = 0,5 ч; т = 1,0 ч; т = 2,0 ч . Здесь так же, как и в случае рис. 3, нужно иметь в виду, что во всех случаях tn0B = 500 °С (это при * = 0), т. е. имеются особенности оформления графиков в среде MATLAB.

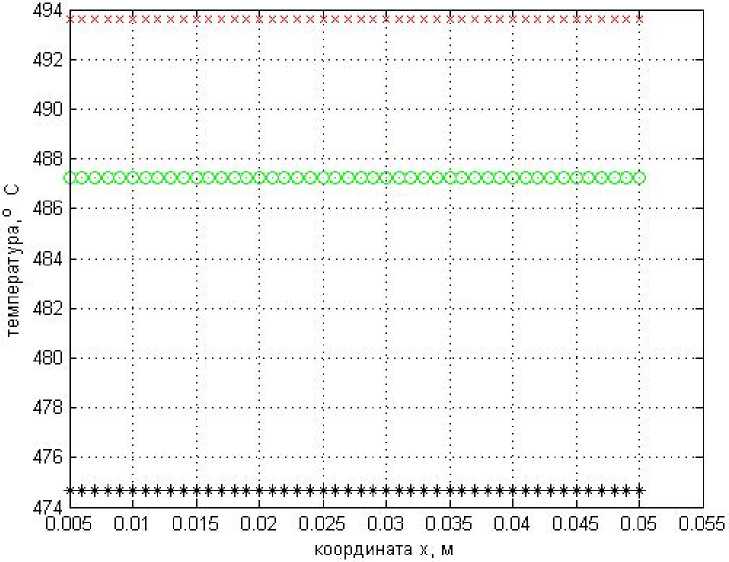
Рис. 4. Графики температурного поля сляба: при т = 0,5 ч - нижняя кривая; при т = 1,0 ч -средняя кривая; при т = 2,0 ч - верхняя кривая, вычисленные по уравнению, учитывающему точно реальное начальное температурное поле в заготовке

Fig. 4. Graphs of the temperature field of the slab: at т = 0.5 h - lower curve; at т = 1.0 h -middle curve; at т = 2.0 h - upper curve, calculated using an equation that takes into account the exact real initial temperature field in the workpiece

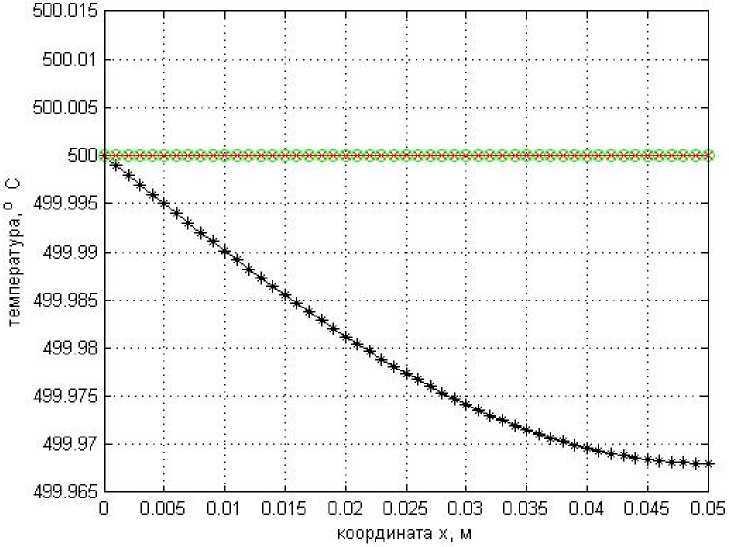
Рис. 5. Распределение температуры по сечению сляба: при т = 0, 5 ч - нижняя кривая; при т = 1,0 ч и при т = 2,0 ч - общая верхняя кривая, вычисленная по точному решению задачи нагрева

Fig. 5. Temperature distribution across the slab cross-section: at т = 0.5 h - lower curve; at т = 1.0 h and at т = 2.0 h - general upper curve, calculated using the exact solution of the heating problem

Как видно из рис. 3 и 4, точный учет реального начального температурного поля сравнительно мало влияет на результаты расчета процесса нагрева по методу экспонент, различие результатов вычислений не превышает 15 °С.

Далее для полноты исследования сравним при С _пов = const точное и по методу экспонент представления температурного поля заготовки.

На рис. 5 приведены распределения температуры по сечению заготовки для рассматриваемого случая, вычисленные по точному решению задачи методом разделения переменных, приведенному, например, в работе [4].

Следует заметить, что графики распределения температуры для т = 1,0 ч и для т = 2,0 ч практически полностью совпадают.

Таким образом, сравнивая рис. 3–5, в целом можно заключить, что с точки зрения вычисления «…важнейших температур в теле» [12, с. 110] метод экспонент можно признать приемлемым для вышеотмеченных условий.

Здесь также к месту заметим, что важнейшими в данном случае считаются температура поверхности и среднемассовая температура нагреваемого тела.

Выводы

Метод экспонент может быть применен для приближенного описания процесса нагрева, причем преимущественно в терминах «важнейших температур» – температуры поверхности и среднемассовой температуры и только для режима нагрева при постоянной температуре поверхности.