О многочленах наилучшего приближения сегментных функций

В [1] подробно изложены основы теории многозначных отображений, имеющих широкий спектр прикладных возможностей, так как использование многозначных отображений позволяет в процессе реализации алгоритма сразу оценивать погрешность приближения решения. При этом подход, разработанный автором монографии [1], не предполагает использования интервальной арифметики, что снимает вопрос о построении поля интервалов или его аналогов. Вместе с тем, теория, разработанная в [1], в значительной степени справляется с многими основными задачами интервальной математики.

(с) 2023 Трынин А. Ю.

Пусть

( ni    \/n\/ni    \/n\

U ^[a ji , b j i ^] I и I ^ x k I, I ^ [a ji , b j i ^] I П I ^ x k I = 0 , j i =0        /    \k=0 /     \ji=0        /    \k=0 /

где не пересекающиеся отрезки [aj1, bj1 ] и точки Xk принадлежат ограниченному отрезку [A, B] С R. Считаем, что функции fi и /2 непрерывны на множестве X, и всюду на X выполняется соотношение fi(x) С f2(x)- Оператор, ставящий в соответствие каждому x G X отрезок [(x, fi(x)), (x,/2 (x))], вслед за авторами работ [2-5] будем называть на X сегментной функцией F (x). В силу непрерывности функций fi и /2 сегментная функция F является h-полунеперывным отображением сверху (см. [1, § 6]). Многочлен Pm наилучшего приближения в метрике Хаусдорфа на множестве X сегментной функции F с вектором коэффициентов a = (ag, ai,..., am) G Rm+1 есть решение экстремальной за- дачи

min max max (P m (x) — fi(x),f2(x) — P m (x)) , ^a ∈ R ^m+1 x ∈ X

m

P _m (x) = ( a, ( 1, x,..., x m )) = У^ a i x i .

i =0

В случае fi = /2 задача (2) сводится к классической теореме П. Л. Чебышева для множества X .

В публикациях [2–5] приводятся необходимые и достаточные условия существования и единственности многочлена наилучшего приближения (2) для случая, когда X представляет собой либо отрезок, либо конечный набор точек. Эти работы используют методики доказательства теоремы П. Л. Чебышева и выпуклого анализа. В этом случае, даже когда X представляет собой конечный набор из n точек, количество систем, которые необходимо решить для поиска многочлена степени m , растет как C m⁺² . Кроме того, многочлен, наилучшим образом приближающий сегментную функцию, одновременно представляет собой многочлен наилучшего приближения некоторой классической функции. А из результатов исследований в работах [6, 7] следует, что независимо от метода решения задачи (2) его численная реализация возможна только для небольших степеней и хороших функций, так как модули коэффициентов многочленов наилучшего приближения непрерывных функций с ростом степени многочленов могут расти быстрее геометрической прогрессии. Тем не менее в данной работе предложен другой подход к изучению этой проблемы на основе классического анализа и теории функций. Здесь приведен также ряд примеров численных экспериментов, позволяющих убедиться в конструктивности предложенного метода исследований.

• 2.    Основной результат

Определим функцию ограниченной вариации на [A, B] :

x

, . f                                   х      1, при x G X,

^^x)=A' ^X(i) d^{4 +} X k C x ^{1 где x}<^x' = (o, при x G [A,B] \ X, ⁽³⁾

где X определено в (1), и будем рассматривать ее как меру в интеграле Стилтьеса. Сделав обозначение

R(a,x,m,f) = jm a,xi - f1(x) + f2(x), i=0

для каждого p G N определим систему уравнений

B j xi ^R(a, x, m, f) arctg (pR(a, x, m, f)) +^2^x

A

fi(x)) p-

pR (a, x, m, p ² R (a, x, m, f )

x ^ arctg (pR(a, x,m, f)) +

) d^(x) = 0, i = 0,..., m, )2 + iy относительно неизвестных a G Rm+1. Обозначим через Ep замыкание множества решений системы (4) при каждом p G N и

∞∞

E= n uE p .

k =1 p=k

Теорема 1. Для любых непрерывных на X функций fi(x) С f2(x) существует многочлен наилучшего приближения (2) в хаусдорфовой метрике h -полунепрерывной сверху на множестве (1) сегментной функции F (x) . Он единственен тогда и только тогда, когда множество (5) одноточечное в R ^{m +1} . Любой вектор a G E имеет координаты, являющиеся коэффициентами многочлена наилучшего приближения.

<1 Ввиду того, что для произвольной функции g G C[Y] справедливо соотношение lim g(x) 2 arctg (pg(x)) = |g(x)|, p→∞   π из которого следует (см., например, [8, гл. 1, § 3]) равенство

B ¹

plimo ^/ {g(x)2 arctg(pg(x))^ d^(x)^   =vraymax|g(x)| = IlgHc[y], величина уклонения многочлена Pm от сегментной функции F в метрике Хаусдорфа на множестве X может быть представлена следующим образом:

B

P(F ,P m

< R(a, x,m, f ) — arctg (pR(a, x,m, f))

f2(x) - f1(x) )²p , , Л 2p +2d^^(x) . (6)

Подынтегральная функция, как сумма (возможно нестрого) выпуклых функций с неотрицательной второй производной, в (6), как функция переменных a i , является выпуклой (возможно нестрого) на R ^{m +1} . Поэтому при каждом p G N множество векторов коэффициентов экстремальных многочленов таких, что подынтегральная функция наименее уклоняется от нуля по норме пространства L ^{2 p} [X] , является, в силу необходимого условия экстремума, множеством решений систем

B

< R (a, x,m, f)—arctg (pR(a, x,m, f))

A f2(x) - f1(x) )2p,       21 n n             m

+^--------z d^(x) I = 0, i = 0,..., m, (7)

или эквивалентных системам (7) систем (4). Непустота множества решений этих систем следует из необходимого условия экстремума, непрерывной дифференцируемости неотрицательной подынтегральной функции по всем переменным и ее неограниченного возрастания по любому направлению пространства R ^{m +2} при стремлении аргумента к бесконечности.

Так как функции f1 и f2 непрерывны на множестве (1), то предельный переход в интеграле Стилтьеса обосновывается с помощью теоремы 2 из [9, гл. 8, § 7].

Коэффициенты экстремальных многочленов, наименее уклоняющихся от сегментной функции F(x) в метрике Хаусдорфа, в силу замкнутости множества нулей непрерывной функции составляют множество (5) точек прикосновения всевозможных пределов подпоследовательностей решений систем (4).

По теореме Кантора [8, гл. 5, § 1] множество (5) не пусто. >

• 3.    Результаты некоторых численных экспериментов

В этом параграфе приведем результаты численных экспериментов, организованных с помощью утверждения теоремы 1. Решение систем (4) осуществлялось с помощью некоторой адаптации стандартных методов наискорейшего спуска или покоординатного спуска к решению изучаемой экстремальной задачи. На рисунке 1 изображена реализация примера, демонстрирующего, что рассматриваемый многочлен первой степени наилучшего приближения отличается от Чебышевского наилучшего приближения середин отрезков сегментной функции. На рисунке 2 график одного из многочленов двенадцатой степени наилучшим образом аппроксимирущих в метрике Хаусдорфа ту же сегментную функцию, что и на рисунке 1.

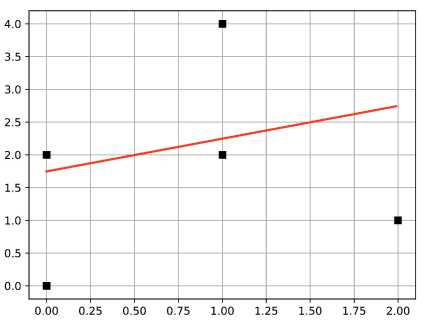
Рис. 1. n = 2, m = 1.

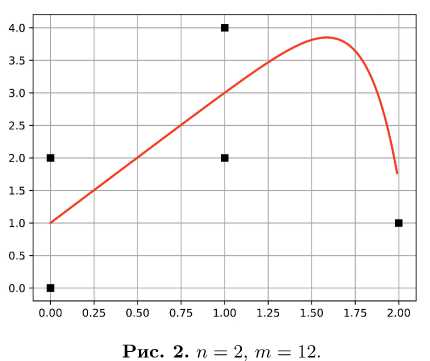
Рис. 3 демонстрирует возможность предлагаемого метода обрабатывать большие массивы данных. В качестве модели сегментной функции рассматривается пара f 1 (x k ) = sin7x k — 1 , f ₂ (x k ) = sin7x k + 0.1x k + 1 , где 0 <  k <  1000 . В качестве многочлена наилучшего приближения взята линейная функция.

Еще один очевидный пример наилучшего Хаусдорфова приближения сегментной функции fi (x k ) = sin X k — 1 , f ₂ (x k ) = sin X k + 1 , где 0 ^ k ^ 3 , многочленом первой степени, который вычислен с помощью теоремы 1, приведен на рис. 4.

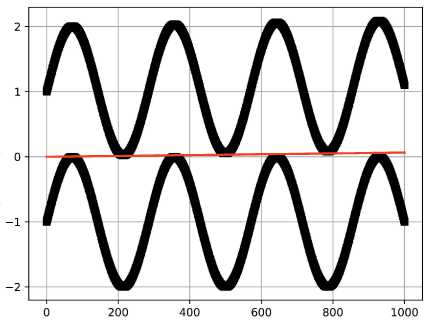
Рис. 3. n = 1000, m = 1.

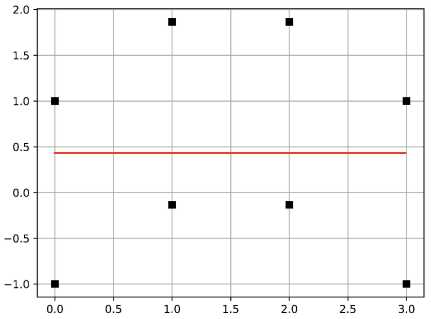
Рис. 4. n = 3, m = 1.

Рис. 5 содержит график реализации приближения сегментной функции F(0) = [(0,1), (0,1)], F(1) = [(1, 0), (1, 2)] многочленами наилучшего Хаусдорфова приближения первого порядка, которые вычислены с помощью теоремы 1 два раза. Это та ситуация, когда многочлен наилучшего приближения не единственен. В этом случае множество E представляет собой отрезок [(2, — 1), (0,1)]. Адаптация метода наискорейшего спуска, о которой шла речь в начале этого параграфа, позволяет приближенно вычислять коэффициенты многочленов наилучшего приближения с границы множества E, выбирая различные начальные итерации. Графики двух таких многочленов и получены в результате описанного численного эксперимента.

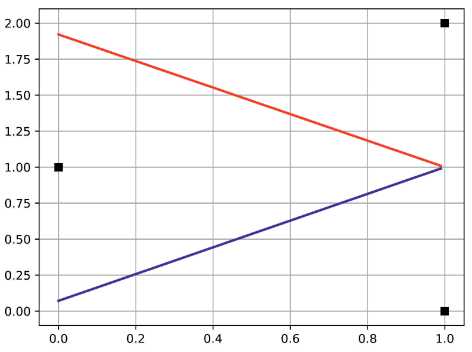
Рис. 5. Многочлены с коэффициентами с границы множества E , n = 1, m = 1.