О моделировании динамических процессов в сферических и цилиндрических оболочках

просто с численными методами. В [1–4] показано, что в то время когда адиабатическое ядро законов сохранения порождает следствие — сохранение энтропии вдоль траектории частиц, «адиабатическое ядро» разностных законов сохранения порождает изменение энтропии. Следствием этого является различие между точным решением задачи и численным решением при конечных шагах сетки.

Другим источником погрешности результатов математического моделирования служит погрешность физической модели А _Ф . Она складывается из погрешностей: уравнения состояния; зависимости между компонентами девиатора тензора напряжений и девиатора тензора деформаций; способа моделирования метастабильных состояний (области отрицательных давлений, упругих сдвигов, полиморфных переходов, плавления и испарения). Различие между погрешностями двух физических моделей |А _ф 1 -А _{Ф 2}| может быть надежно определено с помощью расчетов лишь в том случае, когда погрешность алгоритма А М много меньше этого различия |А _м |«|А _ф 1 - А _{Ф 2}| .

В случае идеальной среды и гладких течений погрешность математического моделирования неустановившихся течений сплошной среды удобно исследовать на примере энтропии, которая в такой физической модели остается постоянной вдоль траектории движения каждой частицы. Поэтому отличие ее расчетных значений от начального значения может быть использовано для анализа индивидуальных достоинств и недостатков конкретного численного метода. Но при другой физической модели в частности в реальных пластических течениях, которые, как известно, необратимы, энтропия изменяется. Таким образом, использование энтропии в качестве критерия точности позволяет разделить вклады, вносимые в погрешность математического эксперимента разностным методом и физической моделью.

Исследования нескольких моделей пластического течения, проведенные в 1973 году [5], показали, что характерные для них величины диссипации энергии различаются слабо. Однако с тех пор положение в математическом моделировании сплошных сред существенно изменилось. Появились новые численные методы и новые модели упругопластического деформирования, а значит, изменилось соотношение между А _М и А _Ф .

Рассмотрим частную задачу определения точности численного моделирования динамических процессов в оболочках несколькими разностными методами с применением разных моделей пластичности.

• 2.    Основные уравнения

Физические процессы в сферически или цилиндрически симметричных оболочках описываются системой законов сохранения массы, количества движения и энергии. Из этих законов с помощью формальных преобразований получается ряд следствий. Вместе с исходными уравнениями они образуют переопределенную систему, в которой независимыми являются только три уравнения. Наиболее часто в качестве независимых выбираются уравнения неразрывности, движения и внутренней энергии:

1 dV 5U (а-1)U _ о

• V    dt 5 rr

1 dU /I P - S 1 ) ( а- 1 )( S 1 - S 2 )„ 1_ о

• V    dt      5rr

• 1    dE P dV _V U U u^U ( а- 1 ) --+ _ S 1 + S 2—   -.

• V    dt V dt     5 rr

Здесь U — радиальная скорость, V — удельный объем, E — удельная внутренняя энергия, r — расстояние от центра (оси) симметрии, α — показатель симметрии (α имеет, соответственно, значение 1, 2 или 3 в случае плоской, цилиндрической или сферической симметрии). В уравнении движения (2) и уравнении внутренней энергии (3) главные напряжения σ _i , представляются в виде разности девиатора S_i тензора напряжений и давления Р (шаровой части тензора напряжений): о i = - Р + S i , S 1 + S 2 + S 3 = 0. Вводя наибольшие касательные напряжения т 1 = 0,5 ( S 2 - S 3 ) , т₂ = 0,5 ( S 3 - S 1 ) , т₃ = 0,5 ( S 1 - S ₂ ) и соответствующие деформации сдвига у 1 = £ 2 - £ 3 , у ₂ = £ 3 - £ 1 , у ₃ = £ 1 - £ 2 , запишем уравнение (3) в следующем виде:

dE + pdv - 2 у d    = 0

dt dt 3 7= 1    dt

Удельную внутреннюю энергию E представим в виде суммы

E = ET + EX + ЕУ , где EХ — холодная энергия, равная сумме энергии потенциального взаимодействия атомов и энергии их нулевых колебаний, EТ — тепловая энергия, EУ — энергия упругих сдвигов. Деформации сдвига также представим в виде суммы упругих уe и пластических yf деформаций:

• У , =Y ^e +Y ^f .

Поскольку Р = Р Т + Р Х , то согласно с работой [6] запишем уравнение (4) в виде уравнений для тепловой, холодной и упругой энергий:

E + p_r dV - 2 у d т , < = 0, dt dt 3 “1    dt

dE+p dV=0, dt dt dEУ dt

3 e

— vy т,- — = 0.

3 ^d dt

Из (6) следует выражение для касательных напряжений в области упругих деформаций

3 5Ey т,- =----.

¹   2V 5y ie

Из сравнения уравнения (5) со следствием основного уравнения термодинамики dET + p dV - TdS = 0 dt Т dt dt видно, что изменение энтропии определяется работой касательных напряжений на пластических деформациях сдвига

T^ = 2 V у T d_I p dt 3 t1 i dt

Уравнение (7) означает, что в случае, когда компоненты девиатора тензора напряжений равны нулю (тi — 0), уравнение для внутренней энергии имеет вид dE dV

— + P— dt dt и энтропия сохраняется вдоль траектории частицы dS—о.

dt

• 3. Численные методы

В работе [1] показано, что при замене трёх исходных независимых дифференциальных уравнений разностными погрешности аппроксимации ω определяют производство энтропии:

TdS M — _Ю .

dt

Одним из важных требований, предъявляемых к разностной схеме, является требование, чтобы энтропия S М была меньше физической энтропии S Ф , определяемой конкретными физическими процессами. С этой точки зрения и рассмотрим, следуя [1–3], производство энтропии в разностной схеме адиабатического ядра [4] системы уравнений механики сплошной среды (1)–(3):

dV dt

r

а- 1

5 U (а-1) UV

~---= Ю1, о m     r

dU

----+ r ^{а 1}

dt

5P

— м7, 5 m

dE dV

— + P--— №., dt dt а-1

где m — лагранжева массовая переменная ( dm — р r dr, p — плотность среды внутри оболочки). Номера у погрешностей аппроксимации ω k взяты в соответствии с [3]. В [2] показано, что для предложенного в [7] разностного уравнения внутренней энергии

E^{n + 1} - Eⁿ + 2 ( P^{n + 1} + Pⁿ )( V^{n + 1} - Vⁿ ) — 0

уравнение производства энтропии имеет вид

_T dS_M dt

т ² (

д ² P

¹² (^д V 2 J S

Поскольку все величины в выражении (9) относятся к одному сеточному интервалу с номером i - ( 12 ) , то для простоты здесь и далее нижний индекс будем опускать, оставляя верхний индекс n , отвечающий временному шагу.

Подставив производную dV dt из (8) в (10), запишем уравнение производства энтропии следующим образом:

_T dS M dt

т ² ( д ² P

12 (д V

J f r .- , а и + ( а^- 1 ) ^UV J

J S (    дm      r J

⁺ O ^{( т} 3 ) .

В сходящейся оболочке (внутренний радиус r ^ 0) радиальная скорость течения

U ^ -да и, таким образом, в некоторой массе вещества, примыкающего к внутренней границе, и при

энтропия может возрастать. В расходящейся оболочке r возрастает, U >  0 ,

д U

--> д m

энтропия, определяемая погрешностями аппроксимации

дифференциальных уравнений разностными, со временем убывает.

В методе Неймана–Рихтмайера [7], который широко применяется в вычислительной механике сплошных сред, разностное уравнение для внутренней энергии в дифференциальной форме имеет вид dE

— + dt

dV

⁽ P ⁺ q ) "th

= Ю 7 .

Величина q является псевдовязкостью. Она выбирается из различных соображений, но всегда так, чтобы для непрерывных течений выполнялось условие: q = 0 . Авторы этого метода в разное время рекомендовали три формы записи псевдовязкости [7–9]:

Р

kh ²

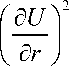
д U n при---< 0, д r д U^n при---> 0, д r

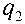
kh ² f dV \ V ( dt J

dV при---< 0, dt dV при---> 0, dt ,

k (h0 )2 f dVJ2 f r^V(a 1) V ( dt J ( r J dV при---< 0, dt dV при---> 0, dt

где h = рА r — «плоская» масса сеточного интервала в момент времени t ; k — безразмерная эмпирическая постоянная; величины с индексом «0» отнесены к начальному моменту времени.

Разностный аналог уравнения (11) в соответствии с [7] записывается в следующем виде:

E

n + 1

En + - (Р

+ P ⁿ + 2 q ^{n + 1} )( V ^{n + 1} - V ⁿ ) = 0 .

Это уравнение вместе с произвольным уравнением состояния Р = Р ( V , E ) образует нелинейную систему двух уравнений, решение которой при заданном V" ^{+ 1} находится посредством итераций.

Кроме метода Неймана–Рихтмайера для получения численного решения использовался также метод Куропатенко [10, 11], в котором уравнение для внутренней энергии в случае непрерывного решения записывается в виде

En+i - En + J р ( v, e ) dv = о

Vn и в последующем интеграл заменяется суммой, от числа слагаемых в которой и зависит точность определения энтропии.

В [10, 11] для разделения разрывных и непрерывных решений используется знак разностной производной скорости среды , где А U = U ( r + А r ) - U ( r ) . Если ^^ > 0 ,

А r                v            v /         а r то считается, что решение непрерывно. Если же

А U а — < 0,

А r

то предполагается, что

в сеточном интервале на одном шаге по времени распространяется ударная волна, обеспечивающая диссипацию энергии. Критерий, основанный на анализе знака

А U отношения    , не точен, так как при его использовании решения, в которых энтропия

А r должна сохраняться без изменения, могут попадать в разряд диссипативных решений.

Это можно показать на примере уравнения (1), если записать его в виде

d U = 1 dV (а-1) U dr V dt r dU

Условие --- < 0 допускает такие решения, которые при U > 0 удовлетворяют

5 r условию

_А 1 dV ( а- 1 ) U 0 <--< -^----—

.

Vdt r

Это означает, что хотя траектории любых двух точек внутри оболочки и сближаются

, 5U

• (--- < 0), плотность течения уменьшается. Включение в таких ситуациях сеточного

5 r диссипативного механизма является источником искусственных погрешностей.

Для предотвращения влияния этого источника диссипации энергии процесс определения

d U a термодинамических величин в случае---< 0 разделяется на два этапа.

• 5 r

На первом этапе, исходя из уравнения dV (а1)UV dt

r

рассчитывается удельный объем V * . Независимо от знака U значение V * находится с помощью уравнения tn+ (а-1)UV

• V* _ Vn + [ (-----)----dt.

• 4.    Постановка расчетов

t n          r

На втором этапе для полученного значения V ^* по уравнению изэнтропы (16) и уравнению состояния P = P(V, E) находятся термодинамические величины P ^*, E ^* [11].

Поскольку < 0, то вещество с параметрами P*, V*, E* испытывает ударное 5 r нагружение в соответствии с «сеточной» ударной адиабатой. В итоге находятся окончательные значения Pn+1, En+1, отвечающие значению Vn+'. Использование «сеточной» ударной адиабаты обеспечивает необходимую диссипацию энергии.

Описанный выше алгоритм двухэтапного расчёта термодинамических величин в сеточном интервале реализован в программном продукте ВОЛНА [12].

Для описания свойств шаровой части тензора напряжений используется простейшее уравнение состояния конденсированного вещества

P _(y- 1 ) р E + C 0k ( р-р„„ ) ,                                                     (17)

где у — безразмерная постоянная величина; р _{0 к} и C _{0 к} — теоретические значения кристаллической плотности и соответствующей скорости звука (в  точке

.                          р         P

P _ 0, T _ 0, E _ 0). Переход к безразмерным переменным--> р, ----^—> P, р0 к          р0 kC0 к

EU

—2— > E ,-- > U в уравнении (17) приводит его к виду

C 0² k          C 0 k

P _(у- 1)рE + р-1.

Принимается еще одно упрощение, а именно, полагается у _ 3 , что близко к значению y для большого числа реальных сред.

Давление P и удельная внутренняя энергия E представляются в виде сумм, P = P X (ρ) + P T (ρ, S ), E = E X (ρ ) + E T (ρ , S ), где холодные и тепловые составляющие P и E имеют вид

P v = 3 ( p 3 - 1 ) . E, = 1 p 2 + -1- - 1, X 6    3 p 2

P t = 3 f ( s ) p 3 ,                                       (19) E t = 6 f ( s ) p 2 .                                       (20)

Значение энтропийной функции     f ( S ) ,    характеризующее отклонение

от изоэнтропического течения, рассчитывается по формуле

3(2 Ep + p-1 +1 f (s) = ( p p )

P

В методе Неймана–Рихтмайера уравнение (15) дополняется уравнением состояния (18) в виде

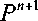
'3 n + 1 Т7 П + 1 I n + + 1     1

= 2p E +p -1

и из соотношений (15) и (22) исключается P ^{n + 1}. В результате получается зависимость

n + 1           n n        n + 1

E от E , p и p :

E n ^{+ 1} = aEⁿ + b + c ,

где

= _p^ ( 4 p ^{n 1 1} - 2 p ⁿ ) a p ^{n + 1} ( 4 p ⁿ - 2 p ^{n + 1} ) ,

n + 1 nn\( n+ + 1 , nn О \ _{b =} p ^-p ⁾⁽ p +p^-2) _n +1 / n       3_ n +1 \

p (4p - 2p )

n + 1 nn \

c=— p -p)

° p ^{n + 1} ( 4 p ⁿ - 2 p ^{n + 1} ) .

После определения E ^{n + 1} давление P ^{n + 1} рассчитывается по уравнению состояния (22), а энтропийная функция — по формуле (21), в которой все величины берутся в момент t^{n + 1}:

f ( s ^{n + 1} ) =

3 ( 2 E ^{n + 1} p ^{n + 1} +p ^{n + 1} - 1 ) + 1

Таким образом, в методе Неймана–Рихтмайера энтропия изменяется при изменении плотности ρ даже в случае, когда q = 0. Этот теоретический результат далее подтверждается практически с помощью расчетов сходящейся сферически симметричной оболочки с безразмерным уравнением состояния (18).

При t = 0 безразмерные характеристики задачи таковы: радиус внутренней границы оболочки (ВГО) г_ВгО = 1, радиус наружной границы оболочки (НГО) г_НГО = 1,1;

p, P, E постоянны и равны: р = 1, P = 0, E = 0. Скорость среды в оболочке задана так, dV чтобы при t = 0 выполнялось условие---= 0. В таком случае из (1) следует: dt д U ) (а-1) U ---I +------— = 0.

5 r ) t        r

Интегрирование этого уравнения приводит к следующему выражению для U ( r ) при t = 0 :

U = U ВГО

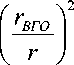
При t > 0 на внутренней и наружной границах оболочки задается условие P = 0 (иными словами, рассматривается инерционное движение оболочки). Расчеты выполнены для трех оболочек, различающихся безразмерной начальной скоростью ^{( U} _ВГО =^{- 0,1; - 1; -} 5).

Следует заметить, что в оболочках, разгоняемых продуктами взрыва, скорость течения близка к звуковой: U_ВГО « - 1. При воздействии на оболочки излучения

(например, лазерного) скорость существенно сверхзвуковая UВГО =-7 ^-15. Такое разделение оболочек на «тихоходные» и «быстроходные», или «дозвуковые», «звуковые» и «сверхзвуковые», является условным, так как при схождении оболочек Uвго (t ) >-^ при гВГО (t ) ^ 0 и, таким образом, любая оболочка рано или поздно становится сверхзвуковой (по крайней мере, в окрестности ВГО). В процессе движения сходящейся оболочки с заданным начальным профилем скорости (23) профиль скорости в каждый фиксированный момент времени t* — U (r, t*), является монотонным и дU удовлетворяет условию --> 0. В то же время профиль давления имеет немонотонный

5 r характер. Максимальное давление достигается внутри оболочки в точке rmax , и при уменьшении гвго расстояние rmax - гвго сокращается, обращаясь в нуль при гвго = 0 .

Далее приводятся результаты расчетов, выполненных по методу Неймана– Рихтмайера с использованием трех форм псевдовязкости (12)–(14) и по методу Куропатенко [10] с учетом введенных выше изменений. Далее этот метод будет называться методом «ВОЛНА», поскольку для расчетов использовался программный комплекс [12] с одноименным названием.

• 5.    Результаты расчетов

В первой серии расчетов рассматривалось течение идеальной ( S 1 = S 2 = S 3 = 0) конденсированной среды, описываемой уравнением состояния (18). Начальная плотность среды р = 1 . Для дискретизации расчетной области во всех вычислительных экспериментах использовалась равномерная по радиусу сетка с числом интервалов 200. Решаемая тестовая задача сформулирована так, что при нулевом девиаторе тензора напряжений в оболочке от начала движения до момента фокусировки ( г_вго ( t ) ^ 0) выполняются условия: P T = 0; E T = 0; f ( S ) = 0 .

Таблица 1. Средние и максимальные значения плотности и энтропийной функции, полученные в гидродинамическом приближении

Метод вычисления	Начальный профиль скорости
	дозвуковой U ВГО = - 0,1				звуковой U ВГО = - 1				сверхзвуковой U ВГО = - 5
	P cp	P max	f cp	f max	P cp	P max	f cp	f max	P cp	P max	f cp	f max
q 1	1,0188	1,453	2,616 ∙10-8	4,706 ∙10-6	1,2702	4,269	2,143 10-5	3,030 ∙10-3	2,6082	13,539	1,909 ∙10-4	1,760 ∙10-2
q 2	1,0186	1,384	4,734 ∙10-4	6,740 ∙10-2	1,2622	2,806	2,720 ∙10-2	4,409	2,5399	7,289	0,119	21,020
q 3	1,0187	1,412	2,547 ∙10-4	4,068 ∙10-2	1,2654	3,057	2,180 ∙10-2	3,883	2,5627	8,206	6,72 ∙10-2	12,154
ВОЛНА	1,0188	1,453	3,670 ∙10-12	1,483 ∙10-10	1,2702	4,270	4,644 ∙10-13	1,430 ∙10-10	2,6082	13,552	1,008 10-12	1,181 ∙10-10

В таблице 1 приведены средние и максимальные значения энтропийной функции f ( S ) в момент фокусировки сферической оболочки, соответствующие трем различным начальным значениям U ВГО . Среднее значение f ( S ) определялось по формуле

N fcp = ^ f (S) Mi M , где N — число интервалов сетки, f (S), Mi — значение i=1 / энтропийной функции и масса вещества в сеточном интервале с индексом i, M — масса оболочки. Как видно из таблицы, метод ВОЛНА позволяет найти средние и максимальные значения энтропийной функции с высокой точностью. Можно считать, что версия метода Неймана–Рихтмайера с вязкостью q1 (формула (12)) также дает удовлетворительные значения энтропийной функции для всех трех оболочек. В случае использования вязкостей q2 и q3 (формулы (13) и (14)) энтропия определяется неудовлетворительно. Переход с нулевой изэнтропы на ненулевую чреват тем, что возникающие в веществе фазовые переходы будут рассчитываться неверно.

Таблица 1 содержит также средние и максимальные значения плотности среды в момент фокусировки оболочки. Расчеты показывают, что для «дозвуковой» и «звуковой» оболочек средние плотности, вычисленные различными методами, близки, а различия в значении максимальной плотности достигают 4,7% для «дозвуковой», 34,3% для «звуковой» и 46,2% для «сверхзвуковой» оболочек. Такие результаты объясняются тем, что при уменьшении с течением времени радиуса ВГО погрешности аппроксимации в окрестности внутренней границы возрастают сильнее, чем во всей оболочке. Это приводит к росту энтропии в соответствии с уравнением (10), что вызывает уменьшение сжатия, то есть снижение плотности.

Максимальные значения вклада теплового давления (см. (19)) в полное давление

v =

P T

P X + P T

и вклада тепловой энергии (см. (20)) в полную энергию

Ц =

ET

E T + E X

представлены в таблице 2.

Таблица 2. Максимальный вклад теплового давления и тепловой энергии в полное давление и полную внутреннюю энергию

Метод вычисления	Начальный профиль скорости
	дозвуковой UВГО = - 0,1		звуковой UВГО = - 1		сверхзвуковой UВГО = - 5
	V max	Ц тах	V max	Ц max	V max	Ц max
q 1	6,979∙10-6	2,0350∙10-5	0,00306	0,0035	0,0173	0,0176
q 2	9,770∙10-2	2,6360∙10-1	0,82400	0,7400	0,9550	0,9043
q 3	5,930∙10-2	1,6480∙10-1	0,80100	0,6454	0,9240	0,8326
ВОЛНА	8,362∙10-7	9,9733∙10-8	4,568∙10-8	3,4465∙10-14	1,746∙10-9	6,8395∙10-15

Следует заметить, что в точном решении задачи v = 0, ц = 0 . Из таблицы видно, что метод Неймана–Рихтмайера [7] с псевдовязкостями q ₂ и q ₃ даёт неудовлетворительные результаты. Завышенные значения ν и μ коррелируют с завышенными значениями f ( S ) и заниженными значениями плотности. В «дозвуковой» оболочке максимальные значения ν и μ достигают значений ~0,098 и 0,264; в «звуковой» и «сверхзвуковой» оболочках они неприемлемо высоки и достигают значений v max ~0,955, ц max ~0,904.

В первой серии расчетов определены различия в получаемых результатах, связанные с применением разных вычислительных алгоритмов — методические различия в случае одной и той же физической модели — идеальной жидкости. Чистота сравнения обеспечена таким выбором начального состояния и граничных условий оболочки, при котором от начала динамического процесса в оболочке вплоть до её фокусировки точное решение имеет вид P T = 0, E T = 0, f ( S ) = 0.

Во второй серии расчетов та же самая задача рассмотрена с добавлением в уравнения движения и энергии не равного нулю девиатора тензора напряжений. Процессы в оболочке описываются в рамках моделей упругости (законом Гука с постоянным модулем сдвига) и пластичности (моделью идеальной пластичности [13]). Принято: коэффициент Пуассона v = 0,22 ; безразмерный модуль сдвига G = G /( р₀ C 2 ) = 0,510; безразмерная величина предела текучести Y = yJ ( р ₀ C ₀ ² ) = 0,006 ; число интервалов по радиусу 200.

В таблице 3 приведены результаты расчетов параметров среды на момент окончания процесса течения. Для оболочки с U ВГО = - 0,1 — это время поворота ВГО, для остальных оболочек — время фокусировки. Следует отметить, что при снижении U_ВГО уменьшается начальная кинетическая энергия оболочки и возрастает время фокусировки. В гидродинамическом приближении время фокусировки всегда конечно при | U ВГО < 0 и стремится к бесконечности при U ВГО ^ 0. В оболочке же с реальным веществом, имеющим отличный от нуля девиатор тензора напряжений, время фокусировки стремится к бесконечности при U ВГО ^ -0,12037. При последующем увеличении безразмерной начальной скорости оболочки U_ВГО скорость ВГО обращается в нуль при некотором конечном значении радиуса ВГО в момент t_ост (оболочка останавливается, не сфокусировавшись). Значение t_ост зависит от U_ВГО таким образом, что t_ocm стремится к нулю при U ВГО ^ 0 .

Таблица 3. Средние и максимальные значения плотности и энтропийной функции, полученные с использованием модели идеальной пластичности

Метод вычисления	Начальный профиль скорости
	дозвуковой		U ВГО =	- 0,1	звуковой UВГО = - 1				сверхзвуковой UВГО			= - 5
	р cp	Р max	f cp	f max	р cp	р max	f cp	f max	р cp	р max	f cp	f max
q 1	0,9946	0,997	0,0249	0,0329	1,2431	6,078	0,04950	0,211	2,5584	17,621	0,0298	0,177
q 2	0,9946	0,997	0,0249	0,0329	1,2392	3,534	0,05833	10,890	2,5311	9,364	0,0540	29,170
q 3	0,9946	0,997	0,0249	0,0329	1,2405	3,831	0,05618	8,756	2,5422	10,981	0,0436	17,278
ВОЛНА	0,9945	0,997	0,0252	0,0329	1,2431	6,093	0,04949	0,176	2,5584	17,668	0,0298	0,139

Таблица 3 содержит средние и максимальные значения плотности вещества и энтропийной функции f ( S ') для «звуковой» и «сверхзвуковой» оболочек в момент фокусировки, а также для «дозвуковой» оболочки в момент остановки ВГО. Видно, что независимо от метода вычисления средняя и максимальная плотности среды в остановившейся оболочке меньше, чем в исходном состоянии ( р = 1 ). Причиной этого является физическая диссипация энергии в пластическом течении вещества, заполняющего оболочку. Методическая (математическая) диссипация энергии заметно сказывается лишь на максимальной плотности «сверхзвуковой» оболочки, отличия значений которой друг от друга достигают 47%, в то время как значения средних плотностей отличаются на ~1%.

В оболочке с начальной скоростью U ВГО = - 5 средняя плотность оказалась почти в 2 раза выше, чем в оболочке с U ВГО = - 1. В то же время среднее значение энтропийной функции здесь заметно меньше. Объяснение такого поведения функции f ( S ) можно получить, оценив диссипацию энергии на пластических деформациях.

По определению

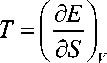
Поскольку E_X не зависит от S , то из (20) и (24) следует выражение

T = 1 ,. dfM .

6 dS

Подстановка T в левую часть уравнения (7) дает уравнение для определения f ( S )

d №) = 4V з f т &.

dt м ¹ dt

В модели идеальной пластичности при Y = const главные касательные напряжения и скорости деформации сдвига имеют вид

Т= 0,    т₃=-т₂= 0,5Y ,   d^ — 0,   d ^ ³

1      32         dt      dt

d у 2 _d U U

.

dt     d r   r

Подстановка (26) в (25) приводит к выражению

df (5 )-4   ( dV 3UV )

.

dt V dt r )

Среднее значение энтропийной функции для оболочки в момент фокусировки t_Ф следует из (27):

1M tФ f ф — — f f 4YV2 ср

M 00

dV

dt

3 UV

dtdm .

r

Если к (28) дважды применить теорему о среднем, получится уравнение для fсфр f ф — 4 Y ср

V ³ t_Ф

V 0 ³

v

ЩИ*

*       t Ф

r

)

где U — U ( t , m ) , ( V ) — V ( t , m ) , r — r ( t , m ) , 0 <  m <  M и 0 <  t <  t_Ф — некоторые промежуточные значения величин. Их замена следующими приближенными соотношениями

1 Ф 00

НГО НГО ВГО ,

_{2 t Ф} НГО НГО ВГО

(V3 )■—I ((V Ф )3+(V ° )3) •

1 Ф 00

НГО НГО ВГО 4

позволяет вычислить значение энтропийной функции в момент фокусировки. Отсюда следует, что / ф — 0,0349 для оболочки с U ВГО —- 1 и / ф — 0,0236 для оболочки с U ВГО — - 5. Несмотря на грубые приближения, эти оценки точно передают порядок величины среднего значения энтропийной функции и отличаются от соответствующих значений, полученных методом ВОЛНА, соответственно, на ~30% и ~20% (Табл. 3).

Таким образом, с уверенностью можно говорить, что в быстроходной оболочке пластичность влияет на состояние вещества слабее, чем в тихоходной оболочке.

Из таблицы 3 следует, что в момент фокусировки максимальное значение энтропийной функции f_cp , определяемой пластическим течением, достигается в расчетах по методу Неймана–Рихтмайера с вязкостью q 2 Оно отличается от минимального значения f_cp , полученного по методу Куропатенко, на величину 0,00884 для «звуковой» оболочки и на величину 0,0242 для «сверхзвуковой» (7-й и 11-й столбцы, Табл. 3). В то же время различия значений f_cp , обусловленные выбором метода решения

Таблица 4. Среднее значение удельной тепловой энергии E_T в зависимости от предела текучести Y

Метод вычисления Начальный профиль скорости дозвуковой UВГО = -0,1 звуковой UВГО = -1 сверхзвуковой UВГО = -5 Y = 0,006 Y = 0,004 Y = 0,006 Y = 0,004 Y = 0,006 Y = 0,004 Среднее значение удельной тепловой энергии q1 0,00411 0,00411 0,0181 0,0123 0,0797 0,0550 q2 0,00411 0,00411 0,0223 0,0170 0,1362 0,1184 q3 0,00411 0,00411 0,0226 0,0173 0,1380 0,1189 ВОЛНА 0,00415 0,00412 0,0180 0,0122 0,0778 0,0529 в гидродинамическом приближении, оказываются большими: 0,0272 для «звуковой» и 0,119 для «сверхзвуковой» оболочек (7-й и 11-й столбцы, Табл. 1). Максимальные значения fmax отличаются еще сильнее: максимальное различие значений fmax , связанное с учетом пластичности, составило 10,714 для «звуковой» и 29,03 для «сверхзвуковой» оболочек (8-й и 12-й столбцы, Табл. 3). Рост же различий максимальных значений fmax , вызванных особенностями аппроксимации в гидродинамическом приближении, составляет 4,409 для «звуковой» и 21,02 — для «сверхзвуковой» оболочек, соответственно (8-й и 12-й столбцы, Табл. 1). Таким образом, различия максимальных значений fmax , обусловленные учетом физического процесса — пластичности, оказались сравнимыми с максимальными различиями fmax , определяемыми погрешностью конечноразностной аппроксимации.

Третья серия расчетов оболочки выполнена на базе той же модели, что и вторая серия, но отличается значениями параметров девиатора тензора напряжений. Здесь принято: безразмерный модуль сдвига G = 0,68852; коэффициент Пуассона v = 0,282 ; предел текучести Y = 0,004.

Сравнение результатов, полученных во 2-й и 3-й сериях расчетов, даёт представление о влиянии на них параметров модели идеальной пластичности. Из таблицы 4 видно, что снижение предела текучести Y в 1,5 раза (с 0,006 до 0,004) приводит к уменьшению среднего значения удельной тепловой энергии в оболочке примерно в 1,5 раза, то есть поведение тепловой энергии пропорционально поведению Y . Таким образом, с помощью вариации предела текучести в рамках модели идеальной пластичности можно существенно изменить диссипацию энергии и, следовательно, погрешность, порождаемую физической моделью.

• 6.    Заключение

Представленные в таблицах 1–4 результаты численных экспериментов показали, что при моделировании динамических процессов в оболочках алгоритм «ВОЛНА» [12], основанный на методе Куропатенко[10], обеспечивает наиболее высокую точность расчёта величин. Алгоритмы с искусственной вязкостью (типа Неймана–Рихтмайера) приводят к «математической» диссипации энергии даже в тех случаях, когда она должна отсутствовать. Разброс значений при наличии «математической» диссипации энергии сравним с разбросом, найденным с учетом диссипации энергии на пластическом участке деформирования. Таким образом, применение моделей с искусственной вязкостью для математического моделирования динамических процессов в реальных средах не позволяет достоверно определить величину физической диссипации энергии.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проект № 10-01-00032).