О моделировании пястно-запястного сустава большого пальца руки

Большой палец руки играет ключевую роль в нормальном функционировании всей кисти. Наиболее сложным и в то же время наиболее важным для обеспечения «нормального» движения всего пальца является пястно-запястный сустав. Этот сустав (рис. 1) образован двумя костями и является разновидностью двухосных суставов – седловидным суставом. Он образован дистальной суставной поверхностью кости-трапеции и проксимальной суставной поверхностью первой пястной кости. Необходимо отметить, что геометрия пястно-запястного сустава значительно варьируется у разных индивидуумов.

Клиническая практика показывает, что этот сустав часто страдает от артрита [5]. Поэтому исследование свойств данного сустава с прицелом на разработку эффективных протезов является весьма актуальным.

С этим связано наличие обширной литературы – как медицинской, так и биомеханической, посвященной экспериментальному и теоретическому исследованию пястно-запястного сустава и, в частности, кинематики этого сустава. Так, в статьях [3, 4] описаны эксперименты in vitro , в которых регистрировались пространственные координаты наборов точек большого пальца при разных его положениях относительно кисти. На базе этой информации определялось направление осей вращения (сгибание/разгибание и приведение/отведение) в суставах большого пальца. Показано, что эти оси можно считать фиксированными по отношению к костям пальца. Следует отметить, что во всех работах зафиксирован весьма широкий диапазон изменения параметров рабочего пространства большого пальца у разных людей. В статьях [1, 6, 7] описаны механические модели большого пальца, представляющие собой кинематическую цепь, которая состоит из нескольких жестких стержней, соединенных цилиндрическими шарнирами. В них считается целесообразным с точки зрения повышения точности описания кинематики пальца и усилия на его кончике моделировать пястно-запястный сустав с помощью двух цилиндрических шарниров, оси которых не перпендикулярны и не пересекаются.

Однако задача построения адекватной модели пястно-запястного сустава еще далека от разрешения. Для этого представляется необходимым разработать такую модель, которая бы достаточно точно описывала область движений пальца, регистрируемую в экспериментах, и в то же время включала как можно меньше степеней свободы и параметров, подлежащих идентификации по результатам экспериментов.

Рис. 1. Положение пястно-запястного сустава в кисти руки

В настоящей работе описаны исследования, проведенные совместной российско-тайваньской группой ученых из Национального университета Чен Кун ( NCKU , Тайнань) и НИИ механики МГУ имени М.В. Ломоносова. В NCKU проведены две серии экспериментов по регистрации положения костей, образующих пястнозапястный сустав. Была разработана методика определения характерных точек на этих костях и формирования систем координат, связанных с этими костями. В НИИ механики МГУ имени М.В. Ломоносова построена математическая модель сустава и проведена попытка ее верификации на основе полученных экспериментальных данных. Показано, что использование предлагаемой в литературе модели с двумя степенями свободы не обеспечивает достаточно точного описания относительных положений костей. В связи с этим в модель введены две дополнительные степени свободы, соответствующие «проскальзыванию» костей друг относительно друга. Была создана оригинальная методика и построен алгоритм идентификации параметров модели. Определены значения параметров, которые позволили достичь достаточно хорошего согласования с экспериментальными данными.

Экспериментальные исследования

Для изучения взаимного положения костей, образующих пястно-запястный сустав, на факультете биомедицины NCKU были проведены две серии экспериментов in vitro . В каждой из этих серий использовался свой образец руки. Рука при этом закреплялась в фиксаторе, а к сухожилиям мышц большого пальца с помощью специального устройства прикладывалась сила.

В экспериментах первой серии некоторая фиксированная сила прикладывалась по очереди к одному из сухожилий мышц большого пальца. Были задействованы сухожилия следующих мышц: flexor pollicis longus ( FPL ), extensor pollicis longus ( EPL ), abductor pollicis longus ( APL ), abductor pollicis brevis ( APB ), adductor pollicis ( ADD ) (в указанном порядке). Величины прикладываемой силы составляли 0; 0,2; 0,5; 0,7 кгс (для ADD нагрузку в 0,7 кгс реализовать не удалось из-за технических ограничений). Таким образом, всего было исследовано 19 различных положений большого пальца.

В экспериментах второй серии (рис. 2), в отличие от предыдущих, сила прикладывалась одновременно к нескольким сухожилиям указанных мышц большого пальца таким образом, чтобы кончик большого пальца находился в одном из четырех заданных положений (в основании одного из других пальцев руки) и на нем развивалось заданное усилие (измеряемое с помощью датчика нагрузки). Всего было проведено

Рис. 2. Экспериментальный стенд

12 экспериментов: большой палец в «нейтральном» положении (нагрузка к сухожилиям не приложена), кончик большого пальца прижат к основанию указательного пальца (усилие на кончике 0; 0,2; 0,4 кгс), кончик большого пальца прижат к основанию среднего пальца (усилие на кончике 0; 0,2; 0,4 кгс), кончик большого пальца прижат к основанию безымянного пальца (усилие на кончике 0; 0,2; 0,4 кгс), кончик большого пальца прижат к основанию мизинца (усилие на кончике 0; 0,2 кгс).

В ходе экспериментов с помощью компьютерной томографии регистрировались положения первой пястной кости и кости-трапеции, после чего на базе полученных данных рассчитывались положения характерных точек на этих костях. Затем по этим точкам в соответствии методикой, описанной в статье [2], определялись координаты центра О M основания первой пястной кости и углы, задающие ориентацию осей системы координат O M X M Y M Z M , связанной с первой пястной костью, относительно неподвижной системы координат O T X T Y T Z T , связанной с костью-трапецией.

Модель с двумя степенями свободы

Сначала была предпринята попытка воспользоваться известным из литературы подходом и, как было описано выше, ограничиться двумя цилиндрическими шарнирами со скрещивающимися и неперпендикулярными осями (рис. 3). Первый из этих шарниров жестко связан с костью-трапецией и моделирует сгибание/разгибание ( F–E ). Второй жестко связан с первой пястной костью и моделирует приведение/отведение ( A–A ).

В рамках этого подхода имеют место следующие соотношения:

e Mx  ^MAA ^{( ф} 2 ) M FE ( Ф 1^{) е} Tx ,   e My   M AA ( Ф 2 ) M FE ^{( ф} 1^{) е} Ty ,   e Mz   M AA ( Ф 2 ) M FE ( Ф 1 ) ^е Tz ,

O T O M = O T O 1 + M fe ( Ф 1 ) Г 1 + M aa ( Ф 2 ) M fe ( Ф 1К

Здесь e _{Mx , y , z} и e _{Tx , y , z} – орты осей координат, связанных с первой пястной костью и с трапецией соответственно; ф ₁₂ - углы поворота вокруг осей первого и второго шарнира; M_fe ( Ф 1 ) и М_AA ( ф ₂) - соответствующие матрицы поворота; O T O 1 , г ₁₂ -некоторые постоянные векторы.

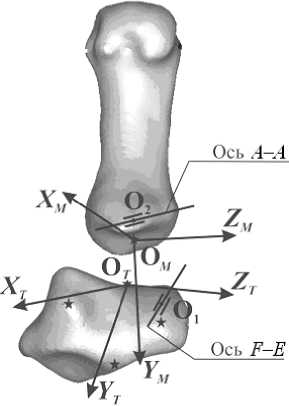
Рис. 3. Модель пястно-запястного сустава, содержащая два шарнира со скрещивающимися и неперпендикулярными осями

Таким образом, модель содержит десять параметров: четыре параметра, определяющие направления осей первого и второго шарниров, три компоненты вектора O _T O ₁ и три компонента вектора r ₁ . Отметим, что эти параметры являются индивидуальными и могут различаться (вообще говоря, достаточно сильно) для разных людей. Соответственно, они различны для экспериментов первой и второй серий. В то же время углы поворота необходимо подбирать для каждого положения отдельно – так, чтобы обеспечить минимальное рассогласование между расчетными и экспериментально зарегистрированными положениями первой пястной кости.

Отметим, что задачу идентификации параметров можно решать в два этапа: сначала определить направления осей шарниров и углы поворота вокруг этих осей, а уже затем найти векторы O _T O ₁ , r ₁ и r ₂ . При этом r ₂ при заданных прочих параметрах определяется однозначно по положению, принятому в качестве номинального (в обеих сериях экспериментов в качестве такового использовалось положение пальца до прикладывания нагрузки). Такой подход позволяет существенно уменьшить объем вычислений, которые необходимо произвести в ходе идентификации параметров.

На первом этапе с помощью метода покоординатного спуска были определены направления осей шарниров. При этом для каждого положения углы поворота в шарнирах определялись путем минимизации функционала, равного корню из суммы квадратов углов между расчетными и экспериментальными координатными осями.

Результаты расчетов приведены в табл. 1 и 2 ( α _{x , y , z} – углы между расчетным и измеренным направлением осей O M X M , O M Y M , O M Z M соответственно).

Таблица 1

Ориентация осей для экспериментов серии 1

Мышца	Сила, кгс	α x	α y	α z	Мышца	Сила, кгс	α x	α y	α z
FPL	0	0,8	0,9	0,7	APL	0,5	11,2	7,8	10,0
FPL	0,2	1,1	0,8	1,3	APL	0,7	11,4	7,8	11,3
FPL	0,5	2,2	1,5	2,0	APB	0	1,3	0,9	1,5
FPL	0,7	2,7	2,1	1,7	APB	0,2	1,9	2,0	0,8
EPL	0	0,7	0,8	0,3	APB	0,5	4,0	3,2	2,4
EPL	0,2	2,3	2,4	0,9	APB	0,7	5,7	5,1	2,7
EPL	0,5	9,9	6,5	10,0	ADD	0	1,2	1,4	1,5
EPL	0,7	11,4	7,5	11,3	ADD	0,2	1,5	1,0	1,5
APL	0	1,3	1,4	0,6	ADD	0,5	0,4	0,4	0,3
APL	0,2	11,0	7,9	9,5

Таблица 2

Ориентация осей для экспериментов серии 2

Положение	Усилие, кгс	α x	α y	α z	Положение	Усилие, кгс	α x	α y	α z
Нейтральное	0	0,1	0,1	0,1	2	0,4	1,6	2,1	2,6
1	0	2,7	8,6	8,9	3	0	3,0	3,0	3,9
1	0,2	3,2	3,9	3,6	3	0,2	0,5	0,9	1,0
1	0,4	5,5	7,9	7,3	3	0,4	4,7	6,4	5,9
2	0	5,4	6,6	6,3	4	0	8,0	5,0	7,2
2	0,2	1,0	2,3	2,2	4	0,2	5,1	5,0	6,5

Максимальная невязка по ориентации первой пястной кости составляет 11,4 ° . При этом для 60% положений углы не превышают 4 ° . Такой уровень точности представляется вполне приемлемым. Таким образом, ориентацию первой пястной кости в рамках данного подхода удается описать достаточно хорошо.

Следующим этапом идентификации параметров является определение параметров, отвечающих за описание положения первой пястной кости (т.е. за положение точки O M ).

С помощью метода покоординатного спуска в сочетании с методом наименьших квадратов были определены значения компонентов векторов O _T O ₁ и r ₁ , обеспечивающие наименьшую разницу между расчетным и экспериментальным положениями указанной точки. Результаты приведены в табл. 3 и 4 ( в - угол между расчетным и измеренным направлением вектора O T O M ; A r - относительная невязка по длине O T O M , т.е. разность расчетной и измеренной длин этого вектора, отнесенная к измеренной длине).

Максимальная относительная невязка по длине вектора O T O M составила 55% для первой серии и 44% для второй, а угол между расчетным и измеренным векторами достиг 19 ° для первой серии и 24 ° для второй. Таким образом, данная модель не позволила определить положение точки O M с достаточной точностью.

Таблица 3

Положение точки O M для экспериментов серии 1

Мышца	Сила, кгс	в, град	A r , %	Мышца	Сила, кгс	в, град	A r , %
FPL	0	0,0	0	APL	0,5	5,3	16
FPL	0,2	1,6	5	APL	0,7	0,7	6
FPL	0,5	3,3	13	APB	0	2,8	16
FPL	0,7	3,3	19	APB	0,2	13,9	25
EPL	0	1,1	5	APB	0,5	18,1	33
EPL	0,2	19,1	33	APB	0,7	17,8	42
EPL	0,5	3,5	11	ADD	0	5,2	12
EPL	0,7	3,7	7	ADD	0,2	0,7	9
APL	0	1,1	5	ADD	0,5	1,2	14
APL	0,2	16,5	55

Таблица 4

Положение точки O_M для экспериментов серии 2

Положение	Усилие, кгс	в, град	A r , %	Положение	Усилие, кгс	в, град	A r , %
Нейтральное	0	0	0	2	0,4	11,3	20
1	0	14,6	26	3	0	6,5	13
1	0,2	11,0	22	3	0,2	12,7	25
1	0,4	9,46	20	3	0,4	10,67	19
2	0 кгс	16,1	28	4	0	22,8	42
2	0,2 кгс	11,7	20	4	0,2	24,1	44

Модель с дополнительными степенями свободы

Одним из возможных способов модификации модели является увеличение числа степеней свободы. Были введены две дополнительные степени свободы, соответствующие перемещению центров шарниров вдоль прямых ^ _т и ^_м , жестко связанных соответственно с костью-трапецией и с первой пястной костью (рис. 4).

В рамках предложенной модели формула для расчета положения начала системы координат, связанной с первой пястной костью, приняла следующий вид:

O т O м = O т O1 + Mfe (ф^ + Maa (^2) Mfe (Ф1)г2 + x1e т + x 2 Maa (^2) Mfe (Ф1)e м , где x12 - смещения вдоль осей ^т и ^м; eт, eм - единичные векторы осей ^т и ^м.

Модифицированная модель содержит четырнадцать параметров, которые подлежат идентификации на базе экспериментальных данных: к параметрам, описанным ранее, добавляются четыре параметра, определяющие направления осей ^ _т и ^ _м относительно систем координат, связанных с соответствующими костями (эти параметры также являются индивидуальными и могут отличаться для разных людей). Кроме того, для каждого положения требуется определить соответствующие ему значения координат x ₁ и x ₂ .

Для идентификации дополнительных параметров была проведена серия расчетов (при этом для остальных параметров и углов поворота вокруг осей шарниров были приняты значения, определенные на предыдущем этапе). В ходе этих расчетов с помощью метода покоординатного спуска определялись значения параметров модифицированной модели пястно-запястного сустава, обеспечивающие минимальное отклонение расчетных данных от экспериментальных.

В результате были получены следующие оценочные значения параметров: для серии 1:

efe =(0; 0; 1)T, eaa =(—0,13; 0,36; 0,92)T, eT =( 0,91; 0,39; 0,14) T, e M =( 0,33; -0,71; 0,62) T, r1 =(22,4; 15,6; 5,5)T, r2 =(23,0; -77,6; 20,5)T ;

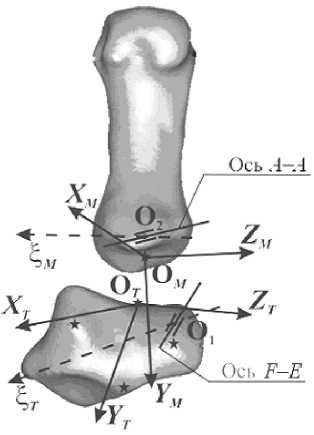
Рис. 4. Уточненная модель пястно-запястного сустава для серии 2:

efe = (-0,15; 0,35; 0,92) T, eaa =(-0,04; 0,58; 0,82) T, eT =( 0,27; 0,76; 0,59) T, em =(-0,15; -0,78; 0,61) T, r1 =( 26,2; -54,5; -72,5) T, r2 =(-1,9; -7,0; -52,2) T, где eFE , eAA – единичные векторы осей шарниров, заданные в системах координат, связанных с костью-трапецией и с первой пястной костью, соответственно; eT ,eM – единичные векторы осей ^T и ^M .

Результаты расчетов приведены в табл. 5 и 6:

Таблица 5

Положение точки O M для экспериментов серии 1 (модифицированная модель)

Мышца	Сила, кгс	Р, град	A r , %	Мышца	Сила, кгс	Р, град	A r , %
FPL	0	0	0	APL	0,5	1,1	3
FPL	0,2	0,9	2	APL	0,7	1,3	4
FPL	0,5	1,2	2	APB	0	2,5	4
FPL	0,7	4,9	9	APB	0,2	0,4	1
EPL	0	0,4	1	APB	0,5	2,5	5
EPL	0,2	3,4	6	APB	0,7	3,4	6
EPL	0,5	2,2	5	ADD	0	3,5	6
EPL	0,7	0,2	1	ADD	0,2	0,1	0
APL	0	1,1	2	ADD	0,5	2,4	4
APL	0,2	3,5	7

Таблица 6

Положение точки O M для экспериментов серии 2 (модифицированная модель)

Положение	Усилие, кгс	Р, град	A r , %	Положение	Усилие, кгс	Р, град	A r , %
Нейтральное	0	0	0	2	0,4	1,3	4
1	0	2,1	4	3	0	0,6	2
1	0,2	2,3	7	3	0,2	0,7	2
1	0,4	2,5	8	3	0,4	2	9
2	0	1,6	5	4	0	0,2	1
2	0,2	1,4	4	4	0,2	0,6	4

Видно, что выбранные значения параметров обеспечивают достаточно хорошее согласование с экспериментальными данными. Так, максимальное значение угла в составляет 4,9 ° , а максимальное значение A r - 9%. При этом для 83% экспериментальных положений пальца р <  3 ° , для 72% положений A r <  5% .

Заключение

Таким образом, использование для описания кинематики пястно-запястного сустава большого пальца руки модифицированной модели, содержащей, помимо вращательных, также и поступательные степени свободы, представляется целесообразным. По-видимому, этот результат коррелирует с данными о наличии «проскальзывания» первой пястной кости относительно кости-трапеции, недавно полученными тайваньской стороной.

Работа выполнена при поддержке Российского фонда фундаментальных исследований (грант № 10-08-92001) и Тайваньского национального совета по науке.