О моделировании подтопления и дренирования земель с помощью фортрана

Фильтрация подземных вод количественно может быть рассчитана с помощью закона Дарси. Необходимо совершенствовать методологию моделирования движения воды в почвах и грунтах, отталкиваясь от изначальных теоретических основ с опорой на опытные данные. Наиболее современный способ моделирования – использование численных методов. Автор отдает предпочтение методу конечных разностей (МКР). Далее показано использование языка программирования фортран для решения поставленных практикой задач моделирования подтопления и дренирования.

Объекты и методы

Компьютерное моделирование водопонижения из 13 скважин выполнено для стадии строительства многофункционального спортивного комплекса «Дворец спорта» в городе Калуге. Научно-исследовательская работа проведена на основании исходных данных, изложенных в техническом отчете об инженерно-геологических изысканиях 11267-ИГИ ОАО «КалугаТИСИЗ» 2014 г. Все необходимые данные предоставил советник генерального директора территориального проектного института ТПИ Омскграж-данпроект, кандидат технических наук Раис Шакирович Абжалимов.

Площадка изысканий расположена в городе Калуге по улице Ленина, на территории существующего стадиона. На момент проведения изысканий площадка занята под футбольное поле, трибуны, административное помещение и торговые павильоны. Рельеф ровный, спланированный. Отметки рельефа 193,00–195,60 м. Перепад – 2,6 м. Климат умеренно континентальный. Инженерно-гидрогеологические данные схематизированы по рекомендациям справочного пособия к СНиП [1]. За условный (относительный) ноль принята средняя отметка низа водонасыщенного песка с абсолютной отметкой 180,25 м. Коэффициент фильтрации песка k = 2 м/сут. Его средняя мощность M = 6 м. Выше песка до поверхности земли расположен суглинистый грунт толщиной 7 м с коэффициентом фильтрации ничтожно малой величины 0,00003 м/сут. Уровень подземных вод (УПВ) залегает на 2 м ниже уровня земли. Водонасыщенный песок подстилается водоупорными глинистыми грунтами.

Средняя глубина водопонизительной скважины принята 20 м. Она проходит с поверхности земли 7 м суглинистого грунта, ниже – 6 м водонасыщенного песка и заглубляется на 5 м в водоупорные глинистые грунты. Общая глубина скважины около 20 м, в том числе 2 м отстойник. Напор в скважине при водопонижении принят постоянным на отметке 180,25 м. В схематизированной схеме водоносного пласта это соответствует низу песка при контакте с водоупором. Скважина гидродинамически совершенная, ее фильтр принят на всю мощность М = 6 м водонасыщенного песка.

Компьютерная модель построена методом конечных разностей (МКР). Рассмотрена напорная нестационарная фильтрация подземной воды в песке при откачке из 13 скважин по схеме неограниченного в плане водоносного пласта. Напор в скважине Нс = 0 м. Начальный естественный напор в подземных водах Не = 13 м. Мощность во- доносного песчаного пласта М = 6 м. Коэффициент фильтрации песка, по данным изысканий, k = 2 м/сут. Коэффициент водоотдачи песка принят по Бецинскому [2]

ц = 0 ,117 7 k = 0 , 117^2 = 0 , 13 . (1)

Для моделирования принят участок размером в плане 500 на 500 метров.

Схема расположения водопонизительных скважин, предложенная Р.Ш. Абжали-мовым, показана на рис. 1. На расстоянии около 15 м от скважин 1-го и 5-го верхнего ряда расположены, соответственно, два 5-этажных жилых дома (5КЖ) – левый и правый. Для них на компьютерной модели необходимо было получить информацию о понижении УПВ при водопонижении.

Первая контрольная точка 1КТ по определению пониженного уровня подземных вод (УПВ) находится в центре котлована здания бассейна (рис. 1). Вторая контрольная точка 2КТ – в центре котлована здания дворца.

Компьютерная модель водопонижения методом конечных разностей (МКР) использует явную схему: подробности изложены в нашей монографии «Фильтрационные расчеты и компьютерное моделирование при защите подтопления в городском строительстве» (Омск, СибАДИ, 2002).

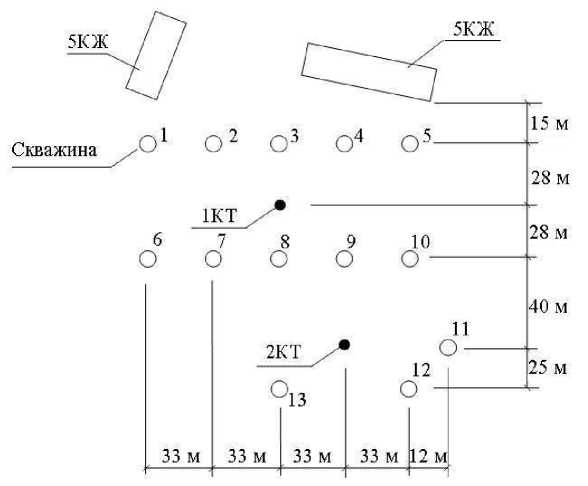
Рис. 1. Схема расположения водопонизительных скважин

Радиус водопонизительной скважины принят R с = 0,1 м. Шаги пространственной МКР-сетки по оси х (по горизонтали) и оси у (по вертикали) приняты равными, соответственно, dx = dy = dL = 0,5 м. Это связано с тем, что при задании постоянного напора в скважине на уровне низа водонасыщенного песка Н с = 0 м (относительная отметка) R c и dL связаны соотношением вида

R c = 0,2 ∙ dL = 0,2 ∙ 0,5 = 0,1 м.                            (2)

Шаг времени на модели dt принят максимально возможный с учетом критерия устойчивости счета МКР-модели по явной схеме и вычислен:

, ц - dL    0 , 13 • 0 , 5

dt =-------=---------= 0 , 000677 сут = 58,5 сек ~ 1 мин.

4 • к • M 4 • 2 • 6

При размерах участка моделирования в плане 500 х 500 м при пространственном шаге dx = dy = dL = 0,5 м получается плановая модель фильтрации подземных вод к 13 водопонизительным скважинам, работающим в режиме постоянной откачки с фильтрационным напором Н с = 0 м. Количество узлов модели превышает миллион, так как 1001 ∙ 1001 = 1 002 001.

Заметим, что известная компьютерная программа геологической службы США ModFlow PMwin, версия 5.3 которой официально сертифицирована для применения в России, способна применять МКР-модели с максимальным количеством узлов не более 250 тыс. Это для целей нашего моделирования водопонижения с количеством узлов более 1 млн непригодно.

Поэтому в плане инновации решено построить МКР-модель водопонижения с оригинальной разработкой на языке программирования Fortran 95 [3]. С целью независимости от иностранных технологий (импортозамещение) использовано свободное программное обеспечение с 64-битной операционной системой Linux. Компилятор фортрана gfortran. Исходный код программы записан в файле Bass13cKB.f95 и скомпилирован в исполняемый файл Bass13cKB командой gfortran–std=f95 Bass13cKB.f95 Bass13cKB

Время водопонижения на модели рассчитано с такими значениями (с учетом организации строительства):

0,1 сут; 1 сут; 5 сут; 10 сут; 15 сут; 30 сут; 45 сут; 60 сут.

Время расчета модели на компьютере с тактовой частотой 2,13 GHz получалось от нескольких секунд до 10 мин. Результаты расчета записаны в выходные текстовые файлы. По ним построены карты напоров подземных вод при работе системы из 13 водопонизительных скважин, что выборочно показано на рис. 2–4.

1-е сутки

Не = 13 м, Нскв = 0 м, М = 6 м, Rскв = 0,1 м

K = 2 м/сут, mu = 0,13, t = 1 сут, 500х500 м2, шаг сетки 0,5 м 13 скважин (рис. 1)

Понижение УПВ = 0,139 м (контр. точка 1КТ)

Понижение УПВ = 0,012 м (контр. точка 2КТ) Понижение УПВ под левым 5КЖ = 0,157 м

Понижение УПВ под правым 5КЖ = 0,670 м

Рис. 2. Прогнозная карта водопонижения на 1-е сутки

5-е сутки

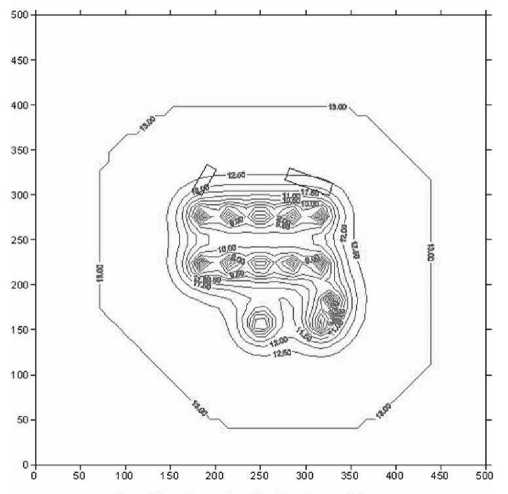
Не = 13 м, Нскв = 0 м, М = 6 м, Rскв = 0,1 м

K = 2 м/сут, mu = 0,13, t = 5 сут, 500х500 м2, шаг сетки 0,5 м

13 скважин (рис. 1)

Понижение УПВ = 2,746 м (контр. точка 1КТ)

Понижение УПВ = 1,495 м (контр. точка 2КТ)

Понижение УПВ под левым 5КЖ = 1,303 м

Понижение УПВ под правым 5КЖ = 2,423 м

Рис. 3. Прогнозная карта водопонижения на 5-е сутки

30-е сутки

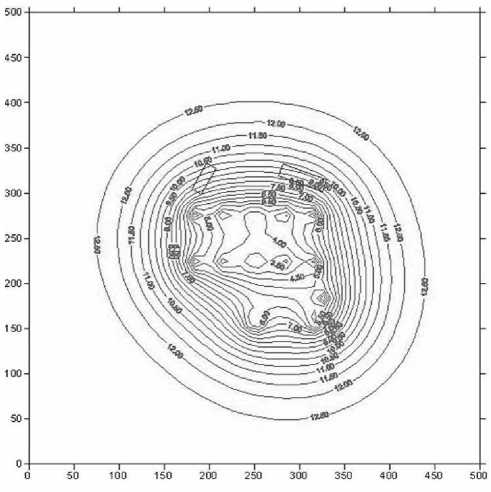
Не = 13 м, Нскв = 0 м, М = 6 м, Rскв = 0,1 м

K = 2 м/сут, mu = 0,13, t = 30 сут, 500х500 м2, шаг сетки 0,5 м

13 скважин (рис. 1)

Понижение УПВ = 9,056 м (контр. точка 1КТ)

Понижение УПВ = 7,366 м (контр. точка 2КТ)

Понижение УПВ под левым 5КЖ = 4,439 м

Понижение УПВ под правым 5КЖ = 5,934 м

Рис. 4. Прогнозная карта водопонижения на 30-е сутки

Водопритоки в скважины в течение водопонижения сведены в таблицу по временным периодам. С течением времени водопонижения водопритоки в скважины уменьшаются. Понижение уровня подземных вод (УПВ) увеличивается. Разумеется, при условии постоянной откачки воды из скважин, которая должна быть автоматизирована. Уровень воды в скважинах рекомендовано поддерживать постоянным на уровне низа водонасыщенного песка. Фильтры скважин расположить в пределах водонасыщенного слоя грунта, то есть скважины должны быть гидродинамически совершенными.

Прогнозные притоки подземных вод в скважины 1–13 (рис. 1), м3/сут

№ скв.	Время от начала откачки при водопонижении, сут
	0,1	1	5	10	15	30	45	60
1	104,0	63,0	41,4	30,7	24,6	16,0	12,4	10,4
2	104,0	62,7	36,8	24,0	17,5	9,6	6,9	5,6
3	104,0	62,7	36,5	23,0	16,1	8,2	5,7	4,5
4	104,0	62,7	36,8	23,9	17,3	9,2	6,5	5,2
5	104,0	63,0	41,3	30,5	24,2	15,0	11,3	9,3
6	104,0	63,0	41,3	30,5	24,1	14,9	11,2	9,2
7	104,0	62,7	36,6	23,3	16,2	8,0	5,4	4,2
8	104,0	62,7	36,1	21,6	14,0	5,9	3,7	2,8
9	104,0	62,7	36,0	21,4	14,0	6,0	3,8	2,9
10	104,0	62,9	38,7	25,6	18,5	9,8	6,8	5,4
11	104,0	62,4	38,1	27,4	21,5	13,2	9,8	8,1
12	104,0	62,4	40,3	30,5	24,8	16,1	12,3	10,2
13	104,0	63,3	46,1	36,4	29,4	18,1	13,2	10,7

Анализируя прогнозные карты водопонижения (рис. 2–4), нетрудно обнаружить: с течением времени работы скважин, из которых непрерывно ведется откачка, воронки кривых депрессий пониженного УПВ начинают сливаться в общую воронку водопонижения. Это особенно заметно на 30-е сут работы водопонизительной системы (рис. 4). То есть подтверждается гипотеза «большого колодца», принятая для системы близко расположенных скважин [4]. Водопритоки скважин (таблица) в начале водонижения практически одинаковые, скважины вначале не влияют друг на друга. Затем, в ходе непрерывной откачки воды, скважины начинают влиять все больше и больше, причем у внутренних скважин типа 8 и 9 (рис. 1) водоприток уменьшается в десятки раз.

Рассмотрим более подробно приемы программирования и алгоритмы, примененные в ходе данной научно-исследовательской работы.

В самом начале кода программы было применено новое замечательное ключевое слово фортрана allocatable [5–7] для объявления массива напоров, а именно:

real, allocatable :: H0(:,:) real, allocatable :: H(:,:)

где Н0 – начальные напоры непониженного УПВ; Н – напоры УПВ при водопонижении.

Это позволило записывать программный код компактно, без применения громоздких циклов, как, например, обычно принято в ФОРТРАН 77.

МКР-схема была принята явная, для нестационарной фильтрации подземных вод. В терминах вычислительной математики мы применили явную разностную схему для решения дифференциальных уравнений фильтрации параболического типа, то есть для нестационарного движения подземных вод в плане в рамках гипотезы Буссинеска.

В отличие от традиционного алгоритма вычислительной математики с циклом for-end [8, с. 185], для решения упомянутой разностной схемы применен вложенный цикл фортрана do-end. Суть данного приема в том, что параметр времени моделирования вынесен из тела массива. Этот особый алгоритмический прием позволил избавиться от ограничения памяти персонального компьютера (ПК), т.е. фактически предохраниться от overflow-переполнения оперативной памяти ПК. В результате алгоритм стал быстрым. Тесты показали увеличение скорости расчета модели на три порядка, т.е. примерно в тысячу раз.

Заключение

В представленной работе предпринято исследование по совершенствованию методологии моделирования движения подземных вод. Показано, что с помощью фортрана с учетом особых алгоритмов можно существенно ускорить расчет компьютерных моделей водопонижения при защите от подтопления земель. Это должно повысить надежность проектирования защиты от подтопления в городском строительстве и сельском хозяйстве.

V.I. Sologaev

Omsk State Agrarian University named after P.A. Stolypin, Omsk

About the modeling of underflooding and land drainage with the fortran