О модификации процесса маршрутизации в вычислительных сетях с помощью нечеткой логики

В статье исследованы вопросы маршрутизации в сети. Наглядно демонстрируются все преимуще-в IP-сетях. Авторы разрабатывают алгоритмы на ства созданного алгоритма.

основе нечетких множеств. Моделируется сеть для исследования данного алгоритма. С помощью него        Ключевые слова: моделирование сети, опти- находится оптимальный маршрут передачи данных мальный маршрут, нечеткая логика, система типа

Сугэно, терм множества, комбинация термов, синтезированная нечеткая система

Компьютерные сети стали неотъемлемой частью нашей жизни. Все мы пользуемся электронной почтой, Web-ресурсами, сетью Internet. Вопрос маршрутизации является основополагающим в этом процессе. Поэтому последнее время этому вопросу уделяется все больше внимания. Ведь от выбора маршрута будет зависеть, получите вы свое сообщение или нет. Задачу выбора маршрута решают маршрутизаторы, а также конечные узлы. Маршрут выбирается на основании имеющейся у этих устройств информации о текущей конфигурации сети и критерия выбора маршрута. При оценке сетей с коммутацией пакетов рассматриваются следующие основные количественные характеристики: задержка, скорость передачи, стоимость, надежность и количество пройденных в маршруте промежуточных маршрутизаторов. Все известные алгоритмы маршрутизации можно свести к трем:

• -    подход на основе маршрутизации по вектору расстояния, в соответствии с которым определяются направление (вектор) и расстояние до каждого канала в сети;

• -    подход на основе оценки состояния канала (также называемый выбором наикратчайшего пути), при котором воссоздается точная топология всей сети (или, по крайней мере, той части, где размещается маршрутизатор);

• -    гибридный подход, объединяющий аспекты алгоритмов с определением вектора расстояния и оценки состояния канала [2].

Полученная в результате анализа информация о маршрутах следования пакетов помещается в таблицу маршрутизации. Таблица маршрутизации имеет четыре основных поля: адрес назначения, сетевой адрес следующего маршрутизатора, сетевой адрес выходного порта, расстояние до сети назначения. Процедура выбора маршрута, в свою очередь, включает в себя две задачи: определение маршрута и оповещение сети о выбранном маршруте. Так как в таблице чаще всего указывается не весь IP-адрес, а только номер сети назначения, для всех пакетов, направляемых в одну и ту же сеть, будет предлагаться один и тот же маршрут. Можно создать специфический маршрут, но когда речь идет о большом объеме информации, это не совсем целесообразно [3].

Итак, необходим некий алгоритм маршрутизации пакетов, учитывающий следующие параметры: приоритет сообщений, возможность использования определенных каналов, перегрузку сети, время прохождения пакета. Для этого рассмотрим процесс маршрутизации пакета данных с помощью модели составной вычислительной сети, представляющей собой полный граф из пяти вершин (см. рис. 1).

Рис. 1. Граф вычислительной сети

Проанализировав модель сети, приходим к выводу, что маршрут должен быть проложен с учетом пропускной способности и количества переходов. Это маршрут (см. рис. 1) 1-5, пропускная способность его 1,544 Мбит/С, количество переходов минимальное. Но если все пакеты будут передаваться по этому маршруту, произойдет сбой работы в сети. Поэтому выбираются несколько маршрутов в зависимости от загруженности сети. Такие записи записываются в таблицу маршрутизации, тем самым маршрутизатор реализует режим баланса загрузки маршрутов, отправляя пакеты попеременно по каждому из маршрутов. Однако сложно определить, какой из данных маршрутов предпочтителен для той или иной информации. С помощью таблицы маршрутизации процесс перенаправления пакетов в зависимости от многих компонентов не учитывается. Сама таблица маршрутизации постоянно требует обновления, что приводит подчас к сбою в работе сети.

Предлагается для определения оптимального маршрута разработать алгоритм на основе нечетких множеств. Нечеткая логика позволяет создать динамическую модель с необходимой степенью точности. С помощью созданного алгоритма мы сможем оптимизировать скорость передачи пакетов, уменьшить потерю пакетов, распределить информационные потоки в зависимости от их важности, оперативно реагировать при возникновении внештатных ситуаций. Чтобы исследовать работу этого алгоритма разработаем модель составной вычислительной сети (см. рис. 2). Сеть будет состоять из пяти переходов, пропускная способность которых разная. На одном отрезке сети скорость передачи информации 10 Мбит/С, на другом – 100 Мбит/С. Наша задача – найти оптимальный маршрут для передачи сооб- щений с разной степенью важности. Для этого исследуем работу сети и выделим наиболее значимые этапы. Это количество переходов (k), пропускная способность сети (t), время прохождения пакетов (g), важность передаваемого сообщения (v).

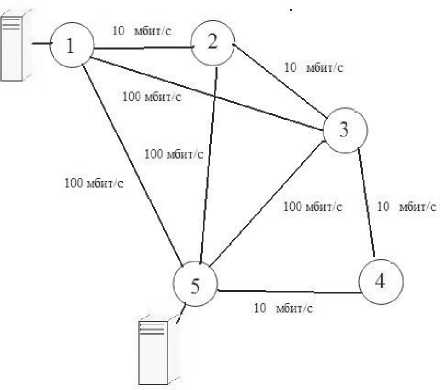
Рис. 2. Сеть с указанием пропускной способности

Разработаем правила, которые задают связь входных переменных с выходными с помощью нечетких параметров. Для лингвистической оценки входных и выходных переменных введем следующие терм-множества:

• -    х1 – важные сообщения (VV – 100%), средней важности сообщения (СV – 70%), маловажные сообщения (МV – 50%);

• -    х2 – скорость передачи информации по сети максимальная (Т = 100 мбит/С), скорость передачи информации по сети средняя (ТС), минимальная скорость передачи информации (МТ = 10 мбит/С);

• -    х3 – максимальное время прохождения пакета (G=30 С), среднее время прохождения пакета (GC), минимальное время прохождения пакета (MG=10 С);

• -    у – максимальное количество переходов (K = 4); среднее количество переходов (КС); минимальное количество переходов (МК = 1).

Эти термы определены в таблице 1.

Таблица 1. База знаний

№	xl	х2	хЗ	У
1	VV	т	MG	мк
2	CV	т	MG	мк
3	CV	тс	GC	КС
4	MV	тс	GC	КС
5	MV	мт	G	к

Как видно из таблицы 1, даже минимальный перебор факторов зависимости передачи протокола по сети приводит к большим расчетам. Чтобы избежать этих расчетов, применим систему типа Сугэно[3]. Модель Сугэно использует правила нечеткой логики следующего вида:

если условие l_i и условие 2_i, то у = bO_i + bl_i*xl + ... +bn_i*xn.

Если значение выходной переменной в правиле задано нечетким множеством, тогда правило может быть представлено нечетким отн о шением. Для нечеткого правила «Если x есть А, то y есть В », нечеткое отношение R задается на декартовом произведении U_x^х и_у, где U-M) – универсальное множество входной (выходной) переменной [3]. Для расчета нечеткого отношения можно применять нечеткую импликацию и t-норму. При использовании в качестве t-нормы операции нахождения минимума расчет нечеткого отношения R осуществляется как

//_й (.г, у) = min («_х (х\р_% (у)), (х, у) е U_х х U _у.

Пусть важность сообщения составляет 100 %. Тогда его доставка должна пройти с минимальным количеством переходов, скорость передачи должна быть максимальной и время в пути минимальное. Смоделируем зависимость параметров сети друг от друга. Входными параметрами будем считать х1 – важность сообщения (VV, CV, MV), х2 – скорость передачи информации по сети (Т,ТС,МТ), х3 –время прохождения пакета (G, GC, MG), а выходной переменной у – количество переходов (MK, КС, К). Полученная зависимость выглядит следующим образом:

• 1.    Если xl= VV, и х2=Т, и хЗ = MG, то у = 1;

• 2.    Если xl— CV, и х2= Т, и хЗ = MG, то у = 1;

• 3.    Если xl= CV, и х2=ТС, и хЗ = GC, то у = 2;

• 4.    Если xl— MV, и х2=ТС, и хЗ = GC, то у = 2;

• 5.    Если xl= MV, и х2=МТ, и хЗ = G, то у = 4.

Применим эти правила на основных этапах проектирования систем типа Сугэно на примере создания системы нечеткого логического вывода, моделирующей зависимость.

Проектирование системы нечеткого логического вывода типа Сугэно состоит в выполнении следующей последовательности шагов. Сначала вводим три входные переменные х1, х2, х3 и одну выходную у. Обозначим термы и введем диапазон изменения переменных согласно выведенным правилам. Каждому терму будут соответствовать три переменные. Тип функции возьмем gaussmf

(яы = ^{е 11} – симметричная гауссовская функция принадлежности) [2]. Число точек дискретизации для построения функции принадлежности примем равным 181.

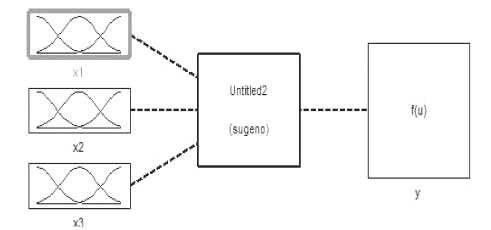
Рис. 3. Модель системы Сугэно

На следующем этапе прописываются правила (соответствующие комбинации термов), которые необходимы для нахождения необходимого маршрута передачи данных. Результат моделирования отображается в графическом окне. Входной вектор в каждом из этих вариантов определения исходных данных задается набором вертикальных линий (см. рис. 4), откуда видно, что построенная модель прохождения пакетов позволяет сделать выбор маршрута быстро без лишних расчетов. При этом учитывается необходимая стратегия маршрутизации.

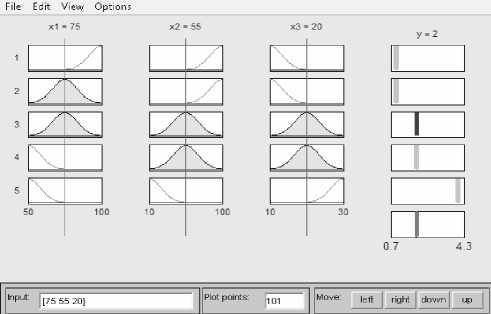
Рис. 4. Отображение результата нечеткого вывода

В зависимости от поставленной задачи задаются те переменные, которые в данный момент являются приоритетными.

Например, в нашем случае, как видно на рис. 4, входной вектор состоит из трех переменных: важность сообщения х1 = 75%, скорость передачи пакета в среднем составит х2 = 55 мбит/С, время прохождения пакета х3 = 20 С, рекомендуемое количество переходов у = 2. Система сама выбрала оптимальный маршрут.

В ОКТИ MATLAB имеется встроенный пакет расширения fuzzy, в котором имеется компонент моделирования системы Сугэно в виде поверхностей входов и выходов.

На рис. 5 показана поверхность «входы и выходы» синтезированной нечеткой системы. Меню X (input), Y (input), Z (output) позволяют поставить в соответствие осям координат входные и выходные переменные. В зависимости от того, какие входные переменные являются необходимыми в данной ситуации, мы можем менять их.

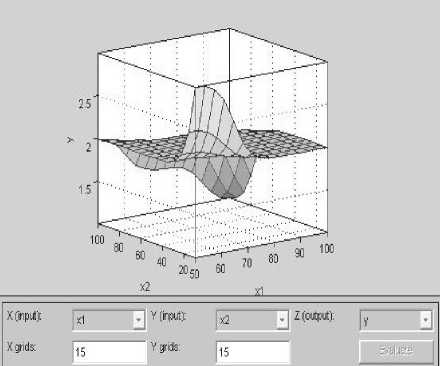
Рис. 5 Поверхность «входы и выходы» для системы Сугэно, определяющая выбор маршрута в сети в зависимости от входных параметров

На рис. 5 показана зависимость у (количество переходов) от х1 (важность сообщения) и х2 (скорость передачи информации). Значения у соответственно меняются в зависимости от задаваемых входных переменных. Изображение поверхности подтверждает, что если важность информации 100%, скорость передачи 100 мбит/С, то и количество переходов будет равно 1. Данное средство просмотра правил вывода позволяет наглядно отобразить сам процесс и быстро получить результат поиска, не применяя сложных расчетов.

Выводы

Из проделанных исследований можно сделать вывод, что использование алгоритма с использованием нечеткой логики эффективно при определении оптимального маршрута. Это позволит адаптировать аппаратуру к конкретным условиям передачи данных и приведет к более оперативному и правильному принятию решений. Нечеткие правила достаточно хорошо описывают сложную нелинейную зависимость. Позволяют применять различные входные данные, оперируя их качест- венными характеристиками и оценками сравнения. При этом модель типа Сугэно наиболее точная. Недостаток этой модели в том, что не всегда ясно, какие линейные зависимости «входы-вы-ход» необходимо использовать. Использование разработанного алгоритма с применением нечеткой логики в решении вопроса маршрутизации обеспечивает преимущества:

• -    можно оперировать нечеткими входными данными: например, важность сообщения, время прохождения сообщения и т.д.;

• -    дает возможность нечеткой формализации критериев оценки и сравнения;

• -    предусматривает при проведении качественных оценок как входных данных, так и выходных результатов;

• -    оперировать степенью достоверности данных их распределением;

• -    проведение быстрого моделирования заданных систем;

• -    точное проведение сравнительного анализа с заданной точностью для построения систем.