О наилучшем полиномиальном приближении функций в весовом пространстве Бергмана
Автор: Лангаршоев Мухтор Рамазонович
Журнал: Владикавказский математический журнал @vmj-ru
Статья в выпуске: 1 т.21, 2019 года.
Бесплатный доступ
Задача нахождения точной оценки величины наилучшего приближения En-1(f)p, 1≤p≤∞, через усредненную величину модуля непрерывности и модуля гладкости самой функции и ее соответствующих производных является одной из интересных задач теории приближений. В свое время Н. П. Корнейчук рассмотрел эту задачу для класса 2π-периодических функций f(x) с выпуклым модулем непрерывности ω(f′,t) в метрике пространства непрерывных функций C[0,2π]. Аналогичную задачу без предположения выпуклости модуля непрерывности граничных значений аналитических в круге функций в пространстве Харди Hp, 1≤p≤∞, рассмотрел Л. В. Тайков. Продолжая исследование указанных авторов, в пространствах Харди Hp, p≥1, М. Ш. Шабозов и М. М. Миркалонова доказали новые точные неравенства, в которых наилучшее полиномиальное приближение аналитических функций оценивается через суммы усредненных значений модулей непрерывности самой функции и некоторой ее производной. В настоящей работе получены точные неравенства между наилучшими полиномиальными приближениями аналитических в единичном круге функций алгебраическими комплексными полиномами и модулями непрерывности и гладкости самой функции и ее второй производной в весовом пространстве Бергмана...
Наилучшее приближение, модуль непрерывности, модуль гладкости, полином, n-поперечник
Короткий адрес: https://sciup.org/143168787
IDR: 143168787 | УДК: 517.5 | DOI: 10.23671/VNC.2019.1.27732
Текст научной статьи О наилучшем полиномиальном приближении функций в весовом пространстве Бергмана
В настоящее время достигнут значительный прогресс в решении задач нахождения точных значений наилучших полиномиальных приближений аналитических в единичном круге функций и вычисления точных значений n-поперечников классов аналитических функций в различных функциональных пространствах (см., например, [1-12] и приведенную там литературу). Представленные в настоящей работе результаты продолжают и развивают исследования в указанном направлении.
Пусть C — множество комплексных чисел. N — множество натуральных чисел ii Z+ — множество целых положительных чисел.
Известно, что аналитическая в единичном круге U = {z G C : |z| < 1} функция
∞ f (z) = ^ Ckzk, z = pe^, 0 С p< 1, k=0
принадлежит весовому пространству Бергмана Bq,Y, 1 С q С го, с конечной нормой [8]
l f ^ Bq’Y = (2П // Y(|z|)|f(z)|q da) < го, 1С q С го,
(U)
где y (|z|) — положительная интегрируемая весовая функция, da — элемент площади, и интеграл понимается в смысле Лебега.
Очевидно, что норму (1) можно записать в виде llf IlBq.Y = ^ 2П j JГ pY(p)|f (peit)|q dpdt\ < ”.
Через f^z) = дтf(pe’'t')/dt'r обозначим производную r-го порядка функции f(z) = f (pci1) по аргумепту t. При этом f‘(z) = f'(z) • zi, f^(z) = {fy-1)(z)};, r > 2.
Величины
"(/IM в
q,γ
= sup ^f«(. + h) - /Д»^ |h|Сt
q,γ,
"2 (СД, 2У в = sup ^f "(fH) в. q,γ и "2 (far), 2t^ в обладают всеми свойствами модуля непрерывности и мо- дуля гладкости (см., например, [13]). Для любых п Е N 11 ak G C, k = 0,1,..., n, символом Pn = Pn(z) : Pn(z) = akzk k=0 обозначим множество алгебраических комплексных полиномов степени не выше п. Величину En(f )Bq,Y =inf {|f — Pn-1|Bq,Y : Pn-1(z) G Pn-1} назовем наилучшим приблимсением функции f (z) G Bq,Y, 1 С q С го, множеством Pn-1. Через Bq,Y,R (1 С q С го, 0 < R С 1) обозначим пространство Бергмана Bq,Y аналитических в круге |z| С R функций f (z), для которых If (-)lBq,Y,R = If(R-)lBq,Y< го, 1 С q С го, 0 В работе [11] доказано, что для произвольной функции f (z) G Bq,Y,R, 1 C q C то, 0 < R C 1, У которой производная fr^z) G Bq,Y, 1 C q C то, при любых r, n G N имеют место точные неравенства En(f)b,,„, C ГпЛ/)^' <2> π/n n En(f)„,..,.„ C ^ J fpB,^dt. № В настоящей работе, исходя из неравенства (2) и (3), мы получим точные оценки величины наилучшего приближения функции f(z) G Bq,Y, 1 C q C то, через усредненные значения модуля непрерывности и модуля гладкости самой функции и ее второй производной f‘(t), а также вычислим точные значения некоторых n-поперечников классов аналитических в единичном круге функций в весовом пространстве Бергмана. Отметим, что неравенство (3) является распространением результата Н. П. Корнейчука [14] на случай аналитических в единичном круге функций принадлежащих весовому пространству Бергмана Bq,Y, 1 C q C то. Приведем необходимые для дальнейшего определения и обозначения. Пусть X — банахово пространство; S — единичный шар в X; M — некоторое выпуклое центральносимметричное подмножество в X; Лп С X — n-мерное подпространство X. Величины bn(M, Bq,Y) = sup { sup{E > 0 : eS П Лп+1 С M} : Лп+1 С Bq,Y}, dn(M,Bq,Y) = inf { sup{inf{\f - g\\Bq,7 : g G Лп} : f G M} : Лп С Bq,Y} называются соответственно бернштейновским и колмогоровским n-поперечниками. Указанные поперечники удовлетворяют неравенству (см. [16]) bn(M,Bq,Y) C dn (M,Bq,Y )• (4) Пусть Ф(и) — положительная неубыва.ющг 1я функция. определенная для и ^ 0 п удовлетворяющая условию lim {Ф(и) : и ^ 0+} = Ф(0) = 0. Если M — некоторый класс функций, принадлежащий пространству Bq,Y, то через En(M)BqY := sup {En(f )BqY : f G M} обозначим отклонение множества M С Bq,Y от Положим также множества 0 C t C n; t > n • Л2> n. (sin t)* = ^in t, Для любых r G Z+ и n G N определим классы функций {n/n f (z) G B„y : J' Ш(fУ't')вqY dt C Ф (ПП) .
2. Основной результат Теорема 1. Для произвольной функции f (z) G BqY 1 C q C го, и любого заданного h G (0, n/(2n)] имеет место точное неравенство <1 Введем в рассмотрение оператор h ππ F(fa,t) = ^ (fa(t + T) +fa(t - T)) COS ^TT dT. 4h 2h Используя неравенство (2) при R = r = 1, запишем оценку вд к, c n Ewaк-, c 1 (E„ (fa - F Так как fa (t) - f (fa. t) = 4 ) (-fa (t+t )+2/; «> - fa (t - t ))«» At л m 4h 2h то, интегрируя правую часть равенства (7) по частям и применяя обобщенное неравен ство Минковского (см., например, [15]) b У f М dt a b с j Bf (-,t)»p dt. 1 C p < го, будем иметь wa (•) - f (fa, •)!! Bq, y h j (faa‘(t+t ) - fa(t - t )) (1 - sin 2hT) dT Bq, y h с 2 у iif"(^+t ) - fa(^- t)0Bq, 7 (1- sin2hT) dT- Аналогичным образом методом интегрирования по частям получаем IF (fa )IIb, h / (fa (t+т) - fa (t -т)) cos п-т dr 2h 2h Bq,Y h 1 (ПГ) [ (f (t + т) —f(t — т)) sin dт 2 X 2 h 2 h Bq,Y h < 2 (2h Y j "f (t+т)- f (t - т^a,sin 2^т*• Из неравенства (6) с учетом неравенств (9) и (10) и определения модуля непрерыв ности следует, что h C En(f И,. + h C - т )|Bq ,y 0 - Sin2hT)dr 2 h 1 (^Г J ”f(+ т) -f • т ■ sin5hтdr h 1 — sin^т) dт + (^У /ш (f ;2т)B^ π '-^SiП2hrdr/' чем и завершаем доказательство теоремы 1. Знак равенства для функции fo(z) = zn в соотношении (5) проверяется непосредственным вычислением. > Следствие 1. В условиях теоремы 1 справедливо неравенство En(f)b-y < n/(2n) i j Ш(Ц2т )B,Yt (1 — sin пт) dт + n2 n/(2n) jш(f;2т)b,„ sin пт dт . Теорема 2. Для произвольной f (z) G Bq,Y, 1 C q ^ го, и любого h E (0,n/(2n)), n E N, справедливо точное неравенство h п 1 п En(fK.YC 2hn2 ■ П—2 "2 О";2т|BqY (1 — sin2hт) dт h + ( ^ )2 /^2 (f ;2т)Bq, Y sin ^Tdr 0 и знак равенства в (11) реализует функция fo(z) = zn. <1 Введем в рассмотрение оператор h F (fay t) = • -^ / (fa,(t+т)+fa,(t -т)) (1 - sin п-r") dт• 2h п — 2 2h Из неравенства (2) при R = 1 и r = 2 запишем следующее соотношение: En(fк,. < 1 Ив,.,< 1 (Hf- - F (f^B^ + IF Щ)||в, J. (12) Используя вышеприведенное рассуждение, оценим каждое слагаемое в правой части (12). С этой целью разность f"(t) — F(f,t) представим в следующем виде: h fa — F (faa.‘) = — 2h(n — 2) У (f«‘(t + т) — 2fa-'(t) + f"'(t - T)) (1 - Sin 2hT) dT" ^'^ Оценим равенство (13) по норме lf"—F (ОД, q, У h < 2h(nn— 2) / ^f"(t + Т) — 2f"(t)+ f"(t — Т )^B,^ (1 — ^ЗГ)т 1141 Переходим к оценке второго слагаемого в неравенстве (12). Дважды выполняя интегрирование по частям и используя неравенство (8), получаем IF (f" )^B. * q y 7Г 2h ^ п — 2 h У (f"G + т) — 2f"(^) + f"‘(•— т)) (1 — sin2hT) dT 0 Bq, y Л)2 • _A_ 2h п — 2 h У (fa( + T) — f( — T)) COS ^^T dT 0 Bq, Y = (2L V . 2h п — 2 h У(f (•+т) -2f (•)+f (• -т))sin ;2hT dT 0 Bq, Y h < (2h)3 • 7—2 / “f (+т)—2f()+f (•—т>“b,sin2hT dT-0 Складывая неравенства (14) и (15), с учетом (12) и определения модуля гладкости функции, получаем h 1 п 1 En(f)b,y< ^2 ||fa IIb< 7^2 • llf" (* + T) — 2f" (•)+ f" (•— T)Hb. qY 2hn п 2 X h (1—sin 2hT)dT+(2h)2 у 8f (•+т)—2f (.)+f(.—т )Ла 0 * q, y sin — т dT 2h J 7Г ^ 2Ы2 sin "гт) 2h dT + h (2h)2/Ш2 (f;2T)Bq- sin2hTdT . Непосредственным вычислением можно показать, что для функции fo(z) = zn € Bq,Y неравенство (11) обращается в равенство. > Следствие 2. В условиях теоремы 2 справедливо неравенство En(f)BqY 3 (^ ^^^^^^^^г n/(2n) 2n Ш2 (f‘‘; 2t) Bq Y (1 - sin nT) dT o n/(2n) + n2 j Ш2 (f ;2t)Bq,y sin nTdT , o в котором равенство достигается на функции fo(z) = zn € Bq,Y• Теорема 3. Пусть функция Ф(и) для любых A € [0,1], x € [0, п] удовлетворяет неравенству 2Sin2Па 3 УМ 4 Ф(х) Тогда справедливы равенства λ 3 п/2 - (п/2 - 1)A‘ bn (Wtt(r)(y),Bq,Y,R) = dn (W^^r) = Rn 4nr-1 • Ф (n). <1 Соотношение (17) достаточно доказать для случая R = 1. В силу неравенства En(f^.R 3 RnEn(f)Bq, Y и определения класса W^r)^), имеем dn (Wnr)(Ф),Bq,Y) 3 En (Wnr)(Ф),Bq,Y) 3 4nr-1 • Ф (n), и оценка сверху для колмогоровского n-поперечника получена. снизу используем рассуждения работы Л. В. Тайкова [2]. Введем в рассмотрение (n + 1)-мерную сферу полиномов Для получения оценки Sn+1 = (pn(z) : ^Pn^B, 1 q’Y 3 4nr-1 II докажем, что Sn+i С W^r)^). Если m 3 n. то из неравенства ^PnrLtKq^ dt 3 2nr (sin nrr) llPn IlBq.Y получаем π/mπ/m j црП3 ,t)Bq y dt3 2nr hPn^Bq , y j sin nt dt oo = 4пг-1|рп|в7 (1 - cos nn) = 2sin2 nnФ (п) • qY 2m/ 4mn/ Полагая п/m = Ax, п/n = x, из (20), согласно левой части неравенства (16), будем иметь π/m j ^(p^BqY dt 3 2sin2 4m • ф (П) =2sin2 ПА ф(х) 3 ф(Ах)=ф (mm) .(21) o Пусть теперь m > п. Тогда, вновь используя неравенство (19), получаем π/m j Цр^К^ dt = 0 π/n У «(p^t) π/m Bq,Y dt + У Ш(pn?a, t) BqY dt π/n < ■ ' © -1) © (1+2 (m - о)-© < ♦ e Из неравенств (21) и (22) следует, что Sn+i С Wnir)^). Поэтому, согласно известной теореме В. М. Тихомирова [15], получаем bn (Wa \Ф): Bq,Y) ^ bn (Sn+1, Bq,Y) ^ . r-i Ф f~) • (23) 4 IL IL/ Сравнивая неравенства (18) и (23), с учетом соотношения (4) приходим к равенству (17), чем и завершаем доказательство теоремы 3. > Замечание. В [2] доказано, что условию (16) удовлетворяет, например, функция Ф*(и) = un/2. Автор выражает благодарность рецензенту за цепные советы и замечания, использованные в работе.
En(f )Bq, 7 C 2nj
z h
^ (f:. 2T)Bq,Y (1 - ™2hT)dT
0
2h
+ ([ u(f, 2t)Bq-y sin ^T dT
2h 2h
0
и знак равенства в неравенстве (5) реализует функция fo(z) = zn G Bq,Y, 1 C q C го.
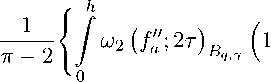
Список литературы О наилучшем полиномиальном приближении функций в весовом пространстве Бергмана
- Тихомиров В. М. Поперечники множеств в функциональных пространствах и теория наилучших приближений//Успехи мат. наук. 1960. Т. 15, № 3. С. 81-120.
- Тайков Л. В. Поперечники некоторых классов аналитических функций//Мат. заметки. 1977. Т. 22, № 2. С. 285-294.
- Двейрин М. З. Задачи наилучшего приближения классов функций, аналитических в единичном круге//Теория приближения функций. Тр. Междунар. конф. по теории приближения функций (Калуга, 24-28 июля 1975 г.). М: Наука, 1977. С. 129-131.
- Айнуллоев Н., Тайков Л. В. Наилучшее приближение в смысле Колмогорова классов аналитических в единичном круге функций//Мат. заметки. 1986. Т. 40, № 3. С. 341-351.
- Фарков Ю. А. Поперечники классов Харди и Бергмана в шаре из Cn//Успех. мат. наук. 1990. Т. 45, № 5. С. 197-198.
- Fisher S. D., Stessin M. I. The n-width of the unit ball of Hq//J. Approx. Theory. 1991. Vol. 67, № 3. P. 347-356
- DOI: 10.1016/0021-9045(91)90009-y
- Вакарчук С. Б. О поперечниках некоторых классов аналитических в единичном круге функций//Укр. мат. журн. 2004. Т. 56. Вып. 9. С. 1155-1171.
- Шабозов М. Ш., Шабозов О. Ш. О наилучшем приближении некоторых классов аналитических функций в весовых пространствах Бергмана B2,γ//Докл. РАН. 2007. Т. 412, № 4. С. 466-469.
- Вакарчук С. Б., Забутная В. И. О наилучших линейных методах приближения функций классов Л. В. Тайкова в пространствах Харди Hq,ρ, q≥1, 0Мат. заметки. 2009. Т. 85, № 3. С. 323-329
- DOI: 10.4213/mzm6633
- Шабозов М. Ш., Миркалонова М. М. Наилучшее полиномиальные приближение функций в пространстве Харди Hp, 1≤p≤∞//Изв. АН Республики Таджикистан. Отделение физ.-мат., хим., геол. и тех. наук. 2009. № 2(135). С. 19-31.
- Шабозов М. Ш., Лангаршоев М. Р. Наилучшее приближение некоторых классов функций в весовом пространстве Бергмана//Изв. АН Республики Таджикистан. Отделение физ.-мат., хим., геол. и тех. наук. 2009. № 3 (136). С. 7-23.
- Вакарчук С. Б., Шабозов М. Ш. О поперечниках классов функций, аналитических в круге//Мат. сб. 2010. Т. 201, № 8. С. 3-22
- DOI: 10.4213/sm7505
- Дзядык В. К. Введение в теорию равномерного приближения функций полиномами. М: Наука, 1977. 511 с.
- Корнейчук Н. П. О наилучшем равномерном приближении дифференцируемых функций//Докл. АН СССР. 1961. Т. 141, № 2. С. 304-307.
- Корнейчук Н. П. Экстремальные задачи теории приближения. М: Наука, 1976. 320 с.
- Pinkus A. n-Width in Approximation Theory. Berlin: Springer-Verlag, 1985. 292 p.


