Автором предложен метод [4], основанный на. том, что непрерывные дроби дают наилучшие рациональные приближения к числу, и на. возможности контролироватв порядок приближения исследуемого числа подходящими дробями как сверху, так и снизу. Важную ролв при этом играет регулярноств поведения неполных частных. При использовании данного метода отпадает нужда в явных представлениях числителей и знаменателей подходящих дробей и, как следствие, расширяется класс чисел, для которых удается получитв точные оценки.

Пусть a — действительное число. В теории чисел и ее приложениях большое значение имеет изучение поведения разности ct

^^^^^^^^.

р

где р — целое число, (р Е Z), q — натуральное число, (q Е N). Поскольку множество рациональных чисел всюду плотно во множестве действительных чисел, то при соответствующем выборе чисел р и q эта величина может быть сделана меньше любого наперед заданного числа. Поэтому представляет интерес изучить относительную малость величины (1), т. е. выяснить сколь малой она может быть, если q не превосходит некоторого натурального числа qo, или, иначе, сколь хорошо действительное число а может быть приближено (апрок-симировано) рациональными дробями в зависимости от величины знаменателя

Поведение величины (1) оценивают следующим образом. Пусть

 0, зависящая от а и функции

^^^^^^^^.

р

< С1^(9)

имеет бесконечное число решений в числах р G Z, q G N.

Порядок приближения p(q") называется наилучшим порядком приближения числа а, если существует постоянная С2 > 0, зависящая от а и <Ду), такая, что при любых р Е Z, д Е N a —

> c2p(q\

—

В нашем изложении мы будем изучать наилучшие рациональные приближения к трансцендентным функциям числа ?Дж)еж. При этом мы будем рас

сматривать арифметические цепные дроби этих функций. В частности, числа вида

6“ + 1

el - 1

а е N

были получены Эйлером [8]; числа лучшие приближения

е2,

2. ea

e к , 2ffc получены Гурвицем [11] наи-

th - a

^^^^^^^^.

Р q

>

с •

In In д у²In д’

установлено Шиокавы [12], а

результаты

th - a

^^^^^^^^.

Р

In In q 6g² In q

P e-- q

>

In In q 3q² In q

получены Такеши [13, 14]. Однако, как установлено Девисом [9, 10] 1) для любого е > 0 неравенство

P e-- q

G -)

In In q q² In q

имеет бесконечно много решений в целых положительных числах р и д;

• 2)    существует число д' = д(г) такое, что для любого ^ € Q

  p e--

  q

  
  

  -G-)

  
  

  In In q q² In q

  
  
  
  

начиная с некоторого q > q';

• 3)    для любого е > 0 неравенство

  e^b —

  
  

  < (c + e)

  
  

  In In д

  q² In д’

  
  

имеет бесконечно много решений в целых положительных р и q. Существует число q' = q(e) такое, что для любого G Q

2 И еь--

> (с-

ln In q 0^1--’ qz In q

начиная с некоторого q > q', где

Г t"1,     2|6

I (46)"1, 2f6.

Нами установлен [4] подход, основанный на том, что непрерывные дроби дают наилучшие рациональные приближения к числу, а также на возможности контролировать порядок приближения исследуемого числа подходящими дробями как сверху, так и снизу. Важную роль при этом играет регулярность поведения неполных частных. В частности, предложенный метод привел к существенному упрощению доказательства теоремы Дэвиса и подобных результатов. При его использовании отпадает нужда в явных представлениях числителей и знаменателей подходящих дробей и, как следствие, расширяется класс чисел, для которых удается получить точные оценки. Отметим, что нижние оценки с худшими константами для некоторых из рассмотренных чисел были известны и ранее (см. [12, 13, 14]).

Сформулируем теорему доказанную в [4].

Теорема. Пусть тц mp sp (? = 1, 2,..., п), натуральные числа;

nmn },

{аи, «12,..., aimi}, {«21, a^y ..., a^Y •, {«ni, «n2, • ., a конечные последовательности целых неотрицательных чисел;

{611, 612, •„, 61_S1}, {621, 622, •„, 62s₂}, •> {6nl, Ку ..., Ь_П813,

{dll, di2, •••, dimiJ) {^21) ^22) •••) ^2тл-2},..,Kl,d,l2,..,dnmJ, конечные последовательности целых положительных чисел, ao Е ^;

a — [a₀; 611, •••, 6i_S1, an + Ac/11, •••, «imi + Adi_mi,..., 6nl, • ••, b_nSm, «nl T Xd_nx, • ••, n T Ас?_итпД_-£,

a = [ao; Wi, W2, W3,..., w^,...]; ii = mi + m2 + ... + m„;

. f О О c = mm < —,—,..., I «11 «12

о

dlmi

dnmn

Тогда для любого е > 0 неравенство a —

- < (c + e) q

In In q q²hq’

имеет бесчисленное множество решений в числах р G Z, q G N.

Существует число q' = q^

такое, что

a —

p i

- > (c q

- ^)

In In q q²hq’

(П)

для всех целых р, q где q > q'.

Далее, пользуясь методом Гурвица [11]

можно доказать, что если

a = [d0; di, d2, «з, •••] разложение a в регулярную (арифметическую) непрерывную дробь, то число вида aa + b ,    ,

• р =------- -, d, о, с, d G

ca + d где ad — be = n > 0 разлагается в регулярную непрерывную дробь.

Однако, отметим, что получение непрерывной дроби по методу Гурвица быстро растет с ростом п и практически трудно решать задачи такого типа. Ниже мы предлагаем другой подход к решению задач подобного типа. В работе нами установлено наилучшее рациональное приближение к числам в цепных дробях.

• 1.    О разложении в цепные дроби чисел вида

ж . til, е* (_Ж € R)

Теорема 1.1. Имеет место разложение

еж + 1 х ‘          1 еж — 1

= 24--- —й------, х G R, х > 0.          (1-1) 6 +          9 X 10 + —---- 14 + ...

<1 Рассмотрим дифференциальное уравнение

W + V = 2»,

(1.2)

решением которого является уравнение

= e2V7 + e-2V7

С другой стороны, из (1.2) следует, что

W + N' = 2V, W" + by"' = V:

• •    ее             •   •   •             •   •   •             •   •   •    •

2ху^^^ + (2n + lVⁿ⁺¹> = 2у^,

• •    ее             •   •   •             •   •   •             •   •   •    •

Решим уравнение для ^- Действительно, и, следовательно,

2 ■ 4— = 2n + 1 + 2х ^(п + 1)

у_ у'

1 х

= 2 + 1Г = у"

5Т

?/	(п+1)
У	(п + 2)
X
X

2+‘"

т. е.

у г е4^ +1 I       х у' ~ e4V+ - 1 “ 2 + 3 х

Заменив Дх на ^, получим из последнего равенства (1.1). >

Теорема 1.2. Имеют место разложения

е« + 1

еа - 1

— (z Т

1        ’

еа + 1

е^ - 1

За + ------ эа + ...

2а +----------j----,

6а 4--

10а + ...

а е N;

а е N;

(1.3)

(1-4)

А — 1

2+;----i—

За Ч--т

10 + ------

7 a + .. .

а C N;

eV ь + 1

е

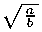
- 1

2 +

a

6b +----^--’

10 ^ 146^777

a, b G N;

eV» + 1

eV» — 1

a b

e ь + 1

e ь — 1

= 2 +

a

2 1 Г” а ’

6 ^           a

10 + —----

14 4- ...

a2

a G N;

—= •

Vb

e Vb + 1

e Vb

^^^^^^^^™

6b2 +--------- a

10+№^

a

7 £ Q

b

2 4               1

6b + --------7---

10 + —--- 14b+...

b e N.

(1-5)

(1-6)

(1-7)

(1-8)

(1.9)

<1 Положим в равенстве (1.1) x = ^ и разделим обе его части на ^. Придем к равенству (1.3).

Аналогично устанавливаются равенства (1.4)-(1.8). >

Теорема 1.3. Пусть t G R^. Тогда е7 = [l;t- l,l,l,3t- l,l,l,5t- 1,1,1,...]             (1.10)

<1 Из разложения (1.1) находим, что ех + 1 _ 21

ех — 1   ж + 61

ж   io

х

Обозначим 7 = + Получим, что е ‘ - 1 = тг 2t

- 1

lot +...

I

Пусть 7о _2f_i ₊ J_   (2t —l)₇i+l — ^   1) + ⁷2₇₁ — 1 + ₇₁+1 — J_ + ₇₁-1 ■ ^>

Примечание. Вместо записи

27о

70 " (21 — 1)71 + 1

t — 1 +

1 +

1 +

71 -

коротко пишем таким образом, что указывали выше.

Находим, что

1    6^72 + 1

71 = 614--= --------.

72       72

Поэтому

- 1

(6t — 1)72 + 1

(31 — 1) +

72 + 1

1 +

72-1

72 + 1

1 +

72 -

Предположим, что для уn_i выполняются условия. Тогда для уп = (4п + 2)1 4-- 7n+i

(4n + 2)#7„₊i + 1

7n+i

получаем

2   _          2_7п+1

7п — 1   ((4и + 2)1 — l)7n+i + 1

(2п 4- 1)1 — 1 +

7n+i + 1 27n+i

1 +

7n+i - 1

7n+i + 1

1 +

7n+i - 1’

и, следовательно, утверждение верно для любого п.

В частности, при t = a £^,a> 1

е² = [1; а — 1,1, 1, За — 1,1, 1, 5а — 1,1,1,...] (Гурвиц, [11]);

при а = |, а Е N

еа

1;-а

-1,1,1,-а

-111--ill а

при t = ^,m,a е N

а е ™

—

а

3 m

5 m

-1,1,1,--1,1,1,--1,1,1,...

а           а

I

(1.11)

(1.12)

(1.13)

Ниже, с помощью нашего метода, мы покажем, что е = [2; 1, 2,1,1, 4,1,1, 6,1,1,...] (Эйлер, [8]),               (1.14)

е² = [7; Зп +2,1,1, Зп +3,1271 + 18]^ (Гурвиц, [11]),      (1.15)

2. е^а

a — 1

5а - 1

+ ЗАа, 6а + 12Аа, —-—

+ ЗАа, 1

ОО л-0 (Г№В'Щ. Ml

(1.16)

Других разложений, в смысле арифметических цепных дробей, числа е ~ до сих пор ненайдено. В связи с этим С. Ленг пишет, что «Общей проблемой является исследование в интересующем нас аспекте значений должным образом нормированных классических функций. Функция с* является, конечно, наиболее простой. Первой возникающей проблемой, и, возможно, самой простой, является определение непрерывной дроби для е^а, где а — рациональное число (или даже произвольное целое). Хотелось бы знать, как особые аналитические свойства одной из классических функций отражаются на арифметических свойствах ее значений». ([3], стр. 97).

Покажем теперь, что имеет место разложение (1.14). В самом деле, в силу (1.12), при а = 1 находим, что е = [1; 0,1,1, 2,1,1, 4,1,1, 6,1,1,...].

Положим п 1 1 l З71 + 2                        5у2 + з

7о = [1; 0,1,1, 71] = ---—г; 71 = [2; 1,1, 72] = х——у.

71 + 1                      2у2 + 1

Следовательно,

371 + 2

1972+11

772 + 4

= [2; 1,2,1,1, 72].

7о = --—х

71 + 1

Предположим, что утверждение верно для 7_n_i. Тогда утверждение верно и для y_n = [2n; 1,1, 7_и+1]. Следовательно, утверждение (1.14) верно.

В силу (1.3) положим а = 1

откуда находим, что

е2 + 1

е2 — 1

1 +---

3 +

1 —  ’

5 + ...

е2 — 7 =

5 +

7+ —-— 9 + ...

Положим

7о = ---р

5 + —

571 + 1

= 0;2,1,1,-

^^^^^^^^™

71 =

1 7+ — =

772 + 1.

72    ’

71-1 2

672 + 1

= [3;272];

272 =

I873 + 2

7з

72 = 9 + —

7з

= 18; у •

97з + 1

7з ’

Предположим теперь, что 73^4.2 выполняется. Тогда

7зп+з — 6п 4- П 4--

73п+4

(6п + 11)7з_и+4 + 1

I

73п+4

Откуда находим

7зп+з _ (би 4- И)7зп+4 + 1

27зп+4

Зи + 5;1,1,^у

^^^^^^^^™

I

Аналогично получаем

73п+4 — 6п + 13 +

73п+5

(6п 4- 13)7з_п+5 4- 1

73п+5

и, следовательно,

73п+4 — 1

(6п + 12)7з_п+5 + 1

27зп+5

Зп + 6;

73п+5

I

Таким образом,

7з_п+5 = 6п + 15 4--

7зп+б

(6п + 15)7з_п+6 + 1

7зп+б

7зп+5 _ (12п 4-30)7з_и+6 4-2

7зп+б

12п + 30;

7зп+б"

I

Рассуждая дальше по п находим, что верно (1.15).

Наконец, докажем (1.16). В самом деле, из разложения (1.1), положив х = ^, 2fa, получим, что eUi ,     1

—---- — а 4         ;---, е а - 1 За +-------

5а 4- ...

откуда, в свою очередь, следует, что

2. е»

-1 =

1 а — 1 4--j----

За 4- —------- эа + ...

Положим

7о =

Q — 1 “Н --

271     ₌

(а — 1)71 4- 1

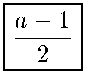
+ 2^

I

71 = За 4--

За72 + 1

Следовательно,

6й7₂ + 2 _

72 _ (5а - 2 -

72      ---

1)7з + (7з + 1) _ Та

---    2 6а 4--;

---   72

72 = 5а 4--

7з

5а7з + 1,

7з ‘

27з

- 1

+

1    7а74+ 1

7з = 7а 4--= --------;

74      74

7з ~ 1

7з + 1

27з (7а-

1 +

7з ~ 1

7з + 1

1)74 + 1 _ 7a

1 +

- 1

+

7з - 1

и вернулись к 71. Предположим, что утверждение верно для уз_п. Тогда

1 ,   1 _ (3 + 6п)а73п+2 + 1

7зп+1 — (3 4- 6п)а 4        — ------------------,

73п+2         73п+2

откуда

27зп+2 —

(6 4- 12п)а7з_п+2 4- 2 73п+2

= (а 4- 12ап) 4-

73п+2

,, , „ х ,    1 5а + бап 73n+3 + 1

7зп+2 = (5 + 6п)а 4--= ------------------

7зп+з          7зп+з отсюда следует, что

7з_п+2   (5а + 6ап)7з_п+з г5а-1          7_3п+3 - 11

” = —— = I” + ^^1111 J

Наконец, находим п х е ,    1 7а + бап 7зп+4 + 1

7зп+з = 7а + бап 4--= ,

73п+473п+4

7зп+з — 1    (7а — 1 4-6ап)7зп_|-4 4-1 г7а —1

---— + Зап, 27зп+4 , 2                  27зп+4             L 2J и, следовательно, утверждение (1.16) верно.

Теорема 1.4. Пусть a — цепная дробь из равенств (1.3)-(1.5), (1.11), (1.14)-(1.16). Тогда, для любого е > 0 неравенство a —

- < (c + e) q

In In q q²ln q'

имеет бесконечно много решений в числах р G N, q G N.

Существует число q' = q^

такое, что

a —

Р q

>

(c-

In In q e)^--’ qz In q

для всех целых р, q,q > q'^Y

—

ae+b | a ce-\-d ’ b "

X

При этом

1) при a =

С g +1 2. е а — 1 Дд е V

а +1 а —1

С = с =

1 2 ’ 1 2а ’

2) <)

при при

a a

_ е g +1 — х е а —1 = е»

с = с =

1 4 ’ 1 2 ’

3)

при

a =

5)

при

a =

е

с =

1 2 ’

6)

при

a

= е2

с =

1 4 ’

7)

при

о =

е» , 2|а

с =

1 4а"

О разложении чисел вида ае, а

Ip — p

Числа

вида, ae, | (a G N) разлагаются в цепную дробь. Для примера докажем следующую теорему.

Теорема 2.1. Имеют место разложения

2е = [5;2,3,2п+2,3,1,2п+2,1]^=0,		(2.1)
Зе = [8; 6, 2, 5, 2п + 2, 5,1, 2п + 2, 5,	1,2п+2,1]”0,	(2.2)
4е = [10; 1,6,1,7, 2, 7, п+2, 7,1, е .	п +1,1]- о:	(2.3)
- = [1;2,2п + 1,3,1,2п+1, е „	ТЗ]”=0,	(2.4)
- = [0;1,9,1,1,2п+1,5,1,2п+1,1 е .	,1,26 + 18п]^=0,	(2.5)
- = [0; 1,2,8,3,1,1,1,п+1,7,1,	ч+1,2]^=о.	(2.6)

<1 Для примера приведем доказательство равенства (2.2). В силу (1.14),

имеем

Зе =

откуда находим

Следовательно,

71 + 3

71-6

З72 + 1

З72 — 2

7з

^^^^^^^^.

75-6

77-6 9

6;

. ’ 3’

7о =

1 о 4

6, -, 3, -, ’ 3     3

6; 3,71

71 =

6З72 + 12

972 + 3

157з+18

57з + 9

3974 + 7

I874+ 7 ~

1375+ 21 = ------------

675 + 9

177б + 3 = ---------------- :

676 + 1

2; 5,1

6;

6;

3, -, 18, -,3, -,3, -,30, -,3, ’ 3    ’3    3    3     3

971 + 18

71 + 3

3’3,72

З72 + 1"

^^^^^^^^.

и

I

I

I

18;

71 + 3

^^^^^^^^.

6?

?• 5 —

’ 5’ 9 1

7з

374 - 21

2; 5,1,

^^^^^^^^™

4572 + 9

672 + 1

г 4

I

72 = [3,3, -,7з

18;-,3,74

г8 „ 1

74 = ^;3, -,75

= [2;1,5,76], 76 =

77 = [42; -,3,78

_ 7578+ 13 _

“ 1878 + 3    .

3      679 + 9

4; 5,1,

З78 — 2"

^^^^^^^^.

2   2979+ 45

^+Ё79±9

—1  679 + 9

75 = 30;-, 3,76

' 1 1 4;3,-,77

2617s+ 45

678 +1

Г16

7s =

L 3

1 +

З73 + 5

З73 + З’

11774 + 21

674 + I ’ 17₇₅+27

' 675 + 9 ’

_ 1897₆+ 33

676 + 1 ’

4; 5,

1,

^^^^^^^^.

з, 3,79

679 + 1

₌ II79 +17 2₇9+3 ’

—,   1

5 + —.

Предположим, что утверждение верно для 7бп+2- Тогда для 7бп+з находим

7бп+з —

7бп+4 —

18 + 36п;-,3,7бп+4

г8 + 12п

4п + 2; 5,

i 3, —, 7бп + 5

(117 + 216)7бп+4 + (21 + 36п)

1 37бп+4 ’         3

^^^^^^^^.

б7бп+4 + 1

(17 + 24п)7_6п+5 + (27 + 36п)

б7бп+5 + 9

откуда следует, что

37бп+4 — 2 _ (13 + 24п)7бп+5 + (21 + Збп) _ г          7бп+5 — 6"

3                   67бп+5 + 9              L            ’     9 J

Аналогично, имеем

7бп+5

7бп+5 — 6 9

7бп+б

7бп+7

7бп+7 ~ 6 9

7бп+8

Г 1

= 30 + 36п,-,3,7бп+б

(189 + 216п)76п+6 + (33 + 36п) б7бп+б + 1

(153 + 216п)7бп+6 + (27 + Збп) Го , „ , с

=----------Г -------771----------= 2 + 4n, 1, 5, 7бп+б ,

547_6п+6 + 9

= 4 + 4п; 3, |,7бп+7] = [4 + 4n;5,1, ^^—,

' ™ 1 „

42 + Збп, - ,3,76и+8

(261 + 21бп)76п+8 + (45 + 31п) б7бп+8 + 1

(225 + 21бп)76п+8 + (39 + Збп)

547бп+8 + 9

г!6 + 12п   1

о ’ 3, ~, 7бп+9

4 + 4п;5,1,

7бп+8 ~ 2

(11 + 8п)7бП4-9 + (17 + 12п)

27бп+э + 3

откуда, наконец, находим

37бп+8 — 2 _ (25 + 24п)7би-|-9 + (45 + Збп)

4 + 4п, 1,5, -^^

3                б7би+9 + 9

Таким образом, получим разложение

Зе = [8; 6, 2, 5, 4п + 2, 5,1, 4п + 2, 5,1, 4п + 2,1, 5, 4п + 4, 5,1, 4п + 4, 5,1,4п + 4,1,5]“ о = [8; 6, 2, 5, 2п + 2, 5,1, 2п + 2, 5,1, 2п + 2,1]-0.

Аналогичным образом доказываются равенства (2.1), (2.3)-(2.5). >

Теорема 2.2. Имеет место разложение

Зе г

- =[4; 12,1,10,1,11, 2,1, 2, 2,1, 2, 2,1,1,1,1,1, 2, 2, 2,11,1,1,1,

(2.7)

11, 2п + 3,11,1, 2п + 2,1,1, 2, 2, 2п + 3, 2, 2,1,1, 2п + 3,

1,1,2,2,2п + 4,11,1,2п + 3,1]- 0.

• <1 В силу (2.2), применим сюда разложения

Зе г                    1    5         5    5           11

• - = 4; 12,1,10,1,10, - 4, -, 2,1, 2, -, 8, -, 2, 2,10,-, 8, -, 10, 3,10,

• 12,    2, 3, 2,    16,    2, 4,10,1,16,1,10, 5,10,    20,    2, 5,(2.8)

Z Z         z z          z zz z

5 5111

2,-, 24, -,2,6,10,-, 24, -,... .

Рассмотрим теперь разложения

7o = [10; l,7i], г    1    5   1    36472 + 136 r

7i= 10;-, 4,-,7з =             = [П; 2,1,2,7а],

L     z    z   J 0272 + 12

72 = [2; 1, 2,7з]

7з =    8 5 2   1 = 52474 + 220 =

'     (2    2 J 20074 + 84 L

74 = [2; 75], rill 14076+ 232 r

75= 10,-, 8,-, 76 = 19'\9n =[H; 1,1,1,76 + 1],

L 2    2 J 1276 + 20

76 + l = [10;3,77] + l = [H;3,77],

HO г 1

77 = [10; -

Г5

79 = 7’16

5 12,-,7s

5 „      "

2> 2, 7io

84478 + 328

7278 + 28

[11; 1,2,1,1,2,7s],

10047ю + 420

3927ю + 164

= [2; 1,1, 3,1,1,2,2,740],

710 = [4; 711], г 1        1

711 = [10;-, 16,-,712

2З6712 + 421

20712 + 36

= [11; 1,3,1,712 + 1],

712 + I = [10; 5, 713] + 1 = [11; 5,1, 713].

Следовательно, г 1       5

713 =[10;-, 20,-,714

714=[2;5,2,7i5],

Г5 _ 5 „    1

715 — [-; 24, -, 2, 716

1324714 + 520 г

112714 + 44 -[И;1’4,1,1^,^],

14847i₆ + 620

I

5847i₆ + 244

Аналогичные рассуждения дают, что

715 = [2; 1,1, 5, 1,1, 2, 2, 716],

716 = [6; 71?]:

Г    1          1    332718 + 616 г

71₇= 10;-,24,2, 7i₈ = ^П8 = [11; 1, 5,1, ₇18 + 1],

L    2          J            + uZ

712 + 1 = [11; 5,11,1, 4,1,1, 2, 2, 5, 2, 2,1,1, 5,1,1, 2, 2, 6,11,1, 5,1, ₇is + 1]. (2.9) Применив теперь к общему разложению ^, разложение аналогичное (2.8) и (2.9), придем к цепным дробям (2.7).

ЗАМЕЧАНИЕ. Аналогичные доказательства проходят для чисел вида. a,b Е N.

Теорема 2.3. Имеет место разложение

39е + 10

15е + 4

3ei г

2; 1,1, 2, 2,      = [2; 1, 1, 2, 2, 4, 12, 1, 10, 1, 11, 2, 1, 2, 2,

1,2, 2,1,1,1,1,1,2, 2, 2,11,1,1,1,11,2п+3,11,1,2п + 2,1,1,2,    (2Л0)

• 2 , 2тг + 3, 2, 2,1,1, 2тг + 3,1,1, 2, 2, 2тг + 4,11,1, 2тг + 3,1]“₌₀

Аналогичное разложение имеют и числа вида ^^

<1 Рассмотрим разложение

39е + 10

15е + 4

2+----1—1 +——1 +—г

2 + -д—

2е откуда, следует требуемое разложение (на. основе (2.7)). >

Ниже мы покажем, что имеют место разложения е + j, а £ Z, 6 Е N.

Теорема 2.4. Имеет место разложение

• 3    _г

е + - = [3; 2, 7, 2,1,1,1,1,1,1,1, 2,1,2,1,1,1,1, 31, 3,1,1, 2, 5,1,1, 4,3,

1,1, 2, 3, 7,1, 2, 3,1,1, 2, 2, 2,1,1, 3, 2, 3,1,1, 2, 2, 31, А + 1,1, 3,1,1, (2.11)

2,1, А+1,4,1,1,3, А+1,1,3,1,1, 2,1, А+1,2, 7,1,1, А+1,1,3,

1,1, 2,1, А+ 1,1, 2,1,1, 3,1, А+ 1,1, 3,1,1, 2,1, А+ 1,1]^0

<1 Как известно,

е+~ — 2 4--

4 1 +

2+;——

4 + ...

7^

1    ! 3 ₌ 15_7о + 11 _{= 3} , З70 " 1

_{х +} 1   4    470 + 4     ⁺ 470 + 4'

7о

Определим 70

= [2; 1,1,71]

= 2^+1 ¹¹ подставим его значение в выражение

^о

370 -1

470 + 4

.571 + 3

о------- — 1

271 + 1

4^ + 4

271 + 1

1371 + ⁸ - ₂ ,     ²71

2871 + 16       1З71 + 8

Определим в общем виде

7п — 2п + 2 +

1 + 7i

7n+i

(4n + 5)7„₊i + (2п + 3)

27n+i+ 1

I

(2.12)

Получим, что

Л1 =

Аз —

Аз —

271	о 972+5 272+1	_ 1872+ 10 - 1ЗЗ72 + 23 “ 1—
1371 + 8	13-+S + 8
	=    47^+4 1 772 + 3	ПП З72 - 1 = 1 + -------, 472 + 4
З72-1 -----= 472 + 4	377з + 20 _ 607з + 32 ” L	■л    327з + 12 _ J  377з + 20 “ U
=	1     Э7з + 4 147з + 8	^т+Ё21±4^г 973 + 4
47з  _	6874 + 36 п- 9З74 + 49 " U	2574 + 13 _ 2 6874 + 36 Ы
57з + 4
=	1 ।   7^ + 3 Ы 1874+10	= о , +4 + 4 -U 774 + 3

1874 + Ю Ь 2574+ 13

—1  474 + 4

+

+

772 + 3

1872 + Ю

147з + 8

237з + 12

47з

57з+ 4:

Л4 —

З74 — 1

474 + 4

61 + 75 + 32 _     3175 + 16

9275+ 48 "U+6175 + 32

1 4

ЗО75 + 16

3175 + 16

1 4

3075+ 16’

3075+16

2576 + 13          77б+ 3

7827б + 406 ----|+ 2576 + 13

, 476 + 4

+ 776 + 3

—1 476 + 4

Л8 —

Лб= 376^7

47е + 4

д З77 + 4

Л7 — --7---

З78 — 1

47s + 4

Л9 —

-410 —

8577 + 44

12477+64

5 +

777 + 4

1 +

3977+ 20

8577 + 44

2 +

777 + 4

3977+ 20

1 +

З77+ 4

10778 + 55 _ гул 2578 + 13

13278 + 68 " U + 10778 + 55

4 +

778+3

2578 + 13

3 +

47s + 4

778 + 3

1 +

З78 — 1

478 + 4’

10979 + 56 _ гул 4779 + 24

15679 + 80 =     10979 + 56

I ¹⁵79 + ⁸ ₌Ы,    ²^

+ 4779+ 24  ^+ 1579 + 8’

1579 + 8

82710 + 42

631710 + 323

7 +

57710 + 29

82710 + 42

1 +

25710 + 13

57710 + 29

2 +

7710 + 3

25710 + 13

3 +

4710 + 4

7710 + 3

1 +

З710 - 1 4₇ю + 4’

З710 — 1

4710 + 4

133₇₁₁ +68 _ гул    55711 + 28 ₌ ^п   23_7п + 12

I88711 + 96 " U 1ЗЗ711 + 68 " U  55711 + 28

2 +

9711 + 4

237и + 12

2 +

57п + 4

9711 + 4

1 +

47п

57ц + 4

1 +

711 + 4 47п

Ли — —i--- 4711

57₇i2 + 29

196712 + 100

7   25712 + 13

-1  57712 + 29

7, 7712 + 3

25712+ 13

7 4712 + 4 _

7712 + 3

7 ,3712-1

4712 + 4

З712 - 1

Al 2 — --------7

4712 + 4

157713 + 80

22O713 + 112

1 +

6З713 + 32

157713 + 80

2 +

31713 + 16

6З713 + 32

2 +

3171з + 16

Определим теперь выражения вида Л 13+8+ .. . ,Л₂о+84 (1 = 0,1,2,...). С этой целью определим сначала, в силу (2.12),

?13+8t —

(57 + 321)714+84 + (29 + 161)

2714+84 + 1

714+84 —

(61 + 321)715 +84 + (31 + 161)

2715+84 + 1

715+84 —

(65 + 32^716W + (33 + 16^)

717+84 —

2716+84 + 1

(73 + 32t)7i8+8t+ (37+161)

716+84 —

(69 + 321)717+^ + (35 + 161)

719+84 —

2718+84 + 1

(81 + 321)720+84 + (41 + 161)

718+84 —

2717+84 + 1

(77+ 321)7i9+8t+ (39+ 161)

2720+84 + 1

720+84 —

2719+84 + 1

(85 + 321)72i+8t + (43 + 161)

2721+84 + 1

।

Теперь находим

л            713+84

Л13+84 - —------—7

31713+84 + 1

(57+ 321)714+84 + (29 + 161) (1799 + 9921)714+84 + (915 + 4961)

31 +

3287i4+84 + 16

(57+ 321)714+84 + (29 + 161)            1

2 5714+84 + 13

3 2714+84 + 16

Р| _|_ 7714+84 + 3

2 5714+84 + 13

■pi 4714+84 + 4 _

7714+84 + 3

+

3714+84 ~ 1

4714+84 + 4 '

З714+84 - 1

Лы+84 - ------—

4714+84 + 4

(181 + 961)715+84 + (92 + 481) (252 + 1281)715+84 + (128 + 641)

+

(71 + 321)715+84 + (36 + 161) ₌ (181 + 961)715+84 + (92 + 481) “

pi (39 + 321)7+(20 + 161) (71 + 321)7+(36 + 161)

+

327 + 16

+

(39 + 321)+ (20 + 161)

3715+84 + 4

4715+84

327 + 16

"П 47

4 +-----

-1 77+ 4

,     _ 3715+84 + 4

^15+84 — ---------

4713+84

(203 + 961)7i6+8t + (103 + 481) (260 + 1281)716+84 + (132 + 641)

р (57 + 321)7+(29 + 161) _ (203 + 961)7+ (103 + 481) =

3 +

327 + 16

(57 + 321)7+ (29 + 161)

327 + 16

-1  257+ 13

—  4+ + 4

3 + —--=

-1 77+ 3

pi 3716+84 — 1

4716 +84 + 4’

_ 3716+84 - 1

7116+84 — +-------~7

4716 +84 + 4

(205 + 96t)7i7+84 + (104 + 487) (284 + 128^)717+84 + (144 + 6 47)

^   (74 + 32^)7+ (40 + 167) _

+ (205 + 96^)7 + (104 + 487)

yi (47 + 32£)7+(24 +Ш) (79 + 32^)7+ (40 + 167)

1 +

32^ + 16

(47 + 32£)7+ (24 + Ш)

^^++1±1=

327 + 16

yi 27i7_W "    15717₊84 + 8’

_   2717+84   _   (146 + 64^)718+84 + (74 + 32^)

17+84 - 15717+84 + 8 - (1111 + 480^)718 +84 + (563 + 2407)

+

(89 + 32£)7 + (45 + Ш) _ (146 + 647)7 + (74 + 327) =

^  (57 + 327)7 + (29 + 167)

(89 + 327)7 + (45 + 167)

+

32^ + 16

(57 + 32£)7+ (29 + Ш)

^^7ТП+^т±+, L------11 327 + 16

-1  257+ 13

+

47 + 4 _

77+ 3 =

"П 3718+84 - 1

4718 +84 + 4 ’

_ 3718+84 - 1

7118+84 — +-------~7

4718 +84 + 4

(229 + 96^719+84 + (116 + 48<)

(316 + 128t)7i9+8i + (160 + 64t)

+

+ 44 +

+ (229 + 967)7 + (116 + 487)
+	327+ 16
	(55 + 327)7 + (28 + 167)
+	57 + 4 = 1      4719+84 97 + 4        5719+84 + 4

yi (55 + 327)7 + (28 + 167) (87 + 327)7 + (44 + 167)

1 327 + 16

1 +

97 + 4

237 + 12

-419+84 —

4719+84

5719+84 + 4

(324 + 128^)720 +84 + (164 + 647)

(413 + 16О7)72о+84 + (20 9 + 807)

0; 1, 3,1, 7 + 1,1, 3,1,

4720+84 + 4"

3720+84

^^^^^^^^.

1J ’

.        З720+84 — 1

7120+84 - -------—7

4720+84 + 4

(253+ 96£)72i+84 + (128 + 487) (348 + 1287)721+84 + (176 + 647)

0; 1, 2,1, 7 + 1,1,

3 1 721+84 + 16"

I

L                       721+84 J

Отсюда, по индукции, следует утверждение теоремы (2.4). >

Примечание. Очевидно, что числа вила ^е ^ ^, a,c Е ^, b,d Е представить в виде непрерывной арифметической дроби.

N, можно

Теорема 2.5. Пусть a —цепная дробь из равенств (2.1)-(2.7) (2.10), Тогда для любого е > 0 неравенство

(2.11).

a —

- < (c + e) q

In In q q² In q’

имеет бесконечно много решений в числах р Cl. q СЕ*. Существует число q' = q(e) такое, что р Е Ъ, q G N

р a-- q ,       х In In q > (C £) 21 q2 In q для всех целых р и q верно q > q' (е\ При этом

1)

при

a =

= 2e

c =

= 1,

2)

при

a =

= 3e

C =

= 1-

3)

при

a =

= 4e

C =

= 2,

4)

при

a =

= f4

c =

= 1,

5)

при

a =

= 3

C =

= c

6)

при

a =

= 4

C =

= 2,

7)

при

a =

= ^

c =

= 3,

8)

при

a =

_ 39e+10 15e+4

C =

= 3,

9)

при

a =

= 6 + 4

c =

= 8.

3. О разложении чисел вида ае2, a 1е2, ab 1е2, (ае2 + 6) (се2 + d) \ е2 +

Имеют место разложения ae², а ¹е², ab ¹е², a,b Е N. Как и в параграфе 2 приведем доказательство для случая 2е², |е², |е².

Теорема 3.1. Имеют место разложения

2е2 = [14; 1, 3,1,1 + Зп, 36 + 48п, 2 + Зп, 1, 3, 3 + Зп, 60 + 48п, 4 + Зп]”=0 (3.1)

-е2 = [2; 2, 6, 3,1, 5 + 8п, 2,1,1 + 2п, 5,1,1 + 2п, 2,1, 9 + 8п,

2,1, 2п + 2, 5,1, 2 + 2п, 2,1]^0

2 9 г                                                                     ---------------------------------

-е² =[4; 1,12,1,1,11,1, 3,1, 2, 3, 2, 38, 2,11, 2, 2, 27 + 16n, 1,2,1 + п,

1,1, 2, 2,1 + n, 1, 2, 35 + 16n, 1, 2, 2 + п, 11,1,1 + n, 1, 2]“=о

<1 Из разложения (1.15) находим, что

9     r            1               1                     1 1

2е2 = [14; 1, 2, -, 6, 9,10, -, 2, 3, 60, 4, 2, -, 18, 21, 22, -, 2, 6,108, 7,...].

Определим

75n+l; 7бп+2, 7бп+3; 7бп+4, 7бп+5;   (^ О, 1, 2, ... ).

?5п+1 —

2; ^’ 75п+2

3; 1 +

4       "

75п+2 — 2 J

75п+2 = [6 + 12п, 9 + 18п, 75п+з] =

G55j_J+On4_H4n^

(9 + 18п)75_п+з + 1

75п+2 - 2 _ (37 + 256п + 144n²h_5n+3 + (4 + 12п) г          । ю 7бп+3]

----:--- = --------тхл. ---—--------:-------- = Зп + 1; 36 + 48п, —■—

4                (36 + 48п)75_п+з + 4            I                   4 .

7бп+з —

7бп+з

10 + 12п;-,75п+4

(12 + 12п)75_п+4 + (20 + 24п) 75п+4 + 2

(12 + 12п)7_5п+4 + (20 + 24п) 475п+4 + 8

— [Зп + 2; 1, 75,l+4 + 1],

7_5п+4 = [2; 3 + Зп, 75п+б], 75^+4 + 1 = [3; 3 + Зп, 75^+5],

75^+5 = [60 + 48п; 4 + Зп, 75п+б]-

Отсюда, по индукции, следует требуемое разложение (3.1).

Докажем теперь (3.2). На основе разложения (1.15) напишем, что

г2

г7 1   , _ _

-;6,-,3,1,54 + 72п,

5 + 6п

24 + 18п, |,3,3 + 2п

’       2

ОО

I

,3, -,18 + 18п, 10 + 8п,

- п=0

Положим

7о - о + -

3   71

771 + 3

З71

-21 ⁷¹⁺³

"      371 '

71 =

6; |, 3,1,72

5472 + 4

772 + 6 ’

/ 71 +3 ^ ¹ _ / 7572 + 63 ^ ¹ _ г         72 - 6 "

V З71 )      V6272 + 135/ Г’ ’ ’ ’   9 .

72 = 54;-,7з

2737з + 162

5₇з + 3 ^:

= [5; 2,1,1,7з],

Г 1         1   117674 + 117 г                72-6

73= 3;-,18,10, 74 =                = 5; 1,1, 2,1, 9, 2,1,

Применим метод индукции. Положим, что

7зп+2 = 54 + 72п;

5 + 6п

, 7зп+з

Г 1

7зп+з = [3; -, 18 + 18п, 10 + 8п, 7Зп+4

7зп+4= [24 + 18п;-,3,3 + 2п,7Зп+5

п = 0,1,2,...

Далее, находим

7о = 2 +

71 + 3 _      757₂ + 63

37!    " + 16272 + 135

2; 2, 6, 3,1 +------

72-6

" = [5; 2,1,1,7з], 7з = [5; 1,1, 2, 9, 2,1,

g               L 7         7    7

Вычислим 2зл^ —б (7 _этой целью найдем

73п+2 —

(273 + 684п + 432п²)7з_п+з + (162 + 216п) (5 + 6п)7з_п+з + 3

7з_п+2 - 6   (243 + 648п + 432п²)7з_п+з + (144 + 216п)

9    “          (45 + 54п)7з_п+з + 27

= [8п + 5;2,1,1 + 2п,7Зп+з]:

„     _ (1176 + 2016 + 864п²)7з_п+4 + (117 + 108п)

^73п+3 - (211 + 348п + 144п²)7з„₊4 + (21 + 18п)

= 5; 1, 2 + 2п, 2,1, 9 + 8п, 2,1, 73п+4 ~ 6],

_ (486 + 648п + 216п²)7з_и+5 + (153 + 108п)

73п+4 —

(19 + 12п)73п+5 + 6

7зп+4 - 6 _ (372 + 576п + 216п²)7з_п+5 + (117 + 108п)

(171 + 108п)7з_п+5 + 54

2 + 2п; 5,1, 2 + 2п, 2,1,       ----

Отсюда следует равенство (3.2).

Наконец, докажем равенство (3.3). С этой целью к разложению (3.2) применим разложение

Iе2 -

13 + 8n „ 1      „ 5    3 + 2n

---------, 4,    6 + 4n, -, 2,-------, 2      , , 2’            ’ 2’ ’      2

3 5  15  11       1

4; 1,12, -, 2, -, 4, -, 2, -, 2, -, 4, -, 18,1, 2,1,10, -, 4,1, 2,

Z    Z    Z Z    Z Z                 z

4, -, 34 + 16n, 1, 2, 2 + n, 10, -, 8 + 4n, 1, 2

1 oo

- n=0

I

Положим

ГЗ „

7o = ^2’2,71

4₇i + 1

272-1 2

^И1'4^1!’

+ . 1 „

71      2 ^’ 2 ’ ^’ 7

2772 + 8

1072 + 3’

П872 + 35

IO72 + 3

97з + 10 --— =

473 + 4

ii; 1,3,1,

272 -

^^^^^^^^.

o 1

72      2 ’ ^’ 2 ’ 7^

2;3,

7з + 2"

7з

^^^^^^^^.

2 J

7з =

4; |, 18, 1,2, 1,74

_ П73 + 12

= 47з + 4 ’

46674 + 230

7874 + 39 ’

7з + 2 73-2

62474 + 308

ЗО874+ 152

= [2; 38, 2, 74],

74= [10;-,4,1,2, 75

rl3

22875+ 80 r

+о++Г = 11112'2'4^ + 11-

75 = ^T’4, 2’6,76

475 + 1 =

Г5 . 3

76      2 ’ ^’ 2 ’ 7^

6107g + 83

2276+ 3 ~

_ 2З77+ 12

~ 877 + 4 :

14776+ 20

2276 + 3 ’

2^6 " 27; 1,2,1,1,1,^

276 -1

77 = [4+з4,1,2,2,78] = ^±+1

’ L ’ 2 ’ ’ ’ ’ ’ ' J 5077s+ 217

Г 1

78= [10;-,8,1,2, 79

Аналогично, находим

75+4n —

^^^^^^^^.

?

2; 2,1,1,

77 + 21

^^^^^^^^.

2 J ’

= [2; 35,1,2,2,78],

37279+ 128 r

₄₉'\₁₉ =[H; 1,1,1,2, 4₇₉ + i].

З279 + 12

г 13 + 8n Л 1 л ---о---, 4, - , 6 + 4n, 76+4n

76+4,4

[^

(147 + 168n + 48п2)7б+4п + (20n + 12) (22 + 12)7б+4п + 3

3 + 2n

---2---> 77+4,1

(46 + 24n)77+4n + 24

(16 + 8n)77+4n + 8

?8+4п

?7+4п —

4; -, 34 + 6n, 1, 2, 2 + п, 7§+4и

_ (1514 + 1320п + 288п²)7₈₊4п + (648 + 288п)

“  (257 + 222п + 48n2h8+4n + (ПО + 48п) ’

10;|,8 + 4п,1,2,79+4п

(372 + 144п)7_9+4п + (128 + 48п) (32 + 12п)7_9+4п + (11 + 4п)

Путем разложения в цепные дроби находим

_ (610 + 684п + 192п2)76+4и + (83 + 48п) 75+4п+             (22 + 12п)7б+4п + 3

= 16п + 27; 1, 2, п + 1,1,1, 27б+4п ~ Х],

27б+4п ~ 1 _ (38 + 20п)77_+4п + 20 _ г            77+8п + 2 "

2           (16 + 8п)77-|__4п + 8      - ’ ’       ’ ’ 77_+8п — 2. '

77₊4п + 2 _ (2028 + 1764п + 384п²)7_8+4п + (868 + 384п) 7_7+4п - 2 - (1000 + 876п + 192п²)7_8+4п + (428 + 192п)

= [2;16п + 35,1,2,2 + п,78+4п],

78+4п = [11; 1, n + 1,1, 2, 479+4п + 1].

Отсюда, по индукции, следует требуемое разложение (3.3). >

Теорема 3.2. Имеет место разложение

24е2 + 15

10е2 + 6

= [1; 1, 2, 2, 4,1,12,1,1,11,1, 3,1, 2, 3, 2, 38, 2,11, 2, 2,

16п + 27,1, 2, n + 1,1,1, 2, 2, n + 1,1, 2,16п + 35,

(3.4)

<1 Разложение

1,2,2 + п,11,1,п+1,1,2]~=0

24е2 + 15 _1

10е2 + 6        .1

1 +1

2 42

2+-е2

дает требуемое разложение (на основе (3.3)). >

Теорема 3.3. Имеет место разложение е + - = [7; 1, 8, 73,1 + Зп, 2,1,1,1,1 + Зп, 120 + 192п, 2 + Зп, 7,

1,1 + Зп, 1,1, 41 + 48п, 1,1,2 + Зп, 2,1,1,1,2 + Зп,           ^3’5^

1,1, 53 + 48п, 1,1,3 + Зп, 7,1, 3 + Зп, 264 + 92п]”=0

<1 Из разложения е2 = [7; Зп + 2,1,1, Зп + 3,12п + 18]“=0

= [7; 2,1,1, 3,18, 5,1,1, 6, 30, 8,1,1, 9, 42,11,1,1,12, 54,14,1,1,15,16,...]

последовательно находим

7о = [7; 2,1,1, 3,18, 71] =

24317! + 133

3297!+ 18

„   1 _ 519171 + 284

70 + 2 “ 65871 + 36

7; 1,8, 73,^],

71 = [5; 1,1, 6, 30, 72] =

217172 + 72

39272 + 13 ’

217172+ 72

156872 + 52

1; 2,1,1,1,1,120,^,

72 = [8,1,1,9,42,7з]

6827з+ 162

8OO73+19 ’

7з   6827з + 162   г                   7з-21

= ____ = 2-711114111 —__

4    З2ОО73 + 76    L                        4 J

7з = [П; 1,1,12, 54, 74]

1557574+ 288

135274+25

7з - 2 _ 1287174 + 238

74 — 2

2; 2,1,1,1,2,1,1,53,1,1,21—

4   - 540874 + 100

2972975 + 450

20487s+31

74 = [14; 1,1,15,66,75] =

74 - 2   2562375 + 388 г            751

------ = --------------- = 3; 7, 1, 3, 264, — .

4        819275 + 124     [ ’ ’ ’ ’     ’ 4 J

Применим метод полной математической индукции. Введем предварительно оценки по п = 0,1, 2,...

74_п+1 = [5 + 12п; 1,1,6 + 12п, 30 + 48п, 74^2], 74п+2 = [8 + 12п; 1,1,9 + 12п, 42 + 48п, 74„₊з], 74п+з = [П + 12п;1,1,12 + 12п,54 + 48п,74п+4]: 74_п+4 = [14 + 12п; 1,1,15 + 12п, 66 + 48п, 74,^5].

Далее находим

1      _ (2171 + 1212071 + 22464п2 + 1382п3)74п+2 + (72 + 288п + 281п2)

474n+1 -        (1568Т5Т76пТ46^^

= 1 + Зп; 2,1,1,1,1 + Зп, 120 + 192п, ^±^ ,

1      _ (682 + 25944п + 32832п2 + 13824п3)74п+3 + (162 + 432п + 288п2)

474п+2 -        (32ЖТтб80пТ4608^^

• = 2 + Зп; 7,1,1 + Зп, 1,1, 41 + 48n, 1,1, ^71п^ ~ ² ,

  7_4п+3 - 2   (12871 + 39960п + 40896п² + 13824n³h_4n+4 + (238 + 528п + 288п²)

• 4    -           (5408 + 9984n + 4608n²h_4n+4 +(100 + 96п)

= 2 + Зп; 2,1,1,1,2 + Зп, 1,1, 53 + 48п, 1,1, 74п+4 ~ 2 .

Отсюда находим

74п+4 - 2   (25633 + бЗОООп + 51264п2 + 13824п3)74п+5 + (388 + 672п + 288п2)

• 4    -           (8192 + 12288п + 4608n²h_4n+5 + (124 + 96п)

= 3 + 3п;7,1,3 + 3п, 264+ 190п, ^^ .

7_4п+5 получаем из 7_4n+i, заменив п на п + 1.

Таким образом, из разложений 70, 71,72, .. . находим разложения в цепную дробь (3.5). >

Теорема 3.5. Пусть a — цепная дробь из равенств (3.1)-(3.5). Тогда для любого е > 0 неравенство a--< (с + е)

In In q q² In q

имеет бесконечно много решений в целых числах p,q G N. Существует число q' = q(y") такое, что a

^^^^^^^^™

р q

> (с-

. In In q

- qz In q

для всех целых р, q таких, что q > q^e).

При этом

1)	при	a	= 2е2	с =	1 8 ’	2) при a =	^е2 3 е	С = u 4 ’
3)	при	о	= ^е2 3 е	с =	3 8 ’	4) при a =	24е2+15 10е2+6	с = — с     8 ,
5)	при	о	= е2 + |	с =	1 16 ‘