О некоторых краевых задачах для одного смешанного уравнения с разрывными коэффициентами в прямоугольной области

В явном виде найдено регулярное решение краевой задачи для одного смешанного уравнения с разрывными коэффициентами в прямоугольной области.

Рассмотрим уравнение u$x + Uyy + р3и + /о,            У > о,                        (1)

и_п - (-y)^mMyy + P2Uy + p₃u,  у < 0, m = 0,1

в области Q, ограниченной отрезками А_ОА'_О, А'_ОВ'_О, В'₀В₀, В_оА_о прямых ж = 0, у = h >  О, ж = /, у = —а (а > 0). Обозначим через Qi = И А (у > 0) и П₂ = ^ А (у < 0) эллиптическую и гиперболическую части области И соответственно. Пусть АВ — открытый интервал (ОД) при у = 0; АВ₀ : ж + 2Ц—у = 0; ВА₀ : ж — 2Ц—у = I — характеристики уравнения (1) при у < 0;/₀ = const > 0; pi, р₂ = const, причем р₂ < 1.

Задача (А). Найти регулярное в области Я решение иД,у^ уравнения (1), непрерывное в замкнутых областях Qi и Я2, дважды непрерывно дифференцируемое в областях Qi и Я2 и удовлетворяющее краевым условиям

Дщ = (атж - Дм)|ж=0 = ф0(у), -а  у  Д(2)

Д2м = (а2щ, + Дм)|^=; = фг(у), -а < у

R3u = (a3uy + Дп)|у=л = Фн^, 0 < ж < Z;(4)

иД, —а) = ф_Дтф 0 < ж < I,(5)

где а^Д — постоянные, причем а» + Д Д 0, г = 1,2,3.

В зависимости от значений ащД,щ (г = 1,2,3), свойства функций ф₀, уд, гД, ф__а будут определены каждый раз.

Пусть ад = 0, Д = 1 (г = 1,2,3), /0 = 0, m = 1, р3 = 0, р2 Д 0 и выполняются условия склеивания lira иД,у) = lira (—у)Р2-1м(ж, у),                         (6)

• У^0+        улО-

• 11m м„(ж,у) = lira (—у)Р2му (ж, у).                         (7)

у^0+         улО-

Решение задачи (1)-(7) будем искать в виде суммы иД,у) = мх(ж,у) + и₃Д,уф где, в свою очередь, функция м₂ имеет вид мх(ж,у) = Гг(ж,у) + П1Д,уф

• (с) 2002 Елеев В. А., Жемухова 3. X.

Здесь Ух(ж,у) — решение задачи:

У1жж + ^iyy + P1V1 = 0;(8)

^(0,у) = 0, ^(г,у)=0, О^уО;(9)

У1(ж,/i) = ^(ж), 0 < ж < I,(10)

а Их(ж,у) — решение задачи:

Uixx — Uiyy + P1U1 = 0;(8')

^1(0,у) = ^о(у), E7i(Z,y) = уг(у), 0 ^ у ^ h;(9')

П1(ж,/г)=0.(10')

Решение и2(ж,у) ищется в виде суммы и2(ж, у) = У2(ж,у) + П2(ж,у). Здесь Р2(ж,у) — решение задачи:

^2жж + У^2уу + P2V2y = 0;(11)

V2(0,y)=0, P2(Z,y)=0, -а^у^О;(12)

У2(ж, —а) = ф-а^, 0 С ж С Z,(13)

а П2(ж,у) — решение задачи:

и2жж — U^yy + p2U2y = 0;(11')

Z72(0,y) = р0(у),  U2(l,y) = Vi(y), -а^у^О;(12')

П2(ж,-а)=0.(13')

Решение задачи (8)—(10) будем искать в виде

У(ж,у) = Х(ж)У(у).(14)

Подставляя (14) в уравнение (8), получим два обыкновенных дифференциальных уравнения

У"(ж)+ ^У(ж) = 0, У"(у)-^У(у) =0,(15)

где k^ = -pi + кф Учитывая граничные условия (9), получим краевую задачу

^"(ж)+ ^Х(ж) = 0, X(0)=X(Z) = 0, решение которой имеет вид

Х(ж) = Х„(ж) = 8Ш^_1ПЖ, к_1п = ^ (п = 1,2...).

При k^_u = к^_п - pi общее решение второго уравнения (15) запишем в виде

^ы = у„(у) = с\п chk2n + С2п shfc2ny, где Cin,C2n — коэффициенты, подлежащие определению. Все функции

V1„(ж, у) = ^(ж)У„(у) = (Сщ с11/ь-2„у + С*2п sh к2пу)sinк1пх удовлетворяют уравнению (8) и граничным условиям (9) при любых постоянных Cin,C2n. В силу линейности и однородности уравнения (8), бесконечная сумма таких решений

У1(ж,у) = ^ [^in ^sh&2ny + Сф, shfc₂n(^ - у)]8т&1„ж             (16)

n = l также удовлетворяет уравнению (1) и граничным условиям ui(0,y) = ui(/,y) = 0,

У>°-                             , . , .

Рассмотрим теперь задачу (11), (12). С введением новых независимых переменных £ = ж, у = 2х/^У, уравнение (11) принимает вид

V2^ - V2t)T)--^---V2ll = 0.(17)

Это уравнение относится к классу уравнений Бесселя.

Из уравнения (17) после разделения переменных, с учетом граничных условий (12), получим

X"^EkU^ = 0, Х(0)=Х(0 = 0,(18)

У"(у) + ^^У'(у)+ ^У(у) = 0.(19)

Задача (18), как известно, имеет собственные значения к_4п и собственные функции Х_п^ = sin/гхпф Этим же собственным значениям соответствуют решения уравнения (19)

У» ГФ = ?/  ^2 [^Зп J1- р2 (^In^/) У ^4n Jp2 — 1 (^1п?/)] , где C3m,C4m — произвольные постоянные. Возвращаясь к переменным ж, у, решение У2(ж,у) уравнения (11) в области П2, обращающееся в нуль при ж = 0 и ж = I, запишется в виде

Уг(ж,у) = ^^ф^у)1 Р2 [C'snJi-p^fcinV^) + C4n-Jp2-i(fcinV^]sm^^ (20)

П = 1

Совокупность функций (16) и (20) представляет собой множество решений уравнения (1) в подобластях Qi и П2 соответственно, обращающееся в нуль при ж = 0 и

ж = I. Обозначим йфж, у) уравнения

Ml

(ж, у) = У (ж, у) + У2(ж,у). Рассмотрим задачу: , удовлетворяющее краевым условиям

найти решение

Ы1(ж,/l) = ^^(ж),  М1(ж, — а) = ф-_а(х),

причем ф_к (ж), ^-«(ж) еФфаД 'ф^Чо') = фЧ^ф = 0, и = 0,3. Имеет место

Утверждение 1. Пуств p-^p^cyh удовлетворяют условиям

Р1 7^ ^In ’ ^а 7^ (Ml+pa ’ ^т)/^^1и ’ th^n^ ф &2n/(l ^— Р2) ( \/ &1п ) ^Р2 •         (22)

Тогда задача (1), (21) всегда разрешима и притом единственным образом.

Здесь через ру^ди обозначены корни функции Бесселя первого рода порядка (1 ~ РзУ

• < Удовлетворяя й1(ж, у) условиям (6), (7), (21), относительно постоянных С^, j = 1,4 получим системы алгебраических уравнений для каждого фиксированного п

Г(2 - р) sh k_2uhC_2n - C_4n = О,

Г(2 - рфк_2и chk_2uhC_2u - (1 - р₂фVkinV”^p"C4n = 0, shk_2nhC_ln = ^_hn, (23) (2y/a)^{1 P2} Jl-p₂(ki_nV«)Ca_n + (2V«y ^P2 Jp₂-l(ki_nV“)C4_n = V’-an:

где i                                                                                          i

• ^h« = ^ j фь.^™к_1п^<1^ ф__аи = | У ^-«(^sinfcin^. о                                                о

Определитель А системы (23) имеет вид

А = Г(2 - p₂^2V^y-^p2JY-_PAkYu^

х [(1 - р₂ф VkYYY”^p" shk_2nh - k_2u chfc_2n/t] shk_2nh (24)

и отличен от нуля, если выполнены условия (22).

Итак, система (23) для произвольного натурального значения п всегда имеет решение и оно единственно. Решая систему (23), находим

О₂п — 0, ^4п — 0, С_1п — ф^/sh. k_2uh,

Сзп = Ф-ст/^Ф^1 P2Ji-p2(kln^a)].

Подставляя значения коэффициентов в (16), (20), получим их(ж,у) =

^1(ж,у)

^2 (ж, у)

= Е 'ФьпМ^-у^шк^х, п=1

= Е 'Ф-апМ_т^8шк_1пХ, п = 1

где

Обозначим и₂(ж, у) = Hi (ж, у) + И₂(ж, у), где Hi (ж, у) — решение задачи (8^,)-(10^/), a U₂(x,y) — решение задачи (П')-)^').

Относительно заданных функций у?о(у), У1Ы будем предполагать, что они кусочно-гладкие непрерывные функции на отрезке [-а,/г] и удовлетворяют условиям

^(-a) = T^W = ^W = О, ^ (-_а) = ^ (0) = ^ ^ = 0, и = М-

Предположим так же, что граничные функции у?о(у), Ti^ удовлетворяют условиям теоремы Гобсона [1], которая заключается в следующем:

Пусть /(д') — произвольная функция, определенная на промежутке [0, а) и удовлетворяет условиям:

• 1)    /(г) — кусочно-непрерывна и имеет ограниченную вариацию во всем открытом промежутке (0,а);

• 2)    интеграл

] z^f^dz о имеет конечное значение.

Тогда ряд Фурье — Бесселя

K^z) = ^2c_nJ_v (pvu-A (0 <  z < а)                   (27)

сходится и имеет своей суммой ^[/(г + 0) + / (г — 0)], т. е. представляет f^z^ во всякой точке непрерывности этой функции, где p_vu — положительные корни уравнения J_v(z') = 0, расположенные в порядке возрастания, а коэффициенты Фурье С_п определяются по формуле

1 Сп = „ т2 ,   . zKzpv \pVn ) dz, v^ ^   + 1 УЦУП ) J 0

(n= 1,2,...). ▻

Рассмотрим задачу: Найти решение н2(ж,у) уравнения (1), удовлетворяющее краевым условиям:

«2(0,у) = ТоЫ^ u₂(l,y) = уд(у), м₂(т, h) = м₂(т, -а) = 0.         (28)

Имеет место

Утверждение 2. Пусть pi,p₂,a,h удовлетворяют условиям pi ^ Ц, х/a ^ [/Цр₂-1,_т]/2тгп. Тогда задача (1), (28) разрешима и притом единственным образом.

• <    Согласно методу Фурье ищем частные решения уравнения (1) в виде

й2(ж,у) = Х(ж)У(у).                             (29)

Подставляя (29) в (1), получим уравнения (15), (19) относительно У(у), общие решения которых задаются формулами

У„ (у) = Ciscos 1/ Р! + k^y + C₂„sin Jр_х + к^у, у > 0,             (30)

Y_m^ = ^xF^\c\_mJi-_P2 (2V^) + C_2mJ_P2-i^V^^ У < о, (31)

где Cj_n, Cj_m (j = 1,2) — произвольные постоянные.

Функции Y_m^,Y_m^ вдоль прямой у = О должны удовлетворять условиям склеивания (6), (7) и однородным граничным условиям

CinCos ущ + k^h + C^sin урх + k^h = 0,                (32)

^F^"^P4Ci_mJi-p₂^V^^ + C_2mJ_p_^2V^^ = о.         (33)

Удовлетворив (30), (31) условиям (6), (7) получим соотношения, из которых непосредственно следует, что С_1п = С_1т = 0. Учитывая это обстоятельство, из (32) и (33) получаем равенства C^sin VPi + ^i^ ⁼ 0, С_2т J_P2-₇(2\fma) = 0. Выберем параметры ki,m таким образом, чтобы sin VPi + F¹ = °, J_P2-i(2Vma) = 0. Тогда собственные значения будут определяться равенством к^_п = (птг//г)² — щ, Хп = [Мр₂-1, ^п]/4а. Подстановка этих значений в уравнение X" =р ЦХ = 0 приводит нас к соотношениям

^п (*^) — ^Зп сЮщ/Ж + Ci^ бЬАц^Ж,

^„ (ж) = С5ПСО8%ПЖ + Сбп8ШХпЖ, где Cjn (д =3,6) — произвольные постоянные.

Таким образом, мы можем получить решение задачи (1), (28) в виде формальных функциональных рядов в Qi и Q2

ЕМ^ж,у) = ^(Fn dik_2in п=1

ж + С₈„ sh k_lnx sin —у, h

UFy^^UFF^F-i п=1

(Cg^cosx^a: + СюибтХпж), (35)

где Cj_m (д = 7,10) — произвольные постоянные.

Предположения, сделанные относительно граничных функций у0(у) и уд (у) при у < 0, позволяют представить их в виде рядов Фурье — Бесселя при помощи системы взвешенных бесселевых функций [1].

Определим теперь произвольные постоянные Cj_n (j = 7,10), входящие в (34), (35). Для этого представим граничные функции ipo^, фАу) ^ПР^И у < 0 в виде рядов Фурье — Бесселя по функциям

(    ?/) P^Jpl-l (^Рр2-1,п         ■

Будем иметь

РоЫ = ^^_0n(v^/Ty)¹"^P2^₂-i (/Д₂-1,™ п = 1                           '

^(у) = £ Wn(V-y)^{1 P2J}P2-i п = 1

^"М а

где коэффициенты Фурье — Бесселя вычисляются по известным формулам [2, 3]

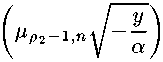
Й,

^°" = о 72 (и---Т [ ^Ш^У""1^-! р2\Рр2-1,п) J и- = «д (/.,.-,,„) / ^mv^tX-v (f«-L« ф5)*    1371

Удовлетворяя (34), (35) неоднородным граничным условиям (28), получим

{ [7_х(ж,у) = Ё (^o„chfci„2: + ^_nshfci_n2:)sin^y,

77 = 1

ОО

П₂(ж,у) = Ё (V-у) ^P2jp^-i У-р^.-Х V4) ^oncosxnx ф^зт/с^ж), n = l

₌

lu

- ^_Ои ch^iJ shk_lnl

I 2 Г . П7г

-  y₀(y)sin — ydy,

Уп - VOnCOSXnl hJ h_y, rm s.nxJ , 0

VomVin определяются формулами (36), (37) соответственно. >

Полученное формальное решение м(ж,у) = й1(ж,у) + й₂(ж, у) задачи (1)-(7) при наших предположениях относительно граничных функций ф-а^х^фь^^окУ^^АУ^ является регулярным. Справедливость этого факта при у > 0 устанавливается с помощью общей теории рядов Фурье [2], а при у < 0 опираясь на результаты, полученные ^в [4].                                                     _

Пусть теперь рх = р₃ = О, /₀ = 0, р₂ = -2т/, и > 0, т = 0.

Решение задачи (1)-(7) снова будем искать в виде суммы двух функций м(ж,у) = Mi (ж, у) + и₂ (ж, у), где в свою очередь функция их (ж, у) ищется в виде суммы их (ж, у) = У1(ж,у) + Hi (ж, у), причем Р1(ж,у) является решением уравнения (8) и удовлетворяет граничным условиям

7?1П1(0,у) = T?2P1(Z,y) =0,(38)

ДзУ^ж,/!) = ^(ж),(39)

а Их (ж, у) — решение уравнения (8'), удовлетворяющее граничным условиям

Д1И1(0,у) = у)0(уф R2U^l,y) = ^(у),(40)

ДзП^ж, /1) = 0.

Функция н₂^х, у) ищется в виде суммы н₂^х, у) = V₂^x, у) + U₂(x, у), где V₂^x, у) — решение уравнения

V2M - V2yy - ^vV^y = 0,(42)

удовлетворяющее граничным условиям

Д1У2(0,у)=0, Д2У2(/,у)=0, У^-оф = ф_а^,(43)

а П2(ж,у) — решение уравнения

П2и - U2yy - ‘IvU^ = 0,(43')

удовлетворяющее граничным условиям

RiU2(0,y) = УоСу), Н2и2(1,у) = узфуф(44)

П2(ж,-а) = 0.(45)

Положим У1(ж, у) = Х(ж)У(у). Тогда из уравнения (8) и граничных условий (38) относительно У (ж) будем иметь задачу Штурма — Лиувилля

Х" + АХ = 0, адА^О) - ДХ(0) = 0, а2Х'^ + 32Х^ = 0,(46)

а относительно Y (у) получаем уравнение

Y" - АУ = 0.(47)

Собственные функции задачи (46) имеют вид

Ап(ж) = a„sin х/Х^х + 6„cos х/Х^х, где                         __________ __________ а» = А У ^Хпа^ + 31, bn = («1 уА») У УА„«1 + 31-.

а А„ — корни уравнения (ai«2A - /3i/32)tg\/A/ = \/A(ai/32 + /31 a2), причем и              f v2( i , I (/3i«2 +/32ai)(Ana?ia2 +/3i/32)

||X„_W|| =]x„_Wdx=-₊ ^-^^-^ .

При A = A„ общее решение уравнения (47) запишем в виде

^(у) = Yn^ = C1„ sh V^y + с_2п sh(/i - у).                (48)

Тогда

^1(ж,у) = ^2 (cinsh х/Х^у + c_2nshx/)^(h - у))Х_п(х).            (49)

П = 1

Решение задачи (8'), (40) будем искать в виде суммы Uy^x,y) = г/(ж,у) + гс(ж,у), где функция щ(ж,у) подбирается так, чтобы она удовлетворяла только граничным условиям (40). Ищем м(ж,у) в виде го = ку + к₂х и подбираем константы ку и к₂ так, чтобы выполнялись условия (40). Это дает систему двух алгебраических уравнений, решая которую находим ку. Окончательно получаем

™(ж,у) = {(а2 + М^ - ^WoV^ - («1 + P^WM^X, где

А = ~(ац/Зг + /31«2 + P1P2IV

Подставляя Их (ж,у) в уравнение (8) и краевые условия (40), (41), получим условия для определения урс,уУ z^ + vyy = 0,(50)

Ryv(0,y) = 0, Д2^,у) = 0,(51)

R3v(x,h) = 'фн^У(52)

где

'^(ж) = - —!—{а₃[(а₂ + ^₂(1 - ^xWoW - (оц + руХ^^КУ

+ ЗЫ(«2 + АИ^ - x^cp₀W - («1 + руХ^фНуУ

Решение задачи (50)—(52) будем искать в виде

Ц^тр = ^XnX_n(chV^y + y_nshVx^y)₁ Уп = Ps/P^VM- (53)

Здесь Х„(ж) — собственные функции, а А„ — собственные значения краевой задачи (40).

Удовлетворяя (53) краевому условию (52), получим фк^ = Vxn 5 2— ch VKh+ —7„ +    sh\/XJiA ХДхф

_. V “з             \«з           /          J

Следовательно,

= ( [ M)Xn^dA/ U—^V^hE

U             J I «з

о

—7n +

«3

v^shvx;^} j а^ю^. о

Таким образом, решение задачи (8)-(40), (41) имеет вид

^1(ж, у) = 52 Хп (ch Vx^y + 7„ sh vX^y) А„(ж) n = l

+ [(«2 + P2P - ж))^о(у) - («1 + руХ>фу^/Х.

Собственные функции Ап(ж) и собственные значения А„ задачи (42), (43) снова определяются из краевой задачи (40).

Для определения Упфф получим дифференциальное уравнение у"^ + 2ру;^ + хпуп^ = о.(55)

Общее решение уравнения (55) имеет вид [5]

УДу) = (сзп chw„y + c4n shw„y)e"l,y, wn = V^2 - Ч, Д > Хн .(56)

УДу) = (c3ncoswny + c4nsinwny)e-1/y, wn = VXn- v2, v2 < A„,(57)

У»(у) = (сзп + c4uy^e"vy, V2 = A„.(58)

Решение краевой задачи (42)-(43) имеет вид

^2 (ж, у) = ^УДу^ХДхф(59)

п = 1

где УДу^ соответствует одному из представлений (56)-(58).

Решение задачи (43')-(45) имеет такой же вид, что и ПДх, у), только h и —а нужно поменять ролями. Следовательно, в этом случае мы имеем решение в виде

ПэД^ = ^x_n(ch V>^y + 7„ sh VKy)X_n^ n = l

+ [(«2 + ^2(^ - ж))у?о(у) - («1 + /34ж)^(у)]/А, где

Хп

Уф ДД)ХДМ

2^ ch аз

ДДД -

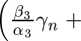
ДД Silvia

j X²^ d^ о

Ф-ДД = ?ДтД 2—ch yA_na - —7„ + V^n sh у A_na >Х_п(ж). __Л ( «з             \a₃          )         J

Удовлетворяя и(ж,у) = и₄(ж,у) + и₂(ж,у) граничным условиям (21) и условиям сопряжения и⁺(ж,0) = и^-(ж,0), Uy (ж,0) = и“(ж,0), получим систему линейных алгебраических уравнений относительно c_in, г = 1Д, которая однозначно разрешима, если определитель этой системы

А = sh VKh (z/ • sh VKh • sh w_na - VK • ch VKh • sh w_na

- w_n • chw„a • sh VKh) ^ 0.

В силу условий, наложенных на заданные функции 2₀(у), (fi(y), 'фь (ж), 'ф-_а (ж), можем заключить, что функция и(ж,у) = и₄(ж,у) + иг(ж,у) и ее частные производные до второго порядка включительно непрерывны в областях Qi и Q₂, что означает равномерную сходимость как и₄(ж,у) и и₂(ж,у), так и рядов полученных от них путем дифференцирования до второго порядка.

Задача (А) при /о ^ 0, р^ ^ О, рз ^ О, т ^ О решается аналогично предыдущему случаю.