О некоторых методах определения длины трансплантата периферических нервов, кровеносных сосудов и сухожилий

Травма предплечья и кисти является самой частой среди всех травм конечностей, полученных в мирное и военное время. По данным авторов, частота таких повреждений варьируется от 30 до 57 % [4, 5, 7]. В последние годы наблюдается существенный рост тяжелых травм конечностей, среди которых травмы верхних

• © Баранов Н.А., Кабанов С.Н., Масляков В.В., 2015

Баранов Николай Алексеевич, ассистент кафедры клинической медицины, Саратов

Масляков Владимир Владимирович, д.м.н., профессор, проректор по научной работе и связям с общественностью, заведующий кафедрой клинической медицины, Саратов конечностей (88 %) превалируют над травмами нижних (12 %) и занимают ведущее место среди травм опорно-двигательного аппарата (до 70 %) [1].

В то же время неудовлетворительные результаты лечения таких больных составляют 20–40 % [3, 4, 13]. В специализированных отделениях хирургии кисти больные с последствиями повреждений кисти и предплечья составляют 40–56 % [8].

Последствиями травм кисти и предплечья с повреждением сухожилий и нервов являются сгибательные и разгибательные контрактуры пальцев, отсутствие той или иной функции пальцев и кисти, глубокие и необратимые трофические нарушения.

Развитие микрохирургии существенно поменяло ситуацию, за короткое время был пересмотрен подход к лечению больных с представлявшимися прежде нетяжелыми травмами. Количество операций, выполненных на нервах и сухожилиях, непрерывно растет. Между тем даже после широкого внедрения в медицинскую практику высокотехнологичных операций число неудовлетворительных исходов лечения больных с травмой кисти и предплечья остается достаточно высоким.

Математическое моделирование некоторых типичных хирургических ситуаций, выполненное в данной работе, по существу вызвано следующими соображениями. Как видно из работ [2, 6, 9–12, 14, 15], до недавнего времени существовал значительный разброс данных при определении некоторых параметров хирургических вмешательств. Так, например, размер диастаза (от греч. diastasis – разделение, промежуток; термин, принятый в микрохирургии для обозначения величины расхождения концов поврежденной структуры) в случае травмы нерва, при котором разные авторы считали необходимым использование трансплантата, варьировался от 1 до 7 см.

Подобные подходы свидетельствуют о произвольности выбора размера, тогда как оптимальный размер трансплантата, а также сам вопрос о его фактической необходимости определяются не только практическим опытом хирурга, но и рядом объективных показателей, к которым мы относим, в первую очередь, силу натяжения неповрежденной эластичной структуры.

Авторы сочли возможным выделить в отдельную самостоятельную группу часть оперируемых структур, а именно, сосуды, нервы и сухожилия (в последнем случае имея в виду мышцу с сухожилием, которую в дальнейшем будем именовать сухожилием).

Данные структуры обладают сходными физическими свойствами: протяженностью (т.е. преобладанием одного из измерений над остальными); эластичностью, характеризуемой сходными прочностными характеристиками; сосуды, нервы и сухожилия находятся в нормальном (неразрушенном) состоянии под воздействием определенной силы натяжения, специфической для каждой из структур. Именно поэтому мы объединили данный класс оперируемых структур термином эластичные структуры.

Разумеется, мы не могли охватить все многообразие микрохирургических операций и рассмотрели наиболее типичные случаи повреждения эластичных структур на предплечье и кисти.

Математическая сложность поставленной задачи определялась, прежде всего, отсутствием данных для проведения необходимых расчетов. В ходе исследования авторам удалось предложить малотравматичный и эффективный способ преодоления указанной неопределенности.

Цель исследования

Цель – математическими методами определить оптимальную в определенном смысле длину трансплантата при восстановительных микрохирургических операциях на эластичных структурах: нервах, кровеносных сосудах и сухожильно-мышечных комплексах.

Материалы и методы

Экспериментальные исследования проведены на двадцати невскрытых трупах мужского пола в возрасте от 20 до 49 лет не позднее суток после смерти; причина смерти во всех случаях не была связана с травмой конечностей. Результаты замеров были использованы для выяснения общности оперируемых биомеханических структур и проверки эффективности полученных математических формул.

Результаты исследований были использованы во время операций реплантации крупных сегментов конечностей у 153 пациентов и в некоторых других микрохирургических вмешательствах. Это позволило уменьшить количество неудовлетворительных исходов при выполнении восстановительных операций.

Для реализации математических методов определения по двум замерам силы натяжения, определения длины трансплантата, а также определения силы натяжения при восстановлении эластичных структур создана программа TIN ( Tension Interface ). Она позволяет определять силу натяжения эластичной структуры и площадь ее поперечного сечения с тем, чтобы вычислять силу натяжения, отнесенную к единице площади, а также определять величину трансплантата и силу натяжения восстанавливаемой эластичной структуры. По заданному значению модельной силы натяжения и силе натяжения, определяемой специальным измерением, для одного из концов восстанавливаемой эластичной структуры указанная программа позволяет определять значение силы натяжения другого конца эластичной структуры таким образом, чтобы при восстановлении эластичной структуры сила натяжения ее совпала со значением модельной силы. Для выполнения этих функций производились соответствующие измерения, и результаты этих измерений вводились в соответствующие поля формы программы, которые описывают параметры объекта манипуляций и операционного поля.

На рис. 1 представлена распечатка экрана пользовательского интерфейса программы TIN в типичном случае. Программа TIN использует специальную систему управления базой данных Paradox 7.0.

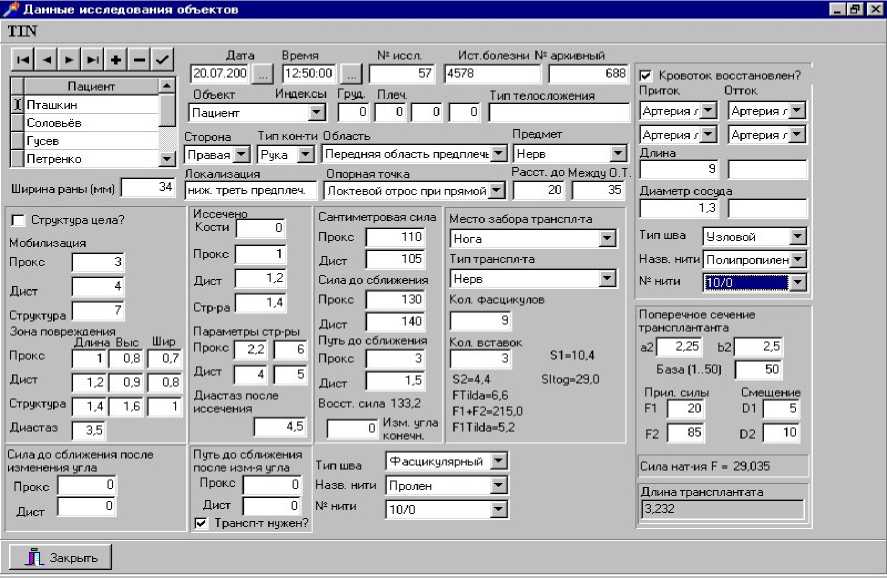
Рис. 1. Распечатка экрана пользовательского интерфейса программы TIN в типичном случае

Для корректной работы приложения на компьютере пользователя должна быть установлена система, поддерживающая интерфей с к этой базе данных Borland Data Base Engine . Приложение выполняется на компьютере с установленной операционной системой Windows 9 X , Windows NT 4, Windows 2000. Требования к оперативной памяти, размеру необходимого свободного дискового пространства определяются необходимыми ресурсами для операционной системы и системы уп р авления базой данных (32 Мб оперативной памяти, 15 Мб свободного дискового пространства).

Одной из основных трудностей при с оздании математической модели конкретной эластичной структуры была ее пространственная сложн о сть: артерии и нервы характеризуются значительной разветвленностью. Но типичной при выполнении хирургического вмешательства является работа с линейным участком мобилизов а нной эластичной структуры. Поэтому с достаточной сте п енью точности мы можем считать, что силы натяжения, распределенные вдоль коллатералей, заменены их равнодействующей вдоль линейного участка. При этом для практи ч еских формул оказалось неважным конкретное место приложени я равнодействующей силы. По сути дела, мы не знаем истинного размера эластичной структуры, участвующей в моделировании, но, как оказалось, это и не является необходимым. В случае рассмотрения ситуаций с сухожилиями мы имели в виду весь сухожильно-мыше ч ный комплекс, который, очевидно, обладает эластичными свойствами, и, разумеется, к сухожильно-мышечному комплексу применимы, с незначительными м одификац и ями, все рассуждения, приведенные для сосудов и нерво в .

Сила натяжения при проведении микрохирургических о пераций уже достаточно давно была предметом внимания многи х ведущих хирургов мира.

По результатам наших исследований был создан прибор для практического определения по двум замерам силы натяжения эластичной структуры. Н иже приведены необходимые построения и выводы.

Определение по двум замерам силы натяжения эластичной структуры

При определении продольной силы натяжения в растянутых эластичных структурах посредством приложения поперечной силы и вызываемого ею прогиба и определении по значениям измеренных величи н силы натяжения п редварительно жестко закрепляют две точки A и B эластичной структуры, между которыми проводят измерения с тем, чтобы исключить возможн ы е смещения в местах опорного закрепления структуры (рис. 2). Измеряют расстояние между точками A и B . В средней

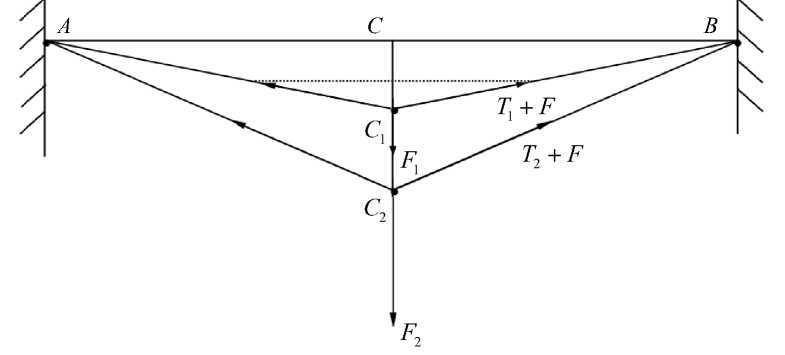
Рис. 2. Определение продольной силы натяжения неразрушенной структуры точке С перпендикулярно структуре прикладывают силу, которая смещает ее на величину d1 , и измеряют величину этой силы F1 . Эксперимент повторяют. К средней точке С перпендикулярно структуре прикладывают силу, которая смещает ее на величину d2 относительно первоначального положения, и измеряют величину этой силы F2 .

Силу натяжения, действующую между зафиксированными точками A и B в точке С , определяют по приведенной ниже формуле (9). При решении данной проблемы используется закон Гука в следующей форме:

T = ES 8, где Е – модуль Юнга эластичной структуры; S – площадь поперечного сечения эластичной структуры; 8 - величина деформации эластичной структуры.

Обозначим искомую силу натяжения F . Тогда при первом нагружении сила T ₁ определяется по формуле

T 1 = ES 8 1 ,                                             (1)

J d? + x2 - x где 81 =  ---------, а x - половина расстояния между точками A и B.

x

В самом деле, рассмотрим треугольник СС ₁ В . В результате приложения в точке С силы F ₁ отрезок СВ эластичной структуры длины х трансформируется в отрезок С ₁ В , при этом его длина увеличится. Длину отрезка С ₁ В легко найти с помощью теоремы Пифагора из треугольника СС ₁ В . Квадрат длины отрезка С ₁ В как гипотенузы рассматриваемого треугольника равен сумме длин квадратов катетов, которая в нашем случае равна d 1 ² + x ² . При этом величина ^d ^ + x ² - x показывает, насколько удлинился отрезок CB , или величину его абсолютного удлинения. Деля величину абсолютного удлинения на исходную длину отрезка, приходим к формуле для 8 1 .

При втором нагружении сила T ₂ определяется аналогично, только теорема Пифагора теперь применяется к треугольнику CC 2 B. Поэтому

T2 = ES 82,(2)

л / d 2 I x x где 82 =  

x

Таким образом, мы получаем условие равновесия для узла С в следующем виде:

Fi= 2(T + F) -/==.(3)

d 1 ² + x

Так как сумма всех действующих в точке С ₁ сил должна быть равна нулю, то приложенная при первом нагружении сила F₁ компенсируется суммой двух сил T₁ + F , действующих вдоль линий АС ₁ , ВС ₁ . Для получения численного соотношения (3), связывающего рассматриваемые силы, рассмотрим треугольник СС ₁ В . Сила, компенсирующая силу F ₁ , действует в противоположном ей направлении от С ₁ к С . Скалярные значения величин F₁ и 2 ( T + F ) связаны следующим соотношением:

F 1

2( T + F )

= cos Z CC₁B .

Косинус угла СС ₁ В легко определяется из треугольника СС ₁ В . Так как длина

СС1 = d 1, а длина С1 В = dd 2 + x2 , то отсюда получаем cos Z CC1 B =

d ₁

d ² + x²

При втором нагружении условие равновесия записывается в форме

F 2 = 2'! + F )     d ²    .                                 (4)

Ц d ₂ ² + x

Далее, из формул (1) и (2) следует t = 7 d 2+x2 - x                                (5)

T2" d ₂ ² + x² - x ’

Из формулы (5) получаем выражение T ₂ через T ₁

,     '^ d 2 I x x ,

7 d 2 + x ² — x

Теперь в группе уравнений (3), (4) присутствуют только две неизвестные величины F и T ₁ , подставляя выражение для T ₂ из (6) в (4), получаем

T1 + F =

¹7 d i ⁺ x г?

^F 1 ^,

2 d ₁

yjd 2 + x — x dci + + x — x

T1 + F =

1 7 d 1 + x²

2     d ₂

Исключая в системе (7) T1 , находим искомую силу натяжения F . С этой целью d + x — x умножим обе части первого уравнения системы на величину 2        и вычтем из d 1 + x2 — x полученного второе уравнение системы (7). В результате получим

F

aJ d 2 + x² 7 d 12 + x x

7d 22 + x2

x

- F ■ F =

x

■ 7 d 2 + x x

л! d- 1 I x x

1 a] d 12 + x ² A^ d 2 + x x 2- ~~di /1 ² + x²

1 ^ d 1 + x x aJ d 22 +;

= 2 ”^1   dj2+T:

x

F 1 x

■ 2 s

s

1d22

x

- F1 s

x

d 2

1 d22+

2 d ₂

F 2 .

2F2.

F =

1 a] d 1 + x ² a] d 2 + x x

2      dj^+x^

F -

— x

1 a] ^d 2 ^{+ x}

F 2 d ₂ ²

a^ d 1 + x — x

a] d 2 + x ² s ^ d 1 + x x

1 7 d 2 + x x

7 d 2 + x ²

s

x

2    d 1    dd xx

s

^d 2 + x x

F "

1 7 d 2 + x²

a] d 1 + x² s x

2   d 2    ^ d 2 + x2 s 7 d 12 + x2

F2.

Теперь оба слагаемых в правой части полученной формулы умножим и разделим на

кроме этого , первое слагаемое умножим и разделим на

, а второе на

соответственно. Эти преобразования позволяют получить представление для искомой силы в форме, значительно уменьшающей вычислительную погрешность. В результате после очевидных упрощений получим

F =

2( d 2 s d 2 ) ^ d ₁

x + 7 d2 + x2

x2

—F s

d2

x +

2 x

A

^F 2 -

Или в форме , более удобной для вычислений :

F =

+ x ² + d d 2 2( d 22 s d 2 )

^d 2 ²

F " d ²

x2

F

.

Применение формулы (9) предпочтительнее в сравнении с формулой (8), так как снижается вычислительная погрешность .

Определение величины трансплантата

Математическая модель задачи определения величины трансплантата может быть представлена следующим образом. Пусть задан отрезок растянутой эластичной структуры с поперечным сечением S и длиной l . В ненатянутом состоянии длина структуры

–

l₀ . Обозначим

Возникающую при этом силу следующего соотношения :

концы растянутой эластичной структуры А и В. натяжения F можно определить по закону Гука из

F = ES ( l s l o )

^l 0          ^,

A

l

B

l 0

Рис. 3. Схема длин структуры

Рис. 4. Схема длин отрезков где E – модуль Юнга исследуемой эластичной структуры. Схематически это может быть представлено на рис. 3.

Затем из внутренней части растянутой эластичной структуры AB удаляется отрезок некоторой фиксированной длины A'B' , при этом оставшиеся отрезки структуры AA' и B'B переходят в свободное, ненатянутое состояние AA" и B"B . Удаленный отрезок эластичной структуры также переходит в свободное, ненатянутое состояние A ''' B ''' (рис. 4).

Длину отрезка A ''' B ''' обозначим l _иск , она и подлежит определению. Математическая сложность данной задачи выражается в том, что l ₀ , l , E , F неизвестны.

Обозначим через d длину отрезка A"B" . Физически этот отрезок представляет собой величину диастаза. Сумму длин отрезков AA" и B"B обозначим l ₀ ' , тогда

d + l 0 = l .

С другой стороны , очевидно , что для l _иск справедлива следующая формула :

¹ иск ^{+ 1} 0      ¹ 0 •

Физически это означает, что к оставшейся после удаления отрезка A'B' длине l0 нужно добавить длину отрезка A"'B” для того, чтобы вернуть систему в первоначальное ненапряженное состояние. Вычитая из соотношения (11) соотношение (12), получим

^d - ¹ иск = ¹ - ¹ о •

Умножим обе части полученного соотношение (13) на , тогда получим l 0

^ ( d - l иск ) = ES ( l - l о ). l ₀ l ₀

В соотношении (14) правая часть – это сила натяжения из формулы (10). Таким образом, из (14) и (10) получаем

'е = d — — иск

ES

.

ES

Представим величину Д =-- следующим образом:

l 0

F = ES ( l о + 1 - l 0 )

¹                l 0

.

Тогда эта величина может быть истолкована как величина силы натяжения, возникающая при растяжении первоначально нерастянутой эластичной структуры длиной l ₀ на единицу длины.

Из формулы (15) видно, что для определения величины вставки l _иск нам необходимо знать величину диастаза, величину силы натяжения эластичной структуры F , а также величину силы F ₁ . Величина диастаза может быть измерена непосредственно. Для определения силы F с достаточной степенью точности можно использовать процедуру замера этой силы по методу, изложенному в предыдущем пункте (см. формулу (9)). При этом лучше всего замерять эту силу на сходных с восстанавливаемой структурах. Если вставка делается из структуры другого поперечного сечения, то разумно перейти к единым силам натяжения, а именно к силе, отнесенной к площади сечения. Подобный переход как бы трансформирует нашу задачу в задачу для структур единого сечения. Для определения площади поперечного сечения восстанавливаемой и трансплантируемой структур можно приближенно считать, что сечение этих структур имеет форму эллипса, так что

S 1 = п ab, (17)

где a , b – полуоси эллипса.

Для определения силы F1 вначале сделаем следующие преобразования. Введем в рассмотрение силу F2 по формуле

F 2 =

ES ( 1 ₀/2 + 1 - 1 ₀/2)

l 0 /2

Эта сила характеризует усилие, которое необходимо приложить к отрезку нерастянутой эластичной структуры половинной длины l ₀ /2 , для того чтобы растянуть его на единицу длины. Согласно (16) и (18) для сил F ₁ и F ₂ выполняется соотношение

F 2

.

На практике для определения силы F2 нужно проксимальный конец восстанавливаемой структуры оттянуть на единицу длины от исходного положения и замерить требуемую для этого силу. При относительно небольших величинах диастаза можно приближенно считать, что величины отрезков AA" и B"B равны 20 , и, следовательно, приближенное значение искомой силы F1 можно определить из формулы (19). Таким образом, формула (15) может быть записана в виде l = d- —

иск F и использована для нахождения приближенного значения lиск при условии, что мы тем или иным способом сумеем найти приближенное значение силы F1 .

Другой способ определения силы F ₁ , отличный от формулы (19), будет предложен ниже. При этом будут использованы измерения сил при удлинении проксимального и дистального концов на 0,5 см, что в сумме дает 1 см. Там же будет дан комментарий о математической природе данного подхода.

Проанализируем формулу (20). Значения правой части формулы (20), формально говоря, могут быть как положительными, так и отрицательными, а также равными нулю. Рассмотрим случай равенства нулю. Это значит, что для восстановления состояния необходимо просто соединить концы A" и B" . Физически это означает, что мы имеем дело со свежим порезом, без атрофии концов соединяемой ткани. В случае отрицательных значений правой части формулы (20) физически это означает укорочение конечности – дело может быть сведено к нулевому значению диастаза в формуле (20), а получаемое при этом отрицательное значение вставки означает, на сколько суммарно нужно укоротить дистальный и проксимальный концы.

Определение силы натяжения в восстанавливаемой структуре

Математическая постановка задачи определения силы натяжения в восстанавливаемой структуре может быть описана следующим образом.

Задан отрезок АВ поврежденной эластичной структуры таким образом, что содержательно он состоит из двух отрезков АА' и В'B длин l ₀ ' и l ₀ '' соответственно (рис. 5). Величина диастаза, т.е. длина отрезка А'B' , равна d . Эластичная структура восстанавливается путем растягивания и соединения отрезков АА' и В'B в некоторой точке внутри отрезка А'B' , помеченной на чертеже вертикальной чертой. При этом известны силы натяжения F ₁ , растягивающая отрезок АА' , и F ₂ , растягивающая отрезок

В'B. Мы дадим два решения этой задачи: вначале для случая одинаковых эластичных свойств отрезков АА' и В'B, а затем для случая различных эластичных свойств рассматриваемых отрезков.

1-й случай . Как хорошо известно, сила натяжения F 1 определяется по закону Гука следующим образом:

_ SE а d

F                   ■ где S – площадь поперечного сечения эластичной структуры; Е – модуль Юнга эластичной структуры; а - некоторое число между 0 и 1, определяющее положение точки соединения отрезков ЛА* и ВB внутри отрезка А'В'. Например, если а = 0,5, то вертикальная черта, т.е. точка соединения, находится посередине отрезка А'В'.

А                        А'    B'               B d I"

Рис. 5. Схема поврежденной эластичной структуры

Аналогично для силы F 2 получаем выражение

F 2 =

SE (1 -a ) d

I"

Подсчитаем теперь силу натяжения, которая возникает при соединении отрезков АА' и В'B . Суммарная длина нерастянутой эластичной структуры в этом случае равна l ₀ ' + l ₀ '' , после растяжения длина эластичной структуры становится равной l ₀ ' + l ₀ '' + d . Тогда значение искомой силы F определяется следующим образом:

SEd

.

1 0 + o_o

Преобразуем правую часть полученной формулы следующим тождественным образом:

SEd

Г

1 0 + 1₀

f SE a d Y SE (1 -a ) d )

V 1 о JV     1 о

SE a d_z1   , SE (1 -a ) d

----(1 - a) + — — a

ГГ’

А теперь, вспоминая представления (21) и (22) для сил F ₁ и F ₂ , получаем

SE a d

V l o '

Y SE (1 -a ) d )

7 V 'o 7

F 1 F 2

SE a d _n        SE (1 -a ) d     (1 -a ) F1 + a F ₂ ’

vA- I                                    VA/

Г              Г'

или окончательно

F =___ FF___ (1 - a ) F + a F 2

.

2-й случай . В этом случае будем пользоваться нашим чертежом, только будем считать, что характеристиками отрезка АА' и В'B являются S ₁ E ₁ и S ₂ E ₂ соответственно. Тогда, по аналогии с первым случаем, сила F ₁ определится следующим образом:

S,E, a d

F Г а сила F2 из соотношения

F 2 =

S 2 E 2 (1 -a ) d

I”

l ₀

При соединении отрезков АА' и В'B в точке, помеченной вертикальной чертой, эта точка сместится на величину х , вообще говоря, неравенства сил F 1 и F 2 . Возникшие при этом силы F ₁ и F ₂ будут равны, и для них будут справедливы следующие представления:

~   S₁ E₁( a d + x )

^F 1 = —Г---’

F 2 =

S 2 E ₂((1 -a ) d - x )

I"

Условие равновесного состояния восстановленной эластичной структуры выразится как F₁ = F 2 или

SE Ca d + x ) _ S 2 E ₂((1 -a ) d - x ) 1'       = p

Решая уравнение (28) относительно х , последовательно получаем

S ₁ E ₁ a d

+

S ₁ E ₁ x  S ₂ E ₂ (1 - a ) d  S ₂ E ₂ x

или, вспоминая формулы (21) и (22) для F 1 и F 2 и перенося слагаемые с х в правую сторону, имеем

S₁E ₁ S ₂ E ₂

V 'о ‘0 /

В формуле (29) умножим и разделим первое и второе слагаемые в скобках в правой части на a d и (1 -a ) d соответственно. Тогда с использованием (21) и (22) получим

F2 - F =

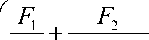
_Va d (1 -a ) d _v

Решая формулу (30) относительно х , получаем

( F ₂ - F ) a d (1 -a ) F (1 - a ) + F ₂ d

Так как значение силы натяжения F , возникшей при восстановлении эластичной структуры, равно значению любой из сил F ₁ или F ₂ , то ее значение определится по любой из формул (26) или (27). Возьмем, например, формулу (27), тогда получим

_ ~ SE ( a d + x ) SE a d S,E,x a d  _ F

F = F ₁ =    --------=+ ^{1 1} .--- = F ₁ +—- x .

1 ₀'               1 ₀'          1 ₀'     a d a d

Подставляя в последнее представление для F в формулу для х (31), окончательно получаем

F =--- FF ---, (1 - a ) F + a F ₂

что в точности совпало с формулой (23). Таким образом, значение возникающей при восстановлении эластичной структуры силы натяжения F не зависит от эластичных свойств соединяемых концов. Формула (32) может быть использована, например, следующим образом. Пусть задана эталонная сила натяжения F, которая должна возникнуть после восстановления разрушенной эластичной структуры, и пусть мы сами выбрали значение одной из сил натяжения F1 или F2 , для определенности мы замеряем силу F1 . Тогда в формуле (32) нам известны F и F1 . Решая уравнение (32) относительно F2 , получаем

F2 = (1 - a)

FF 1

F1 -aF

Таким образом, зная численное значение правой части полученной формулы, мы можем укорочением или удлинением второго отрезка подобрать значение интересующей нас силы F ₂ таким образом, что возникающая при восстановлении эластичной структуры сила численно равна F. Этот способ может быть использован, например, при определении величины трансплантата.

Второй способ определения величины трансплантата

Еще один способ определения величины трансплантата состоит в изменении метода, предложенного выше. Суть метода – в модификации формулы (20), а именно: для определения силы F ₁ в формуле (20) может быть предложена другая процедура. Для определения F ₁ оттянем дистальный и проксимальный концы восстанавливаемой структуры на 0,5 см каждый. Тогда, как следует из результатов данного раздела, для F ₁ может быть применена следующая формула:

F i =

2 FF dp

Fa + F dp где Fd и Fp обозначают дистальную и проксимальную силы соответственно при удлинении отрезков восстанавливаемой эластичной структуры на 0,5 см. Более того, нами установлен следующий факт. Введем в рассмотрение последовательные приближения для определения искомой величины трансплантата по следующей формуле:

1 k+1 = dF-----, иск        SE (l0 + l0 + lИск)

где 1 ₀’ , 1 0 - длины отрезков AA", B"B соответственно. При этом lim l k^ = l _иск и l ⁰ _c = 0. k ^^               ^{и K}

С этой точки зрения формула (15) при выбранном согласно (34) значении F ₁ представляет собой начальное приближение l _и ¹ _ск . Нами предложена эффективная процедура подсчета величины знаменателя в формуле (35) для первых итераций, а практическое применение формул (15) и (34) дало отличный результат.

Покажем, что формула (35) действительно определяет сходящуюся к точному решению l _иск последовательность приближений. С этой целью перепишем формулу (35)

в следующем виде:

lk+1 = d - F- (l' +10 + lk ) = d - SE(l -lo) (l' +10 + lk ) = иск     SE 00 иск        SEl 00 иск ll0        k d ,    (10 + 10 + l иск ), l0

или

/^k - C + ¹—⁰l^k ,                              (36)

иск                   иск , l0

где

C = d -——0 (1‘ +1").

l ₀

Формула (36) представляет собой итерационный процесс со «сжимающим

• ¹    - l o

оператором» в том случае, если величина    0 меньше единицы. Это выполняется при l0

I <  2 I ₀ , что, очевидно, всегда имеет место для трансплантируемых тканей (величина растянутой эластичной структуры не должна превышать двух длин нерастянутой структуры). Отсюда следует, что итерационный процесс (35)–(36) сходится к некоторой величине 1 И _ск . Покажем, что 1 И _ск = 1 _иск . В самом деле, переходя к пределу в обеих частях формулы (36), получаем

* ^ll 0          *

• ¹    иск ^И , V0 ⁺ ‘0 ⁺ ‘иск ) •

l ₀

Отсюда получаем представление для l_и ^* _ск :

* ddl^ _ I ^- 1 ⁰

• ¹    иск       1         1 V ¹ 0 ^{+ 1} 0 )•

Далее, Вспоминая, ^что 1 0 ' + 1 0 '' = 1 0 - 1 иск , 1 иск = d - 1 + 1 0 , Получаем 1 и*ск = 1 иск •

Формула (34) для определения F ₁ из данного раздела представляет собой другой способ определения начального приближения силы F ₁ из формулы (16).

Влияние полученных результатов на алгоритм действий микрохирурга

Математическое моделирование, использованное при решении этой задачи, потребовало определенной перемены логики выполнения операции. Это вызвано необходимостью проведения некоторых ранее не выполнявшихся замеров и определенных компьютерных вычислений, результаты которых использовались при определении длины трансплантата и ряда других характеристик восстанавливаемых эластичных структур. Из полученных формул и хирургической практики следует, что при проведении операций по укорочению конечностей иногда необходимо резецировать концы костей и эластичных структур. Успех проведенных восстановительных операций обусловлен также организационными и хирургическими действиями: оперирование двумя бригадами хирургов с целью сокращения сроков включения отсеченного сегмента в кровоток; проведение «провизорного остеосинтеза» с заменой его в раннем послеоперационном периоде или в конце операции на окончательный вариант остеосинтеза, чаще всего аппаратный. Промывание кровью больного во время включения в кровоток отсеченного сегмента позволило избежать «синдрома включения». Большой психологический эффект имела также ранняя психофизиологическая реабилитация. При выполнении операций использовались микроскопы OPMI 7 D , OPMI Pentero , укомплектованные флуоресцентной диагностической системой Multivision и операционным CO ₂ -лазером. Отдаленные результаты изучены у 131 пациента: 19 отличных, 77 хороших (больные вернулись к прежней трудовой деятельности), 35 неудовлетворительных.

Заключение

Полученные результаты можно резюмировать следующим образом.

• 1.    При восстановительных микрохирургических операциях на эластичных структурах является принципиальным восстановление нормального, т.е. существовавшего до травмы, их естественно-напряженного состояния.

• 2.    Предложенный способ расчета продольной силы натяжения в растянутых эластичных структурах позволяет выбрать дальнейшую хирургическую тактику, решить вопрос о целесообразности использования трансплантатов и определить их длину.

• 3.    Дифференцированный подход к выбору оптимальной длины трансплантата в зависимости от биомеханических свойств восстанавливаемых структур значительно улучшает результаты аутотендо- и аутоневральной пластики.

• 4.    Внедрение элементов программного обеспечения в сопровождение хирургической операции при восстановлении поврежденных эластичных структур позволило оптимизировать алгоритм их восстановления.

• 5.    Первичное восстановление поврежденных эластичных структур, при наличии соответствующих условий, и обязательная последующая комплексная индивидуальная реабилитация пациента позволяют значительно улучшить ближайшие и отдаленные результаты лечения.

24 с.