О некоторых методических аспектах исследования индивидуальности человека

В отечественной психологии существует несколько подходов к изучению индивидуальности человека (Ананьев, 2001; Мерлин, 1986; Русалов, 2012). Несмотря на некоторые разногласия, порой достаточно серьезные, эти подходы схожи тем, что предлагают изучать человека целостно, начиная с его биологических основ и заканчивая высшими социальными и духовными проявлениями. В послед- ние десятилетия к проблеме всестороннего изучения индивидуальности человека обращаются идеологи теории черт, понимая важность учета как биологических, так и социальных детерминант личности (McAdams, 2006; McCrae, Costa, 2008).

Операционализация любой разработанной оригинальной теории – одна из важнейших задач, стоящих перед ее создателем, его учени- ками и последователями. Поэтому все психологические школы, в той или иной мере занимающиеся разработкой новых теоретических построений (в том числе и научные сообщества, изучающие феномен индивидуальности), широко используют математический аппарат. Любая попытка изучения человека целостно требует включения в системный анализ множества переменных, отражающих разные стороны и уровни индивидуальности. Одним из аспектов такого отражения является выявление взаимного влияния переменных. В рамках такой парадигмы главными методами изучения многочисленных взаимосвязей становятся корреляционный и факторный анализы. Однако при сборе статистических данных и их обработке важно соблюдать ряд требований, игнорирование или нарушение которых может привести в последующем к серьезным искажениям. Существует множество пособий и статей, в которых указаны допущения применимости тех или иных статистических процедур, включая корреляционный и факторный анализы (Гржибовский, 2017; Наследов, 2008).

В настоящей публикации приводится упоминание лишь на некоторые из них, а также освещаются редко обсуждаемые проблемы применения корреляционного дизайна, рассматриваемые в контексте изучения индивидуальности.

Проблема нелинейных зависимостей. Не всегда связь между двумя свойствами характеризуется линейностью (формулировочно точнее – линейной зависимостью, чаще в понимании – прямой линейной зависимостью)¹. Поскольку при разработке многих дизайнов исследования (и исследованиях индивидуальности) часто используются корреляционные дизайны, поэтому важно учитывать возможную нелинейность, чтобы не упустить значимые взаимосвязи (Калугин, 2018а, 2018б).

Более того, некоторые связи могут быть ошибочно приняты за несущественные, когда их характер изменился с линейного на нелинейный! Рассмотрим два примера. На рис. 1a представлена положительная прямолинейная зависимость, которая хорошо описывается с помощью r Пирсона (r = 0,94, p < 0,001) или ρ Спирмена (ρ = 0,95, p < 0,001). Однако при наличии нелинейной зависимости, например, гиперболической (рис. 1b) или параболической

(рис. 1c), корреляционный анализ как по Пирсону, так и Спирмену, не улавливая закономерности, занижает значение при гиперболическом варианте: r = –0,57, p < 0,001 и ρ = –0,55; p < 0,001 соответственно. В случае параболической зависимости эта тенденция становится еще очевиднее: r = –0,01; p = 0,822 и ρ = 0,001; p = 0,980 соответственно. Однако в ряде случаев зависимости при нелинейной связи лучше выявляются с помощью непараметрических критериев Спирмена и Кендалла, чем с помощью критерия Пирсона (Шитиков, Розенберг, 2013, с. 87).

Традиционными способами обнаружения нелинейной связи между переменными являются определение «индекса корреляции» и «корреляционного отношения» (Ферстер, Ренц, 1983). Нелинейные модели широко используются при регрессионном анализе, машинном обучении. Однако в случае с корреляционным анализом нелинейность крайне ограниченно является предметом отдельного исследования и, скорее, она рассматривается в контексте проверки допущения применимости процедур линейного корреляционного анализа.

Относительно недавно появились новые способы исследования нелинейности с помощью «частных моментов» (Viole, Nawrocki, 2012), реализованные в пакете «NNS» в среде R²; с определением т. н. максимального информационного коэффициента (maximal information coefficient, MIC) (Reshef et al., 2011), реализованного в пакете «minerva»; методом корреляции дистанций (distance correlation) (Szekely et al., 2007), реализованной в пакете «energy», и др. Наилучшие результаты, согласно результатам сравнения нескольких вариантов нелинейных корреляций (Deebani, Kachouie, 2018), демонстрирует максимальная корреляция (maximal correlation), реализованная в пакете «acepack» (Breiman, Friedman, 1985). Наличие нескольких групп в данных . В целом к статистическому анализу следует подходить с особой тщательностью, так как в рамках корреляционного дизайна можно совершить ошибку, ориентируясь только на

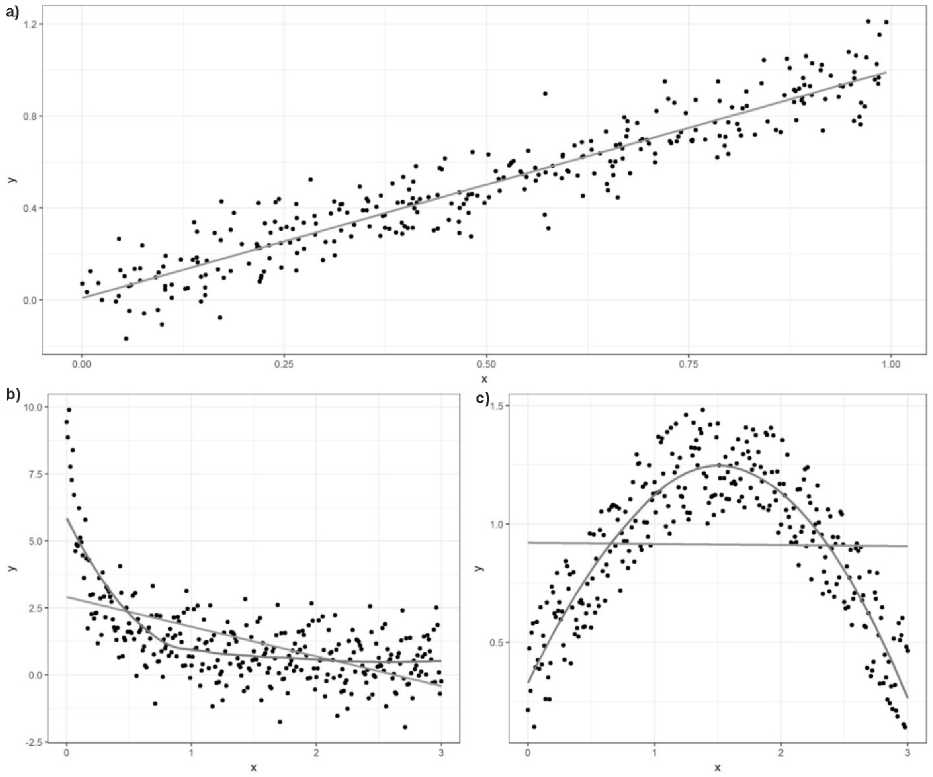
Рис. 1. Линейная (a), нелинейная гиперболическая (b) и параболическая (c) взаимосвязь: прямая линяя – линия регрессии, отражающая линейную зависимость, кривая линия – линия регрессии, отражающая реальную зависимость в данных

Fig. 1. Rectilinear (a), nonlinear hyperbolic (b) and parabolic (c) relation: straight line – regression line, reflecting linear dependence, curved line – regression line, reflecting the real dependence in the data

значение коэффициента корреляции. На рис. 2 представлена взаимосвязь ширины чашелистика и длины лепестка из классических данных Р. Фишера «Ирисы». Корреляционный анализ Пирсона обнаруживает значимую отрицательную взаимосвязь между данными (r = –0,43; p < 0,001), при этом при визуальном изучении диаграммы рассеяния в данных можно наблюдать явное присутствие двух групп. Корреляция по Пирсону, проведенная отдельно для каждой группы, дает следующие результаты:

• •    для большего размера группы: r = 0,54; p < 0,001;

• •    для меньшего размера группы: r = 0,13; p = 0,359.

Таким образом, не только значимость корреляции меняется, но она даже меняет знак на противоположный! Известное правило – «визуальное изучение диаграмм рассеяния» – часто не выполняется, и исследователь ориентируется только на табличные значения.

Коррекция корреляции для ограниченного диапазона . Также приведем пример проблемы, возникающей в случае разбиения результатов на три группы (высокие, средние, низкие) по какому-либо признаку, с дальнейшим включением такого признака в анализ (данные взяты из исследования (Калугин, 2015)). На рис. 3 представлена диаграмма рассеяния, демонстрирующая взаимосвязь между «эмоциональной реактивностью» и «выносливостью», измеренными по методике FCB-TI Я. Стреляу. Общая выборка респондентов составила 287 человек. Далее с помощью кластерного анализа методом k-средних выборка

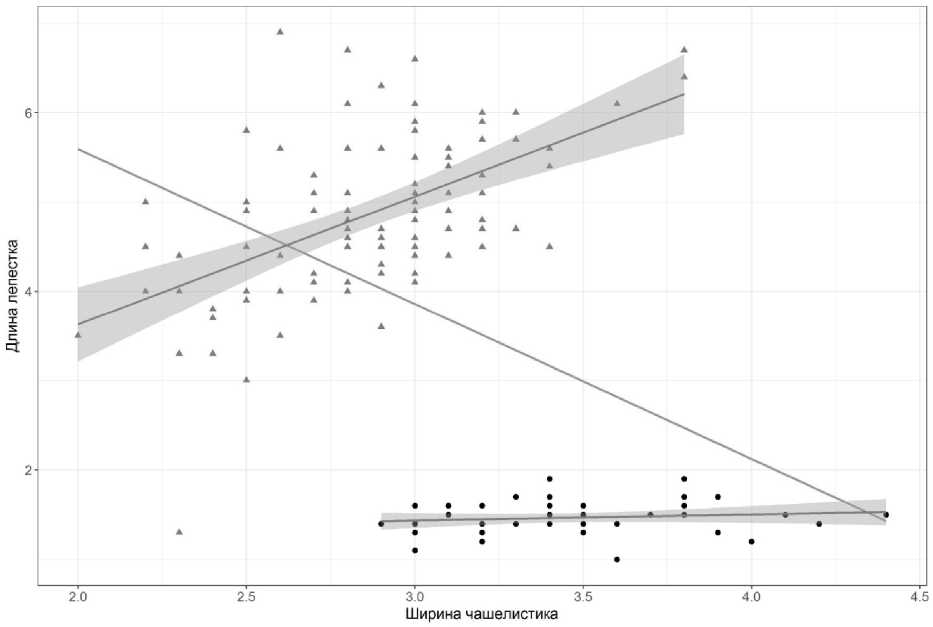
Рис. 2. Проблема наличия групп в исследуемых данных: треугольниками и точками изображены группы наблюдений, прямая линия – линия регрессии для анализа, проведенного на всей совокупности данных, прямые линии со шлейфом – линии регрессии для каждой совокупности отдельно, серый шлейф – 95 % доверительные интервалы

Fig. 2. The problem of the presence of groups in the studied data: the triangles and dots represent the groups of observations, the straight line is the regression line for the analysis performed on the entire data set, the straight lines with the loop are the regression lines for each set separately, the gray loop is 95% confidence intervals

была разделена на группы по критерию уровня значений переменной «эмоциональная реактивность» (ЭР): кластер с низкими показателями по ЭР включал 57 испытуемых, кластер со средними показателями ЭР – 137, кластер с высокими показателями ЭР – 93.

Исходя из анализа представленной на легенде рис. 3 информации, следует подчеркнуть, что линия регрессии в кластерах (подвыборках испытуемых) уже не так явно характеризует отрицательную корреляцию (в отличие от общегрупповых данных). Аргументами этому служат значения коэффициентов корреляции r Пирсона, средних арифметических М и стандартных отклонений SD для указанных групп:

• •    в общей выборке: r = –0,68, p < 0,001; M = 50, SD = 10;

• •    группа с низкими значениями ЭР: r = –0,44; p < 0,001; M = 35,63; SD = 4,86;

• •    группа со средними значениями ЭР: r = –0,28; p = 0,001; M = 48,23; SD = 3,67;

• •    группа с высокими значениями ЭР: r = –0,27; p = 0,008; M = 61,22; SD = 4,14.

C математической позиции такие изменения обосновываются представлениями о корреляции как отношении ковариации к квадратному корню произведения двух дисперсий. Поэтому если дисперсия переменной будет искусственно ограничена (как в рассматриваемом случае), то корреляция будет уменьшена, несмотря на то, что наклон линии регрессии может остаться прежним (Revelle, 2018, с. 120). Следует отметить, что ограничение сразу по двум переменным приведет к еще большим искажениям результатов.

Отметим, что в психометрике разработаны методы коррекции такого искажения коэффициентов корреляции для ограниченного диапазона (correct correlations for restriction of range), также известные как «Thorndike’s Case II» (в наше время существует несколько подходов к коррекции для разных случаев (Tran, 2011)).

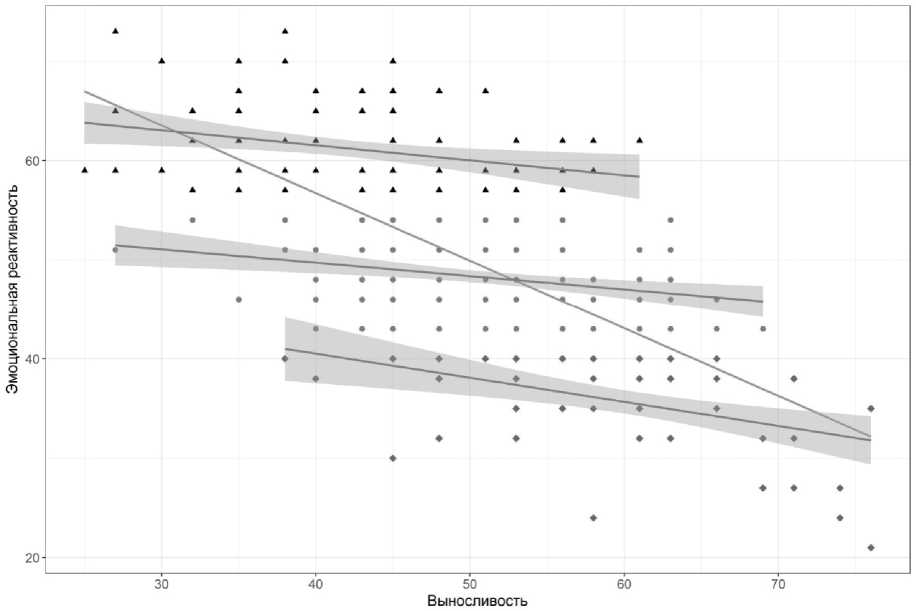
Рис. 3. Проблема ограниченного диапазона в корреляционном анализе: треугольниками, точками и ромбиками изображены выделенные кластеры, прямая линия – линия регрессии для анализа, проведенного на всей совокупности данных, прямые линии со шлейфом – линии регрессии для каждой совокупности отдельно, серый шлейф – 95 % доверительные интервалы

Fig. 3. The problem of limited range in the correlation analysis : the triangles, dots and diamonds represent the selected clusters, the straight line is the regression line for the analysis performed on the entire data set, the straight lines with the loop are the regression lines for each set separately, the gray loop is 95% confidence intervals

В случае с «Thorndike’s Case II» важно, чтобы переменные были линейно связаны. Также не следует включать в анализ статистику, сильно коррелирующую с переменной, на основании которой было произведено де- ление на группы, так как она косвенно тоже подвергается «ограничению диапазона» (Hunter, Schmidt, 2004).

Необходимые функции есть в пакетах «psych», «psychometric» и «selection» в среде R. Однако рассчитать скорректированные коэффициенты можно и «вручную» по следующей формуле (приводится по: Tran, 2011, с. 5):

R =

r*S s

T-^^s2/?

где r – корреляция в ограниченной выборке; S – стандартное отклонение в неограниченной выборке; s – стандартное отклонение в ограниченной выборке.

Таким образом, скорректированные коэффициенты корреляции для рассматриваемых групп на примере рис. 3 следующие:

• •    группа с низкими значениями ЭР: r = –0,71; p < 0,001;

• •    группа со средними значениями ЭР: r = –0,62; p < 0,001;

• •    группа с высокими значениями ЭР: r = –0,56; p < 0,001.

Эти данные уже не столь сильно отличаются от значений корреляции, вычисленной для всей выборки респондентов (r = –0,68, p < 0,001).

Описанный случай не означает, что разделять массивы данных на подвыборки не стоит, но при этом важно учитывать возможные искажения и либо корректировать их, либо не включать в последующий анализ переменную, на основе которой было осуществлено деление на группы, а также сильно коррелирующие с ней переменные.

Уровень значимости и величина эффекта . В ряде случаев при разбиении на группы может наблюдаться исчезновение ранее выявленной значимой корреляции между переменными, что, например, в рамках теории ин тегральной индивидуальности В.С. Мерлина

(1986) может быть проинтерпретировано как разрушение связи между свойствами ввиду формирования индивидуального стиля. Однако исчезновение значимости связи может быть обусловлено иными причинами. Уровень значимости напрямую связан с объемом выборки, поэтому снижение размера выборки из-за разделения ее на подгруппы может привести к «незначимому» коэффициенту корреляции. За это и за некоторые другие проблемные моменты показатель значимости не раз критиковался (Сивуха, Козяк, 2009; Cohen, 1994; Cumming, 2014) в основном сторонниками представлений о большей информативности величины эффекта и интервальных оценок (доверительных интервалов). Об этих подходах и их критике можно подробнее прочитать в ряде публикаций (Сивуха, Козяк, 2009; Корнеев, 2016). Поэтому имеет смысл указывать помимо уровня значимости (желательно точного, а не округленного до одного из трех значений: 0,05; 0,01 и 0,001 – см., например, Publication Manual…, 2010) также доверительные интервалы и значения коэффициента величины эффекта (меры эффекта d) Коэна (или его аналоги) (Tellez et al., 2015). Любая традиционная статистическая величина (t, r, F, χ2 и др.) может быть преобразована в d, например, с использованием соответствующих функций из библиотек «effsize», «psych» и др. в R либо с помощью онлайн-калькуляторов (например, https://www. .

Помимо всего вышеописанного следует помнить, что сравнивание коэффициентов корреляции разных групп «на глазок» неправомерно: например, разница между корреляциями r 1 = 0,5 и r 2 = 0,3 может быть значимой при размерах выборок n 1 = 250 и n 2 = 100 соответственно, однако она будет незначимой при размерах выборок n 1 = 200 и n 2 = 100. Для таких целей существуют специализированные функции в пакете «psych» в R и в пакете Sta-tistica корпорации StatSoft.

Проблема множественных сравнений (multiple comparisons, multiple testing problem). Традиционно при исследовании индивидуальности человека в корреляционном анализе или анализе различий используются десятки переменных, что приводит к опасности переоценить количество значимых связей или значимых различий (в большом объеме данных обязательно обнаружатся значимые взаимосвязи или различия).

Приведем пример частой ошибки: использование t-критерия Стьюдента для случая трех групп вместо применения однофакторного дисперсионного анализа. Исследуются различия по какой-либо переменной в трех группах (A, B и C). Для этого проводится три сравнения с помощью t-критерия: A-B, B-C и A-C. Предположим, что для каждого сравнения обнаружено значимое различие на уровне p < 0,05. Однако вероятность ошибки в этом случае рассчитывается по следующей формуле (приводится по: Bretz et al., 2010, p. 1):

P = i-(i- a ) m , (2) где a - уровень значимости, на который ориентируется исследователь (обычно 0,05);

m – количество тестирований нулевых гипотез;

P – вероятность совершить хотя бы одну ошибку I рода.

Таким образом, для трех сравнений вероятность ошибиться составит: P = 1 – (1 – 0,05)3 = = 0,14 (а вовсе не 0,05, как ожидает исследователь).

До настоящего времени разработано множество поправок для уровня значимости: поправка Бонферрони, поправка Холма, поправка Бенджамини-Хохберга и др. (Bretz et al., 2010). Корректировка уровня значимости на множественную проверку гипотез позволит повысить качество получаемых значимых взаимосвязей или различий, а также повышает уверенность в достоверности научных результатов. В случае использования среды R для получения таких поправок применяются соответствующие функции как базового пакета «stats», так и других пакетов, в том числе специализированных («multcomp» и др.).

Перестановочные тесты и бутстреп. Тестирование гипотез с помощью параметрических методов (t-критерий Стьюдента, корреляционный анализ Пирсона, F-критерий Фишера для однофакторного дисперсионного анализа и т. д.) требует соблюдения целого ряда допущений. Среди основных из них – необходимость обеспечения соответствия эмпирического распределения теоретическому нормальному, чего в конкретных случаях не всегда удается добиться. В случае асимметричного распределения и/или нарушения иных допущений обычно рекомендуют использовать непараметрические аналоги (U-критерий Манна – Уитни, корреляционный анализ Спирмена, H-критерий Краскела – Уоллиса и т. п.). Последние характеризуются меньшей мощностью по сравнению с параметрическими. В последнее время при решении задач исследования все чаще предпочтение отдается т.н. робастным техникам3, которые, с одной стороны, устойчивы к помехам, а с другой – позволяют получить достаточно надежные результаты, в ряде случаев превосходящие по мощности параметрические тесты. К таким относятся, например, перестановочные тесты (permutation tests), которые позволяют получить эмпирическое распределение критерия и на этой основе рассчитать его уровень значимости (Кабаков, 2016; Шитиков, Розенберг, 2013). Как показывают сравнения мощности классических тестов и перестановочных, последние демонстрируют существенно большую мощность (Мелас и др., 2016). В рамках парадигмы рандомизированного подхода широко используется бутстреп4 (bootstrap) и вычисление на его основе 95 % доверительных интервалов. В среде R функции для перестановочных тестов можно найти в пакетах «coin» и «lmPerm», функции для бутстрепа – в пакете «boot».

Проблема воспроизводимости. В последние годы активно обсуждается проблема воспроизводимости психологических исследований (Open Science Collaboration…, 2015). Эта проблема напрямую касается и исследования индивидуальности: зачастую в рамках единой исследовательской программы используются одни и те же методы для изучения разноуровневых свойств индивидуальности. Таким образом, на протяжении десятилетий накапливается богатый эмпирический материал, доступный изучению и сравнению. Однако использование этих данных для проверки вос- производимости и проведения метаанализа сопряжено с существенными трудностями: в связи с отсутствием четких требований к предоставлению материала, к степени его открытости результаты исследований зачастую подаются в усеченном виде (незначимые коэффициенты в корреляционном и низкие нагрузки в факторном анализах не приводятся, многочисленные взаимосвязи визуализируются с помощью корреляционных графов, а величина статистики при этом не указывается и т. п.), описательные статистики часто носят поверхностный характер и т. д.

В мировой науке наметился переход к новой парадигме, требующей «метааналитическо-го мышления», максимально подробного представления полученных в исследовании данных; публикации, в том числе негативных результатов, наличия, в том числе, высокой статистической культуры исследователя (Корнеев и др., 2016; Корнилов, Корнилова, 2010; Корнилова, 2010; Сивуха, Козяк, 2009; Cumming, 2012; Kline, 2013). Вероятно, требуется серьезная организационная и просвещенческая работа, связанная с выработкой четких требований к представлению результатов исследований (прежде всего – статистических) и доведением этих требований до научной общественности.

Выводы

В настоящей публикации были рассмотрены некоторые теоретические и методические проблемы, стоящие перед исследователем феномена индивидуальности человека: учет характера корреляционных связей (линейность – нелинейность, внутренняя структура данных); специфика разбиения на подгруппы; проблема множественных сравнений; робастные и сходные с ними новые статистические процедуры; проблема воспроизводимости. Отдельный важный методический аспект – требование к полноте представления информации, в частности, приведение полных корреляционных таблиц и результатов факторного анализа, приведение точного уровня значимости, величин статистического эффекта и доверительных интервалов. Все это позволит использовать в дальнейшем метаанализ и перейти к новому уровню научного обобщения.

Исследование выполнено за счет гранта Российского научного фонда (проект 18-18-00386), Институт психологии РАН.