О некоторых моделях нанотрибологии

В работах [1–2] развит итерационный метод решения задач наномеханики в квазистатической постановке, основанный на использовании метода Ньютона–Рафсона, и решен ряд одномерных задач для цепочек атомов. В настоящей работе построены численные решения задач об определении сил трения для разных моделей трения: Томлинсона, Френкеля–Конторовой и некоторых обобщений одномерных моделей, связанных с учетом дальнодействия в рамках теории центральных парных взаимодействий. Проведено сравнение решений, отмечены достоинства и недостатки.

В настоящей работе решена задача об определении сил трения в обобщенной модели Томлинсона, в которой изучено влияние сил дальнодействия, описываемых потенциалом Морса, при этом из всех гипотез Томлинсона сохранена гипотеза о постоянстве расстояния между цепочками, что позволило рассматривать только одномерные по координатам задачи. Дано сопоставление предложенной обобщенной модели с моделями Томлинсона и Френкеля–Конторовой, в результате которого сделаны выводы об областях применения упрощенных моделей, а также выявлены некоторые новые механические эффекты.

Задача ставится следующим образом. Рассматривается взаимодействие двух атомных цепочек, одна из которых (основание) движется как жесткое целое вдоль собственной оси. Вторая цепочка, параллельная первой, деформируется под воздействием атомов основания. В исторически первой работе Томлинсона [3]

принималось, что на каждый атом деформируемой цепочки действует сила, равная первому члену разложения поля сил взаимодействия атомов основания и деформируемой цепочки в ряд Фурье; постоянный член разложения полагался равным нулю, что верно только для некоторых частных случаев. Эти гипотезы позволили расщепить систему уравнений равновесия всей системы на совокупность уравнений для отдельных атомов, изучить вопросы существования, единственности и устойчивости, исследовать влияние отношения периодов цепочек. В модели Френкеля–Конторовой [4] построена система связанных друг с другом уравнений, исходя из дополнительной гипотезы о том, что атомы деформируемой цепочки связаны друг с другом линейно-упругими пружинами.

2.    Взаимодействие двух атомных цепочек

Рассматриваются две цепочки атомов, параллельные друг другу, одна из которых является деформируемой, а вторая — абсолютно жесткой (Рис. 1). Атомы деформируемой цепочки занумерованы целыми числами i ( i = 0,1,..., N ), атом «0» неподвижен. Цепочка характеризуется равновесным расстоянием r_e между двумя соседними атомами, а также их начальными координатами r_i ⁰ . Текущее расстояние r_ij между атомами i , j равно r jj = | r 0 + u j - ( r ° + u i )| , где u i , u j — перемещения относительно начального состояния. В справочниках обычно приводятся значения величины r_e для пары изолированных атомов. Если же величина N конечна, то в ненагруженной цепочке происходит уменьшение r_e на некоторую постоянную величину вдали от концов цепочки и на переменную величину в окрестности концов (на расстояниях порядка 3–4 r_e ). Этот эффект изучен в работе [1] и назван эффектом самосжатия.

Атомы деформируемой цепочки перемещаются из их равновесного состояния под действием поля сил, которое порождается движущейся жесткой цепочкой. Расстояние между соседними атомами жесткой цепочки постоянно и равно a = 2^, где п — заданное вещественное число (сила трения между бесконечными цепочками в модели Томлинсона зависит от того, является ли число п целым, рациональным или иррациональным [3]). Вводятся следующие обозначения: U _c — заданное смещение жесткой цепочки; d — расстояние межу цепочками; N _A — количество атомов в жесткой цепочке, которое может быть бесконечно большим.

Жесткая цепочка в начальном состоянии характеризуется сдвигом S ее первого атома относительно начала координат O ; ось Ox координатной системы направлена вдоль первой цепочки, точка O совпадает с первым атомом, для которого i = 0 . Разложение поля сил в ряд Фурье имеет вид:

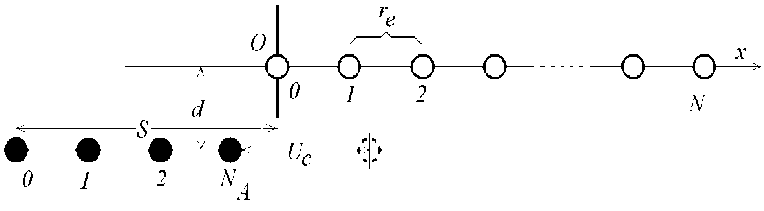
Рис. 1. Расчетная схема

F ( x ) = f 0 + Z f k sin —⁽ x + U c ) a

k

В моделях Томлинсона ( Т) и Френкеля-Конторовой ( FK) полагается, что f 0 = 0 и f_k = 0 для всех к * 1 . В квазистатической задаче, то есть без учета сил инерции, модель Томлинсона сводится к следующей системе уравнений равновесия:

k_Tu_l + f 1 sin[ n ( lr_l + u_l + U_c )/ a ] = 0    ( l = 1, 2,...)

где u_l — перемещение l -го атома; k_T — коэффициент сопротивления среды, которая считается линейно упругой. Каждое из уравнений (2) решается независимо от других; анализ существования, единственности и устойчивости решений приводится в работе [5].

В модели Френкеля–Конторовой используется допущение, что каждый атом связан с соседними атомами линейно упругой пружиной. При сохранении гипотезы Томлинсона относительно внешнего силового поля система уравнений равновесия в FK –модели приобретает вид:

^k FK ⁽ u l - 1 ^{- 2} u l ⁺ u l + 1 ) ^- f 1 ^{sin[ n ( l}r l ⁺ u l ^{+ U} c )/ ^{a ]} = ⁰, (3)

где k_FK — жесткость пружин.

В настоящей работе предлагается обобщение моделей (2) и (3), основанное на использовании гипотезы о парном центральном взаимодействии и на аппроксимации Морса [6] для потенциала силового поля. В результате получается система нелинейных уравнений для перемещений:

Ф(S) = FR - F L - F ext = 0,

N

F R = 2 D ^a £ { exp[ - « ⁽ X p ^- X i ^{- r}e + U p ^- U i ^{)] -} eXp[ - 2 « ⁽ X p ^- X i ^- r e ) + U p ^- U i ^)] } , p = i + 1

i - 1

FL = 2Da ^ {exp[-a(xi - xp - re + ui - up )] - exp[-2a(xi - xp - re ) + ui - up )]}, p=0

N A

Fexz = 2 Da ^{exp[-a( rl - re)] - exp[-2a( rl - re)]}cos Pil, l=0

где F R , F L — силы, действующие на атомы подвижной цепочки справа и слева соответственно; F ext — сила, действующая на атомы деформируемой цепочки со стороны атомов подвижной жесткой цепочки; i = 1, 2,..., N — номер уравнения равновесия атома с номером i; Pil — угол между осью Ox и радиус-вектором r; D, a — постоянные потенциала Морса, который описывает взаимодействие пары атомов данного вещества (постоянные D, а в выражениях (5) и в формуле (6) для Fext могут различаться значениями). Замена в формуле (6) cos Ра на sin Ра позволяет найти величину адгезионного сцепления цепочек атомов.

Система (4) решается методом Ньютона–Рафсона, подробно описанным в работе [1].

3.    Численные результаты

Ниже приводятся численные результаты для цепочек из атомов алюминия. Значения постоянных D , а взяты из работы [6]. Использованы следующие исходные данные: N = 20; N A = 10 (для всех приведенных ниже результатов, за исключением тех, которые иллюстрируют разрушение деформируемой цепочки); a = r e ; максимальное значение смещения U c = U ™^x = 30 r e ; f 1 = 0,1; k T = k_FK = 1; S = - 10 r e . Число шагов по нагрузке составляло N _Ooad = 400, величина шага по нагрузке — h = U_c ^max / N _Oaid , число итераций на шаге в методе Ньютона–Рафсона — 100.

На рисунке 2 показаны силы трения F , определяемые как сумма Ox -компонент вектора F ^ext ; по горизонтальной оси отложено K — количество жестких смещений U c . Силы F подсчитывались для атома с номером i = N /2 (кривая 2), кроме сил, соответствующих кривой 1, которые находились для значения i = 0 . Кривая 2, получаемая жестким сдвигом кривой 1, показывает изменение сил трения, определяемых как сумма сил, действующих на атом с номером i = N /2 . Этот результат использовался в дальнейшем как один из критериев правильности работы программы. Видно, что силы трения имеют два максимума, соответствующих случаю совпадения координаты крайнего правого атома подвижной жесткой цепочки со средним атомом деформируемой цепочки (сила действует влево) и случаю совпадения координаты крайнего левого атома подвижной жесткой цепочки со средним атомом деформируемой цепочки (сила действует вправо). Кроме того, ввиду быстрого затухания сил межатомного взаимодействия, существуют две области с нулевыми силами трения (слева и справа от максимумов). Третья , средняя область почти нулевых сил трения, возникает вследствие разных направлений проекций на ось Ox сил взаимодействия атомов при достаточном удалении атомов жесткой цепочки от концов деформируемой цепочки. Кривая 3 показывает поведение сил трения, предсказываемое моделями Томлинсона и Френкеля– Конторовой. Эта кривая имеет колебательный характер; совпадение решений по теориям Томлинсона и Френкеля-Конторовой объясняется совпадением жесткостей k_T = k_FK = 1. Кривая 4 иллюстрирует зависимость сил адгезии от изменения U_c .

Следует отметить, что в действительности решение по обобщенной модели также имеет колебательный характер. Это демонстрирует рисунок 3, на котором представлен фрагмент средней части кривой 2 с рисунка 2 (точечная линия) и его укрупненное изображение (сплошная линия). Следовательно, гипотеза Томлинсона может использоваться только в ограниченном диапазоне изменения параметра U_c при надлежащем подборе амплитуды f ₁ в системе уравнений (2). Это утверждение справедливо, естественно, в рамках исследуемой постановки задачи.

На рисунке 4 показано распределение сил P , действующих справа на все атомы деформируемой цепочки ( i = 0, 1, 2, ..., N ) в ее конечном состоянии для трех моделей трения: сплошная кривая соответствует обобщенной модели, штриховая — моделям Томлинсона и Френкеля-Конторовой при f ₀ = 0 , точечная — последним двум моделям при f 0 = 3,636. Это значение соответствует средней части сплошной кривой; оно получено численно в рамках обобщенной модели. Таким образом, классические модели Томлинсона и Френкеля–Конторовой хорошо работают в области, удаленной от пограничных слоев атомов.

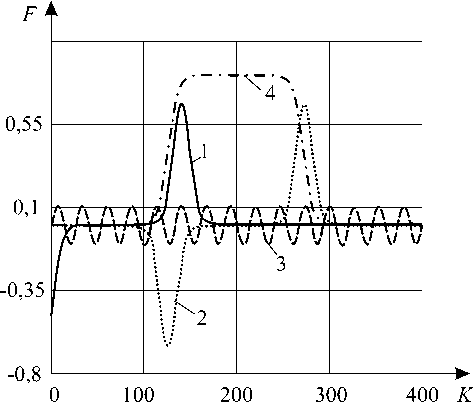
Рис. 2. Зависимость сил адгезии (кривая 1) и трения от внешних воздействий ( обобщенная модель: 2 – i = 0; 3 - — i = N/ 2; 4 - модели Томлинсона и

Френкеля–Конторовой)

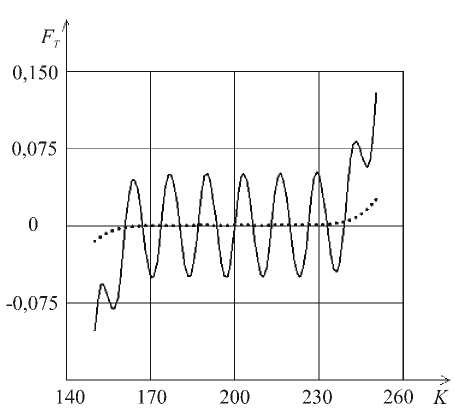
Рис. 3. Распределение сил трения в средней части шкалы K (точечная кривая соответствует масштабу сил F рисунка 2)

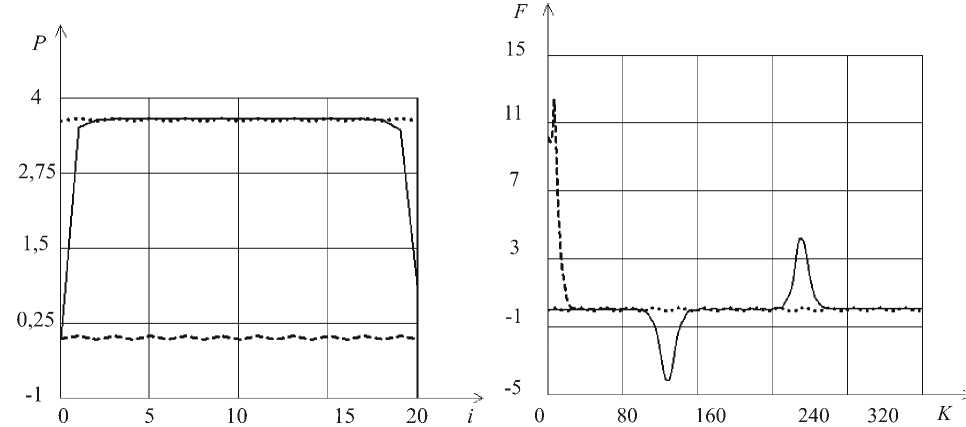
Рис. 4. Силы взаимодействия между атомами

Рис. 5. Силы трения при разрушении

Рисунок 5 демонстрирует возможности алгоритма в описании процесса разрушения деформируемой цепочки. Штриховая кривая соответствует решению по обобщенной модели при следующих значениях параметров: d = 1 , S = 10 , U c = U™ = 10 r e . Сильная связь при d = 1 жесткой и деформируемой цепочек приводит к тому, что в промежутке от 6-го до 25-го шага происходит уменьшение силы трения примерно на два порядка — от 12,169 до 0,107 единиц силы в системе измерения, предложенной в [6], то есть происходит разрушение цепочки. Сплошная кривая изображает процесс без разрушения для d = 3,0 , точечная — решение по моделям Томлинсона и Френкеля-Конторовой.

Поведение цепочки после разрушения иллюстрируется ломаной линией 1 на рисунке 6, характеризующей распределение перемещений по цепочке в конечном ее состоянии, то есть при U c = U^ = 10 r e . Видно, что разрушение представляет собой

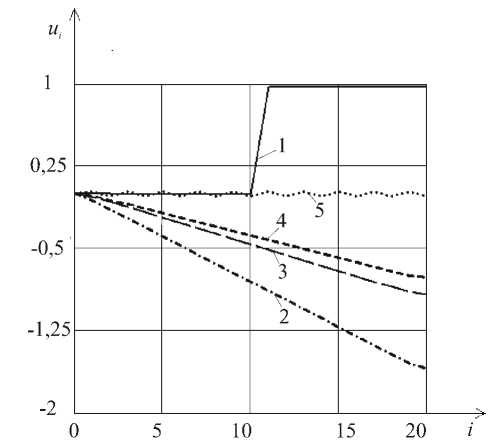
Рис. 6. Распределение перемещений атомов отрыв среднего (11-го) атома от 10-го, то есть цепочка разрушается точно посередине, после чего оторвавшаяся часть движется вместе с жесткой цепочкой. Остальные кривые соответствуют процессам нагружения цепочки без разрушения: 2 — d = 1,5 ; 3 — d = 2,0; 4 — d = 3,0 ; 5 — модели Томлинсона и Френкеля–Конторовой.

4.    Заключение

В работе предложена новая модель трения на наноуровне, представляющая собой обобщение классических моделей Томлинсона и Френкеля–Конторовой на случай учета дальнодействия в рамках теории центральных парных взаимодействий. Построены численные решения задач об определении сил трения, распределений сил и перемещений в деформируемой цепочке для разных моделей трения: Томлинсона, Френкеля– Конторовой и предложенной в работе обобщенной одномерной модели. Проведено сравнение решений, выявлены некоторые важные механические эффекты и указаны области применимости классических моделей.

Работа выполнена при частичной финансовой поддержке грантов Российского фонда фундаментальных исследований (проекты № 08-01-00349 и № 07-06-00269).